Smart Grid and Renewable Energy
Vol.06 No.06(2015), Article ID:57282,15 pages
10.4236/sgre.2015.66014
Power Quality Issues Concerning Photovoltaic Generation in Distribution Grids
Jaan Niitsoo1, Marek Jarkovoi2, Paul Taklaja1, Joni Klüss3, Ivo Palu1
1Department of Electrical Power Engineering, Tallinn University of Technology, Tallinn, Estonia
2Department of Electrical Engineering, Tallinn University of Technology, Tallinn, Estonia
3Department of Electrical Engineering and Automation, Aalto University, Helsinki, Finland
Email: jaan.niitsoo@ttu.ee
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 May 2015; accepted 16 June 2015; published 19 June 2015
ABSTRACT
Unregulated utilization of renewable generation including residential photovoltaic (PV) systems can have a significant impact on load characteristics in distribution networks. For improving PV generation capabilities, power quality aspects have to be coordinated with present load characteristics. This paper discusses the harmonic content of PV generation and the influence to power quality indicators in residential distribution networks. PV generation measurement results including current harmonic amplitude and phase angle values are presented. Results of different modelling scenarios are analysed and a simplified model of harmonics in PVs is offered. The results of the study showed a moderate additional harmonic distortion in residential load current and voltage distortion at the substation’s busbar when PVs were added. Novelty of the paper is that harmonic current values at higher orders are presented and analysed. The results pointed out in this paper could be further used for modelling the actual harmonic loads of the PVs in distribution networks.
Keywords:
Current Measurement, Load Modelling, Photo Voltaic, Power Quality, Power System Harmonics

1. Introduction
Harmonic voltage levels in low-voltage networks represent an important aspect of power quality. From the point of view of electromagnetic compatibility, they must be kept within the compatibility levels to enable satisfactory operation of all the equipment supplied by the network. Furthermore, since electricity is also defined as a product, utility companies could be held responsible for excessively high harmonic levels and any resulting damage to customers’ property [1] . As such, in Europe, the harmonic voltage limits specified in EN 50160 standard should be met.
Distorted voltage and current in the distribution system may result in undesirable effects, such as overloading, over-voltages, mechanical stress, malfunction of critical control and protection equipment, and lower the efficiency of appliances. Distortion affects all customers fed through the point of common coupling (PCC).
The development of electronics for the general public as well as industrial applications has led to a rapid increase in the number of non-linear loads. In addition to the increased number of electronic devices, also resistive devices such as incandescent lamps are ever more frequently replaced by energy saving lamps utilizing non- linear elements. For example, depending on type and brand, switching power supplies absorb distorted currents which flow through the impedances of the power distribution system and result in distortion of system bus voltage [2] . Harmonics can travel upwards within the network and affect the grid voltage waveform, which may become notably distorted, deviating extensively from a proper sinusoidal signal.
Residential photovoltaic (PV) generators are the dominant renewable energy source in urban and metropolitan areas. This technology is enjoying rapid growth due to a combination of subsidies, the abundance of sunshine, and the low impact of the technology on the urban landscape [3] . As photovoltaic systems incorporate power converters, which are harmonic generating devices, they will have an influence on the power quality of the supply network. High harmonic distortion levels have also been observed in certain remote regions such as winter sports resorts and rural areas far away from substations.
Distributed generation (DG) impacts the network. This impact is dependent on the location, characteristics of the distributed energy source, related power electronic device, network configurations, voltage level at the connection point, and the capacity of DG relative to load consumption [3] . Consequently, utilities are faced with the risk that the permissible levels defined in standard EN 50160 will be exceeded in a significant number of networks in the future [1] . It has been estimated that already in 2012, 60% of the power system loads in USA were nonlinear loads [4] .
Over the past decade, power quality (PQ) issues have become increasingly important in the distribution grid with the widespread use of non-linear electronic equipment. The most cited PQ problems that may arise due to grid connected PV generation are voltage dips and fluctuations, harmonic distortion, transient phenomena and reverse power flow. These effects result in potential damaging of sensitive electronic equipment and capacitor banks, overheating of transformers and neutral conductors and additional losses in the power system. Degraded power quality entails additional costs for both the electricity distributor and its customers [3] [5] .
The purpose of the present study is to demonstrate and analyse possible power quality situations in a residential distribution network by examining the impact of nonlinear domestic loads and PV inverters. For the analysis, measured power consumption and current waveforms of different home appliances and PV inverters have been used. Novelty is that magnitudes and phase angles of each harmonic up to the 50th order were applied for all modelled loads. The main purpose of this paper is to present the use of actual measurement data from different devices for modelling the effects on the residential distribution network and give an estimation of the important values for further modelling.
2. Theory
In electrical power networks, a distorted sine wave can be divided into numerous components, each having an integer-multiple frequency of the main frequency. Different waveforms have different harmonic content referring to individual harmonic magnitudes and phase shift relative to the main frequency component. Hereafter in this paper, the presented measurements of loads are all indicated as magnitudes and phase shift of each individual harmonic up to the 50th order.
Distortions can be observed individually by comparing different harmonic components and calculating harmonic distortion (HD). A more general approach to quantifying the distortions is using the total harmonic distortion level (THD). Total harmonic distortion can be expressed separately for current harmonic distortion as THDI and for voltage distortion as THDU. The harmonic distortion indicators can be calculated using corresponding Equations (1), (2), (3) and (4),
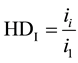 (1)
(1)
 (2)
(2)
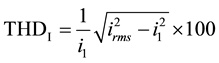 (3)
(3)
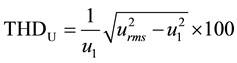 (4)
(4)
where ii is current of order i, i1 is current of 1st order, ui is voltage of order i and u1 is voltage of 1st order.
It has to be pointed out that THDI (total harmonic distortion of current) does not reveal the magnitudes of individual harmonics, which could still exceed the limits for specific harmonics regardless of THDI value. For the correct estimation of the harmonic levels, phase angle values of individual harmonics are also required in addition to magnitudes. It is reported that 10% smaller harmonic current magnitudes can be seen when phase angle information is included compared to the simple summing of magnitudes without phase angle values [6] .
Harmonic currents in a network largely depend on the harmonic characteristics of the connected devices, their phase angles and the background distortion level of the supply voltage. Harmonic current emission spectrum information of a device (or a group of devices connected at a PCC) under different supply voltage conditions is very useful for analysing the device’s influence in the network. This can be further utilised to determine the probability density profile of each order harmonic currents in the network considering their “time-varying” behaviour [7] .
Some loads draw current with total harmonic distortion over 100%, but their active power consumption is not as significant when compared to other harmonic generating devices [8] . In such cases, harmonic distortion may increase significantly when numerous harmonic emitting devices are utilized in bulk. The total impact depends on the number of appliances, their power ratings, and their harmonic diversity. Harmonic angle diversity is also relevant when multiple appliances are operating simultaneously, creating either emergence or cancellation of harmonics [4] . The attenuation effect is dependent only on the phase angle, but the effect’s severity is dependent on the magnitude of the harmonic voltage [9] .
The harmonic generation of a PV system depends on the inverter technology, solar irradiance, temperature, loads, and the supply system characteristics. The harmonic distortion generated in PV plants can occur as a result of intrinsic and extrinsic effects. Intrinsic harmonic distortions are related to inverter deficiencies, e.g. com- ponents and control loop nonlinearities, measurement inaccuracies, and limited pulse-width modulation (PWM) resolution. Connection to a weak and distorted electrical grid can be considered an extrinsic effect on the output waveform of a PV plant. A distorted voltage acts like a disturbance in the inverter control system, causing distortion of the current waveform generated by the inverter [10] .
Several factors affect the power quality characteristics of the PV inverter output current. Both the current THD and the output reactive power are related to the output active power levels, which in turn are strongly dependent on solar irradiance levels. Most of the inverters consume or feed reactive power into the network depending on their output active power and their technology. During operation at low solar irradiance levels (e.g. sunrise, sunset, cloudy days), current THD values can increase rapidly, since the THD factor is inversely proportional to the output active power of the PV inverters. Nevertheless, THD is notably reduced as the output active power of the PV Inverters increases and reaches its nominal value. The intrinsic characteristics of the control circuit and nonlinear components of PV inverters may explain the current distortion behaviour in the low power generation stages [10] [11] .
Varying power density of renewable energy resources (i.e. irradiance level and temperature in PV conversion) potentially cause voltage and frequency variation or sag/swell patterns in the grid. Also, application of power converters as interfaces between energy sources and the grid and their interaction with other system components may cause high harmonics distortion [12] .
In small and distributed or decentralized PV controlled systems, the CSIs (current source inverters) can generate highly distorted current waveforms so that their cumulative effect in high penetration PV systems can create hot spots within transformers; ultimately generating excessive eddy or copper loss [13] .
The differing influences of harmonics in distribution networks are not necessarily visible/evident initially. However, harmonics can have serious long-term consequences, of which the most important ones are [14] :
Overloading of consumer’s electrical installations and power system elements by higher order frequencies of currents and voltages;
Increased heating of neutral conductors caused by triple current harmonics (frequency multiplier of number 3). The increased level of the triple harmonics in the neutral conductor can cause serious damage and even lead to fires because the neutral conductor is not usually overload protected;
Increased transformer heating caused by higher (order and magnitude) harmonics, as well as saturation effects in the core;
Higher harmonics the power system can cause interference to telecommunication lines;
Overstressing and resonant condition on the capacitors bank.
3. Methods
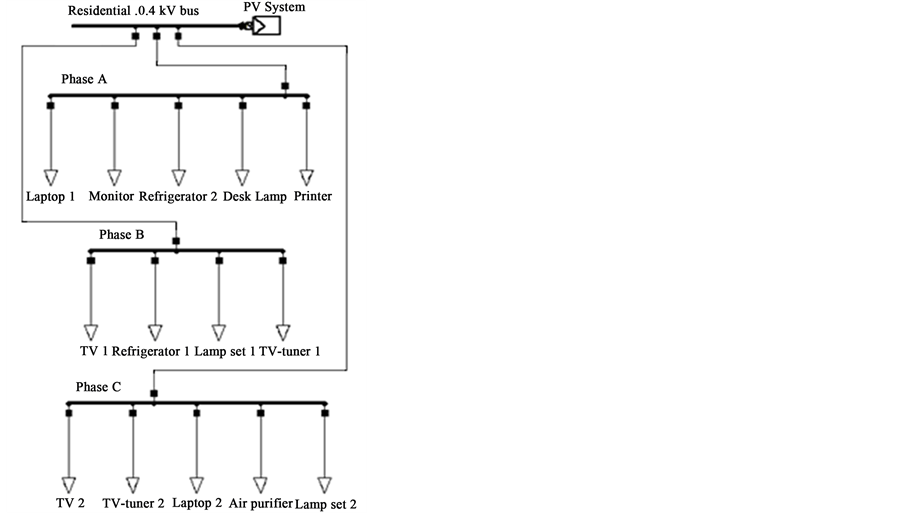
The residential distribution network and loads for assessing load flow were modelled using DIgSILENT Power Factory software. The model consisted of a three-phase residential load at 0.4 kV voltage level composed of different single phase loads. The schematic of the residential load model is presented in Figure 1.
The compiled residential load was connected to the distribution network substation via a 1.4 km long overhead line (OHL) as depicted on Figure 2. The distribution network substation was connected to a 10 kV network with short-circuit power of 200 MVA and short-circuit current 11.5 kA. The high voltage (HV) busbar is modelled as a slack bus. The transformer used in the distribution substation was modelled with the following parameters:
Figure 1. Schematic of residential load model.
Figure 2. Schematic of distribution grid model.
nominal power 25 kVA;
relative short circuit voltage 4.5%;
magnetizing impedance/ short circuit impedance ratio 3;
vector group Yyn.
Implemented parameters in the simulation were selected based on power quality problematic issues identified in Elektrilevi’s network (Estonia’s main distribution grid operator) for July 1, 2013. The length of the OHL between substation and customer’s PCC was defined as an average of all the lines between substations and customers with power quality problems. Similarly, the selected diameter of the line and nominal power of the transformer are the most common values for the identified problematic components.
Harmonic voltage amplitudes and phase angles up to the 50th order were obtained from measurements conducted by Elektrilevi at one of the sites where power quality issues were identified. Harmonic voltage distortion at the 10 kV bus was measured and modelled around 2%, which is a common value for this grid.
For modelling PV generation, three different commercially available PVs were measured for one week. The first measured system was single phase while the remaining were three phase systems. For all three systems, harmonic current amplitudes and angles up to 50th order were measured and used in the models in DIgSILENT. A mean load model of averaged values was composed for the single phase system and it was compared with other models composed of actual measurement results. PV inverters were connected to residential load’s busbar as was described in Figure 1.
In order to model the network response of nonlinear loads, 14 different home appliances were measured. The results of the corresponding measured active and reactive power, harmonic current magnitudes and harmonic current phase shift angles of measured devices are presented in [15] [16] . Modelled devices were arranged in a manner where similar active power consumption was seen in every phase. The model is presumed to be the worst case scenario where all the nonlinear devices are in operation and coincidence factors are not taken into account.
4. Results
First, modelling results are given for the case where one single phase PV system was integrated to the existing grid. In the second and third case, different three phase systems were installed. All three scenarios were examined at three different power levels (stage 1―near 30%, stage 2―near 60%, stage 3―near 100%). Exact power level ratios depended on the availability of measurement data. Initial values of voltage THD in the grid before adding PV generations are presented in Table 1.
1) First case―single phase PV
A single phase PV inverter is connected to the residential busbar at phase C. Measurement results for the three different power levels are given at Table 2 and Table 3. From the tables, it is apparent that current distortion decreases with increasing current. The same conclusion can be made by observing the power factor (PF) value which approaches unity with increasing current. Interestingly in this case, reactive power Q appears to be independent of the current level and changes polarity. In the paper the PF is the real power factor which accounts all values up to 50th order, the cos(fi) stands for displacement power factor which accounts only the main frequency components.
Table 1. Initial modelled voltage THD values [%].
Table 2. Measured power values for single phase PV inverter.
Table 3. Measured power quality values for single phase PV inverter.
Voltage and current distortion during a 15 h period is shown in Figure 3. Voltage distortion at the measurement point was notably low (around 1%) throughout the observed time period and similarly, current distortions are not greatly affected by grid disturbances.
Active power P, reactive power Q, and apparent power S are displayed in Figure 4. Results are in line with the prior conclusion for reactive power where Q is mainly capacitive throughout the measurement period. It can also be confirmed that reactive power is independent of current (compare with P and S).
As is evident in Figure 5, cos(φ) remained near unity throughout the measurement period, whereas PF varied considerably. The observed fluctuations in PF are a result of current distortion which is evident when comparing the current THD and PF curves in Figure 3 (THD_I) and Figure 5 (PF).
Table 4 presents the harmonic currents and phase angles up to the 21st order for the single phase PV inverter with the corresponding power levels described in Table 4. Phase angles are as percentages of main order current angle which is taken zero, main order current are taken 100%. Average values are also calculated and presented for modelling mean one phase PV. Even and higher order harmonics are left out due to their marginal dimension. All presented harmonic current amplitudes exhibited relatively moderate values, except for the third harmonic which was more notable.
For modelling mean PV generation, average values of the presented current harmonic amplitudes and angles (Table 4) were calculated. Main frequency current phase angles were defined zero as in ideal case and other angles were calculated in relation to mains current. Figure 6 shows a graphical representation of the calculated average harmonics, where X and Y coordinates are calculated using Formulas (5) and (6). As it can be seen that the most notable component of the current is 3rd order harmonic.
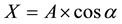 (5)
(5)
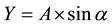 (6)
(6)
In the case where one single phase PV was added to the grid, voltage THD was observed to increase in all phases. Voltage distortion increased more as PV power level increased. Voltage THD for all power output stages and modelled mean PV are presented in Table 5. All values are given in percentages relative to initial conditions prior to the installation of PVs.
2) Second case―first three phase PV
In this case, a three phase PV inverter is connected to the existing network. Measurement results for three different power levels are given in Table 6. Once again, current distortion decreases when current (power) is increasing and same conclusion can be made observing the power factor (PF) value which approaches unity with increasing current. However, diverging from the first case, here total reactive power generation (Q_tot) is growing when current is increasing.
Table 7 provides reactive power and PF values for each phase. In addition to the aforementioned increase in total reactive power, observed reactive power changes were diverse for different phases. It is most probably due to different nature of specific phase load.
Harmonic currents up to 21st order of first three phase PV inverter are given in Table 8 at the different power levels described in Table 2. In this case, the most notable harmonic was the 9th which exhibited values in the proximity of 2% in all phases, even at highest power level. Also the 13th harmonic had prominent values in phases B and C at highest power level. At the lower power level, most of the harmonics had significantly high values, even exceeding 6% at times.
Phase angles of harmonic current amplitudes displayed in Table 8 are given in Table 9. It was observed that angles change with changing currents and as such, no mean values could be presented for this three phase PV inverter.
Voltage and current distortion of the first three phase PV inverter over a 15 hour period is shown in Figure 7.
Figure 3. Measured voltage THD and current THD of single phase PV inverter.
Figure 4. Measured power values of single phase PV inverter.
Figure 5. Measured power factors of single phase PV inverter.
Table 4. Harmonic currents [%] and phase angles [˚] of single phase PV inverter.
Figure 6. Mean harmonic current values of single phase PV inverter.
Figure 7. Measured voltage and current THD values of first three phase PV inverter.
Table 5. Measured power values for single phase PV inverter.
Table 6. Measured values for first three phase PV inverter.
Table 7. Measured Q and PF values of first three phase PV inverter.
Table 8. Measured harmonic currents [%] of first three phase PV inverter.
Table 9. Measured phase angles [˚] of harmonic currents of first three phase PV inverter.
Voltage distortion at the measurement point remained at a moderate level (around 2.25%) throughout most of the time period. Correlation with current distortion was not detected.
Reactive power generation is shown in Figure 8. The figure shows that while reactive power is phases A and B was moderately consumed, reactive power was generated in phase C at a much higher level.
Power indices over the 15 hour period are presented in Figure 9. The figure supports the previous conclusion that reactive power (Q_tot) is mainly inductive. It also confirms that reactive power is independent of current in this case (compare with active power P_tot and apparent power S_tot).
Figure 10 shows that cos(φ) was near unity for the entire duration, whereas PF varied more. PF in phase C was especially poor. Changes in the PF were attributed to current distortion which could be seen when comparing current THD and PF (THD_I in Figure 7 and corresponding PF in Figure 10).
Results of having the first three phase PV in the grid are presented in Table 10. For this case, results are not uniform and voltage THD did not increase in all the stages. Slight harmonic cancellation in phases A and C could be noticed at stage 2. In other stages voltage distortion increased moderately. All values are given in percentages compared to the initial conditions where no PVs were installed.
Figure 8. Measured reactive power values of first three phase PV inverter.
Figure 9. Measured power values of first three phase PV inverter.
Table 10. Voltage THD of grid with PV compared to grid without PV [%].
Figure 10. Measured power factor values of first three phase PV inverter.
3) Third case―second three phase PV
In this case, the three phase PV inverter is replaced with another inverter. Measurement results for three different power levels are given at Table 11. As evident from the table, current distortion decreases with increasing current and similarly, the power factor (PF) value approached unity. Only total reactive power (Q_tot) did not exhibit a linear change.
Reactive power and PF values for each phase are given in Table 12. In addition to the aforementioned total reactive power nonlinearity, reactive power changes were observed to differ for different phases also.
Table 13 presents harmonic currents up to 21st order of second three phase PV inverter at different power levels as described in Table 11. In this case harmonics were notable only at lower power levels. For the first stage, high amplitudes were seen in majority of the presented orders.
Phase angles presented harmonic current amplitudes in Table 13 are displayed in Table 14. Angles were observed to change with changing currents and as such, no mean values could be presented for this three phase PV inverter.
Voltage and current distortion of second three phase PV inverter throughout the 15 h time period is shown in Figure 11. Voltage distortion at the measurement point was mainly low level (around 1.1%). Correlation between voltage and current distortion was not detected.
Reactive power generation is shown in Figure 12. Reactive power in phases A was maintained near zero, while reactive power in the other phases changed frequently in both magnitude and polarity.
Power (P, Q, and S) during the investigated time period is shown in Figure 13 and supports the earlier observation that total reactive power oscillated around zero. A slight correlation with current could be observed in the middle of the day (compare fluctuation in Q_tot with active power P_tot and apparent power S_tot around 14:00).
Figure 14 displays how cos(φ) was maintained near unity majority of the day. Similarly, PF remained rather constant with only minor deviations. The PF curves reached unity with a slight delay and started diminish earlier. The small variation in the middle of the day was in correlation with the rise in total reactive power shown in Figure 13 (Q_tot at 14:00).
The impact of the second three phase PV is presented in Table 15. Results are not uniform and voltage THD did not increased in all the cases. Higher harmonic cancellation could be noticed compared to the previous case with the first three phase PV. A definite assessment concerning distortion changes cannot be done. All values are given in percentages compared to initial conditions where no PVs were installed.
4) Comparison of results
It could be concluded that changes in voltage THD values increase as power output of PVs grows. For the one phase PV installation, it was clear that voltage harmonics increased in all three phases. For the three phase PV installations, the two cases showed different outcomes. With the first three phase PV, notable degradation was observed. However, a conclusive assessment could not be done with second three phase PV installation. Voltage THD results at the highest power level for all three cases are depicted in Figure 15.
Figure 11. Measured voltage and current THD values of second three phase PV inverter.
Figure 12. Measured reactive power values of second three phase PV inverter.
Figure 13. Measured power values of second three phase PV inverter.
Table 11. Measured values for second three phase PV inverter.
Figure 14. Measured power factor values of second three phase PV inverter.
Figure 15. Voltage THD values at third stage for different PVs compared to initial conditions [%].
Table 12. Measured reactive power and PF values of second three phase PV inverter.
Table 13. Measured harmonic currents [%] of first three phase PV.
Table 14. Phase angles [˚] of harmonic currents of second three phase PV.
Table 15. Voltage THD of grid with second three phase PV inverter compared to grid without PV [%].
5. Discussion
While the discreet disturbances of harmonic distortion may not cause immediate and easily-observed impacts, it can cause some equipment to malfunction, and result in additional power losses in both customer and network equipment [17] . As harmonic levels change considerably from one week to another, it is very difficult to assess the long-term evolution of harmonic levels only from measurements carried out over a short period [1] . This paper clearly concludes that power quality problems may occur when PV utilization is not sufficiently considered.
Harmonic current angles of small generators such as PVs are seldom considered. One aim of this paper is to draw attention to this topic which could lead to advances in modelling PV inverters with different topologies. To help mitigate harmonic distortion problems, models with appropriate harmonic current amplitudes and phase angles could be used to select most suitable devices.
This study only examines one household and one PV at time. The described effects may escalate when a larger number of devices are considered. Special attention is need in situations where devices have similar harmonic patterns and the harmonic cancellation effect is minimal. Additional measurements should be performed to obtain unified values for modelling PV generators more accurately. It would be necessary to have measurement data extending over entire years in order to acquire results independent of any disturbance. Furthermore, flicker and voltage level issues should be accounted for as they may have a significant influence in real applications.
6. Conclusions
Firstly, it can be concluded that current harmonic distortion of the PV’s output is correlated with current. Distortion decreases when the PV is operating at a higher loading level. PVs function accurately under ideal conditions. Due to unstable energy availability (i.e., variable solar radiation), continuous variation in power quality parameters is to be expected. In the presented research, two PVs showed considerable harmonic current distortion (average THD over 5%) even at full loading. Only one PV had average current THD under 2% which was considered a very good achievement.
All of the measured PV systems had quite different harmonic patterns when compared with each other throughout their loading range. As such, it is difficult to propose simplified values for modelling without measuring and analysing a greater number of devices. Also, for more reliable harmonic current phase angle data, laboratory tests should be performed.
Secondly, contrary to theory, reactive power generation of PVs was not observed to be correlated to active power. Measured devices showed different levels and variation of reactive power in different phases. These differences may be hazardous in cases where high reactive power values and variations in one phase and zero reactive power in other another phase are not considered. It was also observed that main order reactive power was compensated more efficiently than higher order reactive power which was evident when comparing cos(φ) and PF.
Relative to the initial conditions where no PVs were installed, modelling one PV results in voltage distortion exceeding 10%. The influence is dependent on grid structure and topology of the PV. In case of PV with less distorted current working at high power level, minor improvement of voltage distortion was observed.
References
- Berthet, L., Eyrolles, P., Gauthier, J. and Sabeg, S. (2007) Harmonic Level Measurements on French Low-Voltage Networks. 19th International Conference on Electricity Distribution, Vienna.
- Aiello, M., Cataliotti, A., Favuzza, S. and Graditi, G. (2006) Theoretical and Experimental Comparison of Total Harmonic Distortion Factors for the Evaluation of Harmonic and Interharmonic Pollution of Grid-Connected Photovoltaic Systems. IEEE Transactions on Power Delivery, 21, 1390-1397. http://dx.doi.org/10.1109/TPWRD.2005.860231
- Jayasekara, N. and Wolfs, P. (2010) Analysis of Power Quality Impact of High Penetration PV in Residential Feeders. 20th Australasian Universities Power Engineering Conference (AUPEC), Christchurch.
- Rawa, M., Thomas, D. and Sumner, M. (2011) Simulation of Non-Linear Loads for Harmonic Studies. 11th International Conference on Electrical Power Quality and Utilisation (EPQU), Lisbon, 17-19 October 2011, 1-6. http://dx.doi.org/10.1109/EPQU.2011.6128915
- Renders, B., Degroote, L., Driesen, J. and Vandevelde, L. (2007) Profits of Power-Quality Improvement by Residential Distributed Generation. 42nd International Universities Power Engineering Conference, Brighton, 4-6 September 2007, 377-381. http://dx.doi.org/10.1109/upec.2007.4468976
- Kütt, L., Saarijärvi, E., Lehtonen, M. and Niitsoo, J. (2013) A Review of the Harmonic and Unbalance Effects in Electrical Distribution Networks Due to EV Charging. 13th International Conference on Environment and Electrical Engineering (EEEIC), Wroclaw.
- Bhattacharyya, S., Cobben, S., Ribeiro, P. and Kling, W. (2012) Harmonic Emission Limits and Responsibilities at a Point of Connection. IET Generation, Transmission & Distribution, 6, 256-264. http://dx.doi.org/10.1049/iet-gtd.2011.0376
- Niitsoo, J. and Palu, I. (2011) Distorted Load Impacts on Distribution Grid. Proceedings of the 12th International Scientific Conference Electric Power Engineering 2011, Kouty nad Desnou.
- Yong, J., Chen, L. and Chen, S. (2010) Modeling of Home Appliances for Power Distribution System Harmonic Analysis. IEEE Transactions on Power Delivery, 25, 3147-3155. http://dx.doi.org/10.1109/TPWRD.2010.2051960
- Block, P., Salamanca, H., Teixeira, M., Dahlke, D., Shiono, O. and Dodadon, A. (2014) Power Quality Analyses of a Large Scale Photovoltaic System. The 5th International Renewable Energy Congress IREC 2014, Hammamet, 25-27 March 2014, 1-6. http://dx.doi.org/10.1109/irec.2014.6826946
- Kontogiannis, K., Vokas, G., Nanou, S. and Papathanassiou, S. (2013) Power Quality Field Measurements on PV Inverters. International Journal of Advanced Research in Electrical Electronics and Instrumentation Engineering, 2, 5301-5314.
- Anwari, M., Hamid, M. and Taufik (2008) Power Quality Behavior of Single Phase Fed Adjustable Speed Drive Supplied from Grid of PV Generation. 2nd IEEE International Conference on Power and Energy (PECon 08), Bahru.
- Hasanzadeh, A., Edrington, C. and Bevis, T. (2012) Comprehensive Study of Power Quality Criteria Generated by PV Converters and Their Impacts on Distribution Transformers. 38th Annual Conference on IEEE Industrial Electronics Society IECON 2012, Montreal.
- Fekete, K., Klaic, Z. and Majdandzic, L. (2012) Expansion of the Residential Photovoltaic Systems and Its Harmonic Impact on the Distribution Grid. Renewable Energy, 43, 140-148. http://dx.doi.org/10.1016/j.renene.2011.11.026
- Niitsoo, J., Kilter, J., Palu, I., Taklaja, P. and Kütt, L. (2013) Harmonic Levels of Domestic and Electrical Vehicle Loads in Residential Distribution Networks. Proceedings of AFRICON 2013, Mauritius, 9-12 September 2013, 1-5. http://dx.doi.org/10.1109/AFRCON.2013.6757800
- Niitsoo, J., Palu, I., Kilter, J., Taklaja, P. and Vaimann, T. (2013) Residential Load Harmonics in Distribution Grid. Proceedings of 3rd International Conference on Electric Power and Energy Conversion Systems (EPECS 2013), Istanbul, 2-4 October 2013, 1-6. http://dx.doi.org/10.1109/epecs.2013.6713054
- Nicholson, G., Gosbell, V. and Parsotam, A. (2007) Analysis of Harmonic Distortion Levels on a Distribution Network. Power Engineering Conference, AUPEC 2007, Perth, 9-12 December 2007, 1-7. http://dx.doi.org/10.1109/aupec.2007.4548035