Smart Grid and Renewable Energy
Vol.06 No.05(2015), Article ID:56781,7 pages
10.4236/sgre.2015.65011
Situational Awareness Using DBSCAN in Smart-Grid
Ranganath Vallakati, Anupam Mukherjee, Prakash Ranganathan
Department of Electrical Engineering, University of North Dakota, Grand Forks, USA
Email: ranganath.vallakati@my.und.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2015; accepted 26 May 2015; published 29 May 2015
ABSTRACT
Synchrophasors are the state-of-the-art measuring devices that sense various parameters such as voltage, current, frequency, and other grid parameters with a high sampling rate. This paper pre- sents an approach to visualize and analyze the smart-grid data generated by synchrophasors using a visualization tool and density based clustering technique. A MATLAB based circle representation tool is utilized to visualize the real-time phasor data generated by a smart-grid model that mimics a synchrophasor. A density based clustering technique is also used to cluster the phasor data with the aim to detect contingency situations such as bad-data classification, various fault types, deviation on frequency, voltage or current values for better situational alertness. The paper uses data from an IEEE fourteen bus system test-bed modeled in MATLAB/SIMULINK to aid system operators in carrying various predictive analytics, and decisions.
Keywords:
Clustering, Density Based Clustering (DBSCAN), IEEE Test-Bed, Phasor Measurement Unit, Visualization

1. Introduction
Wide Area Management Systems (WAMS) are being developed by upgrading the existing power grids to enhance the abilities of the grids. Synchrophasors are the units that have the ability to measure various parameters such as voltage, current, and frequency of the lines at a sampling rate of 30 to 120 samples per second [1] . These synchrophasors play a vital role in managing the WAMS because the system can be managed only if the operators know the status of the grid. The time-tagged measurements from the synchrophasors can be used for many power system applications such as State Estimation (SE) [2] -[4] , Load Forecasting (LF), fault detection, micro-grid operations [5] -[8] , etc. Using synchrophasor data, voltage stability assessment technique has been proposed in [9] . An algorithm has been developed to detect and locate the faults on the transmission lines using the phasor data in [10] . A RTU/SCADA system can provide around 30 samples for 5 minutes, while the same number of samples is provided by the synchrophasor in a second with minimum capabilities. This makes a major difference for the operators as each and every detail can be known using the synchrophasors. Even though synchrophasors provide power system information at a large sampling rate, they can be useful only if the operators know how to utilize the data. This paper addresses the two major challenges the operators face with the synchrophasor data. The first problem is to monitor the continuous streaming of data. Recently, a method for interpreting and visualizing the synchrophasor data using Hilbert analysis has been developed in [11] . This problem of visualizing of real-time data is addressed by circle representation. The second problem is analyzing the data for system applications. This analysis is performed using a statistical approach called as density based clustering algorithm. The phasor data utilized to visualize and cluster the data are generated from a MATLAB based Simulink model of IEEE fourteen bus system. The rest of the paper is organized as follows. Section 2 explains the modeling of IEEE bus system. Section 3 describes the visualization forms developed in SIMULINK/ MATLAB and Section 4 covers the density based clustering technique that is applied on phasor data from test- bed. Sections 5 discusses the results generated using the clustering technique and Section 6 concludes the paper.
2. Bus System
2.1. IEEE Fourteen Bus System
The IEEE fourteen Bus Test Case [12] is a widely accepted standard system for power system experiments such as load flow studies, and economic dispatch. The system has fourteen buses, five generators and eleven loads [12] . The IEEE fourteen bus system model in MATLAB uses the three-phase constant voltage sources as generators. These voltage sources are programmed to provide specified voltage, current and power levels. The voltage and current waveforms at all busses are observed individually using scopes As the IEEE system is a balanced three-phase systems, the phase currents, and voltages are symmetrical in nature with 120 degrees apart at any given instant of time.
2.2. Fourteen Bus System with Contingencies
Figure 1 represents a fourteen bus system developed in MATLAB. The model has built-in random generators,
Figure 1. IEEE fourteen bus system with contingencies.
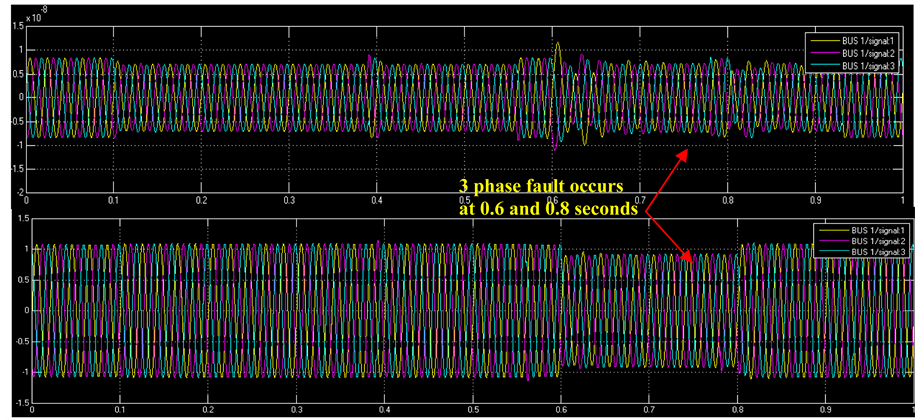
and load points which are added and removed to specific busses during the simulation period. There are several conditions such as fault types, topology, generation, and load changes) introduced into the IEEE test system. The colored blocks in Figure 1 aid in simulating the above conditions. Figure 2 represents the voltage and current waveforms at bus 1. The simulation model is tested, and ran for a 1 second period with a sampling period of 0.02. The top section of the scope in Figure 2 represents the voltage in p.u. versus time while the bottom of the scope shows the current versus time. The unsymmetrical waveforms are the result of settings in the system. Table 1 displays the measured values at bus 1.
3. Data Visualization
Data visualization (DV) is the study of the visual representation of data. The main purpose of DV is to transform the complicated information into a visually interesting representation for human observation and understanding. Generally, synchrophasors stream the grid data continuously to the operations center at a very high sampling rate. In order to make use of streaming phasor data, a tool is needed to be developed that would meaningfully represent the data streamed in from the synchrophasors for the system operators to monitor. The authors here develop a unique tool based on MATLAB in order to monitor the grid data. Representation can be in any form but it needs to communicate the information of all the data precisely [13] . Different approaches such as contour plots, maps, and diagrams are in use. However, visualizing the power system data is complicated due to the fact that it has multiple values referring to a particular parameter.
Circle Representation
The circle representation is the process of representing the angular value in conjunction with a scalar quantity. For suppose, a voltage phasor at any point has a phase angle as well as the magnitude. Phase angle generally varies from 0 to 360 degrees (−π to +π) and the magnitude is always positive. Thus, visualizing the voltage phasor in terms of circle forms a perfect DV. First three columns of Table 1 show the magnitudes that form the radius of the tri-colored lines drawn from the center of the circle while the other columns represent the corresponding angular value θ for their respective magnitude values. The MATLAB codes written to visualize the data using the Compass command function. Figure 3 shows the DV using the circle representation from the fourteen buses in the IEEE test bed. Each Circle has three arrows in three colors, red, green, and blue representing the three voltage phasors at each bus. The figure also displays the values of magnitudes of each phase and the time individually written as shown in the figure.
4. Data Mining
Data Mining (DM) is a process of extracting useful information from the data-sets. The DM is used in various disciplines such as medicine, engineering and technology, sciences, many more. DM is mainly categorized into two types. They are: data classification and data clustering [14] . Classification is a supervised learning process where the data is analyses to aid in predicting categorical labels and developing prediction models. While clustering is an unsupervised learning process of grouping data into clusters that have high similarities [15] . The similarity indices are generally the various characteristics of the data objects such as weights, distances etc. This process of grouping a set of data entities into clusters of similar objects is called clustering. A cluster of data objects can be treated collectively as one group and so may be considered as a form of data compression. There are a number of algorithms for DM but most widely techniques have been referred in [16] . Clustering schemes
Table 1. Three phase voltage magnitudes.
Figure 2. Voltage and current waveforms at bus 1.
Figure 3. Circle representation of voltage phasors at fourteen buses.
advantageous over the classification techniques if the data properties are not known. These clustering techniques are also adaptable to changes and helps single out useful features that dissimilar clusters. If one want to discover cluster or groups of data with arbitrary shapes, then density based algorithms are one of the best methods available. These typically regard clusters as dense regions of objects in the data space that are separated by regions of low density (representing noise). The algorithm this paper considers is called as Density-Based Spatial Clustering of Applications with Noise (DBSCAN). The MATLAB function for DBSCAN utilized for our data clustering.
DBSCAN
DBSCAN is a density based clustering algorithm that forms clusters based on the density of data points [17] . The algorithm grows regions with sufficiently high density into clusters and discovers clusters of arbitrary shape in spatial databases with noise. It defines a cluster as a maximal set of density-connected points.
1) Minimal requirements of domain knowledge to determine the input parameters.
2) Discovery of arbitrary shaped clusters because; the shape of clusters in spatial databases can be more than circular in nature.
3) Good efficiency on large databases.
DBSCAN considers two parameters as input excluding the data needed to cluster. They are ε (Eps) and MinPts. DBSCAN works with the following methodology:
Step 1: Initially, select a point arbitrarily.
Step 2: Observe all the points that are density reachable from X w.r.t ε (Eps) and MinPts
Step 3: If point X is a core point, a cluster is formed.
Step 4: If point X is a border point and no points are density reachable from , Then DBSCAN visits the next point of the data base.
Step 4: This process from step1 to step 4 is continued till all the points have been processed or when no new point can be added to any cluster.
All the points are clustered into three types that are called as Core, Border and the Noise points. Figure 4 shows an example of clustering of different type of points through DBSCAN.
The pseudo code for DBSCAN can be written as follows:
Pseudo code for DBSCAN clustering
Input: 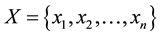 (Set of entities to be clustered)
(Set of entities to be clustered)
= Minimum distance between two points to be clustered (D).
MinPts = Minimum number of points that should be in a cluster to consider it a border group (Pt).
Output: L = 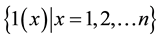 (Set of cluster labels of x)
(Set of cluster labels of x)
DBSCAN (Input Set (X), Pt, D)
foreach xi in the Input set do
If (xi is not in any cluster) then
If (xi is a core point) then
Generate a new clusterID.
Label xi with clusterID.
expandCluster (xi, X, Pt, D, clusterID)
else
label (xi, NOISE)
end
end
end
end
expandCluster (xi, X, Pt, D, clusterID)
put xi in seed queue
while the queue is not empty
extract c from the queue (where c ϵ X and c ≠ xi)
retrieve the neighborhood (eps) of c.
If there are atleast minPts neighbors
foreach neighbor n
If n is labeled NOISE
Label n with clusterID
If n is not labeled
Label n with clusterID
Put n in the queue
end
end
end
end
5. Results and Discussions
This section explains the various case studies that have been studied using DBSCAN from the data generated from IEEE fourteen bus system. The different cases study on how the DBSCAN clusters are the variations in the fourteen bus model. The four case studies considered here are:
1) Normal steady state;
2) High load condition;
3) Light load condition;
4) Fault conditions.
The test bed is run for 1 second for each case at a sampling rate of 0.02 seconds. Therefore, the granularity of the data points is very high. This data generated from the model mimics the synchrophasor data and is visualized through circle representation. It is also then provided as an input to the DBSCAN clustering algorithm. The initial parameters for the DBSCAN depend on various characteristics of the data and it is very difficult to come up with a value for them. The number of points, the threshold levels required can be the main problem solving terms and choosing the right values would give you the right output from the DBSCAN.
5.1. Case 1: Under Steady State Conditions
Under normal conditions, all the systems will be running normally and DBSCAN clusters based on its principles of core (green), border (yellow), and noise (red) data points. The left graph in Figure 5 shows the clustered output of normal condition data using DBSCAN. Data from all the fourteen buses in clustered together and all the data is clustered into core cluster due to the fact that in normal condition, the voltage stays constant around a particular value and the density of points around that value form the core points.
5.2. Case 2: Under Heavy Load Conditions
In real-world systems, heavy load conditions prevail most of the times. The power grids are often overloaded with demands over the generation capacities. The right side graph in Figure 5 represents clustered output from DBSCAN of heavy load conditioned data. The readers can find that all the line voltages have dropped from the normal level to around 0.87 p.u. By comparison with the previous graph, one can observe the shift in the density of points from 0.9 p.u to 0.87 p.u.
5.3. Case 3: Under Light Load Conditions
Light loaded situations occur when demand decreases and the generation levels remain high. The left side graph in Figure 6 shows the lightly loaded condition of the test system clustered using DBSCAN. The density of
Figure 4. DBSCAN-cluster categories.
Figure 5. Steady state and heavy load conditions.
Figure 6. Light load and fault conditions.
points in this light-load condition are shifted towards higher voltages. In comparing Figure 5 and Figure 6, readers can find the level shift between the densities of points from 0.98 p.u to 1.07 p.u.
5.4. Case 4: Under Fault Conditions
A fault condition in the test system refers to a three phase to ground fault that occurs during the time span of 0.6 and 0.7 seconds on the two transmission lines in the system. The right side graph of Figure 6 displays the DBSCAN output of the fault condition wherein at the time of fault, the voltage drops from 1 p.u to 0 p.u. DBSCAN successfully captures the fault condition and groups them into noise (red) cluster.
6. Conclusion
This paper emphasizes the need of the data mining for the smart-grid. An application of density based clustering algorithm, DBSCAN, has been proposed, and different case studies have been developed using the IEEE test system in MATLAB to study the DBSCAN clustering characteristics for the smart-grid data. The authors are also developing a data analysis framework for smart-grid with wide ranging data mining and visualizing techniques that will be made available for system operators.
Acknowledgements
This research work is possible with grant support from ND EPSCoR (UND0014140) and the Office of the VP (21418-4010-02294).
References
- Phadke, J. and Thorp, A.G. (2008) Synchronized Phasor Measurements and Their Applications.
- Abur, A. and Galvan, F. (2012) Synchro-Phasor Assisted State Estimation (SPASE). IEEE PES Innovative Smart Grid Technologies (ISGT), Washington DC, 16-20 January 2012, 1-2.
- Zhao, L. and Abur, A. (2005) Multi Area State Estimation Using Synchronized Phasor Measurements. IEEE Transactions on Power Systems, 20, 611-617.
- Report, F.P. (1996) Optimal Placement of Phasor Measurement Units for State Estimation.
- Al Karim, M., Chenine, M., Zhu, K., Nordstrom, L. and Nordström, L. (2012) Synchrophasor-Based Data Mining for Power System Fault Analysis. 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, 14- 17 October 2012, 1-8.
- Al-Mohammed, A.H. and Abido, M.A. (2014) An Adaptive Fault Location Algorithm for Power System Networks Based on Synchrophasor Measurements. Electric Power Systems Research, 108, 153-163. http://dx.doi.org/10.1016/j.epsr.2013.10.013
- Burnett, R.O., Butts, M.M. and Sterlina, P.S. (1994) Power System Applications for Phasor Measurement Units. IEEE Computer Applications in Power, 7, 8-13.
- Liu, X.A., Laverty, D. and Best, R. (2014) Islanding Detection Based on Probabilistic PCA with Missing Values in PMU Data. IEEE PES General Meeting | Conference & Exposition, National Harbor, 27-31 July 2014, 1-6.
- Dasgupta, S., Paramasivam, M., Vaidya, U. and Ajjarapu, V. (2014) Real-Time Monitoring of Short-Term Voltage Stability Using PMU Data. IEEE PES General Meeting | Conference & Exposition, 1.
- Yu, C.S., Liu, C.W., Yu, S.L. and Jiang, J.A. (2002) A New PMU-Based Fault Location Algorithm for Series Compensated Lines. IEEE Transactions on Power Delivery, 17, 33-46.
- Messina, A.R., Member, S., Vittal, V. and Ruiz-vega, D. (2006) Interpretation and Visualization of Wide-Area PMU Measurements Using Hilbert Analysis. IEEE Transactions on Power Systems, 21, 1763-1771.
- 14 Bus Power Flow Test Case. [Online] http://www.ee.washington.edu/research/pstca/pf14/pg_tca14bus.htm
- Data Visualization. [Online] http://en.wikipedia.org/wiki/Data_visualization
- Jiawei Han, M.K. (2011) Data Mining: Concepts and Techniques: Concepts and Techniques. 3rd Edition, Elsevier, Amsterdam.
- Hoaglin, D.C., Mosteller, F. and Tukey, J.W. (1983) Understanding Robust and Exploratory Data Analysis. Wiley, Hoboken.
- Wu, X., Kumar, V., Ross Quinlan, J., Ghosh, J., Yang, Q., Motoda, H., McLachlan, G.J., Ng, A., Liu, B., Yu, P.S., Zhou, Z.-H., Steinbach, M., Hand, D.J. and Steinberg, D. (2007) Top 10 Algorithms in Data Mining. Knowledge and Information Systems, 14, 1-37. http://dx.doi.org/10.1007/s10115-007-0114-2
- Ester, M., Kriegel, H., Sander, J. and Xu, X. (1996) A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. Kdd.