Smart Grid and Renewable Energy
Vol.06 No.08(2015), Article ID:58797,16 pages
10.4236/sgre.2015.68020
Implementation of Dynamic Line Rating in a Sub-Transmission System for Wind Power Integration
Saifal Talpur, Carl Johan Wallnerstrom, Patrik Hilber, Christer Flood*
School of Electrical Engineering, KTH Royal Institute of Technology, Fortum Distribution AB, Stockholm, Sweden
Email: *saifal@kth.se
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2015; accepted 11 August 2015; published 14 August 2015
ABSTRACT
Based on conventional static line rating method, the actual current carrying capability of overhead conductors cannot be judged. Due to continuous increment in electricity demand and the difficulties associated with new line constructions, the overhead lines are therefore required to be rated based on a method that should establish their real-time capability in terms of electricity transmission. The method used to determine the real-time ampacity of overhead conductors not only can enhance their transmission capacity but can also help in allowing excessive renewable generation in the electricity network. In this research work, the issues related to analyzing an impact of wind power on periodical loading of overhead line as well as finding its static and dynamic ampacities with line current are investigated in detail. Moreover, the investigation related to finding a suitable location for the construction of a 60 MW wind farm is taken on board. Thereafter, the wind park is integrated with a regional grid, owned by Fortum Distribution AB. In addition to that, the electricity generated from the wind park is also calculated in this project. Later on, the work is devoted to finding the static and dynamic line ratings for “VL3” overhead conductor by using IEEE-738-2006 standard. Furthermore, the project also deals with finding the line current and making its comparison with maximum capacity of overhead conductor (VL3) for loading it in such a way that no any violation of safe ground clearance requirements is observed at all. Besides, the line current, knowing the conductor temperature when it transmits the required electricity in the presence of wind power generation is also an important factor to be taken into consideration. Therefore, based on real-time ambient conditions with actual line loading and with the help of IEEE-738-2006 standard, the conductor temperature is also calculated in this project. At the end, an economic analysis is performed to evaluate the financial advantages related to applying the dynamic line ratings approach in place of traditional static line ratings technique across an overhead conductor (VL3) and to know how much beneficial it is to temporarily postpone the rebuilding and/or construction of a new transmission line. Furthermore, an economic analysis related to wind power system is taken into consideration as well to get familiar with the costs related to building and connecting a 60 MW wind farm with the regional grid.
Keywords:
Overhead Conductor, Static and Dynamic Ampacities, Real-Time Weather Conditions, Static and Dynamic Line Rating Techniques, Wind Power Integration, Regional Grid, Line Current. Conductor Temperature, Wind Power Economics, Dynamic Line Rating Economics

1. Introduction
Power system owners are facing major challenges with changed electricity consumption patterns and increase in distributed generation [1] [2] . Furthermore, quality regulations in many countries (e.g. UK, Sweden and Norway) have increased the demand for cost efficiency and at the same time the demand for higher reliability [3] . Smart structural refurbishments are thus needed to increase the overall efficiency in the future. Today, power system capacity is set with a static limit based on worst-case scenarios. One solution to significantly decrease and/or delay future investment costs and still to meet the same requirements (increase in capacity of overhead lines) is Dynamic Rating (DR) [4] -[7] .
DR is therefore identified as an important topic in the quest for the development of the electrical grid [8] . The concept implies that the capacity of a component dynamically varies as a function of external parameters, like weather conditions and loading history [9] . Traditionally, the rating is statically set from simulations of worst- case scenarios referred to as static rating (SR) [10] . This leads to a margin between the actually available capacity and the rating itself, which is left unused [9] . The value of DR lies in utilizing existing equipment to a greater extent without passing loads which can lead to outages, broken components or extensive premature aging [9] .
The DR concept can be used on different parts of power systems; in this paper, the specific case of applying DR on power lines is referred to as DLR. Wind power rarely reaches its maximum production. By implementing DLR and correlating the new ratings with wind power generation, the estimated time/risk of “overloading” can be significantly reduced [7] ; for example, the probability is low that perfects wind conditions and extreme heat occur at the same time. This can remove or postpone some investment requirements [11] [12] . The methodology of this paper was developed around a real case study; adding 60 MW of wind power in a 130 kV sub-transmis- sion system and its impact was investigated in terms of line loading. Besides this task, the SR and DLR of an overhead conductor were calculated and compared with the line current.
2. Theory behind Dynamic Line Rating
By using equations 2.1 - 2.15 (based on IEEE-738-2006 Standard), the DLR of overhead conductors (equation 2.34) can be calculated. SI units and the specifications of the parameters used in these equations are listed in Table 1. Based on these equations (2.1 - 2.15), it will be observed that conductor temperature actually varies with respect to heat input (gain rate) and heat output (loss) sources. The heat input (heat gained by the conductor) observed across the overhead conductor is due to ohmic losses and the solar heat gain (solar radiation or solar flux) [13] . After being heated up, the heat energy gained by the conductor is lost by means of two factors, i.e. convection and radiation [13] , known as heat output sources.
According to the law of conservation of energy, there should always be a balance between heat gain and heat loss rates when not facing changes in conductor temperature, i.e. the heat balance equation 2.1 [14] must be followed at times of steady state.
 (2.1)
(2.1)
The following heat balance equation [14] represents the balance amongst heat gain and heat loss rates, i.e.
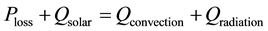 (2.2)
(2.2)
The ohmic loss 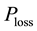 (W) causes heat gain in the conductor and is calculated based on Equations (2.3) and
(W) causes heat gain in the conductor and is calculated based on Equations (2.3) and
Table 1. Parameters for the dynamic line rating.
(2.4) [14] , i.e.
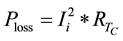 (2.3)
(2.3)
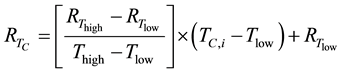 (2.4)
(2.4)
Similarly, the solar heat gain can be calculated with the help of equation 2.5 [14] . From this equation, it is observed that this heat gain  depends upon four main factors, i.e. on the projected conductor area, ability of the conductor to absorb sun rays, the conductor latitude, the number of hours of the day (having co-relation with direct sun radiation).
depends upon four main factors, i.e. on the projected conductor area, ability of the conductor to absorb sun rays, the conductor latitude, the number of hours of the day (having co-relation with direct sun radiation).
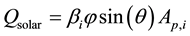 (2.5)
(2.5)
Furthermore, the heat loss rate is classified into two types, i.e. the heat loss due to convection and the heat loss due to radiation [13] . The convection heat loss rate is further classified into two types: natural convection and forced convection [9] . The natural convection heat loss rate  (W/m) is dependent upon conductor diameter, the temperature across the conductor, and the ambient temperature [14] . It can be calculated with the help of Equation (2.6) [14] :
(W/m) is dependent upon conductor diameter, the temperature across the conductor, and the ambient temperature [14] . It can be calculated with the help of Equation (2.6) [14] :
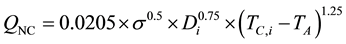 (2.6)
(2.6)
The forced convection heat loss rate mainly depends upon wind speed and its direction [13] . This heat loss rate is also classified into two categories, depending upon the magnitude of wind speed. At low wind speeds (lower than 4.47 m/sec [14] ), the forced convection heat loss rate 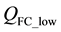 (W/m) will be calculated based on Equation (2.7) [14] :
(W/m) will be calculated based on Equation (2.7) [14] :
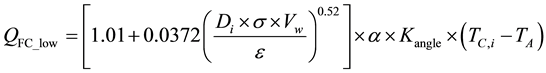 (2.7)
(2.7)
Similarly, at high wind speeds (higher than or equal to 4.47 m/sec [15] ), the forced convection 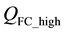 (W/m) is calculated with the help of Equation (2.8) [10] .
(W/m) is calculated with the help of Equation (2.8) [10] .
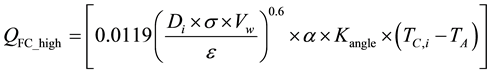 (2.8)
(2.8)
Moreover, in the case of low wind speeds, the larger of the two methods (natural or forced ventilation), should be used [14] . At zero wind speed, the forced convection heat loss rate will be zero. However, natural convection will help to reduce the conductor temperature [14] . To find the forced convection heat loss rate, the wind direction factor (Kangle) needs to be calculated, given in Equation (2.9) [14] :
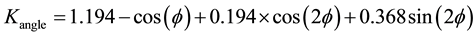 , (2.9)
, (2.9)
where 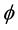 (angle between wind direction and conductor axis) is kept almost fixed, i.e. around 90˚. Equation (2.10) provides the thermal conductivity of air (
(angle between wind direction and conductor axis) is kept almost fixed, i.e. around 90˚. Equation (2.10) provides the thermal conductivity of air (

The average of ambient and conductor temperature (Tfilm) is given in Equation (2.11) [14] :

Equation (2.12) [14] represents the dynamic viscosity of surrounding air:

The air density can be calculated based on Equation (2.13) [15] :

Equation (2.14) from IEEE-standard [14] gives the radiated heat loss rate 

Like the forced convection heat loss rate, the radiated heat loss rate depends upon the difference in temperature between overhead conductors and ambient: the greater the difference, the higher the radiation heat loss rate. After establishing the heat gain and heat loss parameters, the ampacity of conductor i can be calculated based on Equation (2.15) [14] :

Based on the ampacity of the conductor as shown in Equation (2.14), it is evident that the convection and radiation heat loss rates affect the capacity of the conductor by allowing higher currents. Similarly, its ampacity is increased when the solar radiation is lower. Moreover, the thermal AC resistance also plays its role in determining the ampacity of the overhead line.
3. Implementation of a Case Study
3.1. Objectives
An important goal of this paper is to evaluate the technical and economic aspects of dynamic line rating (DLR) across an overhead conductor (VL3) in a meshed 130 kV sub-transmission electricity network after integrating 60 MW wind power with the regional grid of Fortum.
The following specific objectives were formulated in this paper:
・ Evaluation of wind speed and its direction (relative to the axis of line conductor) on wind power production.
・ Development of a system model of wind power connection to a 130 kV system.
・ Assessment of power flow study after wind power connection.
・ Economic analysis of DLR implementation compared with traditional solutions.
3.2. Overall System Introduction
The area studied (area 160) belongs to the Värmland regional power system of Fortum Distribution AB and is located in western Sweden. The operational voltage is 135 kV and incorporates both industrial and residential loads. Initially, this power system was built by several large industries (paper and steel) around the mid-20th century and expanded during the exploitation of hydropower in the region. Now, in the north of the country there is large scale hydro power generation, whereas the south is dominated by consumption of electricity. Hence, this power system connects the electric power generation from the north with the loads in the south.
Besides connections with local generation, it is also connected with other network owners, such as Norway in the west and Vattenfall in the east. The network is also connected with the Swedish national grid via two 400-kVstations. The overhead line (VL3) connects an area with mainly power production in the north to a load-focused area in the east. Furthermore, the eastern area also includes a 400-kV connection.
High stress on VL3 is observed during periods of low industrial loads and high hydropower production. The total load pattern in Värmland is found to follow annual fluctuations, as described in Figure 1. For each month, the power system balance was chosen with a load reduction according to Figure 1 and maximum power production. Thus, power system situations causing high stress on VL3 were achieved.
In Figure 1, the percentage indicates net power demand on monthly basis compared to the total connected load in the 130 kV regional network of Fortum, i.e. 910 MW in the whole year of 2012. From this figure, it is observed that during summer, power demand is comparatively lower than in the winter. The lowest power demand is observed in July with 70% load remained switched off. The real-time weather data related to ambient temperature, wind speed and its direction was first gathered before calculating the DLR. This data was based on Karlstad municipality in Sweden and was obtained from the Swedish Metrological and Hydrological Institute (SMHI) [16] .
3.3. Wind Power Information, Data and Assumptions Used in the Case Study
3.3.1. Installation of Wind Turbines
Technological advancements in power electronics have increased the scope of wind power [17] . Due to the unstable nature of wind speed and its direction, keeping the system voltage and frequency to its constant level requires frequent use of power electronic equipment [17] . With the help of power electronic converters, constant electric power is sent to the active and/or passive loads at almost constant voltage [17] . Before installing wind turbines, a suitable location for the wind farm must be decided. In order to find such a location, many factors need to be considered; some important ones [18] are:
・ A large and open flat area.
・ Access to the road to carry out flexible installation and maintenance.
・ Access to the national/regional grid.
・ Low noise effect in the area.
・ Compliance with air traffic rules.
・ Consideration of the safety rules related to falling ice.
・ Appropriate distance from protected areas.
Besides considering the technical benefits, it is important to take on board environmental and social perspectives as well, so that a widely accepted location of the wind farm is chosen. In this study, the wind farm is assumed to consist of 20 Enercon E−101 wind turbines [19] , thus having an installed nominal power of 60 MW. The wind farm is assumed to be placed at Stöpsjön in close proximity to the regional grid. After considering the planned location for the wind farm, an optimal direction of the wind turbines had to be found. This decision was based on the results from wind roses. A wind rose is actually an important tool for determining the dominant
Figure 1. Net monthly power demand in Värmland regional network.
direction of wind speeds during a single year.
In this project, the data related to wind speed and its direction was obtained from SMHI for a hub-height of 100 m. Based on this data, a wind rose was plotted with the help of Enviroware® Software and is shown in Figure 2. Based on wind roses from 2012, as shown in Figure 2, t the wind speed in this region is observed to span over an interval, with a dominant direction around 180˚ even if all wind directions are represented during a year. Enercon E−101 wind turbines are used in this project to provide the required amount of electric power (a maximum of 60 MW).
The diameter of this turbine is 101 m; an optimal distance between each of the 20 wind turbines is chosen in such a way that low wake, low noise and smaller interference effects should be observed. Based on these criteria, an optimal spacing is chosen amongst the turbines so that even at low wind speeds, sufficient power is obtained. In this project, it is assumed that a 7-rotor diameter distance is useful between the turbines located towards the main wind direction, while a 6-rotor diameter distance is optimum for the wind turbines facing an orthogonal wind direction [18] , i.e.
・ Main wind direction distance: 707 m.
・ Orthogonal wind direction distance: 606 m.
The power plants are located in two areas and based on the aforementioned distance between the installed wind turbines. Both fields are assumed to be identical in size, with total area equal to 3.427 km2. Moreover, the length of each field is found to be almost three times its width.
3.3.2. Wind Power Generation
Besides selecting a suitable location for the wind turbines, another important factor is their connection with the regional grid. This is a complex issue due to the unstable nature of wind power. The following issues from a general perspective must first be addressed properly [20] :
・ Power quality problems in terms of voltage dips and frequency variations.
・ Due to difficulties in predicting the wind power production, operation of power system can be significantly affected.
・ The considerable impact of wind inconsistency on system operating costs.
・ Power imbalance issues, i.e. more wind power generation than required or vice versa.
・ The need for reliable transmission planning to allow the electric power to flow from generation sources to load points.
Figure 3 illustrates the wind speed and the generation during 2012. It is evident that the maximum wind speed at 100 - 110 meters of hub-height was obtained around 14 m/sec with the lowest around 1.5 m/sec. Another important observation from the graph is the trend of wind speeds with respect to variations in the
Figure 2. Wind Roses showing the wind direction at Stöpsjön.
Figure 3. Wind speed versus power generation.
seasons. Similarly, the average wind speed during the whole year is observed to be around 6 m/sec.
3.3.3. Wind Energy Output
Two important inputs from the projected wind farm site are required for calculating the annual electricity output: 1) the power curve of the wind turbine and 2) the annual frequency distribution of the wind speeds. Both of these factors may help in providing a sufficient prognosis of electricity that a wind turbine can generate when installed at the given site [18] . A power curve gives an a rough estimate of the electric power that a wind turbine is expected to produce at different wind speeds [18] , whereas the frequency distribution provides information regarding wind speeds at a site and information on how many hours a year the wind will blow at a certain wind speed [18] .
From the power curve shown in Figure 4, it is evident that the cut-in speed of an E−101 wind turbine is around 3 m/sec, i.e. when the turbine starts to generate electricity. Moreover, it indicates that the turbine is able to generate maximum (nominal) output power when it experiences a wind speed of around 12 m/sec. Table 2 indicates the wind speed intervals and the annual frequency distribution with calculated power for the year of 2012 for the aforementioned type of wind turbines located in the specified wind farm area.
Based on data from Table 2, the annual electricity production is calculated to be around 68.19 GWh. Furthermore, in Table 3 and Table 4, wind speed values across VL3 conductor and in the wind farm are mentioned for the whole year of 2012 (the data obtained from SMHI [16] ).
3.4. Dynamic Line Rating Approach Applied in the Case Study
3.4.1. Weather Based Dynamic Rating
The ampacity of a power system conductor is its ability to carry the maximum RMS (root mean square) current continuously without exceeding the temperature limit [21] . Hence, it limits the actual capability of transmitting electric power [22] . If the real-time weather-based information is used in place of fixed assumptions, then actual capacity of overhead lines can be obtained. This study is developed on the basis of equations provided in IEEE-738-2006 standard (see section0) [14] and the real-time weather data [22] . Mainly, DLR is used for two
Figure 4. Power curve of enercon e−101 wind turbine [14] .
Table 2. Annual frequency distribution of wind speeds.
Table 3. Wind Speed [m/s] across Line VL3 and the wind farm from January to June 2013.
*Wind Speed across line (VL3) [m/s]. **Wind Speed across wind farm [m/s].
purposes: first, to increase the capacity of overhead conductor in terms of transmitting the maximum electric current and second, to help in the transfer of electricity during peak load and emergency states [22] .
To gain an overall picture of the changes in conductor (VL3) ampacity based on SLR assumptions, see Table 5. The results shown in Table 5 are calculated based on typical fixed weather assumptions, i.e. the highest ambient temperature, the lowest wind speed and the maximum solar radiation (during daytime) for a 30-kilometer long ACSR overhead conductor. Furthermore, it is observed from Table 5 that wind speed and its direction has
Table 4. Wind Speed [m/s] across Line VL3 and the wind farm from July to December 2013.
*Wind Speed across line (VL3) [m/s]. **Wind Speed across wind farm [m/s].
a huge impact on increasing or decreasing the conductor ampacity compared with changes in ambient temperature.
Low ambient temperature combined with high wind speed and its direction (perpendicular to the position of the conductor) increases the conductor ampacity significantly.
3.4.2. Line Current
Line current represents the flow of current through a conductor during normal state in the power system. In this
Table 5. A typical example of weather effect on lineampacity, VL3 OH-line (30 km) with SLR assumptions: 30˚C, 0.6 m/sec and Day-time.
project, line current was changed by varying the loads in the region around VL3. The load situation was adjusted according to the philosophy discussed in section 3.2. After variations in the system loads and by addition of wind power generation, the current and temperature across “VL3” overhead line were analyzed. Line currents were calculated with PSS/E® (power system simulation) software.
The 60 MW wind farm was connected at 10 km distance from VL3 overhead line conductor in Fortum’s 130 kV regional network. The network was simulated in PSS/e® software in the presence of wind farm. Besides the effect of wind power on line loading, the effect of loads connected in 130 kV regional network was also investigated in this research work. The rating of these loads was observed for both summer and winter case scenarios. Furthermore, the critical span of VL3 was considered around 6 m. Hence, loading of VL3 line conductor as well as its dynamic ampacity was calculated based on its critical span.
3.4.3. Static and Dynamic Ampacities
The dynamic and/or static ampacity is based upon two main factors, i.e. physical characteristics of the conductor and environmental parameters [9] , with sub categories such as conductor diameter, conductor temperature, ambient temperature, wind speed, angle between wind speed and conductor, and solar radiation. The dynamic and static line ampacities for VL3 overhead line are calculated in this section in addition to line current (based on the monthly load changes and the hourly wind power generation), which is illustrated in Figure 5. Note that the static rating is not totally static since it is divided into one static “winter” and one static “summer” rating.
Regarding network operations, the analysis shows that during winter, the dynamic and even the static line ampacity is sufficient in terms of electricity flow through the overhead conductor as required based on the load demand. However, in summer, the situation is different, due to excessive ambient temperature: the line cannot be allowed to transmit the required flow of electricity due to the risk of conductor deterioration or sag problems.
As Figure 5 shows, in winter, both SLR and DLR are higher than the line current and hence the line can be loaded up to its full capacity without any risk during this period. However, during summer timings, the line cannot be allowed to carry the required current (as is clear from the graph, both SLR and DLR are seen to be lower than the line current). The significance of this graph is that with the traditional approach, network operators need to consider corrective actions or curtailments during all summer months. With DLR, corrective actions or curtailments are only necessary during a few summer days.
4. Economic Analysis of Ampacity Upgrading Methods
4.1. Introduction
Based on technological advancements in the wind energy sector, the cost of electricity produced from wind power is significantly reduced: one seventh of the electricity cost in the early eighties [23] . When carrying out an economic analysis of the wind power system, it should be checked whether this project will be profitable (even on a short-term basis) or not from an economic perspective. The decision -making plays a vital role in this regard and needs to take into account the interests of all the stakeholders involved. From a wind farm owner’s perspective, the economic analysis of wind power generation involves three main categories of economic costs [20] :
・ Capital costs related to construction of the wind farm.
・ Fixed operation costs.
・ External costs of the wind power generation (termed the leakage costs).
Figure 5. Static and Dynamic Ampacities (A) versus the Line Current (A) in 2012.
In this project, besides wind power analysis, the DLR approach is also taken into account. Based on DLR, better information on the actual ampacity of an overhead line may allow an increased flow of energy. A direct economic advantage for a DSO can be to save money in the short or long term by postponing or avoiding upgrade of existing line (s) or construction of new line (s). Moreover, the delay in investments may help in enhancing the effectiveness of spent money [11] . However, since power system infrastructure is a regulated natural monopoly, it can be difficult to estimate exactly the share of the benefits each stakeholder receives. From a DLR perspective, many financial benefits can be directly or indirectly achieved (depending on the type of regulation) [11] .
・ Cheaper electricity for consumers (a DLR advantage for society).
・ Better prices for the wind power owners (in terms of lower connection fee).
・ Improvement in economic use of transmission lines (useful for the DSO).
・ Making asset utilization cost effective (valuable from a DSO perspective).
4.2. Economic Analysis of Ampacity Upgrading Methods
4.2.1. Introduction
By adopting the DLR approach, the capacity of an overhead conductor is increased to a significant extent by allowing the transfer of more electric power [12] . Other options if the capacity needs to be increased are to replace the existing conductor with a high temperature-sustaining conductor or to construct a new line in parallel with the existing conductor. The hypothesis is that these kinds of solutions are less appropriate from economic, environmental and social perspectives [11] . DLR allows operators opportunities for delivering more power during its peak demand and avoiding unnecessary load shedding under contingency conditions [24] . Similarly, the power capacity limitations for any DSO can also be expensive, while a small increase in the capacity of the overhead lines may have significant economic effects [19] . In the following sections, annual revenue based on increment in capacity is calculated, both for a DLR approach to an existing conductor (VL3) and for traditional solutions, including investing in a new overhead conductor (area 593 mm2). Finally, the economic value of postponing the power system investments will also be taken into account.
4.2.2. Net Annual Income Based on the DLR Approach
The dynamic ampacity in this project was calculated for the whole year of 2012 and was based on a particular hour of the day. The selection of that hour was assumed as random and was chosen within a 13-hour range (7 am to 7 pm). Based on this ampacity rating, the allowed energy flow 
Similarly, based on the static ampacity rating, the allowed energy flow 
From the calculations of 

Furthermore, applying the real-time dynamic rating technique across an existing overhead conductor requires equipping the line with useful communication and computer tools for transferring the real-time data from the line corridor to the control room. The different monitoring and communication tools are available in this regard; CAT-1 transmission line monitoring system is one of them [25] . If these tools are installed across an existing overhead conductor for continuous real-time monitoring and transmission of data to the DSO’s control center then it costs around $200,000 (one time product cost estimation) for a single existing transmission line conductor (excluding the shipment, installation and O&M costs) [20] . Now converting it to SEK (1 SEK ≈ $0.15), the first time expenditure 
With the help of the DLR technique, the transfer of electricity through the existing overhead conductor is significantly higher than its flow based on the traditional SLR approach. The net annual income 


Furthermore, due to the involvement of different stakeholders in the electricity market, it is difficult and complex to estimate the income or profit for each stakeholder involved, i.e. how much share should be allocated to the wind power owners, the utilities and the DSOs when the energy is transferred based on the DLR approach (particularly due to its dynamic nature). Hence, to avoid such assumption-based profits or incomes for each stakeholder, it is better to focus on the economic analysis based on the benefit of capacity increase across an overhead line. This financial benefit after implementation of the DLR approach across the existing overhead line (VL3) is now calculated as:

4.2.3. Net Annual Income in Case of Upgrading the Line
The allowed energy flow 
Replacement of the existing line “VL3” with a new conductor that has an area of 593 mm2 and the length of 30 km will require an approximate total capital cost 
Assuming that the cost related to upgrading the conductor is financed by a loan at a nominal interest rate of 7.5% (real interest rate + expected inflation) and the loan is required to be paid in a period of 20 years, then, based on this data, the capital cost of upgrading the conductor on annual basis 

where a is the annuity, r is the nominal interest rate, and n is the pay-back period in years. Based on Equation (4.1), the annuity will be:
After calculation of the annuity, the annual capital cost of replacing the existing overhead conductor (VL3) with a new overhead conductor (of area 593 mm2) can be calculated with the help of Equation (4.2) [18] , i.e.

After replacement of the existing conductor with a new overhead line that has 1.1 times larger cross-sectional area, the transfer of electricity (based on SLR approach) through this new overhead line is increased significantly compared to its flow through the existing smaller cross-sectional area overhead line. Moreover, the energy (based on static ampacity) that is curtailed by existing conductor 
or,
where 

Based on this value, it is observed that, after the upgrading of the existing conductor, an increment of 1 GW∙h energy flow through the new overhead line may yield a theoretic maximal benefit of 0.14 MSEK during a single year.
4.2.4. Net Annual Income in Case of Building a New Line
An approximate total capital cost 
Similar to upgrading of the line, if the construction of a new overhead conductor is financed in the form of a bank loan at a nominal interest rate of 7.5% with a pay-back period of 20 years, then the annual capital cost 
where,
Hence, the annual capital cost for the new line construction will be:
After construction of a new overhead line with 1.1 times larger cross-sectional area, the transfer of electricity (based on the SLR approach) through this new overhead line is significantly increased compared with its flow through the existing smaller cross-sectional area overhead line. Furthermore, the energy (based on static ampacity) that is curtailed by existing conductor 
or
where 

Based on this value, it is observed that an increment of 1 GW∙h energy flow through the new overhead line may yield a theoretical benefit of 0.09 MSEK during a single year.
4.2.5. Comparison amongst Ampacity Upgrading Methods
In this section, a comparison amongst different ampacity upgrading techniques is taken into account. The ampacity upgrading methods for replacement of a smaller overhead conductor with a new larger overhead conductor and new line construction are considered as conventional approaches for the transmission of electricity that otherwise cannot be transferred through the old smaller overhead conductor. From a technical perspective, any of these conventional ampacity-upgrading methods can be considered useful in terms of required electricity transmission but from an economic perspective, these methods are less desirable. In comparison with conventional ampacity upgrading methods, it is observed that the dynamic line rating approach is not only useful from a technical perspective but also feasible from an economic perspective. Furthermore, Table 6 gives an overall picture of the annual benefit from the increase in conductor capacity with the help of different ampacity upgrading methods.
From Table 6, it is observed that the DLR approach is significantly profitable in comparison to conventional ampacity upgrading techniques. However, on the basis of limited information, it is difficult to find and compare the exact turnovers from the aforementioned ampacity upgrading techniques. For example, the energy transfer through conductor replacement or through a new line construction is based on a static ampacity approach which may yield the predictable revenue, whereas the revenue based on dynamic line ampacity cannot be predicted due to significant variations in the conductor capacity.
Therefore, the revenue-based comparison cannot be estimated amongst static and dynamic line ratings. Moreover, the cost of dynamic rating equipment and their control room issues are uncertainties when estimating the profits obtained from the dynamic line ratings compared with the profits based on conventional static ampacity techniques. Therefore, these figures cannot be regarded as reliable and may differ in reality.
Table 6. Annual benefit from ampacity upgrading solutions.
5. Conclusions
This paper presented analysis results from an application study where dynamic line rating was implemented across an overhead line located in a 130 kV sub-transmission system. The static as well as dynamic ampacities has been calculated to estimate the accurate range of loading an overhead line throughout the whole year. The application study also investigated the integration of a 60 MW wind power park. Based on wind power production and power demand in the system, the line current and conductor temperature has been calculated. Thereafter, a comparison amongst conductor ampacities and the line current was carried out to investigate how much further the overhead conductor can be rated (loaded).
The results of this paper indicate that dynamic line rating significantly has the potential to improve the capacity of a power component (here exemplified by an overhead conductor) and to facilitate wind power integration. During winter, due to low ambient temperature and minimum solar radiation, the dynamic ampacity of an overhead conductor is found to be many times higher than its static ampacity. However, during peak summer days, both ampacity ratings are almost identical and lower than actual line current.
From an economic study, it is observed that the ampacity upgrading of an overhead conductor on the basis of dynamic rating is significantly profitable in comparison with conductor replacement or new line construction techniques. The main contribution of the paper is to combine theoretical calculations and modeling with real application. Besides received results and conclusions, data from this paper can be valuable because of reference material within other studies of wind power and/or dynamic rating.
Cite this paper
SaifalTalpur,Carl JohanWallnerstrom,PatrikHilber,ChristerFlood, (2015) Implementation of Dynamic Line Rating in a Sub-Transmission System for Wind Power Integration. Smart Grid and Renewable Energy,06,233-249. doi: 10.4236/sgre.2015.68020
References
- 1. Ipakchi, A. and Albuyeh, F. (2009) Grid of the Future. IEEE Power and Energy Magazine, 7, 52-62.
http://dx.doi.org/10.1109/MPE.2008.931384 - 2. Lopes, J.A., Hatziargyriou, N., Mutale, J. et al. (2007) Integrating Distributed Generation into Electric Power Systems: A Review of Drivers, Challenges and Opportunities. Electric Power Systems Research, 77, 1189-1203.
http://dx.doi.org/10.1016/j.epsr.2006.08.016 - 3. Wallnerström, C.J. (2011) On Incentives affecting Risk and Asset Management of Power Distribution. PhD Thesis, KTH, Stockholm.
- 4. Shaker, H., Fotuhi-Firuzabad, M. and Aminifar, F. (2012) Fuzzy Dynamic Thermal Rating of Transmission Lines. IEEE Transactions on Power Delivery, 27, 1885-1892.
- 5. Simms, M. and Meegahapola, L. (2013) Comparative Analysis of Dynamic Line Rating Models and Feasibility to Minimise Energy Losses in Wind Rich Power Networks. Energy Conversion and Management, 75, 11-20.
http://dx.doi.org/10.1016/j.enconman.2013.06.003 - 6. Michiorri, A., Currie, R. and Taylor, P. (2011) Dynamic Line Ratings Deployment on the Orkney Smart Grid. Proceedings of the 21st International Conference on Electricity Distribution, Frankfurt, 6-9 June 2011.
- 7. Wallnerström, C.J., Huang, Y. and Söder, L. (2014) Impact from Dynamic Line Rating on Wind Power Integration. IEEE Transactions on Smart Grid, 6, 343-350.
- 8. Wallnerström, C.J., Hilber, P., Söderström, P., Saers, R. and Hansson, O. (2014) Potential of Dynamic Rating in Sweden. Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, 7-10 July 2014, 1-6.
http://dx.doi.org/10.1109/pmaps.2014.6960605 - 9. Holbert, K.E. and Heydt, G.T. (2001) Prospects for Dynamic Transmission Circuit Ratings. Proceedings of the 2001 IEEE International Symposium on Circuits and Systems, Sydney, 6-9 May 2001, 205-208.
http://dx.doi.org/10.1109/iscas.2001.921283 - 10. Douglass, D.A. (1988) Weather-Dependent versus Static Thermal Line Ratings (Power Overhead Lines). IEEE Transactions on Power Delivery, 3, 742-753.
- 11. Sandy, K.A. (2010) Dynamic Line Ratings for Optimal and Reliable Power Flow, Enhanced Power Flow for the Smart Grid. Proceedings of the FERC Technical Conference, Washington DC, 24 June 2010.
- 12. Kim, S.D. and Morcos, M.M. (2013) An Application of Dynamic Thermal Line Rating Control System to Up-Rate the Ampacity of Overhead Transmission Lines. IEEE Transactions on power delivery, 28, 1231-1232.
- 13. Merrell, J., Mike P.D. and Jared R.J. (2008) Dynamic Line Ratings for the Cowlitz-LaGrande Transmission Lines. Washington State University, Washington DC.
- 14. IEEE (1993) IEEE Standard for Calculating the Current-Temperature of Bare Overhead Conductors. IEEE, New York, c1-59.
- 15. Talpur, S. (2013) Dynamic Line Rating Implementation as an Approach to Handle Wind Power Integration: A Feasibility Analysis in a Sub-Transmission System Owned by Fortum Distribution AB.
- 16. SMH (2012) Swedish Metrological and Hydrological Institute.
http://www.smhi.se - 17. Blaabjerg, F., et al. (2006) Power Electronics in Wind Turbine Systems. The Proceedings of the IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, 14-16 August 2006, 1-11.
- 18. Wizelius, T (2007) Developing Wind Power Projects: Theory and Practice. Routledge, London.
- 19. Enercon Product Overview. E-101 Wind Turbine.
http://www.enercon.de/p/downloads/ENERCON_PU_en.pdf - 20. Deutsche Gesellschaft für Technische Zusammenarbeit (GTZ) GmbH (2006) Feasibility Study for Wind Park Development in Ethiopia and Capacity Building. Mesobo-Harena Wind Park Site.
- 21. Williams, N. and Jeffrey, S. (2007) NEC Q & A: Questions & Answers on the National Electrical Code. Jones & Bartlett Learning, Burlington.
- 22. Kim, D.-M., et al. (2006) Prediction of Dynamic Line Rating Based on Assessment Risk by Time Series Weather Model. Proceedings of the PMAPS 2006 International Conference on Probabilistic Methods Applied to Power System, Stockholm, 11-15 June 2006, 1-7.
http://dx.doi.org/10.1109/pmaps.2006.360329 - 23. Georgilakis, P.S (2008) Technical Challenges Associated with the Integration of Wind Power into Power Systems. Renewable and Sustainable Energy Reviews, 12, 852-863.
http://dx.doi.org/10.1016/j.rser.2006.10.007 - 24. Douglass, D.A., et al. (2000) Dynamic Thermal Ratings Realize Circuit Load Limits. Computer Applications in Power, IEEE, 13, 38-44.
http://dx.doi.org/10.1109/67.814665 - 25. Seppa, T.O. (2007) Reliability and Real Time Transmission Line Ratings. Nexans, Ridgefield.
- 26. (2013) Nord Pool Spot, Elspot Prices (EUR/MWh).
http://www.nordpoolspot.com/Market-data1/Elspot/Area-Prices/ALL1/Hourly/
NOTES
*Corresponding author.
































