Smart Grid and Renewable Energy
Vol.4 No.4(2013), Article ID:33931,8 pages DOI:10.4236/sgre.2013.44039
A Bivariate Chance Constraint of Wind Sources for Multi-Objective Dispatching
![]()
Electrical Power and Machine Department, Faculty of Engineering, Cairo University, Cairo, Egypt.
Email: eng.m.elshahed@gmail.com
Copyright © 2013 Mostafa Elshahed et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 5th, 2013; revised June 5th, 213; accepted June 14th, 2013
Keywords: Correlated Weibull Distribution; Economic Emission Dispatch; Stochastic Programming; Wind Power
ABSTRACT
The economic emission dispatch (EED) problem minimizes two competing objective functions, fuel cost and emission, while satisfying several equality and inequality constraints. Since the availability of wind power (WP) is highly dependent on the weather conditions, the inclusion of a significant amount of WP into EED will result in additional constraints to accommodate the intermittent nature of the output. In this paper, a new correlated bivariate Weibull probability distribution model is proposed to analytically remove the assumption that the total WP is characterized by a single random variable. This probability distribution is used as chance constraint. The inclusion of the probability distribution of stochastic WP in the EED problem is defined as the here-and-now strategy. Non-dominated sorting genetic algorithm built in MATLAB is used to handle the EED problem as a multi-objective optimization problem. A 69-bus ten-unit test system with non-smooth cost function is used to test the effectiveness of the proposed model.
1. Introduction
Wind energy is the most attractive clean and fuel-free solution to the world’s energy challenges. Well established in more than 50 countries all over the world, supplying more than 250 GW as total installed capacity and forecasted to provide 30% of the world’s electricity by 2030 [1]. One of the challenges is how to appropriately characterize Wind Power (WP) in the load dispatch model. A conventional economic dispatch problem uses deterministic models, which can not reflect situations considering the WP injection. Since wind farms connected to power systems have characteristics of dynamic and stochastic performance, stochastic models are more suitable. There are several studies intended to investigate the injection of WP into conventional power networks and its impact on the generation resource management due to its stochastic and non-dispatchable characteristics.
A conventional way was to use the average WP. The probabilistic conventional approaches tried to find probabilistic characteristics of solutions of the problem under investigation [2-8]. This approach is called the wait-andsee (WS) strategy in the context of stochastic programming. Although these approaches can be easily implemented, it has a less-known pitfall, called the probabilistic infeasibility. The probabilistic feasibility of the average WP is 0.25, or equivalently, the probabilistic infeasibility is as large as 0.75 [8,9].
For this reason, one of the more appropriate strategies in contrast, the here-and-now (HN) strategy introduces the probabilistic characteristics to the model of optimization problem itself. A here-and-now model of a power system with wind energy generators was developed [10-13]. The authors introduced the stochastic distribution of wind speed into the economic dispatch issue considering both reserve cost of overestimation and penalty cost of underestimation of available wind power. The scheduled wind power output was an estimation value of available wind power output and it was treated as an optimization variable, which was dependent on several factors such as the reserve cost and the penalty cost. But these costs are very difficult to be exactly determined [10].
The probability of stochastic WP is included in the model as a constraint [9,14-17]. This strategy, the hereand-now approach, avoids the probabilistic infeasibility appearing in conventional models and avoids the dependency of the solutions on the reserve cost and the penalty cost. In particular, a threshold parameter pa was introduced into the WP constraint to characterize the tolerance that the total load demand cannot be satisfied. Choosing small pa will mitigate the risk of insufficient WP, while increasing the demand for thermal power.
To analytically remove the assumption that the total WP is characterized by a single random variable, the correlated Weibull distribution (Multivariate Distributions according to Probability Theorems) of the sum of WP is derived from the Weibull distribution model of each WP cluster. This correlated Weibull distribution is used as a chance constraint in the proposed model. With increasing concern over global climate change, policy makers are promoting renewable energy sources, predominantly wind generation, as a means of meeting emissions reduction targets. Although wind generation does not itself produce any harmful emissions, its effect on power system operation can actually cause an increase in the emissions of conventional plants [18]. Thus, the economic dispatch problem can be handled as a multiobjective optimization problem with non-commensurable and contradictory objectives.
In this paper, an EED model is developed for the system consisting of both thermal generators and wind turbines with more realistic and practical considerations. A nondominated sorting genetic algorithm based approach was used for solving the proposed EED model. The problem was formulated as a nonlinear constrained multi-objective optimization problem where fuel cost and environmental impact are treated as competing objectives. Two runs were carried out on a standard test system with non-smooth cost function and the results are analyzed and compared to those of previous works. The effectiveness and potential of the proposed multi-objective EED model are demonstrated.
2. Economic Emission Dispatch Model
The EED problem is to minimize two competing objective functions, fuel cost and emission, while satisfying several equality and inequality constraints. Generally the problem is formulated as follows.
• 2.1. Objective Functions
• Minimization of Fuel Cost:In the past, to solve economic dispatch problem effectively, most algorithms require the incremental cost curves to be of monotonically smooth increasing nature and continuous. The generating units with the multivalve steam turbines exhibit a greater variation by the fuel-cost functions, where the valve point results in the ripple form of the heat-rate curve and the cost function contains higher order nonlinearity due to the valve-point effects, as shown in Figure 1. The more general fuel cost function of each thermal generator considering the valvepoint effect in terms of real power output is expressed as
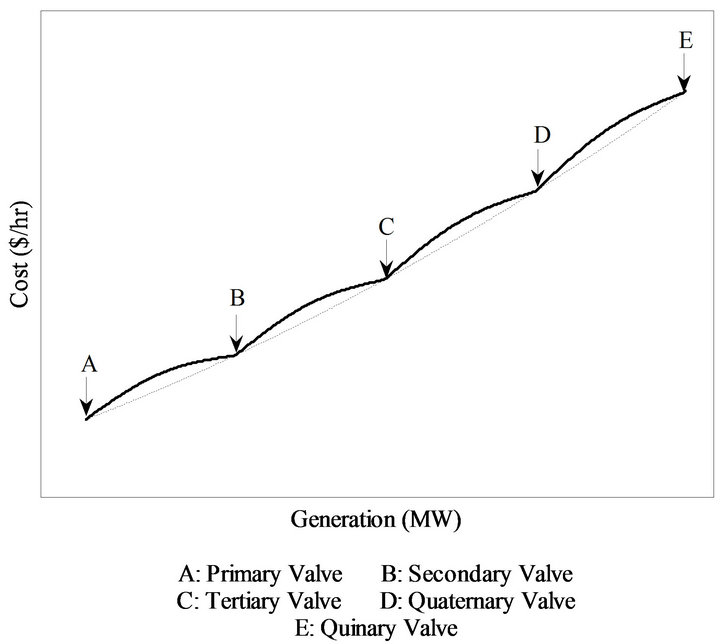
Figure 1. Non-smooth cost function with five valves.
the sum of a quadratic and a sinusoidal function as follow [16]:
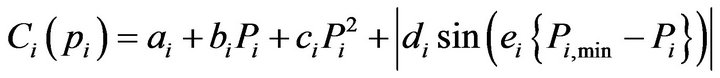 (1)
(1)
The atmospheric pollutants such as sulphur oxides (SOx) and nitrogen oxides (NOx) caused by conventional thermal units can be modeled separately. However the total emission of these pollutants which is the sum of a quadratic and an exponential function can be expressed as [19]:
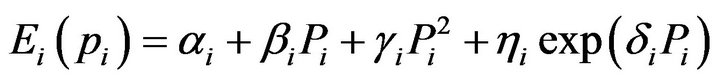 (2)
(2)
2.2. Real Power Operating Limits
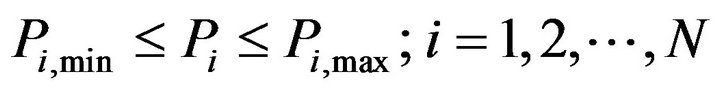 (3)
(3)
2.3. Stochastic Chance Constraint
The power balance constraint is expressed as following:
 (4)
(4)
In chance-constrained programming in the context of stochastic programming, the probability distribution functions of the random variables are used as constraints in the optimization problem. The main goal with chance constraints is, therefore, to determine deterministic equivalents [20]. If the total WP is characterized by a single random variable, the stochastic WP constraint and power balance constraint can be expressed as following [9,14- 16]:
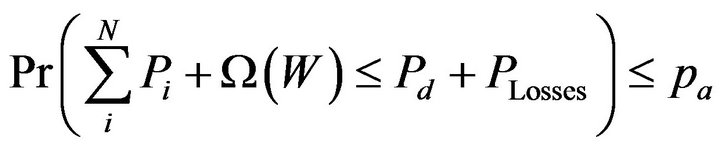 (5)
(5)
In particular, a threshold parameter pa is introduced into the constraint to characterize the tolerance that the total load demand cannot be satisfied [9]. Choosing small pa will mitigate the risk of insufficient WP, while increasing the demand for thermal power. Using Weibull PDF of wind power (5) will be:
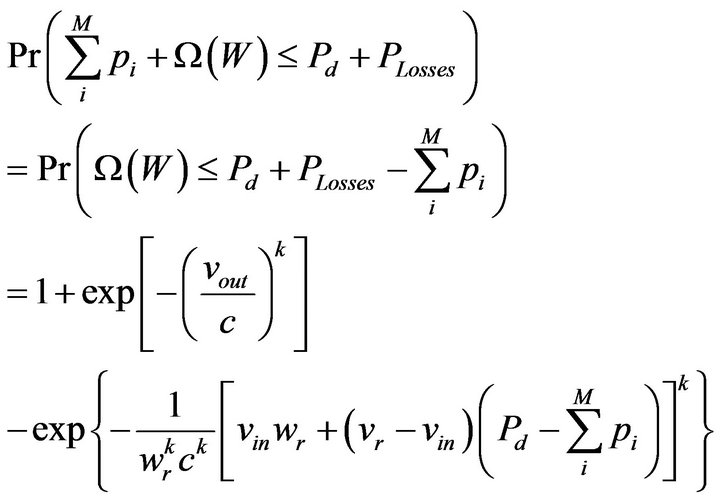 (6)
(6)
This assumes that all wind turbines are located in a coherent geographic area. To analytically remove this assumption, the correlated Weibull distribution is needed. Practically, a large wind farm can be divided into multiple clusters. Hence, from the Weibull distribution model of each cluster, the correlated Weibull distribution of the sum of WP will be derived to be used in proposed models in the next section. For simplification, we only start with two random variables. It implies that we assume that total WP is characterized by two random variables or that wind turbines are located in two different geographic areas.
3. The Correlated Distribution Function
Often an experiment involves measuring two or more random numbers, say X and Y. The fact that we know the distribution of X, and the distribution of Y separately doesn’t determine probabilities of events that involve both X and Y simultaneously [21]. The distribution functions FX(x) and FY(y) of the given random variables determine their separate (marginal) statistics but not joint statistics simultaneously [22].
3.1. Joint Cumulative Distribution and Probability Distribution Functions
The joint (bivariate) cumulative distribution function (CDF) FXY (x, y), or simply, F (x, y) of two random variables X and Y is the probability of the event [22]:
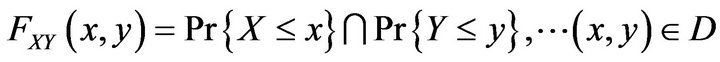 (7)
(7)
The joint probability distribution function (PDF) of X and Y is by definition [22]:
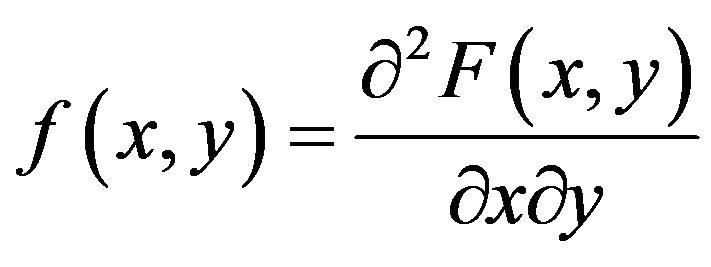 (8)
(8)
3.2. One Function of Two Random Variables
Given two random variables X and Y with Z is the sum of them, we want to find the random variable Z joint statistic probability distributions [21].
The Joint CDF is obtained as following:
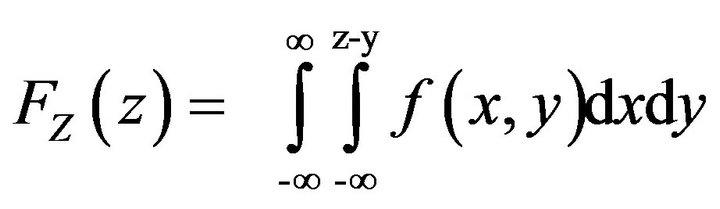 (9)
(9)
And Joint PDF is obtained as following:
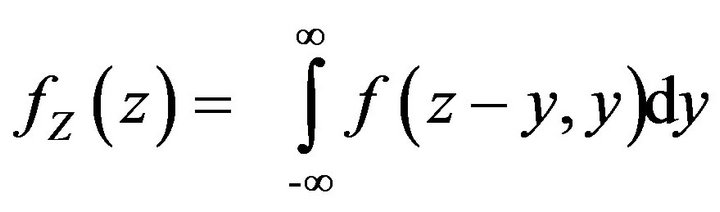 (10)
(10)
Statistically Independent Events and Convolution:
If X and Y are statistically independent then:
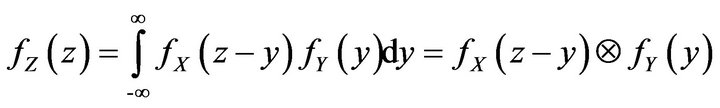 (11)
(11)
where 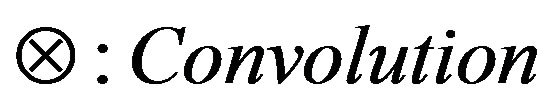
If two random variables are independent, then the PDF of their summation equals the convolution of their PDF [21].
3.3. Bivariate PDF of WP with Two Weibull Random Variables
Since the probability distribution of the WP random variable Wi:
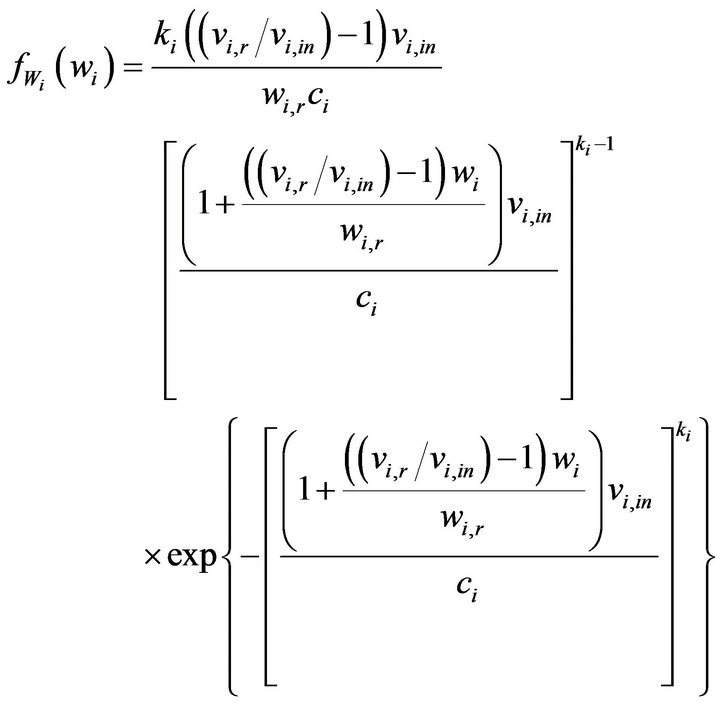 (12)
(12)
Hence the joint statistic probability distributions of random variable W, where W is the sum of two random variables W1 and W2, is:
 (13)
(13)
Then the Stochastic WP Constraint will be:
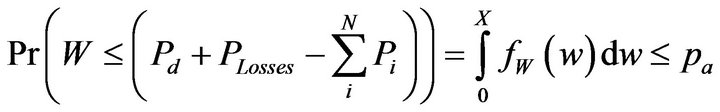 (14)
(14)
where: 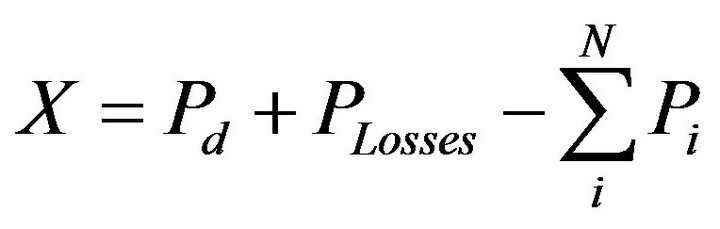
All integrations, differentiations, and convolution operations required in the previous derivation or in the optimization problem solution are executed by using the symbolic MuPAD built in MATLAB.
Hence the economic emission dispatch model can be mathematically formulated as follows:

Subject to: 
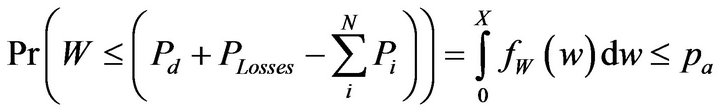
This model, referred to as the here-and-now approach, avoids the probabilistic infeasibility appearing in conventional models and used the derived correlated Weibull distribution of the sum of WP as constraint to avoid the assumption that the total WP is characterized by a single random variable. The transmission losses in terms of B-coefficients in the power balance constraint and more practical cost functions for thermal units were considered in the proposed model.
4. Results and Discussion
The practical EED problems have non-smooth cost functions with equality and inequality constraints in addition to the wind power chance constraint that make the problem of finding the global optimum difficult using any mathematical approaches, so a numerical optimization procedure is needed. In this paper, therefore, we implemented the nondominated sorting multi-objective genetic algorithm in MATLAB to deal with proposed model, the flow chart can be found in the Appendix B [23]. A 69- bus ten-unit test system with non-smooth fuel cost function is used in this paper to demonstrate the performance and the effectiveness of proposed model. Thermal units’ data was taken from [24] and can be found in Appendix C.
Kalyanmoy introduced full details about Multi-objective Genetic Algorithm, but are beyond the scope of discussion here [25]. The proposed model was tested with the 69-bus 10-unit at forecasted load 1800 MW. Threshold parameter pa = 0.4. The Pareto front population fraction was considered in two different cases as follow:
• Case (1) with Pareto front population fraction = 0.7.
• Case (2) with Pareto front population fraction = 0.35.
Figures 2 and 3 show a set of nondominated optimal Pareto solution of the proposed model with Pareto front population fraction 0.7 and 0.35, respectively. As shown in Figures 2 and 3, there is no single solution that is optimal with respect to all objectives of the multi-objective optimization problem. Instead, there is a set of solutions that are superior to the rest of the solutions in the search space considering all objectives. Further, there is no solution in this set is absolutely better than the other solutions. This set is called the Pareto optimal set. It can be seen that the most left side Pareto solution of Figures 2 and 3 gives the Pareto solution of the minimum fuel cost and the most right side Pareto solution of Figures 2 and 3 denotes the Pareto solution of the minimum emission. Also, there is the Pareto solution that means the turning point of a set of optimal Pareto solutions.
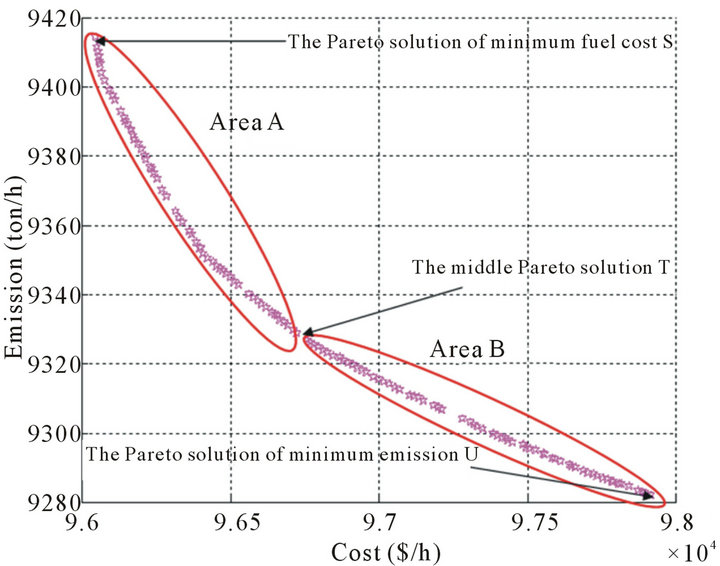
Figure 2. The set of Pareto solutions of the proposed system Case 1.
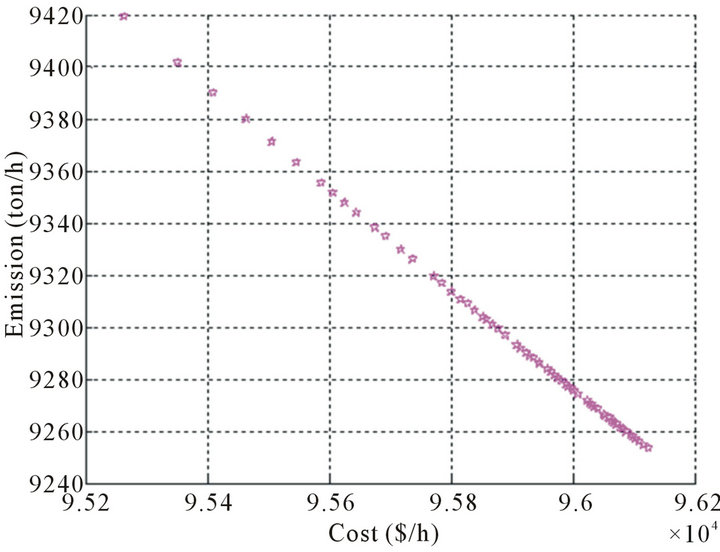
Figure 3. The set of Pareto solutions of the proposed system Case 2.
Area A shows the Pareto solutions that emphasize the economy, while the area B gives the Pareto solutions that emphasize the environmental protection. Table 1 gives values of objective functions and the generators outputs for solutions S, T and U in Figure 2 with Pareto front population fraction 0.7. Table 2 gives values of objective functions and the generators outputs for minimum fuel cost and minimum emission with Pareto front population fraction 0.35 at the most left side and the most right side of Figure 3, respectively.

Table 1. The objective functions and the generators outputs for Case 1.
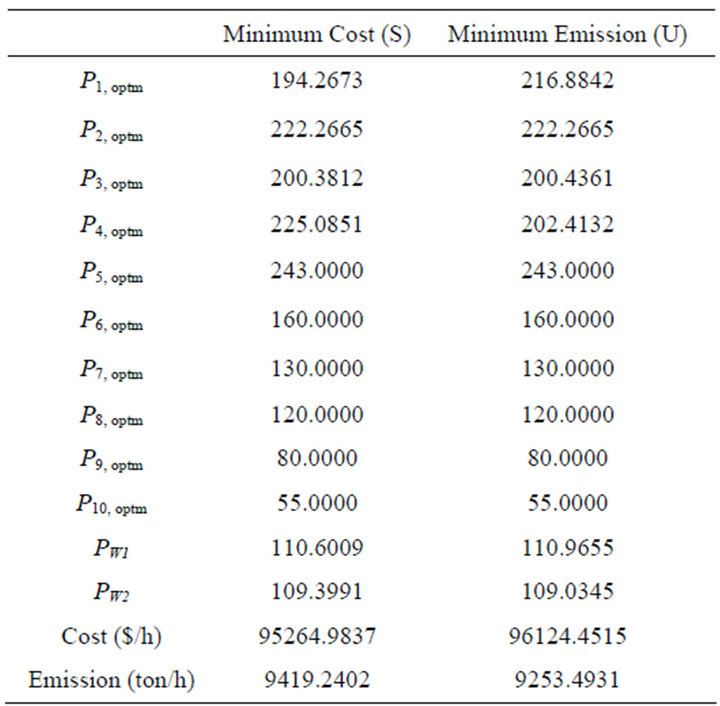
Table 2. The objective functions and the generators outputs for Case 2.
In Figure 2, it can be seen that the Pareto solution of solution U succeeds in reducing 1.42% of amount of emission and degrading 1.95% of the fuel cost in comparison with solution S. In addition, solution T succeeds in reducing 0.93% of amount of emission and degrading 0.71% of the fuel cost in comparison with solution S. Table 1 also shows outputs of generators in Pareto solutions. It can be seen that 1st and 2nd generators have low emission output and high fuel cost because their powers are increasing from solution S to solution T to solution U. Case 1, with Pareto front population fraction 0.7, preserves the diversity of the nondominated solutions over the trade-off front and solve effectively the problem.
The results of the proposed EED model were compared to previous work [15] which obtained the effect of emission constraint and representation of losses. It can be seen that the minimum fuel cost in the proposed model is more than that by Elshahed et al. [15] without considering emission constraint by about 1.9 % and the savings with the proposed model in fuel cost are about 1.4 % when the emission constraint is considered by Elshahed et al. [15]. In addition, the proposed model gives more efficient and noninferior solutions of multi-objective optimization problems.
In contrast with single objective optimization problem found by Elshahed et al. with emission constraint [17], the single solution that is optimal with respect to all objectives of the multi-objective optimization problem does not exist. Instead, there is a set of solutions that is superior to the rest of the solutions in the search space considering cost and emission objectives, so there is no solution in this set is absolutely better than the other solutions. The final decision will be taken by the system dispatchers according to the dispatcher’s attitude. The considered model in this paper achieved saving in minimum fuel cost about 5.8 % when compared with that with single objective function and emission constraint [17]. It can be seen that the wind power results in all solutions are almost constant, because the wind units’ parameters are not changed and also the two units are identical.
5. Conclusions
In this paper, an accurate multi-objective EED model is presented including:
• The transmission losses in terms of B-coefficients• Non-smooth cost functions due to valve-point effect, and
• The correlated Weibull probability distribution of the WP constraint for a system consisting of both thermal generators and wind turbines.
The use of the correlated Weibull probability distribution of the WP analytically removes the assumption that the total WP is characterized by a single random variable in the proposed model. The proposed model minimizes the risk due to uncertainty and can result in minimizing the required spinning reserve. Hence this model is more realistic, practical, and accurate economic emission dispatch model.
In addition, the nondominated solutions in the obtained Pareto-optimal set are well distributed and have satisfactory diversity characteristics which give information regarding the available trade-offs to the system operators. Finally, we can conclude that the proposed EED model provides valuable information and suggestions for safe, reliable, and economic operation of power systems. The results obtained provide direct guidelines for system operators to make correct decisions to schedule the system with WP.
6. Acknowledgements
The authors gratefully acknowledge Dr. Hatem Zeineldin for his guidance and unlimited support during this work.
REFERENCES
- http://www.wwindea.org/home/index.php
- P. Zhang and S. T. Lee, “Probabilistic Load Flow Computation Using the Method of Combined Cumulants and Gram-Charlier Expansion,” IEEE Transactions on Power Systems, Vol. 19, No. 1, 2004, pp. 676-682. doi:10.1109/TPWRS.2003.818743
- A. Schellenberg, W. Rosehart and J. Aguado, “CumulantBased Probabilistic Optimal Power Flow (P-OPF) with Gaussian and Gamma Distributions,” IEEE Transactions on Power Systems, Vol. 20, No. 2, 2005, pp. 773-781. doi:10.1109/TPWRS.2005.846184
- A. Schellenberg, W. Rosehart and J. Aguado, “Introduction to Cumulant-Based Probabilistic Optimal Power Flow (P-OPF),” IEEE Transactions on Power Systems, Vol. 20, No. 2, 2005, pp. 1184-1186. doi:10.1109/TPWRS.2005.846188
- D. Villanueva, A. Feijóo and J. Luis Pazos, “Probabilistic Load Flow Considering Correlation between Generation, Loads and Wind Power,” Smart Grid and Renewable Energy, Vol. 2, No. 1, 2011, pp. 12-20. doi:10.4236/sgre.2011.21002
- Q. Fu, D. C. Yu and J. Ghorai, “Probabilistic Load Flow Analysis for Power Systems with Multi-correlated Wind Source,” Power and Energy Society General Meeting, San Diego, 24-29 July 2011, pp. 1-6. doi:10.1109/PES.2011.6038992
- H. Yang and B. Zou, “The Point Estimate Method Using Third-Order Polynomial Normal Transformation Technique to Solve Probabilistic Power Flow With Correlated Wind Source and Load,” Asia-Pacific Power and Energy Engineering Conference (APPEEC), Shanghai, 27-29 March 2012, pp. 1-4. doi:10.1109/APPEEC.2012.6307479
- X. Liu, “Economic Load Dispatch Constrained by Wind Power Availability: A Wait-and-See Approach,” IEEE Transactions on Smart Grid, Vol. 1, No. 3, 2010, pp. 347- 355. dio:10.1109/TSG.2010.2057458
- X. Liu and W. Xu, “Economic Load Dispatch Constrained by WP Availability: A Here-and-Now Approach,” IEEE Transactions on Sustainable Energy, Vol. 1, No. 1, 2010, pp. 2-9. doi:10.1109/TSTE.2010.2044817
- J. Hetzer and D. C. Yu, “An Economic Dispatch Model Incorporating Wind Power,” IEEE Transactions on Energy Conversion, Vol. 23, No. 2, 2008, pp. 603-611. doi:10.1109/TEC.2007.914171
- D. Villanueva, A. Feijóo and J. Pazos, “Simulation of Correlated Wind Speed Data for Economic Dispatch Evaluation,” IEEE Transactions on Sustainable Energy, Vol. 3, No. 1, 2012, pp. 142-149. doi:10.1109/TSTE.2011.2165861
- Y. Fang, D. Zhao, M. Ke, X. Zhao, C. Herbert and K. Wong, “Quantum-Inspired Particle Swarm Optimization for Power System Operations Considering Wind Power Uncertainty and Carbon Tax in Australia,” IEEE Transactions on Industrial Informatics, Vol. 8, No. 4, 2012, pp. 880-888. doi:10.1109/TII.2012.2210431
- G. S. Piperagkas, A. G. Anastasiadis and N. D. Hatziargyriou, “Stochastic PSO-Based Heat and Power Dispatch under Environmental Constraints Incorporating CHP and Wind Power Units,” Electric Power Systems Research, Vol. 81, No. 1, 2011, pp. 209-218. doi:10.1016/j.epsr.2010.08.009
- X. Liu, W. Xu and C. C. Huang, “Economic Load Dispatch with Stochastic Wind Power: Model and Solutions,” Transmission and Distribution Conference and Exposition, New Orleans, 19-22 April 2010, pp. 1-7. doi:10.1109/TDC.2010.5484550
- M. Elshahed, M. Elmarsfawy and H. Zeineldin, “A Here-and-Now Stochastic Economic Dispatch with NonSmooth Fuel Cost Function and Emission Constraint,” The Online Journal on Electronics and Electrical Engineering (OJEEE), Vol. 3, No. 4, 2011, pp. 484-489.
- M. Elshahed, M. Elmarsfawy and H. Zeineldin, “Dynamic Economic Dispatch Constrained by Wind Power Weibull Distribution: A Here-and-Now Strategy,” World Academy of Science, Engineering and Technology Journal, Vol. 56, 2011, pp. 384-389.
- M. Elshahed, M. Elmarsfawy and H. Zeineldin, “A New Economic Dispatch Constrained by Correlated Weibull Probability Distribution Model for Wind Power,” IEEE PES Conference on Innovative Smart Grid TechnologiesME, Jeddah, 17-20 December 2011, pp. 1-6. doi:10.1109/ISGT-MidEast.2011.6220811
- X. Liu and W. Xu, “Minimum Emission Dispatch Constrained by Stochastic Wind Power Availability and Cost,” IEEE Transactions on Power Systems, Vol. 25, No. 3, 2010, pp. 1705-1713. doi:10.1109/TPWRS.2010.2042085
- M. A. Abido, “Environmental/Economic Power Dispatch Using Multi-Objective Evolutionary Algorithms,” IEEE Transactions on Power Systems, Vol. 18, No. 4, 2003, pp. 1529-1537. doi:10.1109/TPWRS.2003.818693
- J. R. Birge and F. Louveaux, “Introduction to Stochastic Programming,” 2nd Edition, Springer, Berlin, 2011.
- M. Lefebvre, “Applied Stochastic Processes,” Springer Inc., Berlin, 2007.
- A. Papoulis, “Probability, Random Variables and Stochastic Processes,” 3rd Edition, McGraw-Hill Inc., Boston, 1991.
- T. A. Saafan, S. H. Moharram, M. I. Gad and S. K. Allah, “A Multi-Objective Optimization Approach to Groundwater Management Using Genetic Algorithm,” International Journal of Water Resources and Environmental Engineering, Vol. 3, No. 7, 2011, pp. 139-149.
- M. Basu, “Dynamic Economic Emission Dispatch Using Non-Dominated Sorting Genetic Algorithm-II,” Electrical Power and Energy Systems Journal, Vol. 30, No. 2, 2008, pp. 140-149. doi:10.1016/j.ijepes.2007.06.009
- K. Deb, “Multi-Objective Optimization Using Evolutionary Algorithms,” John Wiley & Sons, Ltd., Chichester, 2001.
Appendix A
Nomenclatures
ai, bi, ci, di, and ei: Cost coefficients of ith unit
αi, βi, γi, ηi, δi: Emission coefficients of ith unit c: Scale factor of the Weibull distribution k: Shape factor of the Weibull distribution N: Number of Thermal generators Pi,min and Pi,max: Min and Max power generated by generator i Pi: Real power generated by generator i Pd: Total Load Demand PLosses: Transmission System Losses Pr (E): Probability of event E Pd: Total Load Demand PLosses: Transmission System Losses pa: specified threshold representing the tolerance that the total demand cannot be satisfied.
vr, vin, and vout: Rated, cut-in, and cut-out wind speeds W: Real power generated by wind farm wr: Rated wind power W(W): a Weibull PDF functional of random variable W
Appendix B
The flowchart of the multi-objective genetic algorithm used in this paper is shown in Figure 4.
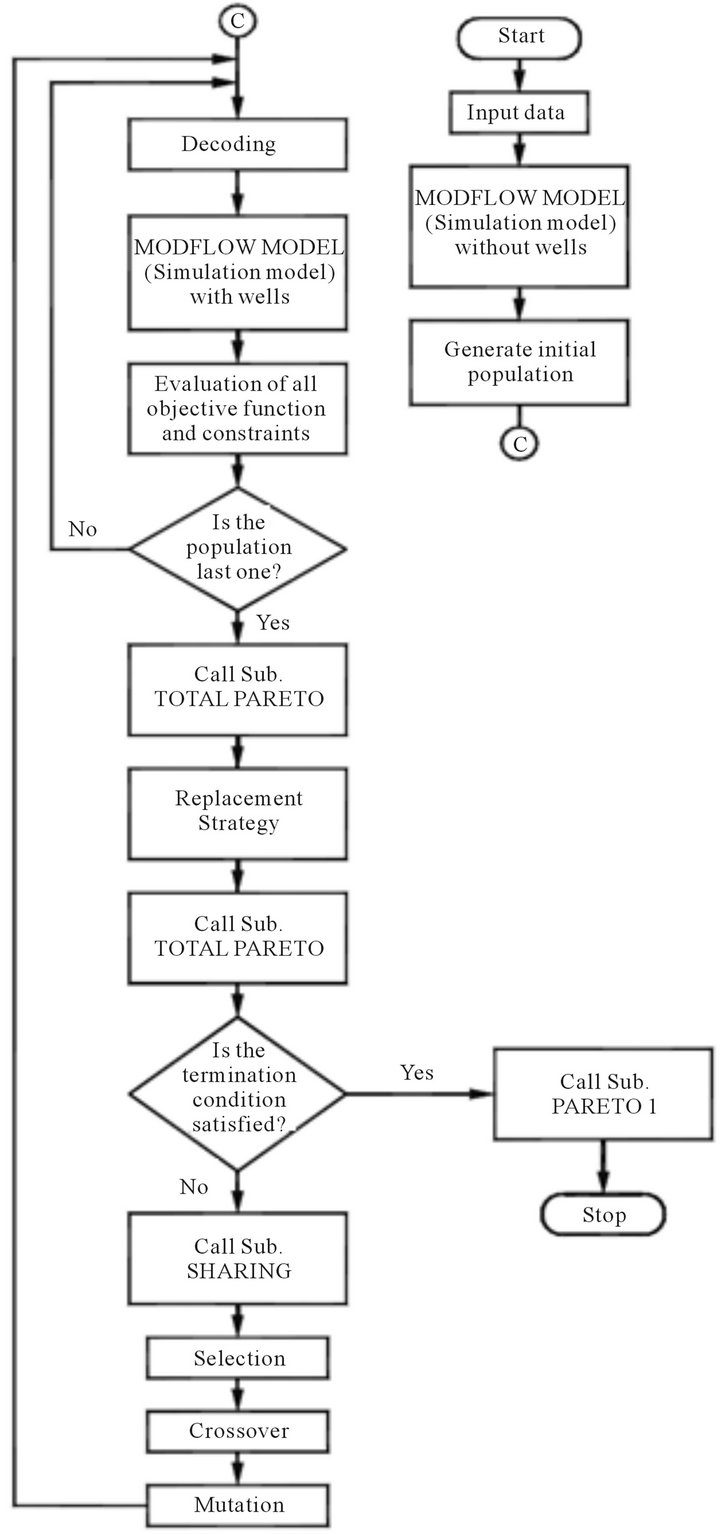
Figure 4. Flowchart of the multi-objective genetic algorithm.
Appendix C
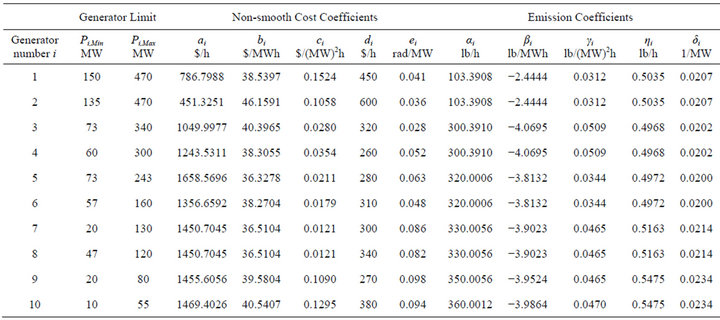
Table C1.Conventional generators characteristics.
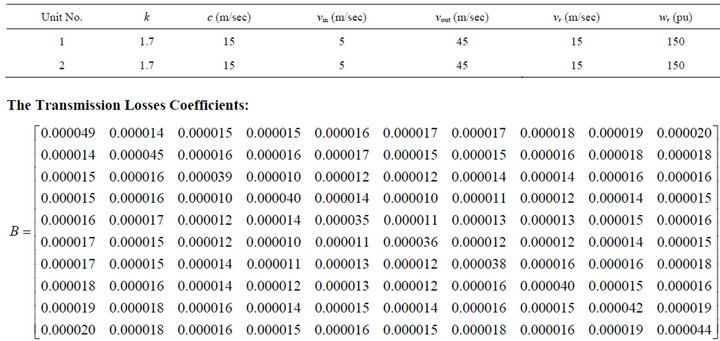
Table C2.Two wind units parameters.

