Smart Grid and Renewable Energy
Vol.4 No.3(2013), Article ID:33029,7 pages DOI:10.4236/sgre.2012.43031
Design and Development of a Wind Turbine Simulator Using a Separately Excited DC Motor
![]()
Department of Electrical Engineering, University of Moratuwa, Katubedda, Sri Lanka.
Email: udayanga@elect.mrt.ac.lk
Copyright © 2013 K. K. M. S. Kariyawasam et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 16th, 2012; revised March 5th, 2013; accepted March 14th, 2013
Keywords: Wind Turbines; Wind Turbine Simulator; PI Controller; Variable Load; Microgrid
ABSTRACT
Over the course of the past decade, power generation based on wind energy has become a significant component in modern power systems, which has caused substantial increase in the wind power based research. As it is complicated to use a real wind turbine for laboratory purposes, development of a replica of a real wind turbine that can be connected and used indoors is imperative. This paper presents the design and development of a wind turbine simulator that operates on the typical power-speed characteristics of a wind turbine. First, the mathematical model of the wind turbine simulator is developed and the corresponding CAD simulations are carried out. Proposed hardware implementations involve a DC motor-DC generator set, a variable load and a control system based on PI controllers. It is a simple, low power and low cost design that can be easily connected to an AC system through an inverter.
1. Introduction
Wind energy is one of the major sources of alternate energy, which has the potential to cater for the diminishing fossil fuels. The total installed capacity of wind energy based power generation in the world has seen a tenfold increase in the past decade alone. Up and coming concepts such as microgrids and smartgrids have added further value to wind power generation, in which Distributed Generation (DG) units such as small roof-top wind turbines are accommodated.
1.1. Wind Turbines
Wind turbines are mechanical devices designed to convert the kinetic energy of the wind into useful mechanical energy that can be later converted into electricity. In general, commercial grid connected wind turbines can be classified into two categories as variable pitch and fixed pitch wind turbines. Mechanical torque and power produced by a wind turbine are functions of the pitch angle, β, and the tip speed ratio, λ (the ratio between the speed of the blade tip and the velocity of wind). For a fixed pitch wind turbine (where pitch angle is naturally zero), it can be shown that mechanical torque and power are functions of rotational speed of the rotor only (for a given wind speed), as shown in Figure 1. These characteristics will be further discussed in Section 2.
1.2. Wind Turbine Simulators
With the rapid increase of wind power installations, research related to wind energy systems is also boomed. As a result, a device that can mimic the functionality of a wind turbine in a laboratory environment is of utter importance. The foremost requirement of such a device, which may be called a wind turbine simulator, is the ability to produce the same static and dynamic characteristics of a real wind turbine [1].
There are several types of wind turbine simulators developed employing different kinds of motors and control techniques. DC motors, induction motors and although rarely, synchronous motors are being used as the prime mover of these wind turbine simulators. Wind turbine simulators using DC motors (separately exited) often use armature and field voltage control methods to achieve static characteristics of a fixed pitch wind turbine [2]. These simulators are simple, uncomplicated and usually do not consider the transient operations. On the other hand, there are several simulators consisting of three phase induction motors with torque control invertors, which are capable of accounting for transient distur-

Figure 1. Power output vs. Rotor speed characteristic of a wind turbine for different wind speeds.
bances such as the tower effect [2]. In some simulators permanent magnet synchronous motors are used as the prime mover with a voltage sourced converter.
Similar to the prime movers, there are many types of generators used in different wind turbine simulators. Induction generators are the most common with the occasional use of synchronous and DC generators [3,4].
Although not very popular in modern era, wind systems having a wind turbine connected to a DC generator and a battery bank were used in small scale wind topologies [5]. However, with so much attention on distributed generation and integration of renewable energies becoming indispensable, these small scale wind turbines come into the picture again. The objective of this work is to simulate a small scale wind energy system that can be connected to a microgrid. Here, at the initial stage, only the isolated operation of a wind turbine coupled to a DC generator, connected to resistive load is considered.
2. Mathematical Analysis and Modeling
Wind turbines are capable of capturing the kinetic energy of the wind and transfer it into an electrical generator. Some of the wind turbines are coupled with the generator through a gear set but many turbines are directly coupled to low speed generators without a gear set to minimize the losses [1].
2.1. Power Output of a Wind Turbine
The total amount of energy extractable from a wind turbine can be calculated theoretically, using translational momentum theory [6]. Power extractable from the wind passing across an area A, when the wind speed is v can be expressed as,
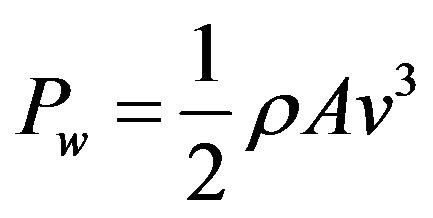 (1)
(1)
Here, ρ is the density of air, which depends on the pressure and moisture levels of air. Betz’s law states that the maximum fraction of power extracted by a wind turbine would be theoretically 16/27 of Pw. However in practice, turbines would extract a significantly lesser portion of wind power. Even modern commercial wind turbines extract about 0.45 of Pw [7]. Thus, a coefficient is defined to express the useful mechanical power extracted from the wind by the turbine. It is called the power coefficient or the Betz factor, cp, and defined as,
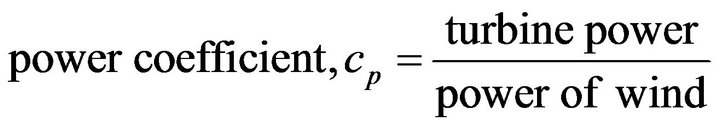 (2)
(2)
Power coefficient, cp, is a function of two variables, namely, tip speed ratio, λ, and pitch angle, β. Tip speed ratio, λ, is the ratio between the speed of the tip of the blade, ωR, and the velocity of wind, v. Here, ω is the rotational speed of the turbine rotor and R is the radius of the turbine blade.
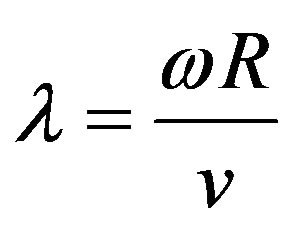 (3)
(3)
Moreover, cp is also a function of the pitch angle, β but for a fixed pitch wind turbine, β, is generally zero [7]. Then the turbine power extracted by a fixed pitch wind turbine can be expressed as,
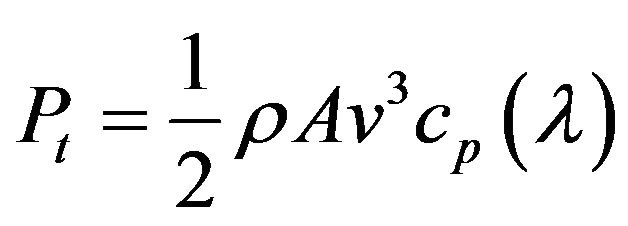 (4)
(4)
In Equation (4), the circular swept area of the turbine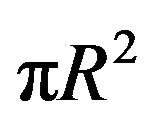 is given as A [6]. Further it can be seen that for a given wind speed, tip speed ratio, λ, is a function of ω only and hence, cp becomes a function of ω only. Therefore, the power extracted by a fixed pitch wind turbine, Pt, is a function of its rotor speed, ω, only, provided that the wind speed remains constant.
is given as A [6]. Further it can be seen that for a given wind speed, tip speed ratio, λ, is a function of ω only and hence, cp becomes a function of ω only. Therefore, the power extracted by a fixed pitch wind turbine, Pt, is a function of its rotor speed, ω, only, provided that the wind speed remains constant.
Similarly, a coefficient can be defined for the torque extracted as ct, and the torque output of a fixed pitch wind turbine can be given as,
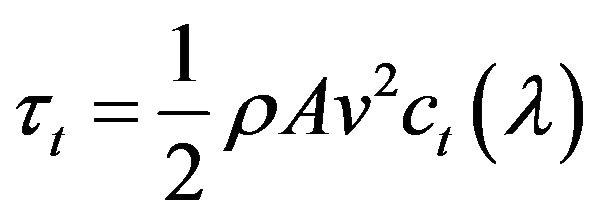 (5)
(5)
Torque of the turbine can also be expressed as,
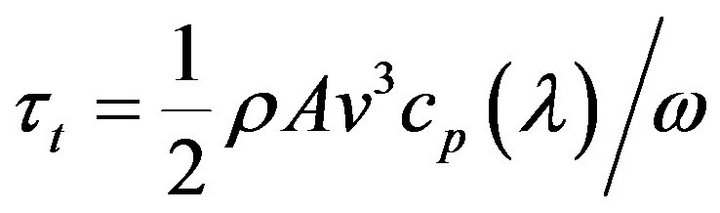 (6)
(6)
Furthermore,
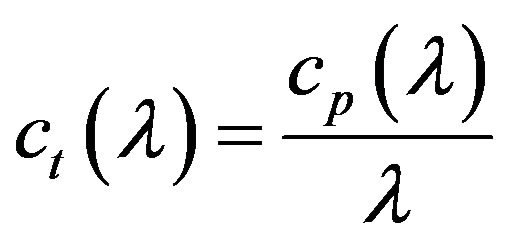 (7)
(7)
2.2. Modeling of the DC Motor-DC Generator Couple
In the following analysis, a mathematical model is developed for a DC motor and a DC generator, which are directly coupled by a horizontal shaft and a resistive load is connected at the generator end.
Using KVL (Kirchhoff’s Voltage Law) and basic rotational motion equations, a model can be developed for the above mentioned system. Applying KVL to the motor circuit, we can obtain,
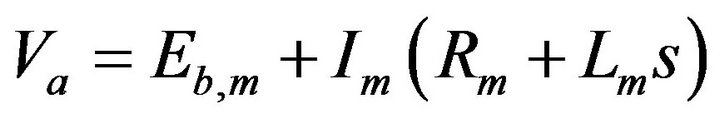 (8)
(8)
Here, Va is the motor armature resistance, Eb,m is the back emf of the motor, Im is the motor armature current, Rm is the armature resistance of the motor and Lm is the armature inductance of the motor. Similarly, from the generator circuit we can get,
 (9)
(9)
DC generator also has corresponding parameters similar to those mentioned above, which are being indicated with the subscript g, except for Eg, which now is the induced emf in the generator rather than a back emf. Furthermore, considering the mechanical subsystem, we can write,
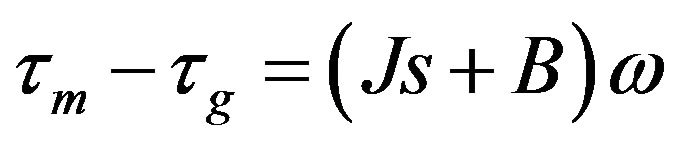 (10)
(10)
Here, τm and τg are motor and generator electrical torques respectively.
And J is the total system inertia and B is the damping constant. ω is the angular speed of the system. Frictional torque is neglected in this analysis. Then, for the DC motor we can write,
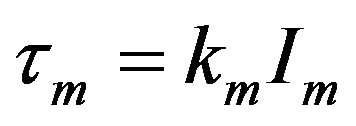 (11)
(11)
And,
 (12)
(12)
Here, torque constant and voltage constant of the motor are assumed to be equal and denoted by km as the motor constant. Corresponding equations can be written for the generator as,
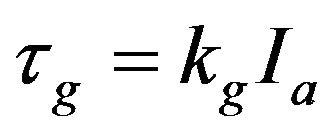 (13)
(13)
And,
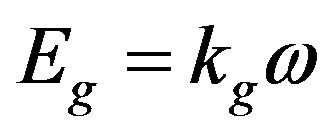 (14)
(14)
Moreover, in this analysis, armature reaction is not taken into consideration. By combining and rearranging above equations, the closed loop system shown in Figure 2 can be obtained.
Further, two PI controller transfer function blocks are also included. There, KP,ω and KI,ω are the proportional and integral gains of the PI controller governing the speed where as KP,P and KI,P are the proportional and integral gains of the PI controller governing the power output. Output of the speed governing controller is directly proportional to the armature voltage of the motor, while the Output of the PI controller governing the power output varies the load resistance connected to the generator and thereby, controls the power output. The block 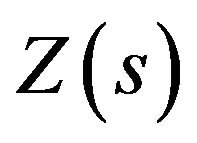 represents a subsystem, where two resistors (R1 and R2) are connected in parallel (to the generator terminals) and the effective value of one of them (say R2) is varied by switching it on and off using a PWM signal. If the duty ratio of the PWM switching signal is taken as D,
represents a subsystem, where two resistors (R1 and R2) are connected in parallel (to the generator terminals) and the effective value of one of them (say R2) is varied by switching it on and off using a PWM signal. If the duty ratio of the PWM switching signal is taken as D,  can be written as,
can be written as,
 (15)
(15)
2.3. Load Model
Let’s consider a purely resistive load connected to a DC generator output terminals. Equation (9) is again applicable.
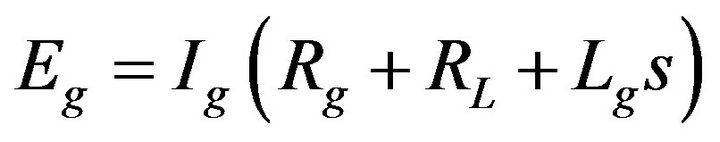
At steady state, this becomes,
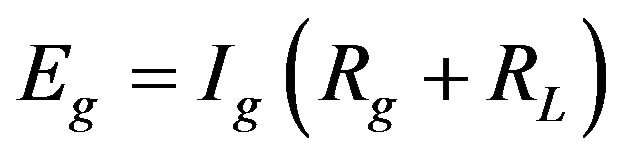 (16)
(16)
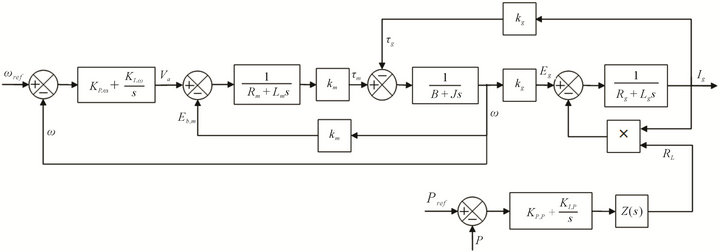
Figure 2. Closed loop control diagram of the system.
Using Equations (14) and (16), we can express the steady state current flowing through the load as,
 (17)
(17)
where, RL is the value of the resistive load. Further, the power consumption of the resistive load, PL, is given by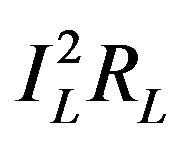 , when a current of IL flows through it and the substitution of IL from Equation (17) would yield,
, when a current of IL flows through it and the substitution of IL from Equation (17) would yield,
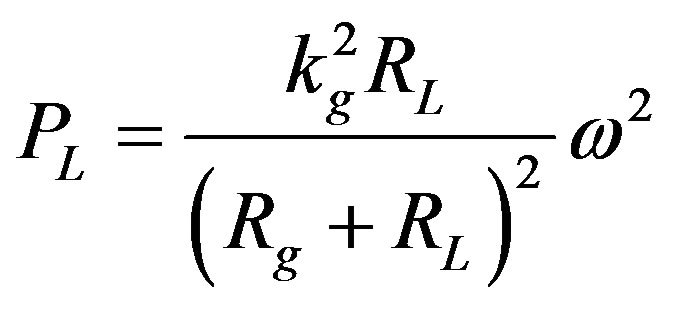 (18)
(18)
From Equation (18), it can be seen that for a given resistive value, PL is a quadratic function of ω.
The curve described by Equation (18), along with the power vs. rotor speed characteristic of the wind turbine would determine the operating point of the system on the power-speed (P-ω) plane. In other words, the intersection point of the two curves on P-ω plane would be operating point of the system for a given wind speed and a given resistor value. In this analysis, power losses between the turbine shaft and the generator output terminals are neglected.
These theoretical operating points provide the necessary reference values (two references, a speed reference and a power reference) for the controllers of the system.
Figure 3 illustrates the turbine power output curves (blue) and the load curves (red) and their intersection points on the P-ω plane. Here, the equation of the wind turbine characteristic curve is obtained based on work done in [8]. Further, plots are being rescaled so that they are in the working region of the motor-generator couple used.
3. Control Mechanism
Two independent PI controllers are used to get the sys-
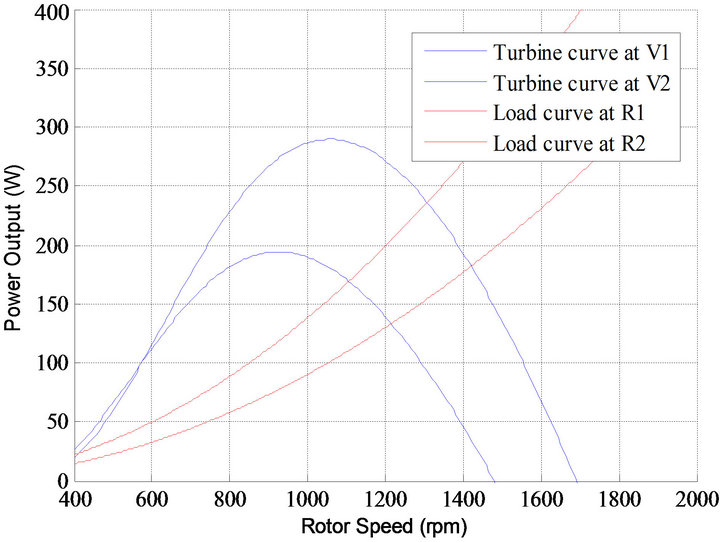
Figure 3. Wind turbine curves and load curves.
tem operating point converged on to the desired reference point on the P-ω plane. One of them governs the rotor speed of the motor-generator couple, while the other governs the power output of the generator.
3.1. PI Controller Governing the Rotor Speed
Once the wind speed and the load resistance are specified, the corresponding system operating point can be determined, which provides the controlling circuit with two references, namely, a speed reference and a power reference. As illustrated in Figure 4, the speed reference is fed to the speed controlling PI controller, which adjusts the armature voltage of the motor to obtain an acceptable response.
3.2. PI Controller Governing the Power Output
As mentioned above, determination of the operating point of the system provides a second reference, the power output of the turbine. Considering measuring difficulties, the shaft power output of the DC motor (which otherwise should have been the corresponding parameter for the wind turbine power output) is assumed to be equal to the power output of the DC generator.
The PI controller generates a signal that varies the resistor value of the load and by so doing, controls the generator loading, as shown in Figure 5. The variable resistor has a resistance value that can vary approximately between 100 - 400 Ω, according to the duty ratio of the switching signal. Load control will be further detailed under hardware implementations.
4. Simulations
To validate the theoretical design developed, simulations were carried out employing CAD software packages. Firstly, the closed loop control system of the design (shown in Figure 2), with PI controllers, was imple-
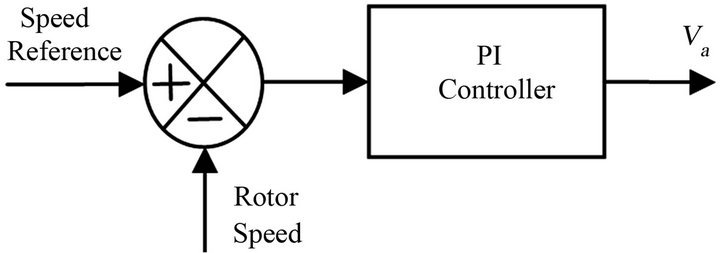
Figure 4. PI controller governing the rotor speed.
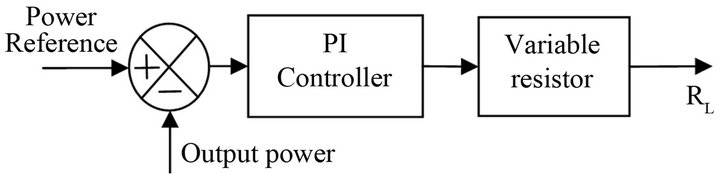
Figure 5. PI controller governing the generator power output.
mented using a dynamic system modeling software package (MATLAB Simulink). This simulation only contains the mathematical design of the proposed design (using only transfer function type blocks, not inbuilt Simulink models such as Simulink DC motor model). Results obtained from that simulation verified the theoretical basis of our design, thus, it was decided to simulate the system in an environment that is closer to the real world. Then, using an electromagnetic transient (EMT) type software package (PSCAD/EMTDC), system design was again simulated and got appreciably satisfactory results. Here, inbuilt models of the software package were employed and the circuit diagram of PSCAD/EMTDC simulation is shown in Figure 6.
As shown in Figure 6, DC motor and DC generator are directly coupled and the field voltages of the two machines are kept constant. The effective armature voltage of the motor is controlled by a PWM switching signal driven power electronic device. The duty ratio of the PWM switching signal is created according to the PI controller output. Similarly, the output terminals of the DC generator are connected to two resistors in parallel, one 400 Ω and the other 125 Ω. The later resister is switched thorough a power electronic device, whose switching signal is created according to the output of the respective PI controller. By so doing, the total effective load on the generator is varied and the operating point of the system can be altered. Using these two controls, working in tandem, the system operating can be converged onto the desired point on the P-ω plane.
The inputs of the system, as indicated in Figure 6, are the wind speed and load resistance. For each set of wind speed and load resistance, there is a corresponding system operating point (as explained in Section 2.3), thus, a speed reference and a power reference. These data is pre-calculated and stored in a data file as look up tables and once a set of wind speed and load resistance is inserted, the program can access the tables and find the respective references, which are then being fed to the two PI controllers.
After getting the initial results satisfactorily, control system optimization procedures were carried out. Optimization of the control system refers to the optimization of the two PI controllers or in other words, finding the optimal values for proportional and integral gains of the controllers and thus, produce an appreciable response for both rotor speed and power output. To accomplish this, the embedded optimization blocks in PSCAD/EMTDC were used (simplex optimum run).
5. Hardware Implementation
The basic arrangement of hardware design is shown in Figures 7 and 8. Here, a provided wind profile is fed to the control circuit via a computer interface (GUI). Accordingly the control circuit decides the set point of the wind turbine (assuming that the load connected remains constant; if required, value of the load resistor can also be changed via computer interface) and then varies the armature voltage of the DC motor and the resistive load connected to the DC generator to achieve the specified point on the power-speed plane. Rated voltage of the both the DC machines are 220 V and power associated with this model is below 0.5 kW. Control circuit implementations are microcontroller based. Since it is difficult to measure the torque or the power transferred from the motor to generator, electrical power output of the generator is considered. An encoder with a U sensor is used to measure the rotor speed of the couple. Variable load is made out of Nichrome coils. The control mechanism is based on PI controllers and the two independent PI controllers are implemented to govern speed and power.
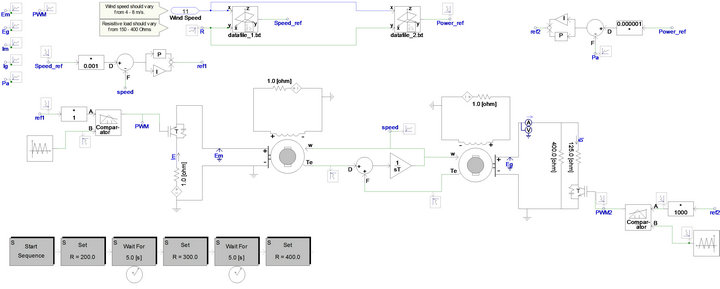
Figure 6. Circuit diagram of PSCAD/EMTDC simulation.
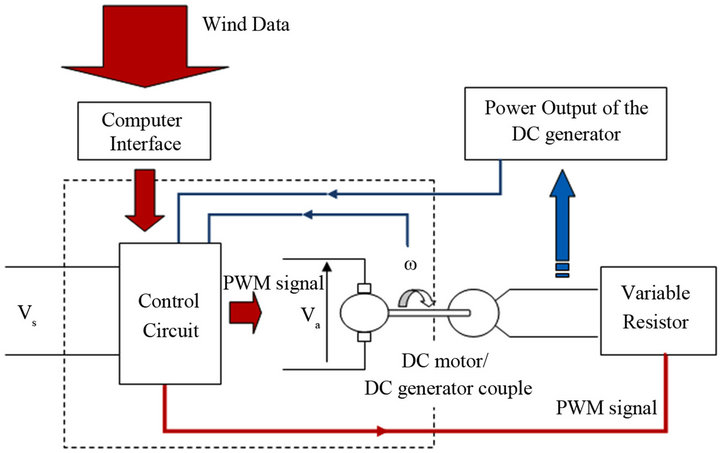
Figure 7. Hardware apparatus.

Figure 8. Hardware implementations.
Once the wind speed and the external load status are fed into the system, the control circuit determines the speed reference and the power reference using look up tables. The PI controller governing the speed of the couple tracks the speed error and accordingly, varies the duty ratio of the PWM switching signal of the power electronic switching device that drives the motor. Similarly, the corresponding power controller tracks the power error and adjusts the PWM switching signal of the power electronic switching device that connects the load to the generator (thus controls the power flow).
As mentioned above, the output terminals of the DC generator are connected to two resistors in parallel, one 400 Ω and other 125 Ω. By switching the 125 Ω resistor thorough a power electronic device, the total resistance on the generator can be varied approximately between 100 - 400 Ω, which is designed to comply the machines ratings.
6. Simulation Results
Simulation work was carried out, in both MATLAB Simulink and PSCAD/EMTDC and satisfactory results were obtained.
Simulations were carried out in two different levels on two different software packages. The theoretical system was simulated in MATLAB Simulink, while a more hardware based simulation was carried out in PSCAD/ EMTDC.
Figure 9 clearly illustrates the system operating points being on the theoretical P-ω curve of the wind turbine, thus, verifying the validity of the theoretical analysis carried out.
The optimum run produced the proportional gain, Kp, of the speed controlling PI controller as 10.0528 and the integral gain, Ki, as 0.0431329. Corresponding constants for the PI controller governing the power output were 25.0366 and 0.0121125, respectively.
From Figures 10 and 11 results, it can be seen that though the speed response of the system was not largely affected by optimization, power response was greatly enhanced by it.
7. Future Work and Conclusions
A variable speed fixed pitch wind turbine connected to a

Figure 9. Operating points obtained from MATLAB simulink and PSCAD/EMTDC simulations plotted with the theoretical wind turbine characteristic curves for various wind speeds.
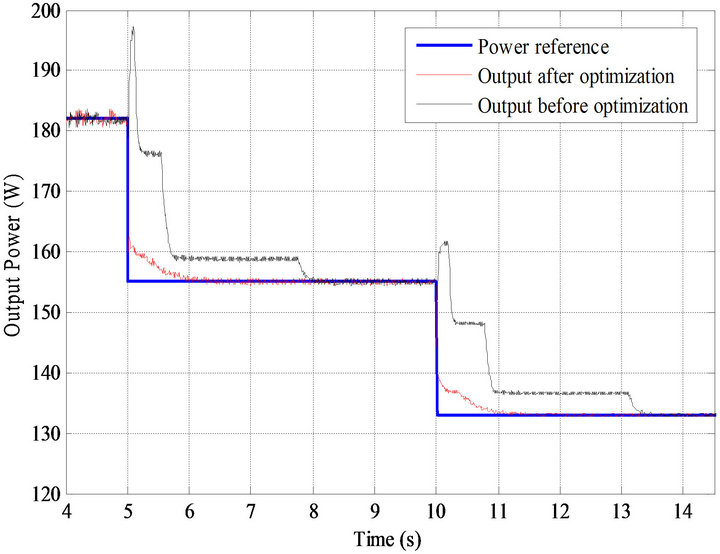
Figure 10. Power reference plotted with the power output response of the system before and after optimization carried out in PSCAD/EMTDC.
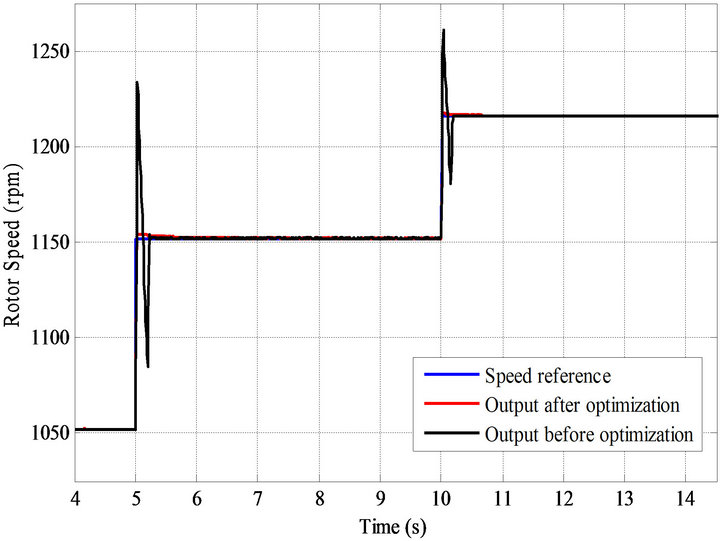
Figure 11. Speed reference plotted with the speed output response of the system before and after optimization carried out in PSCAD/EMTDC.
DC generator, working on isolated operation is simulated in order to evaluate the potential of integrating small household wind turbines into microgrids. In the suggested simulator, wind turbine is emulated using a DC motor. A combination of wind profiles and load conditions are emulated. Control algorithms are based on PI controllers and implemented using microcontrollers. Simulations are carried out in both MATLAB simulink and PSCAD/EMTDC. Simulations results comply with the theoretical analysis, validating the system model.
In future, hardware implementations are to be completed and further analysis regarding the characteristics of the wind turbine would be carried out. Next phase of this work is to design and implement an inverter that can integrate the wind turbine simulator into a microgrid testbed.
REFERENCES
- H. M. Kojabadi, C. Liuchen and T. Boutot, “Development of a Novel Wind Turbine Simulator for Wind Energy Conversion Systems Using an Inverter-Controlled Induction Motor,” IEEE Transactions on Energy Conversion, Vol. 19, No. 3, 2004, pp. 547-552. doi:10.1109/TEC.2004.832070
- F. Martinez, S. de Pablo and L. C. Herrero, “Fixed Pitch Wind Turbine Emulator Using a DC Motor and a Series Resistor,” Power Electronics and Applications (EPE’09), Barcelona , 8-10 September 2009
- N. Bunlung, S. Sirisumrannukul and S. Chatratana, “Development of a Wind Turbine Simulator for Wind Generator Testing,” International Energy Journal, Vol. 8, No. 1, 2007, pp. 21-28.
- D. S. L. Dolan and P. W. Lehn, “Real-Time Wind Turbine Emulator Suitable for Power Quality and Dynamic Control Studies,” International Conference on Power Systems Transients, Montreal, 19-23 June 2005.
- G. L. Johnson, “Wind Energy Systems,” Prentice Hall, 1985.
- M. Stiebler, “Wind Energy Systems for Electric Power Generation (Green Energy & Technology),” Springer, 2008.
- F. D. Bianchi, H. De Battista and R. Mantz, “Wind Turbine Control Systems: Principles, Modeling and Gain Scheduling Design,” Springer, 2006.
- J. G. Slootweg, S. W. H. de Haan, H. Polinder and W. L. Kling, “General Model for Representing Variable Speed Wind Turbines in Power System Dynamics Simulations,” IEEE Transactions on Power Systems, Vol. 18, No. 1, 2003, pp. 144-151.

