ABSTRACT

As rapid economic growth in China in recent decades, the quality of economic growth through improvement of energy efficiency has attracted great attention. This paper evaluated energy efficiency of 29 provinces in China between 2000 and 2016 based on a global non-radial directional distance function. Moreover, the dynamics of energy efficiency were investigated using the non-radial global Malmquist-type efficiency index. The paper also sheds light on the evolution of inequalities in energy efficiency by decomposing interprovincial inequality into its within-region and between-region components. The findings of the study are as follows. First, the national energy efficiency was 0.49 in 2016, which indicated that 51% improvement could be made to reach the global technology frontier. Tianjin, Shanghai, Jiangsu, Shandong and Guangdong had the best energy efficiency in 2016, while Ningxia and Xinjiang had the lowest performance. Second, the national annual growth rate of energy efficiency was 3.4% between 2011 and 2016, which was a positive sign of energy efficiency improvement. Shandong made the biggest improvement in energy efficiency from 2011 to 2016, with 26.2% annual growth rate. Lastly, within-region inequality saw a decreasing trend after 2010 and was overtaken by between-region inequality in 2016.

Keywords:

Non-Radial Directional Distance Function, Energy Efficiency, Inequality, Dynamics

1. Introduction

As China has experienced a rapid economic increase in recent decades, about 23.4% primary energy consumption comes from China, more than the United States (16.5%) and the total Europe (14.6%) in 2017 [1] . Rapid economic growth has led to an increasing GDP and better living conditions. In addition, it has caused rapid increase in energy consumption. According to Chinese Statistical Yearbooks, China’s energy consumption also rose dramatically, from 1385.70 million metric tce in 2000 to 3590.00 million tce in 2017. The large amount of energy consumption has caused rapid rise in CO₂ emissions and further contributed to global warming. Therefore, China’s government has set some targets to promote sustainable development and has paid great attention to energy saving and CO₂ emissions mitigation. China has set a target of reducing carbon intensity by 40% - 45% by 2020, compared to 2005 levels, and increasing the proportion of non-fossil fuels in primary energy consumption to around 15% [2] . Therefore, to realize the mitigation goal, more attention should be paid on the quality of economic growth through improvement of energy efficiency.

Energy efficiency has been widely measured by energy intensity [3] [4] [5] . However, energy intensity is not able to fully demonstrate the total-factor production process. Therefore, these indexes can be regarded as the partial-factor energy performances analysis. To measure total-factor energy efficiency, data envelopment analysis (DEA) has attracted great attention globally [6] since it can be easily adopted to a multiple input-output framework to compute the energy performance, which is more reasonable than using single-factor energy performance analysis. Many studies have measured energy efficiency or CO₂ emissions performance using DEA methods, mainly in regional or provincial level in China [7] . Some studies also adopted the directional distance function (DDF) to evaluate efficiency of China’s regions [8] [9] [10] . In this study, we use the global metal-frontier non-radial directional distance function, which covers all DMU and all periods, proposed by [11] to measure energy efficiency. This function has three strengths. First, it can isolate efficiency from overall technical efficiency. Moreover, efficiency analysis can incorporate in technological heterogeneity. Third, the discriminating power and comparability of the directional distance function model can be increased through constructing the global environmental technology frontier.

To evaluate dynamics of environmental productivity change, [12] was the first to propose a Malmquist-Luenberger (ML) index to compute environmentally sensitive productivity growth. Many empirical studies applying the ML index to measure green total-factor productivity growth, such as [13] [14] [15] [16] proposed a non-radial global Malmquist index which was developed by putting the non-radial distance function [17] and the global ML index [18] into a single framework. The integrated index can be used to measure dynamics free from the slack-neglecting problem as well as the infeasible solution challenge. In this study, we adopt the non-radial global Malmquist index [16] to evaluate the dynamic change of energy efficiency.

Meanwhile, we explain the evolution of regional inequalities in the provincial energy efficiency using Theil index, Gini index and CV index which are popular in the literature on regional inequality [19] [20] [21] [22] . However, most previous studies focus on the regional inequality of single-factor index, such as energy intensity [23] [24] [25] , and few analyze regional inequality based on a total-factor production process. In this paper, we analyze regional inequality based on a multiple input-output framework and decompose interprovincial inequality into between-region inequality and within-region inequality to determine regional characteristics.

The contributions of this study are twofold. First, the analysis target inequality in energy efficiency uses total-factor energy performance index, while previous inequality research has mainly focused on energy intensity or per capita energy. Second, previous studies mainly focus on total-factor performance of cross-sec- tional data, while we emphasize the evolution of energy efficiency and its dynamics over a 16-year period, which may yield richer insights regarding the development paths of energy efficiency and help policymakers to implement mitigation policies accordingly.

2. Methodology

2.1. Environmental Production Technology

Suppose that a decision making unit uses capital stock (K), labor force (L), and energy (E) as inputs to produce gross domestic product (Y) as a desirable output and CO₂ emissions (C) as an undesirable output. Therefore, we define an environmental production technology set, as follow:

(1)

According to the traditional production theory, we assume the environmental production technology is a closed and bounded set. This assumption means that finite inputs can only produce finite outputs [26] . Moreover, inputs and desirable outputs are assumed to be strongly disposable. Also, the environmental production technology is assumed to have weak disposability as well as null-jointness. The weak disposability assumption suggests that the decrease of undesirable output is costly in terms of a proportional decrease in desirable output. The null-jointness assumption means that a decision making unit should produce desirable and undesirable outputs simultaneously. We can express these two assumptions as follows:

1) If and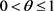, then.

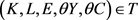2) If and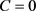, then.

Suppose that there are decision-making units and for decision-making unit i, the vector of three inputs, desirable outputs, and undesirable outputs can be expressed as. The environmental production technology for the decision making units exhibiting variable returns to scale (VRS) can be expressed as follows:

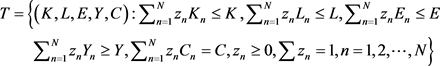(2)

where Z_n is an intensity variable. After constructing the environmental production technology, energy efficiency can be measured using the non-radial directional distance functions.

2.2. Global Non-Radial Directional Distance Function

We define the global environmental production technology as 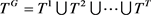following [18] . The global environmental production envelops indicates that it composes of all decision making units over the whole study period. In other words, all contemporaneous environmental production technologies are enveloped by global environmental production technology. In addition, we assume that all decision making units can access this global environmental production technology. The value of global NDDFs of a decision making unit can be denoted as, where the superscript G on 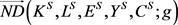means the global NDDF. 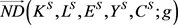can be evalluated by solving the following DEA-type model:

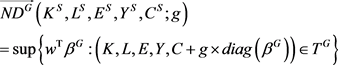
where means the normalized weight vector related to the number of inputs and outputs, 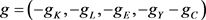is the explicit directional vector, the symbol diag means the diagonal matrices, and suggests the scaling factors indicating the individual inefficiency measure for K, L, E, Y and C. To evaluate the energy efficiency of each province, it is reasonable to consider all the factors' effect. In this study, we set the weight vector as (1/9, 1/9, 1/9, 1/3, 1/3), and the individual inefficiency of each factor can be evaluated as followings.

(3)

Based on these values for the GMNDDF, we have

(4)

TEPI^G measures the maximum possibility to reduce energy intensity, which can be used to measure energy efficiency of each province over a certain period of time. Obviously, TEPI^G lies between zero and unity, and the higher the TEPI^G, the better is energy efficiency. The province enjoys the best energy efficiency if TEPI^G equals to 1.

2.3. Dynamics

[16] combined the non-radial distance function and global Malmquist-Luenberger index to propose an integrated index, the non-radial global Malmquist index, which offers a way of evaluating the changes of efficiency free from the infeasibility and slack neglecting problem. Similarly, in this paper, we evaluate the dynamics of energy efficiency using the non-radial global Malmquist energy performance index (NGMEPI) as follows:

(5)

corresponds to efficiency gain; corresponds to efficiency loss.

The NGMEPI measures the changes in TEPI on T^G for the period between t and t + 1.

2.4. Inequality Measures

In this study, we focused on measures of dispersion, concentration, and entropy. Therefore, we evaluate the inequality of provincial energy efficiency through the coefficient of variation (CV), Gini coefficient and Theil Index.

CV is the simplest method to measure inequality, which is readily intelligible, but sensitive to outliers. The CV of energy efficiency indicates the standard deviation divided by the average energy efficiency and is calculated as follows:

(6)

where y_i is TEPI of province i, N is the number of provinces and y is the mean TEPI of all provinces. According to [21] , we adopted the unweighted CV which better shows disparities between regions, instead of the weighted CV, which better shows disparities between individuals.

The Gini coefficient is a widely used index based on the Lorenz Curve, but is unduly influenced by high values. The Gini Coefficient for energy efficiency is evaluated as follows:

(7)

where N is the number of provinces and is energy efficiency of the ith province, ordered by energy efficiency.

The Theil Index is a weighted entropy index, allowing an examination of the regional composition of inequality. The Theil Index is calculated as follows:

(8)

where y_i is the portion of TEPI of the ith province to the total energy efficiency of all sampled provinces and x_i is 1 to all sampled provinces.

This can be decomposed into between region and within region components as follows:

(9)

where T_br equals the total between region contribution to the Theil Index and T_wr equals the total contribution to the Theil Index from within regions. T_br is calculated as follows:

(10)

where is the portion of total TEPI of the r_th region to the total energy efficiency of all regions and is the portion of the amount of provinces of r_th region to the total amount of province of all regions, and N is the number of regions.

T_wr is calculated as follows:

(11)

where is a weighting of the portion of total energy efficiency to the total energy efficiency of all provinces, is the portion of TEPI of the i_th province in the r_th region to the total TEPI of the r_th region and is 1 to the amount of provinces within the r_th region.

3. Empirical Application

3.1. Data

In terms of the output variables, GDP was used to describe the desirable output of each province. The energy data were collected from the China Energy Statistical Yearbook from 2001-2017. Energy input was transformed into standard coal equivalents. The CO₂ emissions calculation method used in this study followed [27] . Employed persons at year-end in urban areas are used as the labor input, which is taken from the China Statistical Yearbooks and China Labor Statistical Yearbook. Because capital stock data are not available from official sources, we calculate the capital stock based on the perpetual inventory method:

(12)

In Equation (12), K_t, I_t, δ indicates the capital stock, investment in fixed assets, and depreciation rate at time t, respectively. K_t−1 refers to the capital stock in period t − 1. The monetary variables, including GDP and capital stock, are converted into 1978 constant price. Table 1 shows the descriptive statistics of 29 provinces in China from 2000 to 2015.

3.2. Region Division

There has a history about the regional division ways in geographic studies of China, whereas it is generally agreed that there are vast differences in determining how many regions China has, and what their borders are. The “three belts” scheme originating in the Seventh Five-Year Plan is not suitable to China’s actual conditions especially when the Western Development Program, the Northeast Area Revitalization Plan, the Rise of Central China Plan were proposed one after another after 2000. In this study, we adopt the four regional division, namely, eastern region, central region, western region and northeast region, put forward in the Eleventh Five-Year Plan (2006-2010).

In addition, we merge Chongqing with Sichuan because data for Chongqing independent of Sichuan for the period before 1997 are largely unavailable. Therefore, this study includes 29 provinces in total.

Figure 1 shows the regional division in China. In this study, we divide Chinese

29 provinces into 4 regions, namely, eastern region, central region, west region and northeast region. There are four colors in Figure 1 and these colors represent these four regions, respectively.

4. Empirical Results

4.1. Energy Efficiency and Dynamics

Table 2 documents each province’s TEPI and its rank in 2000, 2005, 2010 and 2016 as well as the NGMEPI during the three periods 2001-2005, 2006-2010 and 2011-2016. Regarding the national level, the average of total-factor energy performance is 0.49 in 2016, which indicates that 51% improvement could be made to reach the global technology frontier. At the region level, eastern region enjoyed the fastest total-factor energy performance growth from 2000 to 2016, namely −1% during 2000-2005, 7% during 2006-2010 and 6% during 2011-2016. It is worth noting that western region experienced a rapid growth rapid during 2011-2016 (2.8%) though it was a laggard previously. Considering specific province, TEPI of Tianjin, Shanghai, Jiangsu, Shandong and Guangdong was 1 in 2016, indicating that they had the best energy performance among all provinces. TEPI of Tianjin (1.00), Shanghai (1.00), Shandong (1.00), Guangdong (1.00), Jiangsu (1), Sichuan (0.90), Beijing (0.86), Hainan (0.71), Zhejiang (0.58), Fujian (0.58) and Hubei (0.52) in 2016 were above the national average (0.49). However, there were great potential for Xinjiang (0.11), Ningxia (0.15), Shanxi (0.16), Guizhou (0.20) and Inner Mongolia (0.24) to improve energy efficiency.

Table 3 shows the dynamics of 29 provinces over the study period. The national annual growth rates of the total-factor energy performance of Chinese provinces changed by approximately −3.0%, 2.1% and 3.4% under NGMEPI estimation during 2000-2005, 2006-2010, 2011-2016, respectively (NGMEPI minus one is equal to the growth rate of total-factor energy performance).These indicate that, on average, the ratio of target energy intensity to actual energy intensity decreased by 3.0% during 2000-2005, increased by 2.1% during 2006-2010 and 3.4% per year during 2011-2016. Shandong had the highest growth rate during 2011-2016 with 26.2% average growth rate followed by Guangdong (12.4%), Yunnan (11.5%), Jiangsu (10.9%), Jilin (9.1%). However, there are 8 provinces which fail to improve energy efficiency during 2011-2016 and their NGMEPI is smaller than 1, namely Qinghai (0.98), Heilongjiang (0.98), Ningxia (0.97), Xinjiang (0.97), Hainan (0.95), Fujian (0.92), Hunan (0.91) and Anhui (0.90).

4.2. Interprovincial Inequality

According to Figure 2, the CV, Theil Index, and Gini coefficient all revealed a similar trajectory of interprovincial inequality for the period from 2000 to 2016. The CV depicts a sharper decline of inequality over the study period than the other two indices. The net result is, interprovincial inequality in 2016 was about 13.8% lower, 16.3% higher, and 35.1% higher, than the 2000 level, according to

the CV, Gini coefficient, and the Theil index. Interprovincial inequality decreased slightly during 2000-2003, rose continuously during 2006-2016.

4.3. Interregional and Intraregional Inequalities

Figure 3 shows the details of the inequalities by decomposing the Theil index into between-region and within-region inequality. Figure 3 shows that the contributions of these components’ inequality varied over time. The intraregional components of the Theil Index can be further decomposed into contributions by region, namely eastern region, Central region, west region and northeast region.

In general, within-region inequality was higher than between-region inequality from 2000 to 2015. Within-region inequality determined the overall trend of interprovincial inequality, so both of them have similar varying tendency. Intraregional inequality decreased from 0.1063 in 2000 to 0.0672 in 2003, rose steadily

to 0.1048 in 2010, with the exception of the year 2008 when it declined suddenly to 0.09. Moreover, intraregional inequality declined continuously between 2010 and 2016 and dropped to 0.0743 in 2016. Interregional inequality remained relatively low from 2000 to 2002, increase steadily following years, rising to 0.0838 in 2016. Noticeably, in 2016, within-region inequality was overtaken by between- region inequality for the first time.

Between 2000 and 2003, interprovincial inequality decreased rapidly and the decrease of intraregional inequality can account for this trend. However, the decline of interprovincial and intraregional inequality between 2000 and 2003 did not constitute long-term regional convergence but rather was a short-lived phenomenon.

From 2003 to 2012, interprovincal and intraregional inequality increased steadily which can be interpreted as evidence for the Rise of Central China Plan proposed in 2004. The plan might led to the significant increase of energy efficiency in Anhui, from 0.679 in 2004 to 1 in 2012, and decrease of energy efficiency in Shanxi (from 0.209 in 2004 to 0.129 in 2012). Intraregional inequality from Western region decreased significantly and it might be interpreted as evidence for the Western Development Program carried out in 2009. Energy efficiency of Ningxia (from 1 in 2000 to 0.243 in 2008), Sichuan (from 1 to 0.773 in 2008), Shaanxi (from 0.322 in 2000 to 0.252 in 2008) and Inner Mongolia (from 0.302 in 2000 to 0.151 in 2008) decreased during 2000-2008. After 2008, intraregional inequality form Western region experienced an increasing trend. In 2008, Theil index of interprovincial inequality reduced to 0.1151 suddenly, which might be interpreted as the negative effect of the economic crisis that started in 2008. The decline of interregional inequality in 2008 was the result of the decrease of intraregional inequality in eastern as well as western region.

From 2012-2016, the trend of the inequality of inequality components changed significantly. Interprovincial inequality experienced a sudden decrease in 2012, which might be interpreted by the launch of a 4 trillion-yuan stimulus plan. This plan was proposed to stimulate the economy and construct infrastructure, which boosted high energy consuming industries in short time and also promote energy saving and emission reduction in the long run. From 2013 to 2016, interprovincial inequality saw a gradual increase, rising from 0.1318 to 0.1581. In terms of within-region inequality, it decreased from 0.1017 in 2012 to 0.0743 in 2016. However, between-region inequality experienced an increasing trend, rising from 0.0436 in 2012 to 0.0838 in 2016.

Figure 4 illustrates that throughout the period studied, the between-region component of the TEPI Theil Index contributes 0.0107 in 2000 and 0.0838 in 2016, while the within-region components of the TEPI Theil Index is 0.1063 in 2000 and 0.0743 in 2016. Within-region inequality of eastern region fluctuated over the study period, at 0.0279 in 2000 and 0.0266 in 2016. As for within-region of central region, it increases from 0.0191 in 2000 to 0.0298 in 2010, and decreases to 0.0082 in 2016. In terms of within-region inequality of western region, it decreases from 0.0593 in 2000 to 0.0210 in 2008, and then increases to 0.0423

in 2016. As for northeast region, the amount of it is negligible over the study period.

Table 4 shows the share of inequality of various components between 2000 and 2016. Within-region inequality is the main contributor of the total inequality during 2000-2015. In other words, in 2000, with-in region inequality accounts for 90.85% of the total inequality, while it decreases to 46.99% in 2016. As for within

region inequality of these four regions, within-region inequality of eastern region contributes 23.87% of the total inequalities in 2000 and decreases to 16.84% in 2016. However, the proportion of within-region inequality from Western region decreases from 50.66% in 2000 to 26.76% in 2016 but have a sudden decrease in 2016 (11.03%). Central and northeast components account for a relatively small proportion of total inequality, representing 5.18% and 0.23% in 2016, respectively. In general, within-region inequalities of eastern and central regions are the main contributor to total inequality compared with that of western and northeast regions.

5. Conclusions

In this study, we measure energy efficiency of 29 provinces in China from 2000 to 2016 using total-factor energy performance index (TEPI) based on the global metal-frontier non-radial directional distance function. We further investigate the dynamics of energy efficiency to evaluate the provincial efforts made to improve energy efficiency by non-radial global Malmquist energy performance index (NGMEPI). Lastly, the between-region and within-region inequalities of energy efficiency are investigated using Theil index.

The empirical results are summarized below. First, the national TEPI is 0.49 in 2016, which indicates that 51% improvement could be made to reach the global technology frontier. At the region level, eastern region enjoyed the fastest energy efficiency improvement from 2000 to 2016, with −1% annual growth rate from 2001 to 2005, 7% from 2006 to 2010 and 6% from 2011 to 2016. It is worth noting that northeast region enjoyed a high growth rate during 2011-2016 though it was a lagger previously. Considering specific provinces, TEPI of Tianjin, Shanghai, Jiangsu, Guangdong and Shandong was 1 in 2016, indicating that they had the best energy efficiency. However, Xinjiang and Ningxia had the lowest energy efficiency. This may be interpreted that Ningxia has the sixth largest proven coal reserves in China, and the pillar industry is secondary industry, such as metallurgical industry and building materials industry, which consumes a large amount of energy. Therefore, energy efficiency of Ningxia was relatively low. Similarly, Xinjiang is the fourth largest coal production in China and depend heavily on energy; therefore its energy efficiency was the lowest in 2016.

Second, the national annual growth rates of TEPI of China’s provinces changed by approximately −2.3%, 2.1% and 3.4% during 2001-2005, 2006-2010 and 2011-2016, respectively. Among 29 provinces, Shandong had the highest growth rate during 2011-2016 with 26.2% average growth rate followed by Guangdong (12.4%) and Yunnan (11.5%). In comparison, the annual growth rates of TEPI of Qinghai, Heilongjiang, Ningxia, Xinjiang, Hainan, Fujian, Hunan and Anhui were negative, indicating the energy efficiency of these provinces decreased during 2011-2016.

Lastly, compared with between-region inequality, within-region inequality was the main contributor to interprovincial inequality. Within-region inequality from eastern and western region is larger than that from central and northeast region over the study period.

Based on these empirical results, we now suggest some policy implications. First, policymaker should lay more emphasis on Xinjinag, Ningxia, Shanxi and Guizhou to improve energy efficiency. These provinces can learn some experience from Tianjin, Shanghai, Shandong, Guangdong and Jiangsu which had the best energy efficiency in 2016. Second, Qinghai, Heilongjiang, Ningxia, Xinjiang, Hainan, Fujian, Hunan and Anhui require more effective measures to improve energy efficiency, such as green technology investment and improving the quality of energy mix, because their energy efficiency decreased between 2011 and 2016.

Acknowledgements

This work was supported by Natural Science Foundation of Guangdong (No. 2016A030313091) and it is a part of the research findings of “Study of innovative city evaluation index system based on implement of innovation-driven development strategy: A case study from Guangdong province”. Thank my brother, roommates and tutor for their suggestions and thank Taylor Swift.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Xiao, H.J. and Mei, L.H. (2019) Dynamics and Inequalities in Energy Efficiency in China. Energy and Power Engineering, 11, 132-148. https://doi.org/10.4236/epe.2019.113008

References