Energy and Power Engineering
Vol.09 No.08(2017), Article ID:78187,11 pages
10.4236/epe.2017.98028
Modelling Study of Magnetic Field Effect on the Performance of a Silicon Photovoltaic Module
Dioari Ulrich Combari1, Issa Zerbo1, Martial Zoungrana1, Emmanuel Wendsongre Ramde2, Dieudonné Joseph Bathiebo1
1Laboratory of Thermal and Renewable Energies, Department of Physics, University Ouaga I Prof. Joseph KI-ZERBO, Ouagadougou, Burkina Faso
2Department of Mechanical Engineering, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 8, 2017; Accepted: August 4, 2017; Published: August 7, 2017
ABSTRACT
Solar Photovoltaic is a very promising solution that can greatly contribute in solving the increasing global energy demand. In both rural and urban areas, photovoltaic modules are in some instances installed close to telecommunication antennas or voltage transformers which generate important magnetic fields in their vicinity. The question is whether or not these magnetic fields affect the performances of the photovoltaic installations. This article presents a modelling study of external magnetic field effect on the electrical parameters of a photovoltaic module. The photocurrent, the photovoltage, the electric power, the series and the shunt resistances of the photovoltaic module, made up of ideal cells, are deduced from those of a silicon solar cell. Then, the I-V and P-V curves are plotted and the theoretical values of the electrical parameters of the photovoltaic module are deduced. The series and shunt resistances of the photovoltaic module are calculated using well known equations and the previous electrical parameters. The results show the negative effect of magnetic field on the performance of a solar photovoltaic module.
Keywords:
Conversion Efficiency, Magnetic Field, Modelling Study, Photovoltaic Module, Series Resistance, Shunt Resistance

1. Introduction
Solar Photovoltaic is a very promising solution that can contribute in solving the increasing energy demand. The performance of photovoltaic systems depends on a number of parameters such as ambient temperature, solar irradiance, sunshine duration, relative humidity, atmospheric concentrations of aerosols (harmattan dust particles for example), windspeed, wind chill and direction, rainfall, mode of installation and orientation (rooftop or ground-mounted) etc. [1] [2] .
The challenge of researchers is twofold: the first challenge is to improve solar cells efficiency through their manufacturing technique and the second challenge is to examine the characteristics of PV modules and the external factors (environmental conditions) that affect them.
In order to investigate the effect of external factors on PV modules, various researchers have used theoretical methods under different environmental conditions and arrived at different results.
Nema et al. [3] and Asghar et al. [4] both proposed Matlab/simulink models of PV cells and simulated the effects of temperature and solar irradiation on the electrical performances of PV modules. The PV cells were modelled with the single exponential equation and Simulink was used to simulate the performance of the PV cells/modules under varying solar irradiation and temperature. The authors concluded that the open circuit voltage decreases linearly with an increase in the cell temperature but increases logarithmically with an increase in solar radiation. The short-circuit current on the other hand was said to be a linear function of the solar irradiation. It increases with an increase in solar irradiation as well as an increase in temperature. In a similar vein, Skoplaki et al. [5] studied the effects of temperature on both the electrical efficiency and power output of PV modules. They concluded that the electrical efficiency and the power output of a PV module decrease linearly with an increasing operating temperature. Alsayid et al. [6] and Boukebbous et al. [7] , with a Matlab/simulink model, also simulated the impact of partial shading on the performance of PV modules. The simulation results showed that, under partially shaded conditions, the maximum power produced by PV modules decreases. Besides these studies, Siddiqui et al. [8] used one year data to develop empirical correlations between the efficiency of solar photovoltaic modules and ambient temperature as well as wind speed. The correlated equations can predict with good accuracy the efficiency of a PV module with respect to ambient temperature and wind speed for a particular location. Besides these climatic and seasonal parameters, other researchers proposed studying the modelling of the effect of magnetic field on the properties of solar cells. Madougou et al. [9] showed that, for each illumination mode of the bifacial solar cell, the photocurrent density decreases with the magnetic field while the photovoltage increases with the magnetic field for front side and simultaneous front and back side illumination. At last, the authors concluded that the I-V characteristics of the bifacial silicon solar cell decrease with the magnetic field. Zerbo et al. [10] [11] showed that the maximum electric power and the conversion efficiency of a bifacial solar cell decrease with the increase of magnetic field while the fill factor and the load resistance at the maximum power point increase. In a similar vein, Zoungrana et al. [12] studied a silicon solar cell under an intense light concentration and obtain the same results as Zerbo et al. [10] [11] .
The aim of this work is to investigate the deterioration effect of magnetic field on the performance of a photovoltaic module. This is done by simulation, on a PV module made up of ideal solar cells, by finding the electrical parameters such as the current and voltage at maximum power point, the short-circuit-current, the open circuit voltage, the maximum electric power, the fill factor, the conversion efficiency and the charge resistance at the maximum power point using simultaneously the I-V and P-V characteristics. Then, the series and shunt resistances of the photovoltaic module are calculated using equations developed by some researchers and the electrical parameters mentioned previously.
2. Theoretical Background
The PV module is made up of one branch of 36 mono-facial cells connected in series. The synoptic scheme of the photovoltaic module is given in Figure 1.
To investigate the effect of the external magnetic field on the electrical parameters of the PV module, we applied a variable external magnetic field, parallel to the surface of the n-p junction of the 36 mono-facial cells, as shown for a silicon solar cell in previous works [10] [11] .
2.1. Effect of Magnetic Field on I-V Characteristics
For a monocrystalline photovoltaic module, which is made up of Np parallel branches with each branch involving Ns cells in series, the photocurrent can be expressed by Equation (1).
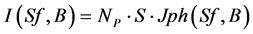 (1)
(1)
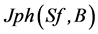 is the photocurrent density of a silicon solar cell under magnetic field [9] [10] [11] [12] .
is the photocurrent density of a silicon solar cell under magnetic field [9] [10] [11] [12] .
In the same way, the voltage of the photovoltaic module depends on the number of cells Ns connected in series. This is expressed by Equation (2).
 (2)
(2)
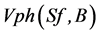 is the photovoltage of a silicon solar cell under magnetic field [9] [10] [11] [12] .
is the photovoltage of a silicon solar cell under magnetic field [9] [10] [11] [12] .
It appears in the expressions of I and V that they depend on junction dynamic velocity, Sf [10] . The variations of this parameter (junction dynamic velocity) lead to the values of I and V.
Figure 2 presents the I-V characteristic curves of the photovoltaic module for different values of the magnetic field’s intensity.
Figure 1. Synoptic scheme of photovoltaic module.
Figure 2. Photocurrent-photovoltage characteristic versus intensity of magnetic field (L = 0.02 cm; H = 0.03 cm; D = 35 cm2/s; μn = 1350 cm2/V∙s, Np = 1, NS = 36, S = 7.5 cm2).
I-V curves of the photovoltaic module have the same shape than those of a silicon solar cell [11] . It can be noted that, for an increasing intensity of the magnetic field, the short-circuit current decreases considerably while the open circuit voltage increases slightly. Furthermore, it can be observed that as the intensity of the magnetic field increases, the maximum power point is shifted towards higher values of the photovoltage and lower values of the photocurrent. This situation corresponds to a displacement of the operating point of the photovoltaic module and subsequently an increase of the charge resistance at the maximum power point [11] .
2.2. Effect of Magnetic Field on P-V Characteristics
The electric power delivered by the monocrystalline solar photovoltaic module to an external circuit is expressed by Equation (3):
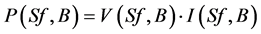 (3)
(3)
The electric power delivered by the solar photovoltaic module to an external circuit depends also on the junction dynamic velocity Sf. While taking the junction dynamic velocity as a variable, Figure 3 is a plot of the photovoltaic module P-V characteristic curves for different values of the intensity of the magnetic field.
The P-V characteristic curves of the photovoltaic module have also the same shape than those of a silicon solar cell [11] . From the various curves in Figure 3, it can be observed that firstly, at any specified intensity of the magnetic field, the electric power increases with the photovoltage, reaches a peak and then decreases with increasing photovoltage; secondly, at any given photovoltage, the electric power decreases as the intensity of the magnetic field increases; thirdly, as the intensity of the magnetic field increases, the curves shifts to the right,
Figure 3. Electric power-photovoltage characteristic versus intensity of magnetic field (L = 0.02 cm; H = 0.03 cm; D = 35 cm2/s; μn = 1350 cm2/V∙s, Np = 1, NS = 36, S = 7.5 cm2).
compelling the peak electric power to occur at higher photovoltage. This results in an increase of the charge resistance at the maximum power point and that corresponds to a displacement of the photovoltaic module’s operating point [11] .
2.3. Effect of Magnetic Field on the Series Resistance
The series resistance is caused by the movement of electrons through the emitter and the base of a solar cell, the contact resistance between the metal contact and the silicon and the resistance of metal grids at the front and the rear of the solar cell [13] .
We extrapolate the equation of the series resistance of a silicon solar cell [13] [14] [15] to a PV module. Consequently, the expression of the series resistance of a PV module is given by Equation (4a):
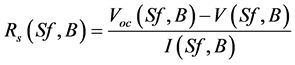 (4a)
(4a)
Taking into account Equation (1) and Equation (2), Equation (4a) becomes:
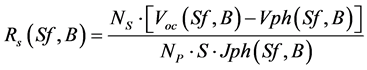 (4b)
(4b)
We consider a PV module made up of n sets of Np parallel branches connected in series. Each branch consists of Ns cells connected in series. The Equation (4b) becomes:
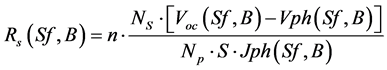 (4c)
(4c)
The series resistance of a PV module can be written according to the series resistance of each solar cell of the PV module.
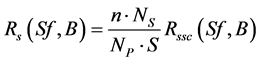 (4d)
(4d)
with 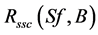 which is the series resistance of a solar cell.
which is the series resistance of a solar cell.
The curve of the series resistance versus magnetic field intensity is plotted in Figure 4.
The curve in Figure 4 shows that the series resistance increases with the magnetic field. The increase of the series resistance leads to a decrease of the current provided by PV module to an external load.
2.4. Effect of Magnetic Field on the Shunt Resistance
The shunt resistance is due to manufacturing defects and also lightly by poor solarcell design. It corresponds to an alternate current path for the photocurrent [13] . In the Shockley five-parameter model of a solar cell, a shunt resistance represents the leakage current along the edges of the solar cell [16] . The shunt resistance is indicative of good or bad quality of a solar cell because when it is large, the leakage current through the solar cell is low and vice versa [15] .
We extrapolate also the equation of the shunt resistance of a silicon solar cell [13] [14] [15] to a PV module. Thus, the expression of the shunt resistance of a PV module is given by Equation (5a):
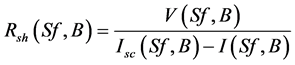 (5a)
(5a)
For a PV module made up of n sets of Np parallel branches connected in series, in which each branch consists of Ns cells connected in series, the Equation (5a) becomes:
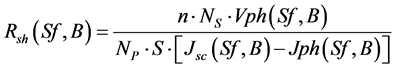 (5b)
(5b)
Figure 4. Series resistance versus magnetic field intensity (D = 35 cm2∙s−1; μ = 1350 cm2∙(V∙s)−1; L = 0.02 cm; H = 0.03 cm; n = 1; Np = 1; Ns = 36; S = 7.5 cm2; Sf = 1 cm∙s−1).
Thus, the shunt resistance of PV module can be written according to the shunt resistance of a solar cell:
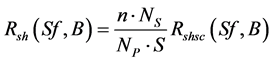 (5c)
(5c)
with 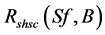 which is the shunt resistance of a solar cell.
which is the shunt resistance of a solar cell.
We plot in Figure 5 the curve of the shunt resistance versus magnetic field intensity.
The curve in Figure 5 shows that the shunt resistance increase with the magnetic field. The increase of the shunt resistance of the photovoltaic module means a decrease of the losses of carriers at the junction of its solar cells.
3. Results and Discussion
3.1. Method of Electrical Parameters Determination
3.1.1. Determination of Electrical Parameters Using I-V/P-V Method
We present in this section a method to determine the electrical parameters of the photovoltaic module (current and voltage at maximum power point, maximum electric power, fill factor, conversion efficiency and charge resistance at the maximum power point).
For that, we plot in the same axes system the I-V and P-V curves for a given magnetic field intensity. Using simultaneously the I-V and P-V curves, we determine the values of the maximum electric power Pm, the voltage and current at the maximum power point
The fill factor (FF) of the photovoltaic module is then calculated using Equation (6):

Figure 5. Shunt resistance versus magnetic field intensity (D = 35 cm2∙s−1; μ = 1350 cm2∙(V∙s)−1; L = 0.02 cm; H = 0.03 cm; n = 1; Np = 1; Ns = 36; S = 7.5 cm2; Sf = 108 cm∙s−1).
The determination of the voltage and the current at the maximum power point 

The conversion efficiency of the photovoltaic module is calculated using Equation (8):

Pinc is the power of the incident light’s flux and Pinc = 1000 W/m2 in Air Mass 1, 5 standard conditions. Smod is the area of the photovoltaic module that receives the incident light.
3.1.2. Determination of Series and Shunt Resistances
The theoretical values of the series and shunt resistances of the PV module are calculated, according to the magnetic field, using Equation (9) and Equation (10) [18] and the values of Table 1.


3.2. Values of Electrical Parameters of the PV Module
3.2.1. Electrical Parameters Using I-V/P-V Method
The PV module is made up of 36 cells connected in series. Each cell has an area of 7.5 cm2. Therefore, the PV module area is: 
The characteristic values of the PV module under magnetic field are given in Table 1.
Table 1. Electrical parameters of the PV module under magnetic field.
These results show that the current at maximum power point and the short- circuit current decrease considerably while the voltage at maximum power point and the open circuit voltage increases weakly with the increase of the magnetic field intensity. Thus, the intensities of current decrease strongly for a slightly increase of the different voltage when the magnetic field intensity increases. That explains the decrease of the maximum electric power and the conversion efficiency.
Conversely, we have observed an increase of the fill factor and the charge resistance at the maximum power point. But, for a given charge resistance, the increase of magnetic field induced a decrease of the maximum electric power and the conversion efficiency, and therefore the magnetic field causes a deterioration of the performance of the PV module.
These results are in agreement with the theoretical ones of a silicon solar cell [11] .
3.2.2. Values of Series and Shunt Resistance
The values of the series and shunt resistances of the PV module under magnetic field are given in Table 2.
These results confirm that the values of the series and shunt resistances of the PV module increase when the magnetic field intensity increases. The increase of the value of the shunt resistance of the photovoltaic module means a decrease of the losses of carriers at the junction of its solar cells while the increase of the value of the series resistance means a decrease of the current provided by the photovoltaic module to the external load.
The increase of the series and shunt resistances and the decrease of the current provided by the photovoltaic module to the external load show that the photovoltaic module has a resistive behavior under magnetic field as a solar cell [10] . This resistive behavior under the magnetic field is the magnetoresistance.
4. Conclusions
A theoretical study of magnetic field effects on the electrical parameters of silicon photovoltaic module is presented.
The maximum electric power, the voltage at the maximum power point, the current at the maximum power point, the short-circuit current and the open circuit voltage are determined by means of the theoretical I-V and P-V characteristics. Then we calculated the fill factor (FF) of the photovoltaic module, the conversion efficiency and the charge resistance at the maximum power point using Ohm’s law.
Table 2. Series and shunt resistance of the PV module under magnetic field.
The numerical data are evidence of a decrease in the maximum electric power and the conversion efficiency with the increase of magnetic field intensity while the fill factor and the resistance at the maximum power point increase. The increase of the values of the series and shunt resistance of the photovoltaic module under magnetic field puts resistive behavior called magnetoresistance in evidence.
As in the case of a silicon solar cell, the magnetic field causes a deterioration of the performance of a photovoltaic module.
Acknowledgements
The authors are grateful to International Science Program (ISP) for supporting their research group (energy and environment) and allowing them to conduct this work.
Cite this paper
Combari, D.U., Zerbo, I., Zoungrana, M., Ramde, E.W. and Bathiebo, D.J. (2017) Modelling Study of Magnetic Field Effect on the Performance of a Silicon Photovoltaic Module. Energy and Power Engineering, 9, 419-429. https://doi.org/10.4236/epe.2017.98028
References
- 1. Koffi, H.A., Kakane, V.C.K., Kuditcher, A., Hugues, A.F., Adeleye, M.B. and Amuzu, J.K.A. (2015) Seasonal Variations in the Operating Temperature of Silicon Solar Panels in Southern Ghana. African Journal of Science, Technology, Innovation and Development, 7, 485-490.
https://doi.org/10.1080/20421338.2015.1038006 - 2. Dia, F., Mbengue, N., Diagne, M., Niasse, O. A., Ba, B. and Séne, C. (2016) Contribution to the Study of the Degradation of Modules PV in the Tropical Latitudes: Case of Senegal. Research Journal of Applied Sciences, Engineering and Technology, 12, 427-438.
https://doi.org/10.19026/rjaset.12.2383 - 3. Nema, S., Nema, R.K. and Agnihotri, G. (2010) Matlab/Simulink Based Study of Photo-voltaiccells/Module/Array and Their Experimental Verification. International Journal of Energy and Environment, 1, 487-500.
- 4. Asghar, S. B.and Singh, R. K. (2015) Simulink Based Analysis and Realization of Solar PV System. Energy and Power Engineering, 7, 546-555.
https://doi.org/10.4236/epe.2015.711051 - 5. Skoplaki, E. and Palyvos, J.A. (2009) On the Temperature Dependence of Photovoltaic Module Electrical Performance: A Review of Efficiency/Power Correlations. Solar Energy, 83, 614-624.
https://doi.org/10.1016/j.solener.2008.10.008 - 6. Alsayid, B.A., Alsadi, S.Y., Jallad, J.S. and Dradi, M.H. (2013) Partial Shading of PV System Simulation with Experimental Results. Smart Grid and Renewable Energy, 4, 429-435.
https://doi.org/10.4236/sgre.2013.46049 - 7. Boukebbous, S.E. and Kerdoun, D. (2015) Study, Modeling and Simulation of Pho-tovoltaic Panels under Uniform and Non-Uniform Illumination Conditions. Revue des Energies Renouvelables, 18, 257-268.
- 8. Siddiqui, R. and Bajpa, U. (2012) Deviation in the Performance of Solar Module under Climatic Parameter as Ambient Temperature and Wind Velocity in Composite Climate. International Journal of Renewable Energy Research, 2, 486-490.
- 9. Madougou, S., Made, F., Boukary, M. S. and Sissoko, G. (2007) I-V Characteristics for Bifacial Silicon Solar Cell Studied under a Magnetic Field. Advanced Materials Research, 18-19, 303-312.
https://doi.org/10.4028/www.scientific.net/AMR - 10. Zerbo, I., Zoungrana, M., Sourabie, I., Ouedraogo A., Zouma B. and Bathiebo, D.J. (2015) External Magnetic Field Effect on Bifacial Silicon Solar Cell’s Electric Power and Conversion Efficiency. Turkish Journal of Physics, 39, 288-294.
https://doi.org/10.3906/fiz-1505-10 - 11. Zerbo, I., Zoungrana, M., Sourabie, I., Ouedraogo, A., Zouma, B. and Bathiebo, D.J. (2016) External Magnetic Field Effect on Bifacial Silicon Solar Cell’s Electrical Parameters. Energy and Power Engineering, 8, 146-151.
http://dx.doi.org/10.4236/epe.2016.83013 - 12. Zoungrana, M., Zerbo, I., Soro, B., Savadogo, M., Tiedrebeogo, S. and Bathiebo, D.J. (2017) The Effect of Magnetic Field Effect on the Efficiency of a Silicon Solar Cell under an Intense Light Concentration. Advances in Science and Technology Research Journal, 11, 133-138.
https://doi.org/10.12913/22998624/69699 - 13. Mbodji, S., Ly, I., Diallo, H.L., Dione, M.M., Diasse, O. and Sissoko, G. (2012) Modeling Study of N+/P Solar Cell Resistances from Single I-V Characteristic Curve Considering the Junction Recombination Velocity (Sf). Research Journal of Applied Sciences, Engineering and Technology, 4, 1-7.
- 14. Toure, F., Zoungrana, M., Zouma, B., Mbodji, S., Gueye, S., Diao, A. and Sissoko, G. (2012) Influence of Magnetic Field on Electrical Model and Electrical Parameters of a Solar Cell under Intense Multispectral Illumination. International Journal of Advances in Science and Technology, 5, 40-53.
- 15. Sané, M. and Barro, F.I. (2015) Effect of Both Magnetic Field and Doping Density on Series and Shunt Resistances under Frequency Modulation. Indian Journal of Pure and Applied Physics, 53, 590-595.
- 16. Koffi, H.A., Kuditcher, A., Kakane, V.C.K., Armah, E.A., Yankson, A.A. and Amuzu, J.K.A. (2015) The Shockley Five-Parameter Model of a Silicon Solar Cell: A Short Note. African Journal of Science, Technology, Innovation and Development, 7, 491-494.
http://dx.doi.org/10.1080/20421338.2015.1038007 - 17. Sow, O., Zerbo, I., Mbodji, S., Ngom, M.I., Diouf, M.S. and Sissoko, G. (2012) Silicon Solar Cell Under Electromagnetic Waves in Steady State: Electrical Parameters Determination Using the I-V and P-V Characteristics. International Journal of Science Environment and Technology, 1, 230-246.
- 18. Abdul Kareem, M.S. and Saravanan, M. (2016) A New Method for Accurate Estimation of PV Module Parameters and Extraction of Maximum Power Point under Varying Environmental Conditions. Turkish Journal of Electrical Engineering and Computer Sciences, 24, 2028-2041.
https://doi.org/10.3906/elk-1312-268








