Energy and Power Engineering
Vol.09 No.03(2017), Article ID:75092,17 pages
10.4236/epe.2017.93013
The Relationship between Energy Consumption and Economic Growth in the USA: A Non-Linear ARDL Bounds Test Approach
Arzu Tay Bayramoglu*, Ertugrul Yildirim
Department of Economics, Zonguldak, Turkey
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 24, 2016; Accepted: March 28, 2017; Published: March 31, 2017
ABSTRACT
We study the relationship between energy consumption and economic growth in the case of USA by using an asymmetric ARDL bounds test approach to achieve the actual model. The quarterly data set covers the period of 1973:1- 2013:4. The findings indicate that the effect of energy consumption is asymmetric in the long term but not in the short term. In the long run, the effect of negative component of energy consumption on economic growth is small and statistically insignificant. The coefficient of the positive component of energy consumption is found about 0.9 and statistically significant at 1% level. We conclude that energy saving policies such as technological progress and organizational rearrangements may have the dimmer effect for the impact of a negative component of energy consumption and the booster effect for impact of the positive component of energy consumption. Thus, energy saving policy should be tightly followed by the goal of high economic growth.
Keywords:
Energy Consumption, Economic Growth, Non-Linear ARDL Bounds Test, USA

1. Introduction
According to the neoclassical theory, energy inputs are accepted as auxiliary inputs in production. It is possible to assume that not only, there is a certain effect of energy inputs on a production level, but also the unidirectional causal nexus runs from economic growth to energy consumption [1] [2] [3] . By this way, economic growth is not automatically affected by any constraint in energy supply and such a case, the policies conducted with the purpose of reducing energy consumption can be pursued together with the economic growth policies. Moreover, this approach supposes that it is not necessary to decrease living standards in global terms while struggling with environmental problems such as climate change or possible insufficiency in fossil fuels.
On the contrary to neoclassical model, the ecological economics intellectual tradition highlights that scarce resource may create a restraining impact on the growth especially in industrialized economies [4] . As such, from this point of view, in the case of any scarcity in energy supply, it is possible to assume that the global living standards may be exposed to the negative impact of this scarcity on the contrary of what the neoclassical approach supposes [5] .
The schools of ecological economists claim that there is a certain impact on the economic development created by energy, and energy significantly and directly affected industrial revolution as well. Besides, this school of thought supposes that although substation of capital and energy by technological improvements may support overcoming the scarce resources, the role of this substation can only produce a minor positive impact [6] . The representatives of the school such as [7] [8] [9] also suggest that the impact of technological improvements has been exaggerated. They suppose that there are two different scenarios; according to the first one, productivity increases mainly due to innovations, which are arising from increased consumption of energy, and the according to the second one, innovations for increasing productivity can only be made by allowing the use of more energy. As such, it is assumed that along with the other minor causes, the most important trigger of the economic growth is increasing use of energy.
Despite the certain distinction on the impact of energy consumption in economic growth between the approaches of neoclassical and ecological schools, it is possible to state that neoclassical economics and ecological economics admit that there is a certain long-standing relation between economic development and use of energy. Against this consensus, the disagreement between these two approaches is to the short and long term direction of these mutual influences. There are major studies, which question the presence and direction of the causative nexus between energy consumption and economic growth through Granger causality techniques [5] .
The causality methodology analyses two main hypotheses as for the energy-led growth hypothesis and the growth-led energy hypothesis. In this context, Granger-causality produces four different alternatives on the possible consequences of causality. The first of is the growth hypothesis assuming that there is one-way causal nexus running from energy consumption to economic growth. The second is the conservation hypothesis suggesting that there is a one-way causal relation from economic growth to energy consumption. According to the feedback hypothesis, bi-directional causality from energy consumption to economic growth, when the last one, the neutrality hypothesis, assumes that there is no causal nexus between energy consumption and economic growth [10] .
By the growth hypothesis, conducting energy saving policies with the purpose of protecting the environment may create an adverse impact on the present state of economic growth if energy consumption Granger causes economic growth. When the growth, conservation and feedback hypotheses highlight some linear causal relations between energy consumption and economic growth, they neglect the effect of technological progress on the energy-growth nexus. In the highly industrialized economies, technological advances mainly originate, this relationship can change. That is to say technological advancement improves energy efficiency, leading to lower energy prices and more energy consumption using “rebound” or “take-back” effect, as first postulated by [11] [12] and much more economic growth. Furthermore, if using new energy-efficient technologies affect energy conservation and substitution level of fossil fuels by alternative energy inputs, the trade-off between energy and growth may become less severe. Thus, when energy consumption falls due to the increase in energy efficiency, economic growth cannot be affected negatively.
According to [13] , as pointed out by Solow, effect of energy consumption on economic growth is based on the size of elasticity of factor substitution. If the elasticity of factor substitution between energy other inputs is less than 1.0, improvements to technical efficiency will cause a decrease in energy consumption. If the elasticity of factor substitution between energy and other inputs is greater than 1.0, energy consumption will increase. The elasticity of substation between energy and other inputs in the case of USA has been analyzed in the literature, and most of the studies found that the elasticity is less than 1 [14] . Furthermore, as seen in [15] , if expenditures on energy services do not involve a significant share of total economic activity and energy costs do not substantially affect the total cost of energy services, progress in efficiency improvements will yield long-run reductions in energy use under the assumptions of the neoclassical growth model.
As a result, decreased energy consumption due to technological advancement may not necessarily lead to economic contraction, while increased energy consumption concurrent with energy efficient technological progress may cause an extraordinary level of economic growth. These are the mechanisms which this study refers to as dimmer and booster effects of energy efficiency improving technological advances. As a result of these mechanisms, there may be an asymmetric causal relation between energy consumption and economic growth.
The purpose of this study is to contribute to the empirical literature and generate policy suggestion concerning the energy consumption and economic growth nexus. The contributions of our study are threefold. First, following the modeling strategy developed [16] neglected asymmetric relationship dimension is added to the empirical literature analyzing the co-integrating relationship between energy consumption and economic growth. Second, both in the short and long run, the asymmetric adjustment patterns of positive and negative shocks in energy consumption to the economic growth are observed via impulse-response functions. Lastly, the policy suggestions, presented in light of the findings of this empirical experiment are more compatible with real life implementations.
The rest of the paper is organized as follows: The next section summarizes the empirical literature, testing the energy consumption-economic growth nexus. The used data and modeling strategy, followed in this study, is described in Section 3. Empirical findings are presented in Section 4. The last section consists of conclusion and policy implications of the paper.
2. Literature
Since the form of energy consumption-economic growth relationship may affect a wide range of policies such as energy, trade, innovation incentive, environmental, resource allocation, urbanization, employment and finance policies, extant research tries to find a proper modeling strategy to obtain robust findings of energy consumption and economic growth relationship. However, the findings in empirical studies are highly conflicting. Most of these studies follow various types of linear models. Few studies adapt non-linear modeling strategies to the relationship between energy consumption and economic growth. Since energy consumption and economic growth series are order one, 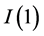 , nonlinear modeling in the context of co-integrating long-run relationships is important. Nonlinearity is formulated into the error correction mechanism and the procedure advances on three alternative error correction model approaches which are the threshold error correction model, the Markov-Switching error correction model and the smooth transition error correction model. However, they neglect the asymmetric relationships, since the three error correction model approach has the common assumption of the underlying co-integrating relationship may be represented as a linear combination of the underlying non-stationary variables. In general, an asymmetry or non-linearity may be a more accurate definition for the co-integrating relationship.
, nonlinear modeling in the context of co-integrating long-run relationships is important. Nonlinearity is formulated into the error correction mechanism and the procedure advances on three alternative error correction model approaches which are the threshold error correction model, the Markov-Switching error correction model and the smooth transition error correction model. However, they neglect the asymmetric relationships, since the three error correction model approach has the common assumption of the underlying co-integrating relationship may be represented as a linear combination of the underlying non-stationary variables. In general, an asymmetry or non-linearity may be a more accurate definition for the co-integrating relationship.
As discussed by [17] , the reason for inconsistent findings of different studies in the empirical literature is using various economic approaches and functional patterns in different time and cases of countries [18] [19] [20] [21] . In a similar manner, as [22] [23] point out, the findings developed through Granger causality and results of contacted co-integration tests may easily change and differ by the used period and the details of the developed model. From the point of this argument, one may suppose that the estimations developed by time series may become invalid due to energy crises, such as increases in oil prices and momentary alterations arising from business cycles as a result of possible structural changes or interruptions in energy consumption series. Also, it is possible to assume that these structural breaks demonstrate that energy consumption is non- linear. Certain studies examine these breaks such as [17] [23] - [31] . Correspondingly, one may suggest that there is a non-linear the relation between energy prices and/or energy consumption and economic variables as [32] - [38] stress on.
As such, certain studies prefer to use not only linear but also non-linear Granger causality models such as [24] . This study uses nonlinear Granger causality models depending on the studies of [39] and [40] to examine the causality between energy consumption and output in eight Asian countries along with the United States. The findings indicate that a non-linear causal nexus between energy consumption and output is valid in the case of Taiwan, Hong Kong, Singapore, Indonesia and Philippines; whereas, in the pattern of United States, South Korea and Thailand there is no supportive evidence for causality. [31] examine nonlinear Granger causality tests, proposed by [39] [41] for G7 countries. Their results are conflicting and country-specific. Using the same method [42] finds supportive evidence for the growth hypothesis in the case of Greece, [43] verify the neutrality hypothesis for Turkey.
However, other studies concentrate on non-linear vector error correction models such as [17] offering a nonlinear panel vector error correction test, which examines the data belong to G7 countries for the period between 1977 and 2007. In this study, they design a panel co-integration test for a non-linear transition relapse scheme, and they have found a certain sign of co-integration between energy consumption and growth in the economy. Using a smooth transition vector autoregressive model, [30] analyze non-linear dynamic nexus between energy use and output in Turkey for the period of 1960-2010. The impulse-responses functions suggest that negative and positive energy shocks asymmetrically affect output growth. Furthermore, they find asymmetry in the big versus small negative energy shocks and small versus big positive output shocks, no asymmetry in the effects of big versus small positive energy shocks and negative output shocks.
[23] tests the causal nexus between the use of energy and GDP in the United States for the period 1960-2005, employing Markov-switching vector autoregressive models. Results from the model show evidence of bi-directional Granger causality between the variables in the first regime, while there is no causality between the variables in the second regime. Another study, which focuses on the relation between volatility in energy consumption and uncertain variations in real GDP product in the United Kingdom, based on Markov regime-switching modeling perspective is conducted by [28] . By the findings developed through Markov regime-switching ARCH design, energy consumption volatility has no significant co-existing and contemporaneous relation with Gross Domestic Product in the first (low-volatility) regime, however, in the second (high-vola- tility) regime there is an important positive relation between GDP volatility and energy usage volatility. [29] , apply the momentum-threshold autoregressive (M- TAR) co-integration method to examine the long-term equilibrium relationship between the growth of output and energy use, The results indicate that there is a nonlinear cointegration relationship between energy consumption and GDP except the residential sector in Taiwan.
3. Data and Modeling Strategy
The criticism of linearity of the classical cointegration model suggested by [44] leads to attempts at modeling of non-linear cointegration relation. Therefore, the contributions in [45] - [57] provide important contributions that change approaches and the understanding of the idea of cointegration and error correction modeling. As a result, they put forth the main argument that linear models are too restrictive. For instance, linear models have a symmetry feature which implies that shocks occurring in a recession phase are just as persistent as shocks taking place in an expansion phase of business cycle fluctuations. Hence, linear models cannot adequately capture asymmetries that may exist in business cycles [58] . Since energy consumption and economic growth are parts of cyclical business fluctuations, linear models may be too restrictive in the case of the relationship between energy consumption and economic growth, as well.
Some authors try to deal with both non-stationarity and non-linearity in the co-integrating modeling strategy, since the mid-1990s. This extended section of co-integration research may be described as the primacy of three regime switching models. The first one is the threshold error correction model developed by [51] . The Markov-switching error correction model of [59] is the second regime switching model. The last model is the smooth transition errorcorrectionmodel developed by [60] . The development of this literature reflects a general consideration that the assumption of linear adjustment may be excessively restrictive in a wide range of economically interesting situations. However, the majority of these studies are built on another overly restrictive assumption that the long-run relationship may be represented as a symmetric linear combination of non-sta- tionary stochastic regressors.
Alternatively, [61] has suggested the bivariate asymmetric cointegrating regression of unemployment on output, where output is decomposed into partial sum processes of positive and negative changes. By this piecewise linear specification, he finds that the impact of recessionary innovation on unemployment is larger in absoluteterms than that of cyclical upturns, indicating a hysteretic relationship. Furthermore, [62] develop the notion that the co-integrating relationship may be defined between the positive and negative components of the underlying variables, an effect which they term “hidden co-integration”.
Lastly, [16] develop a simple and flexible nonlinear dynamic framework capable of simultaneously and coherently modeling asymmetries both in the underlying long-run relationship and in the patterns of dynamic adjustment. They derive the dynamic error correction representation associated with the asymmetric long-run cointegrating regression, resulting in the nonlinear autoregressive distributed lag model. Moreover, following [63] [64] , they employ a pragmatic boundstesting procedure for the existence of a stable long-run relationship which is valid irrespective of whether the underlying regressors are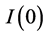 ,
, 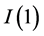 or mutually co-integrated.
or mutually co-integrated.
The non-linear autoregressive distributed lag model suggested by [16] use negative and positive components of the independent variable to investigate the long-run relationship between two variables, as defined by [62] . A simple asymmetric long-run regression model can be built as Equation (1).
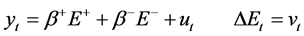 (1)
(1)
where 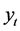 and
and 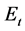 are real logarithmic GDP and logarithmic energy consumption (as Btu), respectively. Real GDP is obtained from the OECD database, and E is taken from US Energy Information Agency. The data set is composed of quarterly data covering the period between 1973:1 and 2013:4. Both variables are seasonally adjusted. The variables are scalar and
are real logarithmic GDP and logarithmic energy consumption (as Btu), respectively. Real GDP is obtained from the OECD database, and E is taken from US Energy Information Agency. The data set is composed of quarterly data covering the period between 1973:1 and 2013:4. Both variables are seasonally adjusted. The variables are scalar and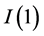 .
. 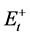 and
and 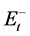 are obtained by partially summing of positive and negative changes in
are obtained by partially summing of positive and negative changes in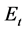 , depicted as Equation (2).
, depicted as Equation (2).
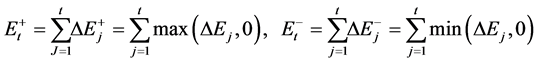 (2)
(2)
If Equation (1) is estimated with OLS estimator to calculate the cointegration parameter, some important problems such as weak endogeneity and serially correlated errors can arise. So, estimated cointegrating parameter would be poorly determined especially in finite samples. The best solution to these problems may be the ARDL approach advanced by [63] [64] . The ARDL approach presents a flexible dynamic parametric framework to model long-run and short-run asymmetries. Hence, one can examine the following nonlinear ARDL (p, q) model to find details [16] :
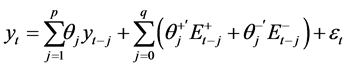 (3)
(3)
Following [64] , Equation (1) can be reformulated in the error correction form:
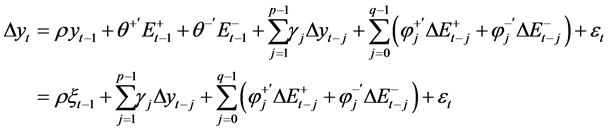 (4)
(4)
where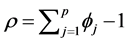 ,
,
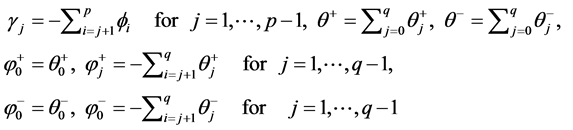 and
and
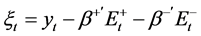 is the non-linear error correction term where
is the non-linear error correction term where 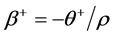 and
and 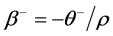 are the asymmetric long-run parameters.
are the asymmetric long-run parameters.
[16] make some rearrangements in Equation (4) to combine some desirable properties of the fully modified OLS and ARDL dynamic models. They reach the following conditional nonlinear error correction model:

Equation (5) can be estimated by standard OLS since the model is linear. Moreover, the null hypothesis of a symmetric long-run relationship 

The existence of an asymmetric cointegration relationship in non-linear error correction model can be tested using FPSS test suggested by [64] . The null hypothesis of FPSS test is
The model specification in Equation (5) is necessary for establishing the properties of the dynamic adjustment mechanism. There is no restriction on both short and long run asymmetries in Equation (5). Three alternative model specifications are possible in Equation (5). Firstly, short-run dynamic asymmetries can be analyzed in the response of economic growth to fluctuations in the energy consumption by implicitly imposing the long-run symmetry restrictions 

Second, an asymmetric long-run relation can be investigated by imposing short-run symmetry restriction 

Lastly, when one assumes both symmetric short-run and long-run adjustment, the most restrictive specification is obtained as Equation (8):

Following the boundstesting approach, the models can be estimated irrespective of whether 


4. Empirical Findings
The NARDL approach starts to distinguish negative and positive components of the energy consumption variable. Figure 1 depicts the total energy consumption and its negative and positive components.
Linear ARDL and asymmetric ARDL models were estimated to compare the two models. Firstly, we choose a lag specification for ARDL model, following the general-to-specific approach. The preferred specification is determined by starting with max p = 12 and max q = 8. Later, all insignificant stationary regressors are dropped from the ARDL model. In Table 1, empirical findings of linear dynamicmodel (Equation (8)) estimation are represented.
According to Table 1, the cointegration test (FPSS) cannot reject the null hypothesis of no co-integrating relationship between energy consumption and economic growth in the symmetric ARDL model. Furthermore, the normality test (



Figure 1. Total energy consumption (a) and its positive (b) and negative (c) components.
nexus between energy consumption and economic growth. So, asymmetric ARDL modeling may be a more correct modeling strategy than linear ARDL
Table 1. Results of linear ARDL model estimation.
Note: E represents the natural logarithm of energy consumption.







approach. Since we cannot know the true model specifications, the estimated ARDL model includes both short term and long term asymmetries. Table 2 presents the findings of asymmetric ARDL model estimation.
In Table 2, the WALDLR is the Wald test which has the null hypothesis of long-run symmetry (




In the next stage of the analyses, impulse response function for the relationship between energy consumption and economic growth is investigated. An impulse response function measures the time profile of the effect of a shock on the behavior of a series. Like that, one can approve an impulse response function as the outcome of a conceptual experiment. The time profile of the effect of a positive unit shock hitting a series at time t can be conceptualized as a simulation. The idea closely resembles Keynesian multiplier analysis. The distinction between the two is that the impulse response function analyzesare carried out on
Table 2. Results of asymmetric ARDL model estimation.
Note: E represents the natural logarithm of energy consumption.





shocks or innovations of macroeconomic time series, rather than the series themselves, such as investment or government expenditure [64] .
Although we find that the optimal model requires long termasymmetry and short term symmetry specifications, for the aim of comparison, impulse response functions are graphed by estimating an unconstrained and three constrained models. The unconstrained model in Equation (5) allows asymmetries both in the short run and long run (Figure 2(a)). Equation (6) allows asymmetry in the short run but not in the long run (Figure 2(c)). Imposing the short run symmetry restriction in Equation (7), we reach the long term asymmetry (Figure 2(b)). Lastly, the symmetry restrictions are imposed both in the long run and short run in Equation (8) (Figure 2(d)).
The Figure 2(a) and Figure 2(b) are similar since both assume asymmetry in the long run. The figures depict that the effect of a positive and negative change in energy consumption on economic growth are highly different. The cumulative effect of positive change in energy consumption increases nearly for 20 quarters. In later periods it does not change. However, after the cumulative effect of a negative change in energy consumption on economic growth increases during the first 8 quarters, the negative effect dies off for approximately the consecutive
Figure 2. Cumulative effect of energy consumption on economic growth. (a) Short-term and long-term asymmetry; (b) Short-term symmetry and long-term asymmetry; (c) Long-term symmetry and short-term asymmetry; (d) Short-term and long-term symmetry.
12 quarters. The cumulative negative effect of a decrease in energy consumption on economic growth disappears after about 20 quarters.
Figure 2(c) artificially, indicates that long term symmetry restriction leads to reduce the cumulative effect of an increase in energy consumption on economic growth. Even if long term symmetry is assumed, due to the short term asymmetry, long run asymmetry does not disappear in 80 quarters. Since Equation (8) is misspecified, Figure 2(d) illustrates the same effects of negative and positive changes in energy consumption on economic growth regarding the absolute value.
5. Concluding Results
A large number of studies in the literature seek to find a proper modeling strategy that captures true dynamic relationship between energy consumption and economic growth. Specification errors in the models lead to findings and policy suggestions incompatible with real policy implementations. For example, the papers, finding evidence in favor of the growth hypothesis, suggest stopping energy saving policies, since a decrease in energy consumption does harm economic growth. However, this policy suggestion conflicts the real life fact of the societies continuous strive towards new ways to reduce energy consumption, be it at the individual, firm or country level. These efforts at improved energy efficiency can be in the form of a new technological achievement such as an electrical automobile, high efficiency motors, replacement of energy losing machines, or organizational rearrangements such as regulating the working hours, developing an efficient energy saving strategy and mandatory regulation for improving energy efficiency. So, one can be doubtful about modeling strategy leading to the suggestion of stopping energy saving policy.
Departing from previous studies in the literature, we assume that the relationship between energy consumption and economic growth is both dynamic and asymmetric. To apply this modeling strategy, we follow the asymmetric ARDL approach suggested by [16] . The findings indicate that energy consumption asymmetrically affects the economic growth in the long run but not in the short run. Furthermore, the long run coefficient of a negative component of energy consumption is too small and statistically insignificant even at 10% level. So, over the long term the effect of a decrease in energy consumption on economic growth may be reduced by the dimmer effect of energy saving policies such as technological progress or organizational rearrangement. The long run coefficient of positive element of energy consumption is found about 0.9 and statistically significant at 1% level. Therefore one may conclude that the effect of an increase in energy consumption on economic growth may be raised by the booster effect of energy saving policies.
The overall assessment of the analysis in this study is that energy saving policy option is independent of the relationship between energy consumption and economic growth. More precisely, energy saving policy may have a positive effect on economic growth rather than negative effect. That is, energy saving policy should be followed in every scenario to reduce the cost of energy and environmental pollution.
Cite this paper
Bayramoglu, A.T. and Yildirim, E. (2017) The Relationship between Energy Consumption and Economic Growth in the USA: A Non-Linear ARDL Bounds Test Approach. Energy and Power Engineering, 9, 170-186. https://doi.org/10.4236/epe.2017.93013
References
- 1. Stiglitz, J.E. (1974) Growth with Exhaustible Natural Resources: Efficient and Optimal Growth Paths. The Review of Economic Studies, Symposium on the Economics of Exhaustible Resources, 41, 123-138. https://doi.org/10.2307/2296377
- 2. Solow, R.M. (1974) The Economics of Resources or the Resources of Economics. The American Economic Review, 64, 1-14. https://doi.org/10.1057/9780230523210_13
- 3. Dasgupta, P. and Heal, G. (1974) The Optimal Depletion of Exhaustible Resources. Review of Economic Studies, Symposium on the Economics of Exhaustible Resources, 41, 3-28. https://doi.org/10.2307/2296369
- 4. Stern, D.I. and Cleveland, C.J. (2004) Energy and Economic Growth. Rensselaer Working Paper in Economics No.0410. Rensselaer Polytechnic Institute, Troy, NY.
- 5. Bartleet, M. and Gounder, R. (2010) Energy Consumption and Economic Growth in New Zealand: Results of Trivariate and Multivariate Models. Energy Policy, 38, 3508-3517.
- 6. Stern, D.I. (1997) Limits to Substitution and Irreversibility in Production and Consumption: A Neoclassical Interpretation of Ecological Economics. Ecological Economics, 21, 197-215.
- 7. Cleveland, C.J., Costanza, R., Hall, C.A.S. and Kaufmann, R. (1984) Nergy and the U.S. Economy: A Biophysical Perspective. Science, 225, 890-897. https://doi.org/10.1126/science.225.4665.890
- 8. Hall, C.A.S., Cleveland, C.J. and Kaufmann, R. (1986) Energy and Resource Quality: The Ecology of the Economic Process. Wiley InterScience, New York.
- 9. Hall, C., Tharakan, P., Hallock, J., Cleveland, C. and Jefferson, M. (2003) Hydrocarbons and the Evolution of Human Culture. Nature, 426, 318-322. https://doi.org/10.1038/nature02130
- 10. Apergis, N. and Tang, C.F. (2013) Is the Energy-Led Growth Hypothesis Valid? New Evidence from a Sample of 85 Countries. Energy Economics, 38, 24-31.
- 11. Brookes, L. (1990) The Greenhouse Effect: The Fallacies in the Energy Efficiency Solution. Energy Policy, 18, 199-201.
- 12. Khazzoom, J.D. (1980) Economic Implications of Mandated Efficiency Standards for Household Appliances. The Energy Journal, 1, 21-40.
- 13. Saunders, H.D. (1992) The Khazzoom-Brookes Postulate and Neoclassical Growth. The Energy Journal, 13, 131-148. https://doi.org/10.5547/ISSN0195-6574-EJ-Vol13-No4-7
- 14. Greening, L.A., Greene, D.L. and Difiglio, C. (2000) Energy Efficiency and Consumption—The Rebound Effect—A Survey. Energy Policy, 28, 389-401.
- 15. Howarth, R.B. (1997) Energy Efficiency and Economic Growth. Contemporary Economic Policy, 15, 1-9. https://doi.org/10.1111/j.1465-7287.1997.tb00484.x
- 16. Shin, Y., Yu, B. and Greenwood-Nimmo, M. (2014) Modeling Asymmetric Cointegration and Dynamic Multipliers in a Nonlinear ARDL Framework. In: Horrace, W.C. and Sickles, R.C., Eds., Festschrift in Honor of Peter Schmidt: Econometric Methods and Applications, Springer Science & Business Media, New York, 281-314. https://doi.org/10.1007/978-1-4899-8008-3_9
- 17. Omay, T., Hasanov, M. and Ucar, N. (2012) Energy Consumption and Economic Growth: Evidence from Nonlinear Panel Cointegration and Causality Tests. Munich Personal RePEc Archive, MPRA Paper No. 37653.
- 18. Soytas, U. and Sari, R. (2003) Energy Consumption and GDP: Causality Relationship in G7 Countries and Emerging Markets. Energy Economics, 25, 33-37.
- 19. Ozturk, I. (2010) A Literature Survey on Energy-Growth Nexus. Energy Policy, 38, 340-349.
- 20. Balcilar, M., Ozdemir, Z.A. and Arslanturk, Y. (2010) Economic Growth and Energy Consumption Causal Nexus Viewed through a Bootstrap Rolling Window. Energy Economics, 32, 1398-1410.
- 21. Costantini, V. and Martini, C. (2010) The Causality between Energy Consumption and Economic Growth: A Multi-Sectoral Analysis Using Non-Stationary Cointegrated Panel Data. Energy Economics, 32, 591-603.
- 22. Lee, C.C. (2006) The Causality Relationship between Energy Consumption and GDP in G-11 Countries Revisited. Energy Policy, 34, 1086-1093.
- 23. Fallahi, F. (2011) Causal Relationship between Energy Consumption (EC) and GDP: A Markov-Switching (MS) Causality. Energy, 36, 4165-4170.
- 24. Chiou-Wei, S.Z., Chen, C.F. and Zhu, Z. (2008) Economic Growth and Energy Consumption Revisited—Evidence from Linear and Nonlinear Granger Causality. Energy Economics, 30, 3063-3076.
- 25. Huang, B.N., Hwang, M.J. and Yang, C.W. (2008) Does More Energy Consumption Bolster Economic Growth? An Application of the Nonlinear Threshold Regression Model. Energy Policy, 36, 755-767.
- 26. Narayan, P.K. and Smyth, R. (2008) Energy Consumption and Real GDP in G7 Countries: New Evidence from Panel Cointegration with Structural Breaks. Energy Economics, 30, 2331-2341.
- 27. Esso, L.J. (2010) Threshold Cointegration and Causality Relationship between Energy Use and Growth in Seven African Countries. Energy Economics, 32, 1383- 1391.
- 28. Rashid, A. and Kocaaslan K.O. (2013) Does Energy Consumption Volatility Affect Real GDP Volatility? An Empirical Analysis for the UK. International Journal of Energy Economics and Policy, 3, 384-394.
- 29. Hu, J.-L. and Lin, C.-H. (2013) Examining Asymmetric Behavior between Energy Consumption and Economic Growth in Taiwan. Energy Sources, Part B: Economics, Planning, and Policy, 8, 76-85. https://doi.org/10.1080/15567240903160922
- 30. Arac, A. and Hasanov, M. (2014) Asymmetries in the Dynamic Interrelationship between Energy Consumption and Economic Growth: Evidence from Turkey. Energy Economics, 44, 259-269.
- 31. Ajmi, A.N., Montasser, G.E. and Nguyen, D.K. (2013) Testing the Relationships between Energy Consumption and Income in G7 Countries with Nonlinear Causality tests. Economic Modeling, 35, 126-133.
- 32. Mork, K.A. (1989) Oil and the Macroeconomy When Prices Go up and down: An Extension of Hamilton’s Results. Journal of Political Economy, 97, 740-744. https://doi.org/10.1086/261625
- 33. Lee, K., Ni, S. and Ratti, R.A. (1995) Oil Shocks and the Macroeconomy: The Role of Price Variability. The Energy Journal, 16, 39-56. https://doi.org/10.5547/ISSN0195-6574-EJ-Vol16-No4-2
- 34. Hamilton, J.D. (1996) This Is What Happened to the Oil Price-Macroeconomy Relationship. Journal of Monetary Economics, 38, 215-220.
- 35. Davis, S., and Haltiwanger, J. (2001) Sectoral Job Creation and Destruction Responses to Oil Price Changes. Journal of Monetary Economics, 48, 465-512.
- 36. Aloui, C. and Jammazi, R. (2009) The Effects of Crude Oil Shocks on Stock Market Shifts Behavior: A Regime Switching Approach. Energy Economics, 31, 789-799.
- 37. Gabreyohannes, E. (2010) A Nonlinear Approach to Modeling the Residential Electricity Consumption in Ethiopia. Energy Economics, 32, 515-523.
- 38. Rahman, S. and Serletis, A. (2010) The Asymmetric Effects of Oil Price and Monetary Policy Shocks: A Nonlinear VAR Approach. Energy Economics, 32, 1460-1466.
- 39. Hiemstra, C. and Jones, J.D. (1994) Testing for Linear and Non-Linear Granger Causality in the Stock Price-Volume Relation. The Journal of Finance, 49, 1639- 1664.
- 40. Baek, E.G. and Brock, A.W. (1992) A General Test for Non-Linear Granger Causality: Bivariate Model. Technical Report, Korean Development Institute and University of Wisconsin-Madison.
- 41. Kyrtsou, C. and Labys, W.C. (2006) Evidence for Chaotic Dependence between US Inflation and Commodity Prices. Journal of Macroeconomics, 28, 256-266.
- 42. Dergiades, T., Martinopoulos, G. and Tsoulfidis, L. (2013) Energy Consumption and Economic Growth: Parametric and Non-Parametric Causality Testing for the Case of Greece. Energy Economics, 36, 686-697.
- 43. Nazlioglu, S., Kayhan, S. and Adiguzel, U. (2014) Electricity Consumption and Economic Growth in Turkey: Cointegration, Linear and Nonlinear Granger Causality. Energy Sources, Part B: Economics, Planning, and Policy, 9, 315-324. https://doi.org/10.1080/15567249.2010.495970
- 44. Engle, R.F. and Granger, C.W.J. (1987) Cointegration and Error Correction: Representation, Estimation and Testing. Econometrica, 55, 251-276. https://doi.org/10.2307/1913236
- 45. Granger, C.W.J. and Lee, T.-H. (1989) Investigation of Production, Sales and Inventory Relationships Using Multicointegration and Non-Symmetric Error Correction Models. Journal of Applied Econometrics, 4, 145-159. https://doi.org/10.1002/jae.3950040508
- 46. Granger, C.W.J. and Hallman, J.J. (1991) Nonlinear Transformations of Integrated time Series. Journal of Time Series Analysis, 12, 207-224. https://doi.org/10.1111/j.1467-9892.1991.tb00078.x
- 47. Granger, C.W.J. (1995) Modeling Nonlinear Relationships between Extended Memory Variables. Econometrica, 63, 265-279.
- 48. Granger, C.W.J. (1997) On Modeling the Long Run in Applied Economics. Economic Journal, 107, 169-177.
- 49. Granger, C.W.J. and Swanson, N.R. (1996) Further Developments in the Study of Cointegrated Variables. Oxford Bulletin of Economics and Statistics, 58, 537-553. https://doi.org/10.1111/j.1468-0084.1996.mp58003007.x
- 50. Gregory, A.W. and Hansen, B.E. (1996) Residual Based Tests for Cointegration in Models with Regime Shifts. Journal of Econometrics, 70, 99-126.
- 51. Balke, N.S. and Fomby, T.B. (1997) Threshold Cointegration. International Economic Review, 38, 627-645. https://doi.org/10.2307/2527284
- 52. Siklos, P.L. and Granger, C.W.J. (1997) Regime-Sensitive Cointegration with an Application to Interest-Rate Parity. Macroeconomic Dynamics, 1, 640-657. https://doi.org/10.1017/S1365100597004057
- 53. Aparicio, F.M. and Escribano, A. (1998) Information-Theoretic Analysis of Serial Dependence and Cointegration. Studies in Nonlinear Dynamics and Econometrics, 3, 119-140. https://doi.org/10.2202/1558-3708.1044
- 54. Enders, W. and Granger, C.W.J. (1998) Unit-Root Tests and Asymmetric Adjustment with an Example Using the Term Structure of Interest Rates. Journal of Business & Economic Statistics, 16, 304-311.
- 55. Escribano, A. and Pfann, G.A. (1998) Non-linear Error Correction, Asymmetric Adjustment and Cointegration. Economic Modeling, 15, 197-216.
- 56. Enders, W. and Siklos, P.L. (2001) Cointegration and Threshold Adjustment. Journal of Business & Economic Statistics, 19, 166-176. https://doi.org/10.1198/073500101316970395
- 57. Park, J.Y. and Phillips, P.C.B. (2001) Nonlinear Regressions with Integrated Time Series. Econometrica, 69, 117-161. https://doi.org/10.1111/1468-0262.00180
- 58. Koop, G., Pesaran, M.H. and Potter, S.M. (1996) Impulse Response Analysis in Nonlinear Multivariate Models. Journal of Econometrics, 74, 119-147.
- 59. Psaradakis, Z., Sola, M. and Spagnolo, F. (2004) On Markov Error-Correction Models with an Application to Stock Prices and Dividends. Journal of Applied Econometrics, 19, 69-88. https://doi.org/10.1002/jae.729
- 60. Kapetanios, G., Shin, Y. and Snell, A. (2006) Testing for Cointegration in Nonlinear Smooth Transition Error Correction Models. Econometric Theory, 22, 279-303. https://doi.org/10.1017/S0266466606060129
- 61. Schorderet, Y. (2001) Revisiting Okun’s Law: An Hysteretic Perspective. University of California, Mimeo, San Diego.
- 62. Granger, C.W.J. and Yoon, G. (2002) Hidden Cointegration. Department of Economics Discussion Paper 2002-02, University of California, San Diego. https://doi.org/10.2139/ssrn.313831
- 63. Pesaran, M.H. and Shin, Y. (1998) An Autoregressive Distributed Lag Modeling Approach to Cointegration Analysis. In: Strom, S., Ed., Econometrics and Economic Theory: The Ragnar Frisch Centennial Symposium, Cambridge University Press, Cambridge, 371-413. https://doi.org/10.1017/CCOL0521633230.011
- 64. Pesaran, M.H., Shin, Y. and Smith, R.J. (2001) Bounds Testing Approaches to the Analysis of Level Relationships. Journal of Applied Econometrics, 16, 289-326. https://doi.org/10.1002/jae.616



