Energy and Power Engineering
Vol.07 No.03(2015), Article ID:54806,9 pages
10.4236/epe.2015.73007
Unconventional Shale Reservoir’s Property Estimation through Modeling, Case Studies of Australian Shale
Robert Shiver*, Kim Nelsen, Eifei Li, John Lee, Grad Dwithes
Cooper Clean Energy Inc., Sydney, Australia
Email: *robert.shiver74@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 February 2015; accepted 14 March 2015; published 18 March 2015
ABSTRACT
A simplified approach is introduced to model production from shale gas resources. In this approach, a multi-fractured horizontal gas well in a shale formation is divided into four zones. Shale formation between each pair of hydraulic fractures consists of four zones: compacted zone around well-bore (1), shale matrix (2), induced fractures (3) and main hydraulic fractures (4). The main contribution of this study is considering varying permeability for each specific zone implemented in the mathematical presentation of gas flow in shale. Further, gas desorption and slippage effect are applied to the model to capture the realistic gas flow in shale. The nonlinear partial differential equation of gas flow obtained from mass conservations law is then solved numerically for each specific zone with respect to their appropriate boundary conditions. This approach then is applied to three case studies, Cooper Basin, Georgina and Galilee shale. A history matching of the mentioned formations is accomplished to find the most uncertain parameters undertaken through this simplified approach. Results of this study are in an agreement with other methods and it is demonstrated that the simplified approach provides more accurate production forecast for the well- established Georgina asset and is in a good agreement for Cooper and Galilee. This study is also valuable since it provides some rough estimation for shale rock characteristics as the basis for rigorous simulation studies.
Keywords:
Future Production, Shale Modeling, Hydraulic Fracturing, Physical Phenomena

1. Introduction
Gas shales are known for their ultra-low permeability, porosity and existence of significant amount of kerogen. Also, shale resources typically serve as both reservoir rock and source rock due to its rock surface kerogen that desorbs methane. Shale is a fine-grained sedimentary rock, which is comprised of consolidated clay-sized particles (DOE, 2009). Increased growth of natural gas production from shale gas reservoirs is due to the successful application and advances obtained in horizontal drilling and multi-stage hydraulic fracturing technologies. As a result of hydraulic fracturing, reasonable connectivity between horizontal wellbore and shale formation is gained that tied with the pre-existing network of natural fractures to enable gas production in an economic level. According to a recent report released by Energy Information Administration (EIA, 2014), increased cumulative dry gas production from 2012 to 2014 in shale gas assets reflect rapid growth of dual application of horizontal drilling and hydraulic fracturing. In the consequent paragraphs the general characteristics of major shale gas reservoirs in Australia is discussed, as they are shown in Figure 1. Afterwards, a brief description about state of the art of modeling the shale gas reservoirs along with an explanation about procedure to accomplish the objectives of this paper is provided.
The Cooper Basin is the most important on-shore petroleum and natural gas deposits in Australia. The oil and gas window is located 1250 m below the surface and was originally discovered in the 1960s (although there are larger oil and gas deposits off-shore). The first commercial discovery of gas occurred in 1963. It includes Australia’s largest onshore oil field, the Jackson oil field. This field was discovered in 1981. Pipelines transport gas to the major markets of Brisbane, Adelaide and Sydney. Overall about 1800 petroleum wells have been drilled. The Georgina Basin is a large (ca. 330,000 km2) intracratonic sedimentary basin in central and northern Australia, lying mostly within the Northern Territory and partly within Queensland. It is named after the Georgina River which drains part of the basin. Deposition of locally up to ca. 4 km of marine and non-marine sedimentary rocks took place from the Neoproterozoic to the late Paleozoic (ca. 850 - 350 Ma). Along with other nearby sedimentary basins of similar age (Amadeus Basin, Officer Basin), the Georgina Basin is believed to have once been part of the hypothetical Centralian Superbasin, that was fragmented during episodes of tectonic activity. The Galilee Basin is a permian geological basin in the western Queensland region of Australia. It is located west of the Surat Basin and is part of the Great Artesian Basin drainage basin. Towns close to proposed mines in the basin include Alpha and Jericho but the basin extends north past Hughenden, south to Charleville and west beyond Winton to Middleton (Department of Primary Industries and Resources SA).
The major challenge of production from unconventional reservoirs are due to extremely low porosity and permeability that are currently unlocked and resolved with advances gained by industry in multi-stage hydraulic fracturing technology but still these reservoirs have decent amount of complexity to be modeled per existence of
Figure 1. Unconventional resource basin in Australia.
various pressure dependent phenomena in both fluid and rock characteristics. Researchers are developed analytical and numerical approaches to model production form this complex rock that has advantages and disadvantages as follows. Analytical models simply overlook the complex physics of shale rock such as desorption or Klinkenberg effect but are very fast and powerful for decision making processes. Numerical approaches and commercial reservoir simulators consider the conventional methods to use for unconventional reservoirs that consider some aspects such as non-Darcy flow and desorption but the results of these approaches do not respond to the changes complex physics and the best results are gained when the mentioned physics are ignored that is again a conventional method of looking at shale that still is not acceptable and requires more work to meet the standards of industry.
Scientists [1] developed a simple yet powerful model for unconventional gas reservoirs that considered three zones for a hydraulically fractured horizontal well. They took the governing equations (partial differential equations) of gas flow to Laplace domain and dealt with ordinary equations and solved them in the new domain and used Stephest method to return to time domain. Two major disadvantages of their model are, first, as they look at the short term production with a well test pint of view to find shale rock characteristics and second, they did not consider surface desorption in their model that plays an important role in production form shale. In this regard, [2] [3] extended their model and improved the analytical solution to account and analyze the long-term production scenario of shale formation. Some researchers [4] [5] used the numerical techniques to model different aspects of shale production. However, they have used different tricks to account for complex physics of shale that may not be appropriate in some regards even though the results of their approaches are in good agreement with real field data. It is essential to account for different physics of shale in a direct procedure instead of using indirect methods as it is done with numerical techniques.
A researcher [6] introduced an integrated Trizone model that accounted for several existing pressure-depen- dent phenomena in shale unconventional gas reservoirs. They discovered that the minimum ingredient to accurately model the shale formations are considering desorption and pressure-dependent permeability of shale rock. They also investigated the effect of these physics of long-term production of shale assets. They considered advanced numerical methods to solve nonlinear partial differential equations brought by considering different phenomena fully implicitly. Further, they estimated some important rock parameters for Marcellus shale that is used in this paper for first try before history matching of three major shale assets in the Australia. This paper is an extension of their work by considering one more zone of interest to their model that play significant role in production form unconventional shale reservoirs. Detail of each zone introduced in this paper is explained in detail in the next section.
The focus of this work is to provide a simple approach to model unconventional reservoirs simultaneously accounting for the known physics and their effects on long-term production and ultimately estimating the uncertainties of our model through history matching of real production data of three major Australian shale formations. Nonlinearities achieved in governing equations due to considering several shale rock and fluid physics are solved with fully implicit methods. The numerical errors and stability criteria are perfectly taken care of and resolved accordingly. It is concluded that ignoring these physics form the modeling procedures of shale formations leads in over or under estimation of production.
2. Reservoir Flow Model
Natural fractures along with the primary hydraulic fractures are considered the main conduits for natural gas to flow to the wellbore and ultimately to well production. Accurate modeling of the natural fractures is very time consuming and almost an impossible since they exist all over the shale formation and their exact locations are unknowns. Advances in microseismic will guide toward locating these natural fracture that slip in the formation but not all the natural fractures. However, for each shale formation, the complexities of the natural fractures and their contribution to the production are not well established. Hydraulic fractures are considered as lanner plates with the permeabilities ranging from 2 md to 10 md for various shale formations [7] . With this assumption, modeling hydraulic fractures perpendicular across the horizontal wellbore is considered the straightest procedure in the literature. In this paper, seven hydraulic fractures are placed on the horizontal wellbore or all three shale formation case studies to keep similarities for comparison purposes.
Figure 2 demonstrates a horizontal well that own seven primary hydraulic fractures. It is assumed that production is supported from the rock equal as the height of shale formation and is adjustable for three case studies.
Figure 2. Unconventional resource basin in Australia.
Zone between each pair of primary hydraulic fractures is divided into four sections due to their different rock and fluid characteristics. Zone 1 is allotted to the region around wellbore that is highly compacted at the time of running hydraulic fracturing due to very high pressure slick water. It is assumed that natural fractures in is zone are fully closed and its conductivity is extremely low compared to other zones. Shale matrix that is not disturbed by any process is assigned to serve for zone 2. Natural fractures in this zone follow the cubic sugar model but the main difference is that in contrast with the cubic sugar model, here in this study, the conductivity of the natural fractures are pressure-dependent and are not treated constant. Shattered formation around primary hydraulic fractures is chosen for zone 3 that are assumed that are not filled with proppants as they are narrower than primary hydraulic fractures. Finally, primary hydraulic fractures are considered as zone 4. It is assumed that although this zone is filled with proppants but still the conductivity of this zone is pressure-dependent as the proppants tend to be compacted and loss their strength under stress.
Table 1 has itemized the specific characteristics of shale rock and different physics of shale fluid flow accounted in this model. The assumptions made to select different characteristics of shale rock and fluid is followed from the current literature. Several different combinations of these characteristics are possible that authors will approach them in their next study. Furthermore, Table 1 proposes nonlinearities affecting modeling shale formations as these physics and pressure-dependent parameters are all non-linear function added to the governing equations.
Zone I: The first zone is defined as the unstimulated shale rock in which hydrocarbon flows through the low permeable rock to enter the other zones. The fluid flow model in zone I incorporates variable permeability and gas desorption. Nonetheless, the slippage effect is not taken into account as this phenomenon dominates in high velocity regions near wellbore within hydraulic fractures.
Zone II: The second zone of the reservoir model is defined for induced-fractures around main hydraulic fractures. Unlike the first zone of the reservoir, the permeability of this section is pressure-sensitive and declines exponentially with the reservoir pressure. The sensitivity of permeability of this zone to pressure is higher than zone I and III since these zones are either cemented natural fractures or are filled up with proppants, respectively. The surface gas desorption and slippage effects on the permeability have been incorporated into the flow model in this zone. Schematic of zone II is shown in Figure 3.
Zone III: The third zone of the model includes the hydraulic fracture that are main paths for hydrocarbon that connect flow to the wellbore and consequently to production. Similar to zone I and II, the permeability of this
Table 1. Characteristics of each zone in the model.
Figure 3. Schematic of zones II and III.
section is pressure-sensitive and gradually declines exponentially as a function of the average reservoir pressure. Slippage effect is also considered into the flow model but no gas desorption has been assumed in hydraulic fractures.
3. Governing Equations and Physics of Flow in Shale
In order to evaluate well performance in a shale gas reservoir, it is important to understand, analyze, and correctly implement and integrate several physics of gas flow and interactions with rock into the model. In contrast to lessons learned from conventional gas reservoirs, the key success in shale modeling is coupling the interaction between fractures network and matrix while incorporating known physics in a right manner. This section introduces these physics and phenomena considering recent advances.
3.1. Mono and Multi-Layer Shale Rock Surface Gas Desorption
Large portion of shale rock consists of organic matter, kerogenic media. Natural gas methane molecules are adsorbed on the organic rich strata. Thus, significant amounts of natural gas can be produced from the surface of kerogen, which is also known as Total Organic Carbon, TOC [8] .
Langmuir [9] simply represents a nonlinear relationship between the potential amount of releasable-gas and the pore pressure. This equation represents that the potential amount of releasable-gas is just a function of reservoir pressure.
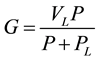 (1)
(1)
where G is the potential releasable-gas content in scf/ton, P is pore pressure in psi, and VL in scf/ton and PL in psi are Langmuir constants. Laboratory tests are necessary to determine VL and PL from core samples.
Another scientist introduced a multi-layer sorption model (BET) for gasses on solids which is a generalized form of [9]
The BET multiple-adsorbed-layer model is given by:
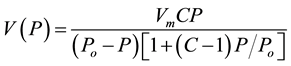 (2)
(2)
where V(P) is the gas volume of adsorption at pressure P, Vm is the maximum adsorption gas volume when the entire adsorbent surface being covered with a complete uni-molecular layer, Po is the saturation pressure of the gas, and C is a constant related to the heat of adsorption.
Parameters used in BET and Langmuir models are presented in Table 2.
3.2. Rock Compaction Effects
The permeability (or conductivity) of both hydraulic and natural fractures are easily influenced by changes of stress and strain during gas production from shale [10] which could strongly affect the productivity of producing wells. Therefore, incorporating pressure dependency of fractures permeability in reservoir modeling and simulation process is a significant step toward more realistic assessments of production behavior of shale reservoirs [11] .
Also, researcher [12] investigated the geo-mechanical properties of Marcellus shale. They generated a common source for securing these rock mechanical properties, geomechanical well logs, and studied various characteristics such as minimum horizontal stress, young, bulk shear modulus, as well as poison’s ratio that play an important role in defining the stress profiles of an unconventional reservoir. Moreover, having an access to rock’s geo-mechanical properties enhances the understanding of parameters, such as conductivity and pressure dependency of permeability [13] .
[14] conducted an experiment on Bakken shale rock samples and identified that other correlation given below is at most a practical relation that determines the pressure dependency of natural fractures. In this paper, we have incorporated Equation (3) to account for the pressure-dependency of permeability in zone II.
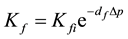 (3)
(3)
where 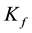 is fracture permeability,
is fracture permeability,  is initial fracture permeability,
is initial fracture permeability, 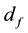 is exponential decay constant which is determined by experiments, and
is exponential decay constant which is determined by experiments, and  is average reservoir pressure minus initial reservoir pressure. The exponential decay constant is considered as given below:
is average reservoir pressure minus initial reservoir pressure. The exponential decay constant is considered as given below:
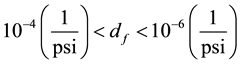 (4)
(4)
Equation (5) presents pressure dependency of permeability that is derived from experimental studies published by [15] [16] generated a conductivity multiplier chart based on their experimental data in order to implement in a commercial reservoir simulation. We used this table to express the relationship between permeability and pore pressure change with an exponential mathematical expression
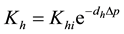 (5)
(5)
where 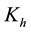 is hydraulic fracture permeability,
is hydraulic fracture permeability, 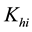 is initial hydraulic fracture permeability,
is initial hydraulic fracture permeability, 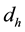 is exponential
is exponential
Table 2. Values used in BET and Langmuir isotherm models.
decay constant determined by experiments and 

3.3. Slippage Effect
The gas slippage known as Klinkenberg effect is very significant and might not be ignored while modeling shale gas flow. Klinkenberg effect, [17] presents a nonlinear relationship between absolute permeability and pore pressure given in Equation (6).

where 


3.4. Real Gas Properties
Shale gas reservoirs similar to other hydrocarbon reservoirs have very high temperature and pressure conditions. Physical behavior of natural gas is very nonlinear under such conditions and considering the ideal gas equation of state (EOS) results in an inaccurate evaluation of unconventional assets. Peng-Robinson (PR) EOS is used in this study and is incorporated and developed in the numerical scheme. A cubic equation of PR EOS is expressed by compressibility factor that is given by Equation (7).

where








ture and critical pressure of each component; 


For the viscosity of real gases, is applied to the model and Equation (9) is derived by Dempsey.

where 

pressed as a function of pressure, temperature and a series of correction coefficients; 

4. Governing Equations
Mass conservation law is applied to each zone for single phase flow of gas (Sg = 1). Gas material balance equation is established as below:
Equations (10) and (11) represent the mathematical expressions for each term in the above mass conservation law.



where ug is the velocity of gas, ρg is free gas density; ρgsc is the gas density in standard condition, G is potential releasable-gas content in scf/ton in Langmuir model, ρb is shale matrix density and ϕ is rock porosity. These terms are added up and shown below in Equation (12):

Initial condition for this study is, similar to the other reservoir modeling and simulation process, the initial reservoir pressure given in Equation (13). For all four zones, this condition is used to solve the governing equations.

The well production is calculated by Equation (14), production from one fracture and multiplied by the number of available hydraulic fractures to account for total production.

Mass balance equation and boundary conditions are presented in this section for each zone.
5. Estimation of Important Parameters for Three Shale Formations
In order to validate the accuracy of the proposed model, history matching of a single well with real field production data is accomplished. Three parameters of interest that tend to be more uncertain, in the proposed model, are determined and varied to achieve a reasonable history match. These parameters include, width of zone II, and the exponential decay value for zones II and III that are assumed to be the most influential in the modeling process using simple model proposed in this paper. Table 3 provides the final values associated with these three uncertain parameters.
It is observed that induced-fracture zone approximately extends up and varies for each shale asset which greatly contributes to cumulative gas production. This provides insights for operators using commercial reservoir simulators for adjusting the width in which local grid refinement should be considered in their attempt in running accurate modeling of their shale gas assets.
Table 3. Parameters determined for Cooper, Georgina and Galilee Basins.
6. Conclusions
This paper presents a simplified reservoir model for shale gas assets. The outcomes of our paper are outlined below.
Results of this study prove that the minimum requirements necessary to model shale gas reservoirs are: 1) desorption phenomena and 2) pressure-sensitive permeability for hydraulic and induced-fractures (zones II and III) into the flow governing equations. Consequently, it is unnecessary to add more mechanisms and nonlinearity into the model (in agreement to [3] [18] [19] ).
Pressure-sensitive hydraulic fracture (zone III) and induced-factures (zone II) are essential in the modeling of shale formations, since the impact of this geomechanics is much higher than that of other parameters and also the production is more sensitive to induced-fracture zone compared with hydraulic fractures.
Gas desorption for the organic rich material has greater impact at the later period of production compared with early production. Also, ultimate gas recovery is higher considering the desorption phenomena.
Moreover, as a result of history matching process, exponential decay constants for hydraulic fracture (III) and the induced-fracture (II) zones are determined, which gives a rough estimation of these two essential parameters in the simulation processes of Marcellus shale reservoir.
Our approach is simple, yet powerful for practical use and efficient for the coupling of known pressure-sen- sitive phenomena in shale gas reservoir modeling and provides further insights into our understandings of physics and mathematics behind the simulation of unconventional reservoirs.
References
- Brown, M.L. (2009) Analytical Trilinear Pressure Transient Model for Multiply Fractured Horizontal Wells in Tight Shale Reservors. M.Sc. Thesis, Colorado School of Mines, Golden.
- Aybar, U., Eshkalak, M.O., Sepehrnoori, K. and Patzek, T.W. (2014) Long Term Effect of Natural Fractures Closure on Gas Production from Unconventional Reservoirs. SPE Eastern Regional Meeting 2014, Charleston, 21-23 October 2014, Paper SPE 171010.
- Eshkalak, M.O., Aybar, U. and Sepehrnoori, K. (2014) An Integrated Reservoir Model for Unconventional Resources, Coupling Pressure Dependent Phenomena. Eastern Regional Meeting, Charleston, 21-23 October 2014, Paper SPE 171008.
- Civan, A.F., Devegowda, D. and Sigal, R. (2010) Accurate Simulation of Shale Gas Reservoir. Annual Technical Conference and Ehibition held in Florence, Italy, 19-22 September 2010, Paper SPE 135564.
- Eshkalak, M.O., Mohaghegh, S.D. and Esmaili, S. (2013) Synthetic, Geomechanical Logs for Marcellus Shale. Digital Energy Conference and Exhibition, The Woodlands, 5-7 March 2013, Paper SPE 163690.
- Eshkalak, M.O., Aybar, U. and Sepehrnoori, K. (2014) An Economic Evaluation on the Re-Fracturing Treatment of the US Shale Gas Resources. Eastern Regional Meeting, Charleston, 21-23 October 2014, Paper SPE 171009.
- Eshkalak, M.O., et al. (2014) Simulation Study on the CO2-Driven Enhanced Gas Recovery with Sequestration versus the Re-Fracturing Treatment of Horizontal Wells in the U.S. Unconventional Shale Reservoirs. Journal of Natural Gas Science and Engineering, 21, 1015-1024. http://dx.doi.org/10.1016/j.jngse.2014.10.013
- Mengal, S.A. and Wattenbarger, R.A. (2011) Accounting for Adsorbed Gas in Shale Gas Reservoirs. SPE Middle East Oil and Gas Show and Conference, Manama, 25-28 September 2011, Paper SPE 141085. http://dx.doi.org/10.2118/141085-MS
- Langmuir, I. (1918) The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. Journal of the American Chemical Society, 40, 1403-1461. http://dx.doi.org/10.1021/ja02242a004
- Tao, Q., Ghassemi, A. and Ehlig-Economides, C.A. (2010) Pressure Transient Behavior for Stress-Dependent Fracture Permeability in Naturally Fractured Reservoirs. CPS/SPE International Oil and Gas Conference and Exhibition, 8-10 June 2010, Beijing, SPE 131666.
- Eshkalak, M.O., Al-Shalabi, E.W., Aybar, U. and Sepehrnoori, K. (2014) Enhanced Gas Recovery by CO2 Sequestration versus Re-Fracturing Treatment in Unconventional Shale Gas Reservoirs. Abu Dhabi International Petroleum and Exhibition and Conference, Abu Dhabi, 10-13 November 2014, Paper SPE 172083.
- Omidvar Eshkalak, M. (2013) Synthetic Geomechanical Logs and Distributions for Marcellus Shale. M.Sc. Thesis, West Virginia University, Morgantown.
- Aybar, U. (2014) Investigation of Analytical Models Incorporating Geomechanical Effects on Production Performance of Hydraulically and Naturally Fractured Unconventional Reservoirs. M.Sc. Thesis, The University of Texas at Austin, Austin.
- Cho, Y., Ozkan, E. and Apaydin, O.G. (2013) Pressure-Dependent Natural-Fracture Permeability in Shale and Its Effect on Shale-Gas Well Production. SPE Reservoir Evaluation & Engineering, 16, 216-228. http://dx.doi.org/10.2118/159801-PA
- Alramahi, B. and Sundberg, M.I. (2012) Proppant Embedment and Conductivity of Hydraulic Fractures in Shales. The 46th US Rock Mechanics/Geomechanics Symposium, Chicago, 24-27 June 2012, ARMA 12-291.
- Aybar, U., Eshkalak, M.O., Sepehrnoori, K. and Patzek, T.W. (2014) The Effect of Natural Fracture’s Closure on Long-Term Gas Production from Unconventional Resources. Journal of Natural Gas Science and Engineering, 21, 1205-1213. http://dx.doi.org/10.1016/j.jngse.2014.09.030
- Klinkenberg, L.J. (1941) The Permeability of Porous Media To Liquids And Gases. API, Washington DC.
- Eshkalak, M.O., Mohaghegh, S.D. and Esmaili, S. (2014) Geomechanical Properties of Unconventional Shale Reservoirs. Journal of Petroleum Engineering, 2014, Article ID: 961641. http://dx.doi.org/10.1155/2014/961641
- Aybar, U., Yu, W., Eshkalak, M., Sepehrnoori, K. and Patzek, T.W. (2015) Evaluation of Production Losses from Unconventional Shale Reservoirs. Journal of Natural Gas Science and Engineering, 23, 509-516. http://dx.doi.org/10.1016/j.jngse.2015.02.030
NOTES
*Corresponding author.






