Energy and Power Engineering
Vol.06 No.11(2014), Article ID:50353,8 pages
10.4236/epe.2014.611029
Bootstrapped Multi-Model Neural-Network Super-Ensembles for Wind Speed and Power Forecasting
Zhongxian Men1,2, Eugene Yee2,3, Fue-Sang Lien1,2, Hua Ji1, Yongqian Liu4
1Waterloo CFD Engineering Consulting Inc., Waterloo, Ontario, Canada
2Department of Mechanical & Mechatronics Engineering, University of Waterloo, Waterloo, Onatrio, Canada
3Defence Research and Development Canada, Suffield Research Centre, Medicine Hat, Alberta, Canada
4School of Renewable Energy, North China Electric Power University, Beijing, China
Email: eyee0309@gmail.com
Copyright 2014 Her Majesty the Queen in Right of Canada. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.



Received 15 July 2014; revised 18 August 2014; accepted 4 September 2014
ABSTRACT
The bootstrap resampling method is applied to an ensemble artificial neural network (ANN) approach (which combines machine learning with physical data obtained from a numerical weather prediction model) to provide a multi-ANN model super-ensemble for application to multi-step- ahead forecasting of wind speed and of the associated power generated from a wind turbine. A statistical combination of the individual forecasts from the various ANNs of the super-ensemble is used to construct the best deterministic forecast, as well as the prediction uncertainty interval associated with this forecast. The bootstrapped neural-network methodology is validated using measured wind speed and power data acquired from a wind turbine in an operational wind farm located in northern China.
Keywords:
Artificial Neural Network, Bootstrap Resampling, Numerical Weather Prediction, Super-Ensemble, Wind Speed, Power Forecasting

1. Introduction
There has been an increasing emphasis towards a greater use of renewable energy (e.g., solar, wind, geothermal) as a strategy to reduce greenhouse gas emissions and to mitigate climate change. In this context, one of the fastest growing sources of renewable energy for the generation of “green electricity” is the power obtained from wind turbines. The ever increasing use of wind power poses new challenges. One important challenge is how to accommodate the unpredictable fluctuations in wind speed and direction which lead to variability and uncer- tainty in the wind power generation. The latter has significant implications for unit commitment and deter- mination of scheduling and dispatch decisions (economic dispatch) needed for the optimal utilization of wind energy within a mixed power system. In this regard, wind power forecasting has become a critical component in the efficient management of a green electrical power system (required by generation companies and utilities) and in electrical market operations (required by energy market analysts and traders).
The development of wind power forecasting models for improving the efficiency and reliability of mixed electrical power systems and for supporting electrical market operations has been reviewed by Costa et al. [1] , Ma et al. [2] and Foley et al. [3] . Methodologies for wind power forecasting can be categorized into three broad classes as follows: statistical, physical, and machine learning. Because time series of wind speed and power are frequently measured in the vicinity of wind farms, statistical approaches based on time series analysis and forecasting have been applied for the prediction of wind speed and power. Towards this purpose, time series forecasting based on the popular Box-Jenkins methodology [4] , as applied to autoregressive (AR) models, moving average (MA) models, and autoregressive moving average (ARMA) models, has been utilized for wind speed and power forecasting using historical time series of wind speed and power. As an example, Erdem and Shi [5] demonstrated the application of an ARMA model for wind speed and direction forecasting. More sophi- sticated nonlinear time series models that accommodate the temporal evolution of the variance (heteroskedas- ticity) such as the autoregressive conditional heteroskedasticity (ARCH) model by Engle [6] and the generalized autoregressive conditional heteroskedasticity (GARCH) models by Bollerslev [7] have been applied to describe the intrinsic variability in the wind speed and the associated generated power. For instance, the ARMA-GARCH and the GARCH-in-mean (GARCH-M) models proposed by Liu et al. [8] have been applied to model the mean and volatility of the wind speed.
The second general class of models is physically-based models for wind speed prediction based on numerical weather prediction (NWP) or computational fluid dynamics (CFD). Utilizing equations of physics such as the conservation principles of mass, momentum, and energy in conjunction with various parameterizations for sub- grid scale physical processes that cannot be resolved explicitly by the necessarily finite number of grid points that are used to represent the atmospheric flow, NWP and/or CFD models provide hydrodynamic and thermo- dynamic models of the atmosphere that can be used to furnish a prediction of the flow field in a prescribed region. The prediction of the wind velocity field can be used in conjunction with the power curve for a wind tur- bine to provide a generated power forecast. Numerical weather prediction models have a number of limitations, including limited spatial resolution resulting in a coarse representation of the local terrain [9] . To overcome the latter problem, Liu et al. [10] considered the possibility of coupling a synoptic scale flow model to a large-eddy simulation model for wind energy applications and Li et al. [11] recently introduced a short-term wind fore- casting methodology based on the use of CFD pre-calculated flow fields.
The third general class of models for wind power forecasting is based on machine learning approaches such as artificial neural networks, fuzzy systems, and support vector machines [3] [12] [13] . Unlike the parametric models used for time series forecasting, machine learning uses either a “gray” or “black” box (essentially non- parametric) representation for the underlying physical processes (defining a nonlinear mapping from an input to an output), and then utilizes various learning algorithms and historical time series of wind speed or power to “train” the gray (black) box. The black box trained in this manner can be applied subsequently to make pre- dictions of the future wind speed or generated power (from a wind turbine).
In this paper, we propose to use the bootstrap resampling method in conjunction with an ensemble artificial neural network (ANN) approach for the multi-step-ahead forecasting of wind speed and generated power. The artificial neural network combines machine learning with physical modeling by using NWP wind speed data from a physical model as the exogenous input to the network. The purpose of the bootstrap resampling method is to reduce the bias in prediction of the wind speed and power and to obtain more accurate estimates for the standard deviation (uncertainty) of these predictions. More importantly, the confidence bands in these pre- dictions can be determined, which can be used to provide a more rigorous uncertainty assessment in wind speed and power forecasting.
2. Bootstrapping Ensembles of Artificial Neural Networks
As discussed in the previous section, a major concern of wind energy management is the uncertainty quan- tification of multi-step-ahead predictions of the wind speed (at the turbine hub height) and the corresponding power generated by the turbine. Instead of choosing a single best ANN for forecasting, we propose instead to use the bootstrap resampling method in the context of an ensemble of ANNs for predictive uncertainty analysis.
Let
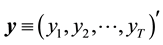 be a sample of realizations of a (scalar) random variable
be a sample of realizations of a (scalar) random variable , where the positive
, where the positive
integer
 represents the sample size and the
represents the sample size and the
 denotes the transpose of a vector (or matrix). In this paper,
denotes the transpose of a vector (or matrix). In this paper,
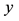 represents either the measured wind speed (at turbine hub height) or the power generated by a wind turbine. Similarly, let
represents either the measured wind speed (at turbine hub height) or the power generated by a wind turbine. Similarly, let
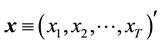 to be a sample of the corresponding predicted wind speed (at turbine hub height) obtained from a numerical weather prediction model. Finally, let
to be a sample of the corresponding predicted wind speed (at turbine hub height) obtained from a numerical weather prediction model. Finally, let
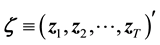 with
with
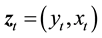 (
(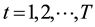 where
where
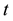 is the time step). Note that
is the time step). Note that
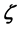 consists of the sample of collections of the measured wind speed (or power)
consists of the sample of collections of the measured wind speed (or power)
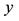 and the corresponding modeled wind speed
and the corresponding modeled wind speed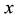 .
.
We want to first represent (model) the functional relationship between
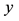 and
and
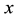 based on the training set
based on the training set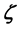 , by using an ensemble of artificial neural networks, and then employ all of the trained ANNs in the ensemble to forecast
, by using an ensemble of artificial neural networks, and then employ all of the trained ANNs in the ensemble to forecast
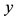 when new values of
when new values of

The nonlinear parameterized mapping




The output of the ANN is a continuous function of the input and


for the hidden layer and

for the output layer. In Equations (2) and (3), the index







Note that each neuron in the network is a unit that combines and processes all the data coming into the layer and then passes the transformed data (output of the activation function) to all the neurons of the successive layer. Specifically, the input of a neuron is a weighted sum of the outputs of all the neurons in the previous layer plus a bias. The weights








and the mean absolute error (MAE)

The minimization of these error functions is achieved using the particle swarm optimization algorithm [15] . Once an ANN has been trained, it can be used for the out-of-sample forecasting of the dependent (output) variable
To apply the bootstrap resampling procedure [16] to the ANN, we have to impose a statistical distribution on the sample data



















For each of these bootstrap samples, we can train an ensemble of ANNs with the same network architecture, but with each member of the ensemble having different numbers of neurons in the hidden layer (recall that the number of neurons in the input and output layers are determined a priori by the dimension of the input and output vectors, respectively). To be more specific, assume that the number of neurons in the hidden layer of the network architecture varies from











The procedure for bootstrapping an ensemble of neural networks is summarized as follows:
1. Assign the nonparametric distribution



2. Draw a (nonparametric) bootstrap sample (with replacement) from the empirical distribution function

and train







3. Repeat Step 2




We use a two-stage weighted averaging method to provide the predictive uncertainty assessment for the wind speed and power. For each bootstrap sample, we calculate the predictions (forecasts) of the multi-step-ahead wind speed and power using the



For each bootstrap sample,




which we denote as













where




Euclidean norm and


Once the weights









denoted by


(in-sample and multi-step-ahead) are given by


where


For a fixed bootstrap sample, the standard deviation vector

step-ahead prediction of





obtained from the ANN ensemble at the fixed time index

where



to obtain an unbiased estimator of the standard deviation.
At this point, we have





this purpose, we define another weight vector

evaluated similarly by minimizing an objective function similar to Equation (8), except now the error matrix is
constructed from the residuals between




calculated by using Equation (9). Once the weight vector



and the corresponding bootstrapped standard deviations from

where

computed in accordance to Equation (12).
Confidence intervals for the forecast of the output variable




with








3. Application of the Methodology
3.1. Data Preparation
The two data sets that we analyse were collected from a specific wind turbine, referred to as WT24 hereafter, located in a wind farm in northern China. One of these data sets corresponds to the hourly-averaged wind speeds measured at the turbine hub height and the other corresponds to the associated hourly-averaged power generated by the turbine. The wind speed and generated power time series, consisting of 432 observations each, were measured over a period of 18 days. The measurements collected over the first 15 days (corresponding to 83% of the entire length) of the time series were used as the training set and the remaining 3 days were reserved for the forecast assessment and validation. In addition to these measured time series, wind speed data at turbine hub height obtained from a numerical weather prediction model was available and this information was used as the exogenous input for artificial neural network training. In particular, the modeled wind speed and direction data over the region occupied by the wind farm were obtained from a NWP model executed with a temporal resolution of 1 h on a computational grid with a 3-km spatial resolution centered on the location of the wind farm. We applied a simple bilinear interpolation (BI) on this coarse-resolution NWP wind speed data to obtain the wind speed at the location of the WT24 wind turbine, which was then subsequently used as an exogenous input for ANN training.
As described in the previous section, we bootstrapped (resampled with replacement) the training data set to generate N = 200 “phantom” (bootstrap) data sets. We used each of these bootstrap data sets to train three-layer ANNs with a variable number of nodes in the hidden layer ranging from 5 to 30 nodes inclusive (so,





3.2. Results
Figure 1 compares the measured wind speed at the hub height for WT24 with the out-of-sample forecasted wind speed obtained from bootstrapping an ensemble of ANNs. The best deterministic forecast for the wind speed based on a statistical combination of the individual forecasts in the super-ensemble [determined in accordance to Equations (10) and (13)] is shown in this figure (dot-dashed line labeled “Best forecast”). A comparison of the best deterministic forecast with the measured wind speed shows that the forecast captures adequately the longer temporal trends in the measured wind speed. In addition, the 95% prediction confidence intervals obtained using the two-stage weighted-averaging method is exhibited in Figure 1 as the dotted lines demarcated using an open circle. Note that the 95% prediction uncertainty range appears to cover most of the observations, providing an observation coverage that is consistent (approximately or better) with the quoted level of confidence in the uncertainty interval. A quantitative assessment of the forecast performance in this case is summarized in Table 1, which summarizes the RMSE and MAE in the wind speed prediction using the bootstrapped neural-network methodology. The performance of this forecast methodology can be compared to that obtained from a simple persistence model forecast which uses the current wind speed to predict the value of the future wind speed.
Next, we consider the forecast performance for the wind power using the bootstrapped neural-network methodology. The forecast for the generated power is more complicated than that for the wind speed owing to

Figure 1. Out-of-sample wind speed forecasting obtained using the bootstrapped neural-network methodology. The 95% confidence interval for the forecast was calculated by using the two-stage weighted-averaging method applied to the ANN members of the super-ensemble.
Table 1. Wind speed forecast assessment of the bootstrapped neural-network methodology.
the fact that the wind power is censored from above. More specifically, wind turbines are designed so that when the wind speed exceeds a certain value (referred to as the rated output wind speed), a limit to the power generation is imposed implying that the power generated is censored from above. To account for this maximum limit in the wind power generation by a wind turbine, the bilinear interpolation of the NWP wind speeds to the location of WT24 were censored (to the rated output wind speed of the turbine) before they were used as the exogenous input for the neural network training. Furthermore, the measured wind power used in the training of the ANNs were already censored from above by the maximum limit for power generation by the turbine. Indeed, for the current example, if the modeled wind speeds exceeded 11.5 m・s?1 (rated output wind speed for WT24), then the generated wind power associated with this range of wind speeds was limited above to 1550 W (rated output power for WT24).
Figure 2 compares the measured power generated by the turbine WT24 with the forecasted wind power obtained using the bootstrapped neural-network methodology. The best deterministic forecast (“Best forecast”) is shown based on a particular statistical combination of the individual forecasts obtained from the various members of the super-ensemble using the two-stage weighted-averaging process. In addition, the 95% con- fidence intervals for the predicted wind power is superimposed on the plot. Table 2 summarizes the values of the RMSE and MAE for power forecasts obtained using the persistence methodology and the bootstrapped neural-network methodology. A comparison of the best deterministic forecast of the power (dash-dotted line) with the measured power shows that the broad features in the variation of the power is captured fairly well. From Table 2, it is seen that this best deterministic forecast gives misfits (either RSME or MAE) that are roughly a factor of three less than those obtained using the simple naïve persistence forecast. The observation coverage for the 95% prediction uncertainty intervals captures the power measurements fairly well, although qualitatively it is judged that this coverage is not as good as for the case of wind speed prediction. This would indicate that there may be sources of uncertainty in the wind power forecasting that have not been accounted for in the bootstrapping process.
4. Summary and Conclusions
In this paper, we proposed a novel bootstrapped artificial neural-network approach for wind speed and generated power forecasting. The approach provides a multi-ANN model super-ensemble that can be used to provide a best deterministic forecasting for these quantities, as well as to provide a quantitative assessment of the related

Figure 2. Out-of-sample wind power forecasting using the bootstrapped neural-network methodology. The 95% confidence intervals for the forecast were calculated by using the two-stage weighted-averaging method applied to the ANN members of the super-ensemble.
Table 2. Wind power forecast assessment of the bootstrapped neural-network methodology.
prediction uncertainty. In this approach, the individual ANNs that comprise the super-ensemble are first trained using a data set of available wind speed and power measurements and wind speed predictions (obtained from a numerical weather prediction model). The training consists of fitting various artificial neural network architectures (model structures) against the observation and exogenous input to determine the optimal statistical weights for each model.
The advantage of this methodology is that the biases in the forecast can be reduced and good predictions (forecasts) can be obtained through a statistical combination of the individual forecasts from the super-ensemble to give the best deterministic forecast. Applications to a wind turbine in northern China show that our proposed method works quite well. Because the method also provides prediction uncertainty bounds in the forecasts, it is anticipated that this approach would be very useful for green electrical system power management. Indeed, with the rapid pace of increases in computational power, it will become easier in the near future for power system managers and energy system traders/analysts to take advantage of the super-ensemble approach, for providing optimal forecasts and quantitative assessments of the uncertainty associated with these forecasts (allowing this information to be used in a more accurate and reliable manner for various applications).
References
- Costa, A., Crspo, A., Navarro, J., Lizano, G., Madsen, H. and Feitosa, E. (2008) A Review on the Young History of the Wind Power Short-Term Prediction. Renewable and Sustainable Energy Reviews, 12, 1725-1744. http://dx.doi.org/10.1016/j.rser.2007.01.015
- Ma, L., Luan, S., Jiang, C., Liu, H. and Zhang, Y. (2009) A Review on the Forecasting of Wind Speed and Generated Power. Renewable and Sustainable Energy Reviews, 13, 915-920. http://dx.doi.org/10.1016/j.rser.2008.02.002
- Foley, A.F., Leahy, P.G., Marvugliaand, A. and McKeogh, E.J. (2012) Current Methods and Advances in Forecasting of Wind Power Generation. Renewable Energy, 37, 1-8. http://dx.doi.org/10.1016/j.renene.2011.05.033
- Box, G.E.P. and Jenkins, G. (1970) Time Series Analysis, Forecasting and Control. Holden-Day, San Francisco.
- Erdem, E. and Shi, J. (2011) ARMA Based Approaches for Forecasting the Tuple of Wind Speed and Direction. Applied Energy, 88, 1405-1414. http://dx.doi.org/10.1016/j.apenergy.2010.10.031
- Engle, R.F. (1982) Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-1007. http://dx.doi.org/10.2307/1912773
- Bollerslev, T. (1986) Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31, 307- 327. http://dx.doi.org/10.1016/0304-4076(86)90063-1
- Liu, H., Erdem, E. and Shi, J. (2011) Comprehensive Evaluation of ARMA-GARCH(-M) Approaches for Modeling the Mean and Volatility of Wind Speed. Applied Energy, 88, 724-732. http://dx.doi.org/10.1016/j.apenergy.2010.09.028
- Martí Perez, I., Nielsen, T.S., Madsen, H., Navarro, J., Roldán, A., Cabezón, D. and Barquero, C.G. (2001) Prediction Models in Complex Terrain. Proceedings of the European Wind Energy Conference, Copenhagen, 2001, 875-878.
- Liu, Y., Warner, T., Liu, Y., Vincent, C., Wu, W., Mahoney, B., Swerdlin, S., Parks, K. and Boehnert, J. (2011) Simultaneous Nested Modeling From the Synoptic Scale to the LES Scale for Wind Energy Applications. Journal of Wind Engineering and Industrial Aerodynamics, 99, 308-319. http://dx.doi.org/10.1016/j.jweia.2011.01.013
- Li, L., Liu, Y., Yang, Y. and Han, S. (2013) Short-Term Wind Speed Forecasting Based on CFD Pre-Calculated Flow Fields. Proceedings of the Chinese Society of Electrical Engineering, 33, 27-32.
- Kariniotakis, G., Stavrakakis, G.S. and Nogaret, E.F. (1996) Wind Power Forecasting Using Advanced Neural Network Models. IEEE Transactions on Energy Conversion, 11, 762-767. http://dx.doi.org/10.1109/60.556376
- Kariniotakis, G. (2003) Forecasting of Wind Parks Production by Dynamic Fuzzy Models with Optimal Generalisation Capacity. Proceedings of the 12th Intelligent System Application to Power Systems 03, ISAP 03/032, Lemnos, September 2003.
- Hornik, K., Stinchcombe, M. and White, H. (1989) Multilayer Feedforward Networks are Universal Approximators, Neural Networks, 2, 359-366. http://dx.doi.org/10.1016/0893-6080(89)90020-8
- Kennedy, J. and Eberhart, R.C. (2001) Swarm Intelligence. Morgan Kaufmann Publishers, San-Francisco.
- Efron, B. and Tibshirani, B. (1993) An Introduction to the Bootstrap. Chapman & Hall/CRC, Boca Raton.
NOTES

1Recall the weights



2Recall that the number of nodes in the input and output layers of the neural network are determined (fixed) by the dimensionality of the input and output vectors, respectively.


