Energy and Power Engineering
Vol.06 No.03(2014), Article ID:44099,9 pages
10.4236/epe.2014.63005
Method for Determination of Optimal Installed Capacity of Renewable Sources of Energy by the Criterion of Minimum Losses of Active Power in Distribution System
P. D. Lezhniuk1, V. A. Komar1, D. S. Sobchuk2
1Department of Electric Power Stations and Systems, Vinnytsia National Technical University, Vinnytsia, Ukraine
2Department of Electric Energy Supply, Lutsk National Technical University, Lutsk, Ukraine
Email: kvo76@mail.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 January 2014; revised 14 February 2014; accepted 21 February 2014
ABSTRACT
New method for determination of optimal placement and value of installed capacity of renewable source of energy (RES) by the criterion of minimum losses of active power, that allows taking into consideration the dependence of RES on natural conditions of region, schedule of energy supply, parameters and configuration of distribution network is suggested in the paper. Results of computations of test scheme confirm the efficiency of the proposed method and its simplicity as compared with the methods considered in literature sources.
Keywords:
Distributed Generation; Renewable Sources of Energy; Minimum Losses of Active Power

1. Introduction
World electric power generation was traditionally developing by the means of centralization of generation system, construction of more powerful power plants and their integration in power complexes. As a result, large geographically extensive power systems were created: the European ENTSO-E, unified power system in Russia, unified power system in Ukraine and others. In the last few years, steady progress in energy sector of national economy restructuring greatly changed general concept of power branch development, it concerns the introduction of new ideology, namely introduction of distributed power generation. Distribution Generation System (DGS) is defined as sources of electrical energy, connected directly with distribution system or connected to such network on the side of consumers. Wide spread of DG is connected with the introduction of high-efficient gas-turbine and steam-turbine plants [1] and development of renewable sources of energy. Among them the most widespread are wind electric plants (WEP) and photovoltaic systems (PVS).
Introduction of DG in electric networks, especially constructed on the base of renewable sources of energy (RSE), besides reduction of ecological impact l on the environment and solution of many problems connected with harmful emissions as a result of energy generation production, allows, first, sufficiently increasing the efficiency of resources utilization, and in future reducing the cost of electric energy, unload transmission lines and distribution systems.
Installation of DG sources in distributive electric networks near consumption centers changes direction of power flows. It is necessary to distinguish three situations concerning load nodes and DG [2] :
Power of each node in electric network is greater or equals the power of DG sources, connected to these nodes.
2. In electric network there exists one node, where the power of DG is greater than the power of this node load, but total power of DG sources of this network on the whole is less, than its total load.
3. In electric network there exists minimum one node, where DG power exceeds the power of this node load and total power of DG sources of this network on the whole is greater than its total load.
In the first case DG sources placed in electric network will influence the reduction of power losses in distribution networks. In the second case DG sources can permanently increase power losses in some lines of distribution network, but generally, total power losses are decreased. In the third case, total power losses of the distribution network will be higher than the prior installation of DG sources. Also different DG sources operate with different cosφ and their output reactive power can vary from insignificant generation (steam-turbine plants) to significant consumption (FES with asynchronous generators), that also negatively influences the magnitude of power losses in electric networks [3] .
2. Analysis of the Research
Intensive introduction of distributed generation (DG) created a number of problems, one of which is the selection of the location for the connection to the network and their installed capacity. The solution of this problem enables to obtain necessary effect as a result of the introduction of dispersed generation source?reduction of power losses and enhancement of power quality.
The analysis of the existing approaches allows making a conclusion regarding the directions of the research. The existing methods are based on various approaches: analytical methods [4] [5] ; mixed integer programming [6] ; heuristic approach [7] ; genetic algorithms [8] , loss sensitivity factor method [9] . And it is only a part of research, performed in this direction. Each of the methods has its advantages, enabling to take into account certain peculiarities of distributed generation (DG) and renewable energy sources (RES). But none of the methods allows taking into account the dependence of renewable source of energy generation schedule on natural conditions. This factor is very important, especially for solving the problem of the selection of the installed capacity.
3. Characteristics of Renewable Sources of Energy
The comparison of the schedules of power consumption and generation, by such renewable sources of energy as photovoltaic (PV) and wind-electric plants (WEP) allows speaking about their low stability regarding the support of power balance (see Figures 1 and 2). In the problem of power balance support the capacities of PV and WEP can be referred to conventionally controlled sources. That is, theoretically it is possible to change generation, within the limits, dependent on natural conditions but, in this case their efficiency will be considerably reduced. That is why, it is expedient to develop such a method that would allow taking into consideration such characteristic feature of renewable sources of energy (RSE) in the problem of selection of their installed capacity.
To take into account the random component of generation schedules relatively the schedules of power consumption is possible by means of the analysis of the most probable generation values and the most probable values of consumption at the definite periods of the day. For each hour of the day the following dependences are constructed:
Figure 1. Seasonal change of daily schedule of PVS operation.
Figure 2. Change character of average values of PVP generation, determined by daily schedules during the year.
Depending on the number of corresponding levels occurrences (generation, consumption) their probabilities can be determined:
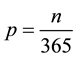 , (1)
, (1)
where ?is the number of levels occurrences (generation, consumption)during a year.
?is the number of levels occurrences (generation, consumption)during a year.
Having all the probabilities, the stability factor can be evaluated; this factor will characterize the probability of electric energy supply, generated by renewable source of energy, of the consumers, connected to corresponding feeder of distribution system. Instability factor can be determined by the expression:
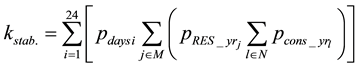 , (2)
, (2)
where ―is the probability of occurrence of the daily schedule stage
―is the probability of occurrence of the daily schedule stage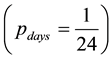 ;
;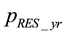 ―is the pro-
―is the pro-
bability of the occurrence of the generation stage during a year, is determined by the expression (1);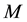 ―is the set of non-zero stages;
―is the set of non-zero stages;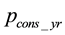 ―is the probability of the occurrence of the consumption stage during a year, is determined by the expression (1);
―is the probability of the occurrence of the consumption stage during a year, is determined by the expression (1);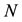 ―is the set of consumption stages which are below the generation level of the corresponding period of the day (see Figure 3).
―is the set of consumption stages which are below the generation level of the corresponding period of the day (see Figure 3).
Stability factor enables to evaluate the possibilities of the source to cover the necessary consumption of electric energy. It depends on the power of electric energy source. For the accounting of energy supply it is suggested to introduce the coefficient, that is determined by the ratio of the expectation of annual consumption
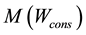 to expectation of RES annual generation
to expectation of RES annual generation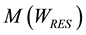 :
:
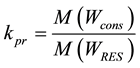 . (3)
. (3)
Necessary expectations can be determined analyzing annual graphs by the duration (see Figure 4).
The suggested coefficients allow characterizing the source of electric energy relatively natural conditions and schedule of the consumption to be covered.
4. Method of Determination of RES Installed Capacity
The introduction of dispersed generation sources in the distribution systems has created a number of problems, namely, they must be considered not as main-radial but as networks with double sided supply or local electrical system (LES). That is why, to evaluate the necessary installed capacity of DG it is expedient to carry out the analysis of power flows distribution in LES.
For this purpose we consider the problem of determination of currents that provide minimum losses of active power in LES. In general case, if technical constraints with the current of generating nodes are missing, the objective function can be formulated in the following way:
Minimize
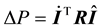 (4)
(4)
if
Figure 3. Probability levels of generation 1 and consumption 2 of the definite period of time during a year.
Figure 4. Annual schedules of generation 1 and consumption by duration.

where

It should be noted, that the solution of the formulated optimization problem (4) on condition (5) allows determining not only optimal currents in the branches of the network but also establish optimal, from a viewpoint of active power losses minimization, supply sources loads If active, reactive or full load of any supply source is fixed, then in matrix M' the row, corresponding to this node, must be present and the current must be included in the vector of nodal currents with corresponding sign.
For determining minimum losses of active power and values of optimal currents in corresponding branches, we will make use of Lagrangian multiplier method. Lagrangian function for (4) taking into consideration the constraint Equations (5)
where
From the condition of zero equality of partial derivatives W by variables, being optimized and Lagrangian multipliers we obtain the following system of Equations:
where optimal currents in the branches and Lagrangian multipliers:
where symbol


Having divided the expression in brackets into blocks, as it is shown with heavy lines and applied Frobenius formula:
where




and

After simple transformations we obtain the solution of the problem of optimal currents determination in the branches:

where

Vectors of active and reactive components of generating nodes optimal currents
where M''―is the matrix, lines of which are lines of the connections matrix, corresponding to generating nodes.
Proceeding from the solution of the problem (4), we can make a conclusion, that minimum losses of active power in LES for the case, when constrains are not imposed on nodal currents, occur when active and reactive components of currents are distributed in it depending on resistances, i.e., according to r-equivalent circuit of LES. This result can be extended to power transfers.
Using the assumption that there are no transfers of reactive power and reactive components of equivalent circuit of network elements, we obtain the dependence in matrix form for active power transfers in the branches of the network:

where


From the system of Equations, obtained by differentiation with variables from (7), Lagrangian undetermined multipliers can be determined in the form:

where

After substitution of (8) into (7) we obtain

In (9) the expression


Rewrite (9) in the form

Similar results can be obtained taking into consideration the transfers of reactive power, that is why the Equation (10) will be valid for full power.
Using (10) we can develop the method of RES installed capacity determination by the criterion of minimum losses of active power.
5. Algorithm of the Method
The information to be used for the start of the computation is statistical data (minimum for the previous year) and the forecast, regarding natural conditions (solar radiation, wind flows); load curves of feeder’s nodes, equivalent circuit and parameters of feeder’s elements (see Figure 5).
6. The Results of Research
For validation of the performance of the developed method the feeder was considered, its circuit is shown in Figure 6.
Let us consider, as possible by technical conditions, nodes for RES 7, 10 and 20 connection. For the selection of the best, by energy losses criterion, we will determine current distribution coefficients for each of the variants.
Figure 5. Algorithm of the method.
Figure 6. Fragment of distribution network.
Values of

Table 1. Analysis of the vectors of current distribution coefficients.
Figure 7. Computation results for the case of PVP placement in node 20.
Figure 8. Computation results for the case of PVS placement in node 10.
PVS is installed in node 10 than in node 20.
For comparison the computation of active power losses during the year was carried out by means of exhaustive search of different powers of PVP for the investigated schedule of generation and consumption.
Graphic interpretation of the results is shown in Figure 7 (for node 20) and Figure 8 (for node 10)
In Figures 7-9 curve 1―change of active power losses during a year, obtained by means of exhaustive search
Figure 9. Computation results for the case of PVS placement in node 7.
of the installed capacities of PVS; curve 2―change of active power loss during a year, obtained as a result of exhaustive search of installed capacities s of PVS on condition that the installed capacity of the source is selected as a result of analysis of the most probable stage of power consumption; curve 3―change of active power loss during a year, obtained as a result of exhaustive search of the installed capacities of PVS on condition, that the operation mode of the plant is stipulated not only by natural conditions but also by the schedule of power consumption.
7. Conclusions
The suggested method of determination of optimal installed capacity of RES allows taking into consideration the dependence of their operation schedule on natural conditions, point of connection to distribution grid and loading curve. The algorithm of the method is easily formalized and realized in the form of programming product, which distinguishes it from the methods considered in the survey.
Calculations performed, prove the validity of the method both regarding the problem of determination of the point of RES connection and regarding the determination of the optimal power of the source by the criterion of minimum losses of electric energy.
References
- Bieliaiev, L.S., Lahariev, A.V. and Posiekalin, V.V. (2004) Power Engineering of XXI Century: Conditions of Development, Technologies, Forecasts. Science, Novosibirsk, 386.
- Ackerman, T., Knyazkin, V. (2000) Interaction between Distributed Generation and the Distribution Network. Transmission and Distribution Conference and Exhibition: Asia Pacific IEEE/PES, 1357-1362.
- Gonzalex-Longatt, F. (2007) Impact of Distributed Generation over Power Losses on Distribution System. 9th International EPQU Conference, Barcelona.
- Acharya, N., Mahat, P. and Mithulananthan, N. (2006) An Analytical Approach for DG Allocation in Primary Distribution Network. International Journal of Electrical Power & Energy Systems, 28, 669-678. http://dx.doi.org/10.1016/j.ijepes.2006.02.013
- Hung, D.Q., Mithulananthan, N. and Bansal, R.C. (2010) Analytical Expressions for DG Allocation in Primary Distribution Networks. IEEE Transactions on Energy Conversion, 25, 814-820. http://dx.doi.org/10.1109/TEC.2010.2044414
- Chang, R.W., Mithulananthan, N. and Saha, T.K. (2011) Novel Mixed-Integer Method to Optimize Distributed Generation Mix in Primary Distribution Systems. 2011 21st Australasian Universities Power Engineering Conference (AUPEC), Brisbane, 25-28 September 2011, 1-6.
- Abu-Mouti, F.S. and El-Hawary, M.E. (2011) Heuristic Curve-Fitted Technique for Distributed Generation Optimisation in Radial Distribution Feeder Systems. IET Generation, Transmission & Distribution, 5, 172-180. http://dx.doi.org/10.1049/iet-gtd.2009.0739
- Singh, D. and Verma, K.S. (2009) Multiobjective Optimization for DG Planning with Load Models. IEEE Transactions on Power Systems, 24, 427-436. http://dx.doi.org/10.1109/TPWRS.2008.2009483
- Griffin, T., et al. (2000) Placement of Dispersed Generation Systems for Reduced Losses. Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Hawaii, 4-7 January 2000.

















