Energy and Power Engineering
Vol.6 No.1(2014), Article ID:42283,7 pages DOI:10.4236/epe.2014.61002
Transient Stability Improvement of Power System Using Non-Linear Controllers
Electrical Engineering Department, NIT Jamshedpur, Jamshedpur, India
Email: rchy72@gmail.com, aksnitjsr@gmail.com
Received November 20, 2013; revised December 10, 2013; accepted December 17, 2013
ABSTRACT
This paper presents the design of a non-linear controller to prevent an electric power system losing synchronism after a large sudden fault and to achieve good post fault voltage level. By Direct Feedback Linearization (DFL) technique robust non-linear excitation controller is designed which will achieve stability enhancement and voltage regulation of power system. By utilizing this technique, there is a possibility of selecting various control loops for a particular application problem. This method plays an important role in control system and power system engineering problem where all relevant variables cannot be directly measured. Simulated results carried out on a single machine infinite bus power system model which shows the enhancement of transient stability regardless of the fault and changes in network parameters.
Keywords:Single Machine Infinite Bus (SMIB); Direct Feedback Linearization (DFL); Fuzzy Logic Controller (FLC); Sliding Mode Control (SMC)
1. Introduction
In this paper, the problem of transient stability and voltage regulation after a sudden disturbance in power system is considered. The problem of transient stability is frequently considered which is concerned with the maintenance of synchronism between generators following a severe disturbance. Due to large disturbance, changes in angular differences may be so large as to cause the machine to fall out of step. This type of instability is known as transient instability and is a fast phenomenon usually occurring within a second.
The system stability after fault depends not only on the system itself but also on the type of fault, location of fault, rapidity of clearing the fault and method of clearing. The controller for nonlinear system has been developed significantly during the last few decades due to its wide applicability to many practical systems such as aerospace vehicles and other nonlinear problems. Non-linear controller can handle the non-linearities in large range operation, as the controller is designed for handling the nonlinear system directly.
Gordon and D. J. Hill [1] presented the direct feedback linearization (DFL) technique as a simple and flexible nonlinear control method to design robust nonlinear excitation controllers for stability enhancement and voltage regulation of power system. A new nonlinear control scheme was proposed by Mou Chen and Wen-Hua Chen [2] for a class of nonlinear systems subjected to unknown disturbances where the Sliding Mode Control (SMC) scheme is integrated with disturbance observers.
The application of DFL to power system stability control has received a great deal of attention. By using DFL technique, various non-linear controllers [1] for a generator excitation can be developed. Y. Wang, G. Guo, D. J. Hill [3] applied DFL to transfer a non-linear multi-machine power system problem to a linear one as well as robust decentralized control is also obtained. Solving a set of Algebraic Riccati Equations (ARE) gives controller parameters which guarantee the overall stability of the excitation system.
The structure of this paper is as follows. Section 2 presents the dynamical model of power system. Wherein the system has been discussed for which the simulation has been carried out later. Section 3 describes the controller design techniques, here direct feedback linearization has been discussed and in the subsections the modeling of the system and the fuzzy logic controller was presented. The simulation results are presented in Section 4 of the paper. The simulation has been carried out for a particular case of initial angle and mechanical power. The paper has been concluded in Section 5 with some focus on the future work.
2. Dynamical Model of Power System
A Single Machine Infinite Bus (SMIB) power system is considered in this paper as a SMIB system qualitatively exhibit important aspects of the behavior of a multi-machine system and is relatively simple to study. It is extremely useful in describing the general concept of power system stabilizer, the influence of various factors upon stability and alternative controller concepts. In power system dynamics, the most important component is the synchronous generator with its associated excitation control [4]. Although the actual dynamic response of a synchronous generator in a practical power system when a fault occurs is very complicated including many nonlinearities such as the magnetic saturation, the classical third order dynamic generator model is commonly used for designing the excitation controller.
The single machine infinite bus model for power system is shown in Figure 1. The classical third order dynamical model of a SMIB power system can be written below:
Mechanical equation:
 (2.1)
(2.1)
 (2.2)
(2.2)
Generator electrical dynamics:
 (2.3)
(2.3)
Electrical equations:
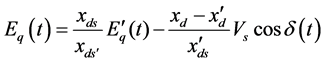 (2.4)
(2.4)
 (2.5)
(2.5)

Figure 1. Schematic model of SMIB system.
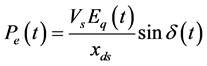 (2.6)
(2.6)
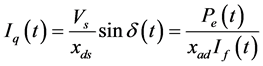 (2.7)
(2.7)
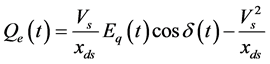 (2.8)
(2.8)
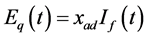 (2.9)
(2.9)
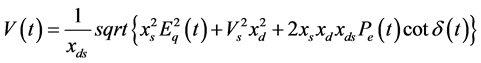 (2.10)
(2.10)
For the equations 2.1 to 2.10, the parameter values are provided in the Appendix appearing at the last.
The fault considered in this paper is a symmetrical three-phase fault, permanent type.
The fault sequence is described as:
Stage 1: The system is in a pre-fault steady-state.
Stage 2: A fault occurs at t = 0.1 sec. The fault location is indexed by a positive constant λ which is fraction of line to the left of the fault. In this case λ is equal to 0.2.
Stage 3: The fault is removed by opening the breakers of the faulted line at t = 0.25 sec.
Stage 4: The system is in a post-fault state.
3. Controller Design Technique
During the last three decades, various control strategies have been proposed on the basis of linearisation techniques for linearizing nonlinear power system model [5]. These can be broadly classified into linear and nonlinear control strategies, such as Standard Linearisation Techniques (SLT) based on Taylor’s series approximation, Direct Feedback Linearisation (DFL) and linearisation of nonlinear model based on Differential Geometric Technique. The modeling difficulties in these techniques are presented in [5]. Also, the design of state feedback control law based on these techniques requires the measurement of all the states. Some-times the measurements may not be feasible or economical. To avoid measuring the state variables a suitable observer is required to estimate the states so as to enable to generate state feedback control signal. The designed state observer [14] for uncertain nonlinear systems must possess capabilities such as reducing noise, inherent robustness for parametric uncertainties etc. The popular techniques for designing the observers are 1) Luenberger observer 2) Kalman Filter and 3) Sliding Mode Strategy (SMS).
FLC has emerged as one of the most active and effective approaches to control the complex system such as power systems [6-8]. Combining the optimization tool like Genetic Algorithm (GA) with GLC for tuning increases the intelligence of the controller and also fast tuning is achieved [12,13]. This is due to the fact that the system knowledge and dynamic behavior are qualitative and uncertain, so the fuzzy set theory appears to provide a suitable representation of such knowledge. Usually, the qualitative knowledge is represented by fuzzy sets, and then, by using compositional rule of inference and approximate reasoning, a fuzzy control law can be constructed.
The paper [2] proposed a Sliding Mode Observer (SMO) based Fuzzy Logic Controller designated as Observer based Fuzzy Logic Controller (OFLC), which integrates the advantages of sliding mode and fuzzy logic concepts. In this paper, for the FLCs design, generator speed deviation and acceleration are taken as inputs. It has been treated that, the variations in the speed and acceleration of each machine of a Multi Machine Power System (MMPS) is a local problem, and hence, an individual controller is designed to each generator, which initiates a local control action.
3.1. Mathematical Analysis of Controller
The non-linear controller considered here is a dynamic DFL compensator through the excitation loop to cancel the non-linearities and interactions among generators and a robust feedback controller to guarantee the asymptotes stability of the DFL compensation system. It considers the effects of dynamic output feedback and plant parametric uncertainties. The non-linear controller can guarantee the stability of the non-linear power systems within a whole operating region for all admissible parameters.
The DFL technique [8] is very useful method for power system non-linear controller design. By employing a non-linear feedback compensating law, a non-linear system can be directly transformed to a system whose closed loop dynamics are linear over a very wide range. To design a non-linear controller for the power system, since
 is physically un-measurable, we eliminate
is physically un-measurable, we eliminate 
by differentiating Equation (6) and using (1) to (6)
Equation (6) is 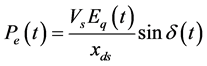
Differentiating the above equation with respect to time and doing the required assumptions, we get the following three equations:

We have 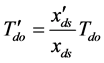
where,
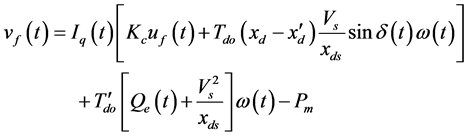
The model (1) to (3) can now be linearized and the linearized model is obtained as:
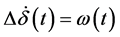 (3.1)
(3.1)
 (3.2)
(3.2)
 (3.3)
(3.3)
where 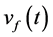 is the new input.
is the new input.
After linearization, we can employ linear control theory, such as LQ-optimal control theory, to design a feedback law given as

Some computer simulations will be provided on a single-machine infinite-bus (SMIB) power system. The fault considered in this paper is a symmetrical three-phase short circuit fault, which occurs on the infinite bus and is removed after a certain time.
3.2. Fuzzy Logic Controllers
Despite the potential of modern control techniques with different structures, power system utilities still prefer the conventional lead-lag controller design. The gain settings of these stabilizers are determined based on the linearized model of the power system around a nominal operating point. Since power system are highly non-linear and the operating conditions can vary over a wide range, conventional power systems performance is degraded when the operating point changes from one to another because of fixed parameters of the stabilizers. Also conventional techniques are time consuming as they are iterative and require complex computation procedures and show convergence.
Recently metaheuristic optimization technique like GA, Tabu Search, simulated annealing, Bacteria foraging, PSO [9-11] have been applied for PSS parameter optimization. In this paper PSO algorithm has been implemented to calculate the optimum value of PSS parameters. PSO is a population based stochastic optimization technique inspired by social behaviour of bird flocking or fish schooling [11]. PSO shares many similarities with GA like initialization of population of random solution and search for the optimal solution by updating generations.
Fuzzy logic control is a method based on fuzzy set theory, in which the fuzzy logic variables can be of any value between 0 and 1 instead of just true or false. When the variables are selected, the decision will be made through specific fuzzy logic function. Although FLC have been successfully applied in many complex industrial processes, they experience a deficiency in knowledge acquisition and rely to a great extent on empirical and heuristic knowledge which in many cases can’t be obtained easily. Moreover, there is no generalized method for the formulation of fuzzy control strategies, and design relies on repeatedly modification of control rules to obtain satisfactory performance. FLC controls have been demonstrating their feasibility in the field use. Expert’s knowledge can be incorporated into fuzzy rules. Design of FLC’s are generally used to determine the input and output variables, parameters of membership functions, fuzzy rules and to improve performance of FLC.
Figure 2 shows the design methodology for implementation of fuzzy logic controller. It consists of two parts namely design and control. The design part carries out defining the system, defining the fuzzy universe of discourse, defining control rules and finally simulating it. The control part consists of fuzzy controller and implementing it on the process.
Figure 3 shows the Matlab implementation of fuzzy logic controller for a linearized model. For implementing it a rule base consisting of 25 rules has been designed.
Table 1 shows the rule base for a 5 × 5 membership function, where ∆ɷ and ∆ὼ are the inputs to the fuzzy logic controller.

Figure 2. Fuzzy design methodology.
Table 1. Rule base with five membership function.
4. Simulation Results
Through computer simulation, results for different cases of power angle and terminal voltage have been shown. The controllers employed in the simulations are DFL-LQ controller, voltage controller and co-ordinated controller.
DFL-LQ controller
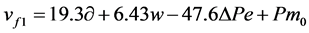 (4.1)
(4.1)
Voltage controller
Voltage regulation is an important issue particularly in the post-transient period. The voltage controller can be given mathematically as:

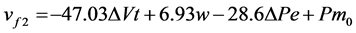 (4.2)
(4.2)
To combine the advantages of DFL-LQ controller and voltage controller, a co-ordinated controller is designed with a switching scheme. The switching scheme, which is taken here is as follows:
Step 1: when fault occurs at t = t0, the DFL non-linear controller uf with 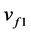 is employed to maintain transient stability.
is employed to maintain transient stability.
Step 2: At the switching time, the control law switches to voltage controller uf with 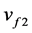 to maintain desired post-fault voltage level.
to maintain desired post-fault voltage level.
The switching time ts should be reasonably chosen within the post-transient period, which requires that the fault sequence must be known as a prior. Further the exact switching time has to be determined by trial in simulation.
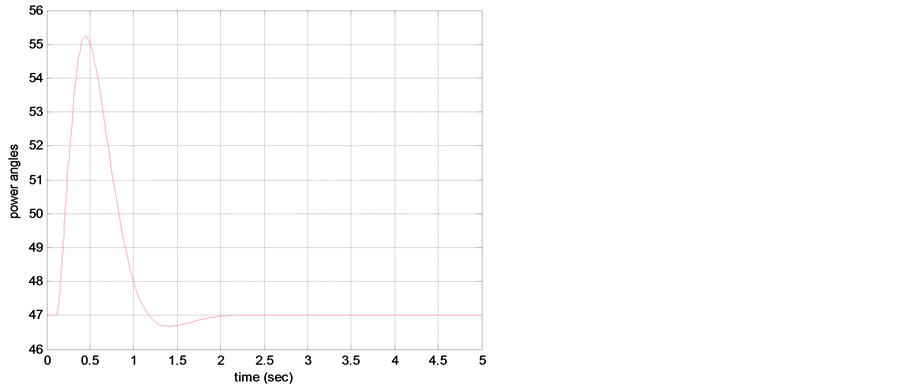
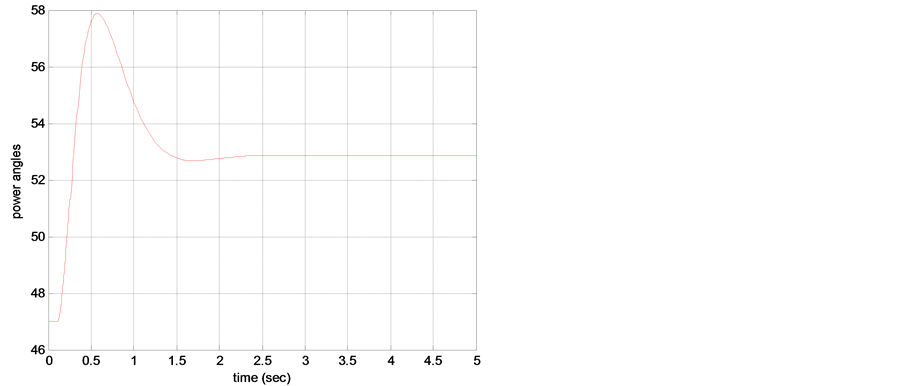
Figures 4(a) and (b) show the power angle and terminal voltage response for DFL-LQ controller (with initial angle 47 and Mechanical power, Pm0 = 0.45). Figures 5(a) and (b) show the power angle and terminal voltage response for voltage regulator (with initial angle 47 and Pm0 = 0.45). The simulation results for co-ordinated controllers are shown in Figures 6(a) and (b) for the same initial angle and mechanical power as taken above.
It is observed that using only DFL-LQ optimal controller or a DFL voltage regulator, one cannot achieve both good transient response and good post-fault perfor-
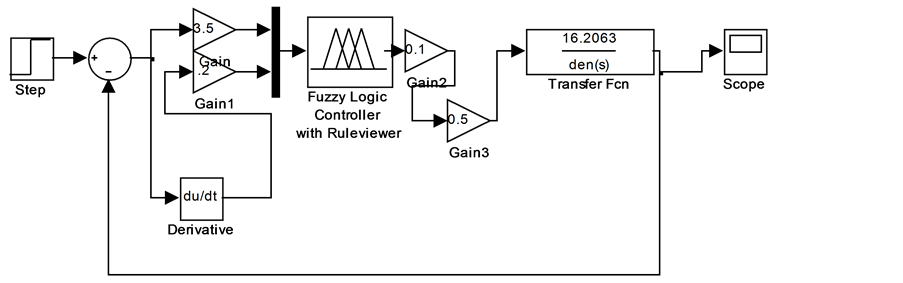
Figure 3. MATLAB model for fuzzy logic controller.
 (a)
(a)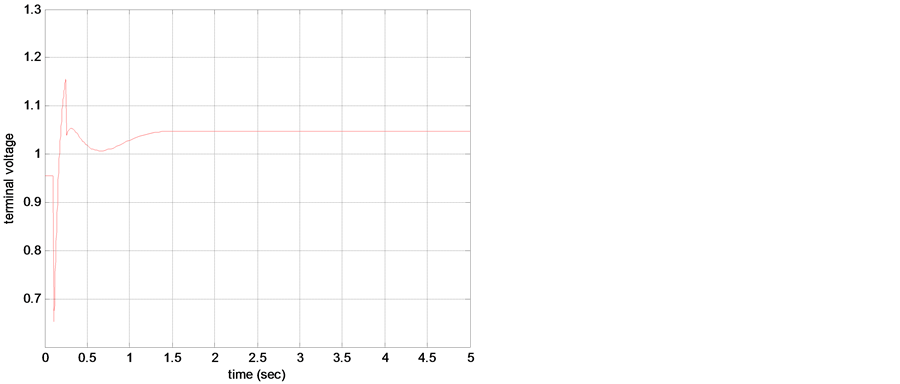 (b)
(b)
Figure 4. (a) Power angle response for DFL-LQ, (b) Terminal voltage response for DFL-LQ.
 (a)
(a)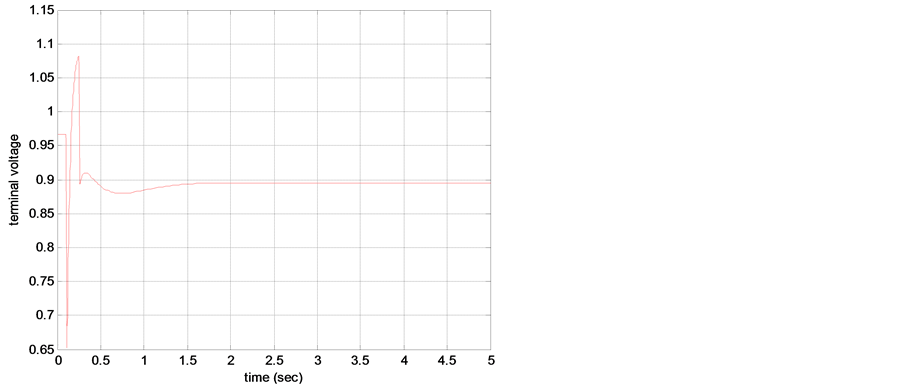 (b)
(b)
Figure 5. (a) Power angle response for voltage regulator, (b) Terminal voltage response for voltage regulator.
mance. To overcome these problems a typical switching scheme is selected. The switching time should be reasonably chosen within the post-transient period, which requires that the fault sequence must be known as a prior. Further the exact switching time has to be determined by trial in simulation.
 (a)
(a) (b)
(b)
Figure 6. (a) Power angle response for co-ordinated controller, (b) Terminal voltage response for co-ordinated controller.
5. Conclusion
Large scale power systems are the one where a number of generating units are connected together by a transmission line. As physical limitation on the system structure makes information transfer among subsystems unfeasible, so decentralized controllers might be used in large scale power system control. Transient stability is a major requirement in power system operation which is concerned with the maintenance of synchronism between generators following a severe disturbance. Enhancement of transient stability can be implemented through the excitation control loop where field voltage and current are supplied to generator and through the steam valve control loop where mechanical power is supplied.
The switching controller with switching time stabilizes the system but it does not always do so as switching time is varied. So, it can be concluded that the strategy by simply switching between different control actions is not reliable due to non-existence of universal switching time. So to overcome the above demerits global control strategy or designing a fuzzy based controller is proposed which may achieve transient stability enhancement and voltage regulation simultaneously.
Acknowledgements
We would sincerely like to thank Professor Kanti B. Datta, Retired Professor, IIT Kharagpur, for his kindcooperation as without his help it would not have been possible to compile this paper.
REFERENCES
- M. Gordon and D. J. Hill, “Flexible Non-Linear Voltage Control Design for Power System,” 16th IEEE International Conference on Control Applications, 2007, pp. 1097-1102.
- M. Chen and W.-H. Chen, “Sliding Mode Control for a Class of Uncertain Nonlinear System Based on Disturbance Observer,” International Journal of Adaptive Control and Signal Processing, Vol. 24, No. 1, 2010, pp. 51- 64.
- Y. Wang, G. Guo and D. J. Hill, “Robust Decentralized Nonlinear Controller Design for Multi-Machine Power System,” Automatica, Vol. 33, No. 9, 1997, pp. 1725- 1733. http://dx.doi.org/10.1016/S0005-1098(97)00091-5
- C.-C. Peng and C.-L. Chen, “Dynamic Controller Design for a Class of Nonlinear Uncertain Systems Subjected to Time-Varying Disturbance,” Nonlinear Dynamics, Vol. 57, No. 3, 2009, pp. 411-423. http://dx.doi.org/10.1007/s11071-008-9451-2
- Y. Cao, L. Jiang, S. Cheng, O. Malik and G. Hope, “A Nonlinear Variable Structure Stabilizer for Power System Stability,” IEEE Transactions on Energy Conversion, Vol. 9, No. 3, 1994, pp. 489-495. http://dx.doi.org/10.1109/60.326467
- Y. Wang, D. J. Hill, R. Middleton and L. Gao, “Transient Stability Enhancement and Voltage Regulation of Power Systems,” IEEE Transactions on Power Systems, Vol. 8, No. 2, 1993, pp. 620-627. http://dx.doi.org/10.1109/59.260819
- M. A. Abido, “Pole Placement Technique for PSS and TCSC Based Stabilizer Design Using Simulated Annealing,” International Journal of Electrical Power & Energy Systems, Vol. 22, No. 8, 2000, pp. 543-554. http://dx.doi.org/10.1016/S0142-0615(00)00027-2
- Y. Guo, D. J. Hill and Y. Wang, “Global Transient Stability and Voltage Regulation for Power System,” IEEE Transactions on Power Systems, Vol. 16, No. 4, 2001, pp. 678-688. http://dx.doi.org/10.1016/j.epsr.2006.11.006
- M. A. Abido, “Robust Design of Multi-Machine PSS Using Simulated Annealing,” IEEE Transactions on Energy Conversion, Vol. 15, No. 3, 2003, pp. 297-304.
- S. Mishra and M. Tripathy, “Multi-Machine PSS Design by Rule Based Bacteria Foraging,” Electric Power System Research, Vol. 77, No. 12, 2007, pp. 1595-1607. http://dx.doi.org/10.1016/j.epsr.2006.11.006
- B. Zhao and Y. Cao, “A Multiagent Based PSO Approach for Optimal Reactive Power Dispatch,” IEEE Transactions on Power system, Vol. 20, No. 2, 2005, pp. 1070- 1078. http://dx.doi.org/10.1109/TPWRS.2005.846064
- M. A. Abido and Y. L. Abdel-Magid, “Tuning of Fuzzy PSS Using GA,” 4th IEEE International Conference on Evolutionary Computation ICEC, 1997, pp. 595-599.
- M. A. Abido and Y. L. Abdel-Magid, “Hybridizing RuleBased PSS with GA,” IEEE Transactions on Power System, Vol. 14, No. 2, 1999, pp. 600-607. http://dx.doi.org/10.1109/59.761886
- M. A. Mahmud, M. J. Hossani and H. R. Pota, “NonLinear Observer Design for Interconnected Power Systems,” Australian Control Conference, Melbourne, 10-11 November 2011, pp. 161-166.
Appendix
The parameters of SMIB power system are as follows:
xd= 1.863, xd’ = 0.257, xT = 0.127
 = 6.9, xL = 0.4853, H = 4, D = 5Kc = 1, xad = 1.712, w0 = 314.159 The physical limit of excitation voltage is taken as −3 ≤ Kc uf ≤ 6 The operating point of the power system used insimulation is:
= 6.9, xL = 0.4853, H = 4, D = 5Kc = 1, xad = 1.712, w0 = 314.159 The physical limit of excitation voltage is taken as −3 ≤ Kc uf ≤ 6 The operating point of the power system used insimulation is:
δ0 = 47, Pm0 = 0.45 p.u, Vt0 = 1.0 p.u.


