Energy and Power Engineering
Vol. 4 No. 2 (2012) , Article ID: 18018 , 8 pages DOI:10.4236/epe.2012.42009
A Study on the Functional Reliability of Gravity Dam
1School of Civil and Hydraulic Engineering, Dalian University of Technology, Dalian, China
2State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, China
Email: xuqiang528826@163.com, {*eerd001, lijing}@dlut.edu.cn
Received December 24, 2011; revised January 20, 2012; accepted February 8, 2012
Keywords: Concrete Gravity Dam; Random Load; Functional Reliability; Pseudo Excitation Method
ABSTRACT
The research objective is to design and construct a method for functional reliability analysis of concrete gravity dam. Firstly, the pseudo excitation method was utilized to analyze to calculate the probabilistic characteristics of concrete gravity dam excited by random seismic loading. Meanwhile, the response surface method based on weighted regression was associated to that method to analyze functional reliability of concrete gravity dam. Eventually, a test example was given to verify and analyze the convergence and stability of this method.
1. Introduction
The basic purpose of structural reliability analysis is to obtain the probabilistic responses of structural systems with uncertain design parameters, such as loadings, material parameters (strength, elastic modulus, Poisson’s ratio, etc.), and shape dimensions. Among the methods available for these problems, the response surface method (RSM) is a powerful tool [1]. The theory and methods of RSM have been developed significantly during the last twenty years and have been documented in an increasing number of publications. Although, from a theoretical point of view, the field has reached a stage where the developed methodologies are becoming widespread, RSM used to analyze large structures is still a complex and difficult task. In order to solve this problem, a rigorous series of tests has to be carried out. Linda and Ping (1999) [2] constructed confidence intervals about the difference in mean responses at the stationary point and alternate points based on the proposed delta method and F-projection method and compared coverage probabilities and interval widths. Zheng and Das (2000) [3] proposed an improved response surface method and applied that to the reliability analysis of a stiffened plate structure. Guan and Melchers (2001) [4] evaluated the effect of response surface parameter variation on structural reliability. Byeng and Kyung (2004) [5] proposed the hybrid mean value (HMV) method for highly efficient and stable RBDO by evaluating the probabilistic constraint effectively. Gupta and Manohar (2004) [6] used the response surface method to study the extremes of Von Mises stress in nonlinear structures under Gaussian excitations. Herbert and Armando (2004) [7] compared RSM and the artificial neural network (ANN) techniques. Irfan and Chris (2005) [8] proposed a new response surface called ADAPRES, in which a weighted regression method was applied in place of normal regression. Wong et al. (2005) [9] proposed an adaptive design approach to overcome the problem, which was that the solution of the reliability analysis initially diverged when the loading was applied in sequence in the NLFE analysis, and made several suggestions to improve the robustness of RSM. Jiang et al. (2006) [10] improved the method to fit the indeterminate coefficients of response surface. Jin Weilian and Yuan (2007) [11] presented a response surface method based on least squares support vector machines (LS-SLM) aiming at the reliability analysis problems with implicit performance function. Chebbah (2007) [12] dealt with the optimization of tube hydro forming parameters in order to reduce defects which might occur at the end of forming process such as necking and wrinkling by RSM. Jin et al. (2008) [13] presented a new artificial neural net work-(ANN) based response surface method in conjunction with the uniform design method for predicting failure probability of structures. Henri and Siu (2008) [14] described the use of higher order polynomials in order to approximate the true limit state more accurately in contrast to recently proposed algorithms which focused on the positions of sample points to improve the accuracy of the quadratic the stochastic response surface method (SRSM). TongZou et al. (2008) [15] presented an accurate and efficient Monte Carlo simulation method for limit-statebased reliability analysis at both component and system levels, using a response surface approximation of the failure indicator function. Xuan et al. (2009) [16] proposed an adaptive construction of the numerical design, in which the response surface was fitted by the weighted regression technique, which allowed the fitting points to be weighted according to their distance from the true failure surface and their distance from the estimated design point.
To date, however, most reliability methods such as the first order reliability method (FORM) [17], the secondorder reliability method (SORM) [18,19], the weighted regression method (WRM) [20,21], and the space reduced weighted regression method (SRWRM) [22] cannot be used to analyze large structures. These traditional reliability methods have two aspects of deficiencies. On the one hand, limited state function is usually implicit when we use a finite element method (FEM) to analyze structure. It leads to the difficulty in obtaining implicit limited state function for basic random variables. On the other hand, in order to overcome the above defects, some reliability methods use polynomial response surface function to fit implicit limited state function, but the number of basic random variables is very large when analyzing large structures. And these reliability methods need more experimental points to confirm the indeterminate coefficients of these basic random variables. It follows that, during the process, the calculation efficiency and the storage efficiency of these methods are very low. Even in some large structures, it is impossible to obtain enough experimental points. Therefore, most of reliability methods only can be used to analyze small structures.
It has now been widely recognized that the most reasonable method for dealing with such multiple excitation problem is the random vibration approach. Among a great deal of research activities, the reach work by Kiureghian [23] and Ernesto [24] are representative. They all developed their research about the seismic analysis of longspan structures based on random vibration approach. Nevertheless, when solving the high degree random differenttial equations, they all faced unacceptable computational efforts. Compared to these algorithms, Lin [25] proposed a pseudo-excitation method, which was an accurate and highly efficient algorithm series for linear structural stationary random response analysis, to deal with dynamic response of structures subject to random seismic excitation. In this method, the determination of random response of a linear structure was converted to the determination of response of the structure under a series of harmonic loads. By using this algorithm series, the aforementioned difficulties in the stationary random response computations of long-span structures were satisfactorily resolved. Based on this algorithm, Lin [26] et al. analyzed nonstationary random responses of linear structures subjected to evolutionary random excitation. The analytic thought was that the random excitation was first transformed into a pseudo excitation to generate deterministic equations of motion, which were then solved by means of a modified high precision direct integration method. Furthermore, Lin [27] et al. developed the inverse pseudo-excitation method for dealing with loading identifcation problems. Then, Lin [28] et al. utilized this algorithm to make probabilistic analysis for long-span structures such as longspan bridges [29], non-uniform beams [30] and so on. Other researchers carried out a rigorous series of algorithms in order to improve and develop pseudo-excitation method. Xu [31] et al. presented a new algorithm for buffeting analysis of long span bridges, featured mainly by a complete finite element approach and a pseudo-excitation method and then used this algorithm to make fully coupled buffeting analysis of Tsing Ma suspension bridge [32] and vibration analysis of wind-excited structures [33]. Then, based on the pseudo-excitation method, Xu [34,35] et al. and Zhang [36] et al. also presented closed-form solution for seismic response of adjacent buildings connected by hydraulic actuators with linear quadratic Gaussian (LQG) controllers. Based on the pseudo-excitation method, Sun [37] et al. presented a formulation for fully coupled buffeting analysis of long-span cable-supported bridges, in which dynamic coupling between modes of vibration, dynamic forces on bridge deck and towers and cables, and varying wind speed and structural properties along the bridge deck and towers and cables can be taken into consideration. Li [38] et al. utilized pseudo-excitation method for the random vibration analysis of seismic responses of tall buildings. Xue [39] et al. utilized the pseudo-excitation method to make a random vibration study of structures under multi-component seismic excitations. Li [40] et al. extended the pseudo-excitation method with the stochastic orthogonal polynomial expansion method to make response analysis of stochastic parameter structures under non-stationary random excitation. Nevertheless, the pseudo-excitation method only is utilized to analyze linear structures because this method is derived from superposition principle, which only is applied to linear structures.
In this paper, we construct an approach to calculate the functional reliability, which is denoted as the displacement at the head of gravity dam. The Pseudo excitation method and the response surface method based on weighted regression are associated to analyze the functional reliability of gravity dam. Ultimately, a test example is utilized to verify and analyze the convergence and stability of the proposed method.
2. The Analytical Method for the Functional Reliability
2.1. Brief Introduction on Pseudo Excitation Method
At time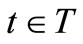 , autocorrelation function of stationary random process
, autocorrelation function of stationary random process  is given by
is given by
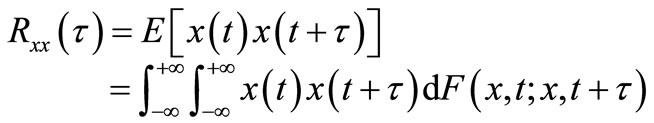 (1)
(1)
where E(#) denotes the expected value of variable #.
Fourier transform pairs are consisted of auto-spectral density function 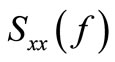 and Autocorrelation function
and Autocorrelation function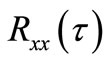 , it can be written as
, it can be written as
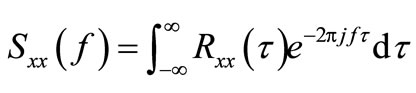 (2)
(2)
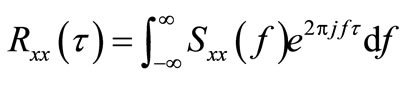 (3)
(3)
From Equations (1)-(3), it can be seen that
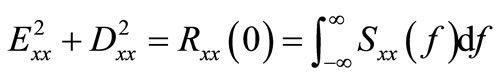 (4)
(4)
where 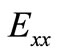 and
and 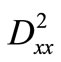 denote the expected value and variance of
denote the expected value and variance of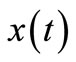 .
.
when  = 0,
= 0,  can be determined from
can be determined from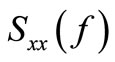 .
.
Pseudo excitation method is the numerical methods for 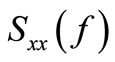 and the basic principle of the pseudo excitation method is depicted as Figure 1.
and the basic principle of the pseudo excitation method is depicted as Figure 1.
Linear system under single-point and stationary random excitation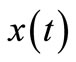 , the response power spectrum of that is written as
, the response power spectrum of that is written as
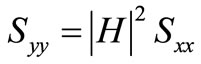 (5)
(5)
This relationship is depicted as Figure 1(a), the meaning of frequency response function H is depicted as Figure 1(b). When the harmonic excitation 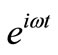 of singlepoint is applied in the linear system, the corresponding response
of singlepoint is applied in the linear system, the corresponding response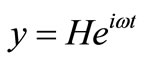 . It is worth noting that pseudo excitation is constructed by excitation, which was
. It is worth noting that pseudo excitation is constructed by excitation, which was 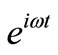 multiplied by constant
multiplied by constant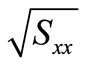 . The pseudo excitation is given by
. The pseudo excitation is given by
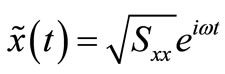 (6)
(6)
The response can also be multiplied by the same constant. It is depicted as Figure 1(c). Still using 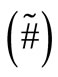 to represent the corresponding pseudo response of variable
to represent the corresponding pseudo response of variable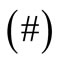 , it should be noted from Figure 1(c) that
, it should be noted from Figure 1(c) that
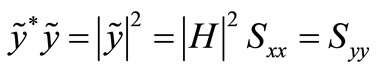 (7)
(7)
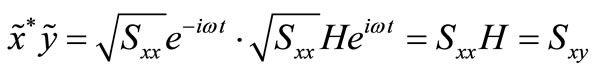 (8)
(8)
 (9)
(9)
where 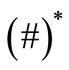 denotes the conjugate of
denotes the conjugate of .
.
If considering two pseudo responses 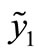 and
and  depict as Figure 1(d), it could be seen that
depict as Figure 1(d), it could be seen that
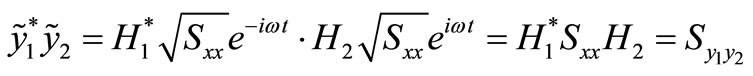 (10)
(10)
 (11)
(11)
From aforementioned analysis, it should be noted that
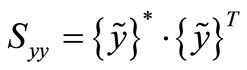 (12)
(12)
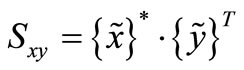 (13)
(13)
 (14)
(14)
Thus it can be obtained that
 (15)
(15)
where f and V denote internal force and displacement, respectively.
2.2. The Method to Calculate the Probabilistic Characteristics
Here, all random variables are assumed to obey Gaussian distribution. Because other distribution form can be translate into Gaussian distribution easily, and Gaussian distribution is extensively applied in the analysis of random variables.
When dam is excited by static and random seismic load, the element’s displacement of dam is random variable. From static analysis of the dam, the expected value  of displacement of element k is obtained. And the variance
of displacement of element k is obtained. And the variance 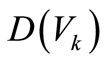 of displacement of element k can be derived as follow.
of displacement of element k can be derived as follow.
The vibration equation of gravity dam is determined as
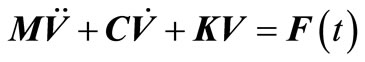 (16)
(16)
where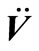 ,
, 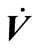 and
and 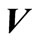 denote acceleration, velocity and displacement of nodes in dam model, respectively;
denote acceleration, velocity and displacement of nodes in dam model, respectively;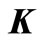 ,
, 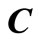 and
and 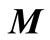 denote stiffness matrix, damping matrix and mass matrix of dam model, respectively;
denote stiffness matrix, damping matrix and mass matrix of dam model, respectively; 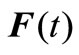 denotes random seismic load.
denotes random seismic load.
From Equation (16), it should be noted that gravity dam under random seismic load is a linear system. Accordingly, the pseudo excitation method can be utilized in aforementioned system.
The pseudo excitation is constructed as
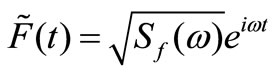 (17)
(17)
where 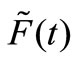 and
and 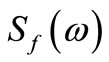 denote pseudo excitation and the power spectrum density of random seismic load, respectively.
denote pseudo excitation and the power spectrum density of random seismic load, respectively.
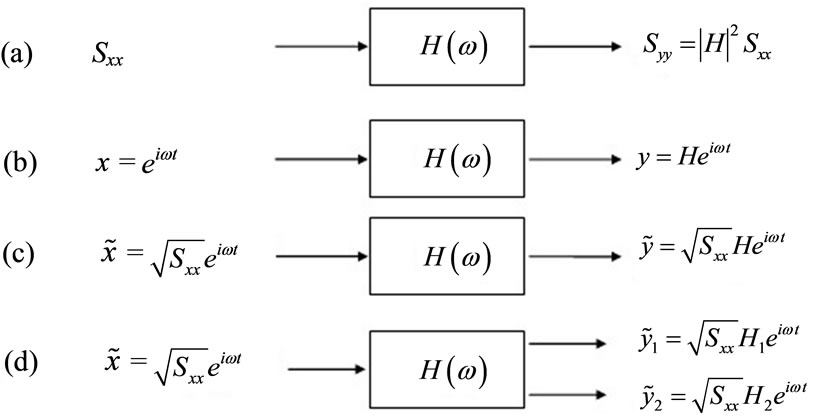
Figure 1. The basic principle of the pseudo excitation method.
Through the pseudo excitation method, the power spectrum density of the displacement of element k is determined as
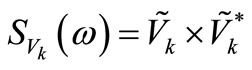 (18)
(18)
where 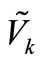 denotes pseudo displacement response of element k.
denotes pseudo displacement response of element k.
Thus the variance  of displacement of element k is given by
of displacement of element k is given by
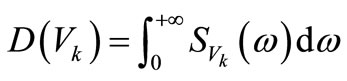 (19)
(19)
2.3. The Method to Calculate the Functional Reliability
The displacement of element k of concrete gravity dam model is taken as functional reliability, and the functional reliability 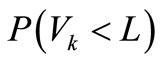 can be decomposed into two parts and expressed as
can be decomposed into two parts and expressed as
 (20)
(20)
where  is the objective displacement.
is the objective displacement. 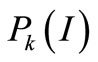 is the probability due to the randomness of the elastic modulus of element k and
is the probability due to the randomness of the elastic modulus of element k and 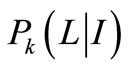 is the conditional probability of element k due to the randomness of seismic load under the condition of these random elastic modulus.
is the conditional probability of element k due to the randomness of seismic load under the condition of these random elastic modulus.
In which
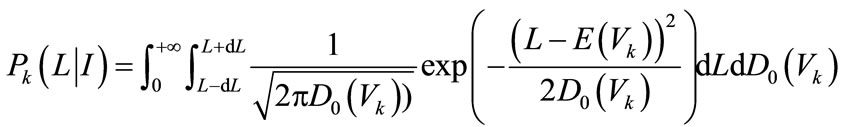 (21)
(21)
where 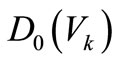 is the objective variance of element k. It can be observed that this expression has considered the randomness of seismic load.
is the objective variance of element k. It can be observed that this expression has considered the randomness of seismic load.
The implicit limited state function 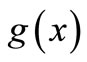 is denoted as the discrepancy between
is denoted as the discrepancy between 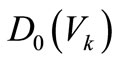 and
and 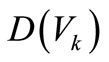 under the condition of random elastic modulus of element k.
under the condition of random elastic modulus of element k.
 (22)
(22)
and 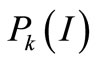 can be derived from the response surface method based on weighted regression [41]. It can be expressed as
can be derived from the response surface method based on weighted regression [41]. It can be expressed as
 (23)
(23)
Ultimately, the functional reliability 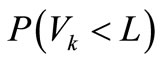 should be derived through above procedure.
should be derived through above procedure.
3. The Numerical Examples for Gravity Dam
The gravity dam is 160 m high. The normal pool level (NPL) is 155 m deep. The level of the back of the dam is 10 m deep. The elevation of upstream and downstream broken-line sloping surface relative to foundation plane are 80 m and 140 m, respectively. The concrete strength of the gravity dam is C20. The finite element model of the gravity dam is divided into 2432 elements. The model consists of 8-node iso-parametric plane elements for the dam and foundation. The density of the dam ρ = 2450 kg/m3, and Poisson ratio v = 0.18. The damping ratio of dam ζ = 0.05. The density of rock foundation ρ = 2700 kg/m3, and Poisson ratio v = 0.25. And the parameters α = 0.9, β = 0.1. Applied load includes gravity load and hydrostatic and uplift pressure and seismic load whose horizontal peak acceleration is 0.25 g. And the objective element k is extracted from one of elements at dam head. The power spectrum density of seismic load is given by
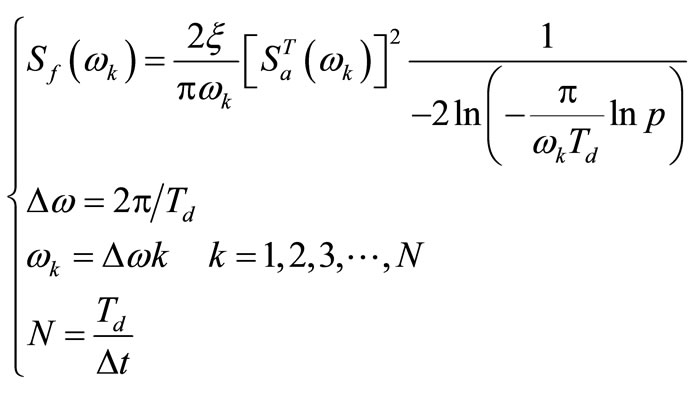 (24)
(24)
where 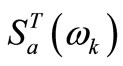 and
and 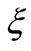 are target response spectrum and damping ratio, respectively;
are target response spectrum and damping ratio, respectively; 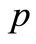 (
(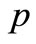 ≤ 0.15) and
≤ 0.15) and  are exceeding response spectrum probability and duration of ground motion, respectively;
are exceeding response spectrum probability and duration of ground motion, respectively; 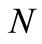 and
and 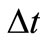 are the number of trigonometric series and time step, respectively.
are the number of trigonometric series and time step, respectively.
Thus, it should be observed that the functional reliability 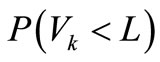 is taken as the reliability for the displacement of gravity dam head. And the displacement of dam head is regarded as the functional reliability of overall gravity dam.
is taken as the reliability for the displacement of gravity dam head. And the displacement of dam head is regarded as the functional reliability of overall gravity dam.
The concrete gravity dam model is shown in Figure 2. The probability distributions of all random parameters of

Figure 2. Sub zone of materials in dam and its foundation.
each element are shown in Table 1.
4. Results and Discussion
The result of 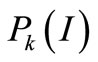 of gravity dam is shown in Table 2. The result of functional reliability
of gravity dam is shown in Table 2. The result of functional reliability 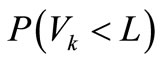 of gravity dam is shown in Table 3. And the deviation factor iterative procedure is shown in Figure 3. The relation between objective variance
of gravity dam is shown in Table 3. And the deviation factor iterative procedure is shown in Figure 3. The relation between objective variance  and the probability
and the probability  is shown in Figure 4. The relation between objective displacement and conditional probability
is shown in Figure 4. The relation between objective displacement and conditional probability 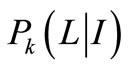 is shown in Figure 5. The relation between objective displacement L and functional reliability
is shown in Figure 5. The relation between objective displacement L and functional reliability 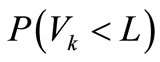 is shown in Figure 6.
is shown in Figure 6.

Table 1. The probability distribution of all random parameters of each element.

Table 2. The result of 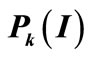 of the displacement of the head of gravity dam.
of the displacement of the head of gravity dam.
In each iterative step of the method of this paper, only 100 experimental points are utilized to approximate implicit limited state function  while the traditional response surface method needs 4865 experimental points. Thus, the method of this paper saves a lot of storage space and can be applied in analyzing large structures such as gravity dams.
while the traditional response surface method needs 4865 experimental points. Thus, the method of this paper saves a lot of storage space and can be applied in analyzing large structures such as gravity dams.
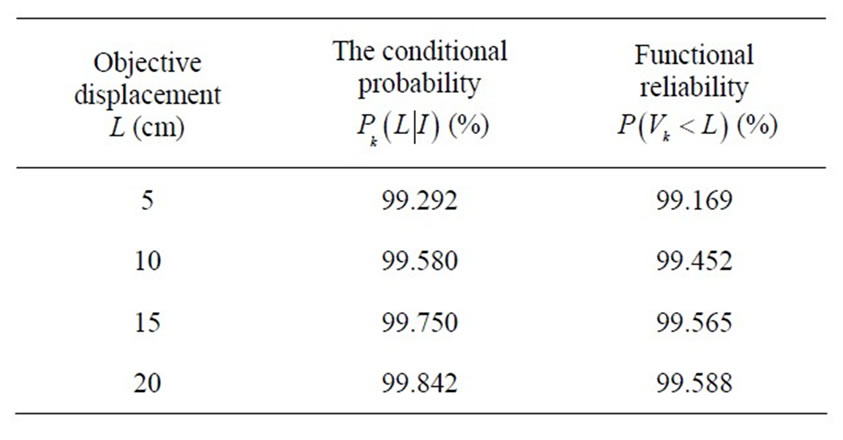
Table 3. Result of functional reliability of the displacement of gravity dam head.
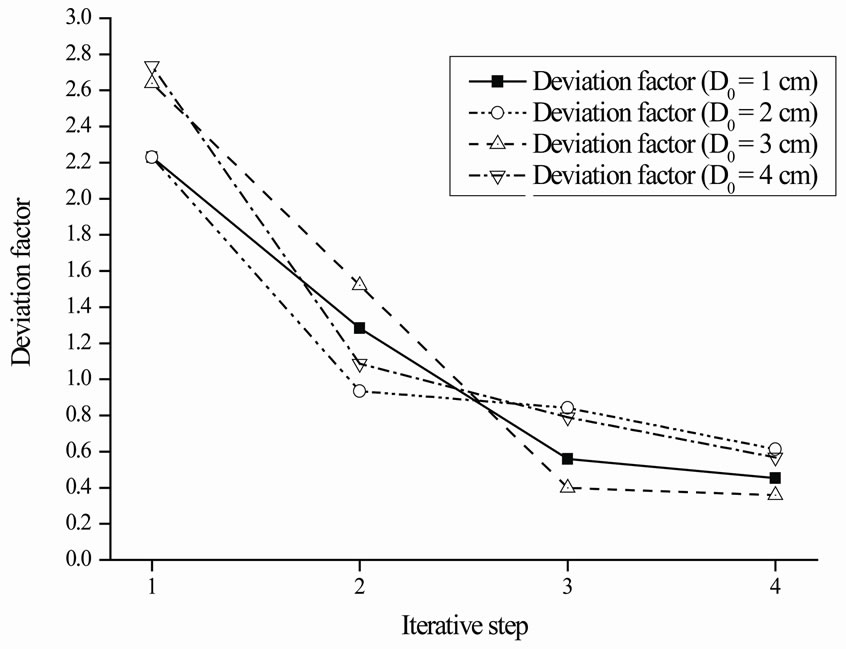
Figure 3. Deviation factor iterative procedure.
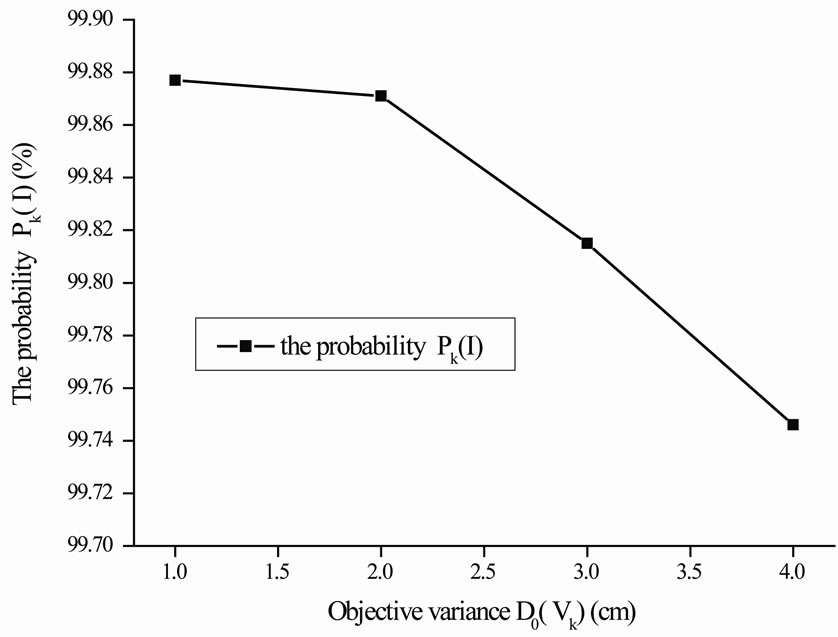
Figure 4. The relation between objective variance  and the probability
and the probability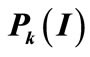 .
.
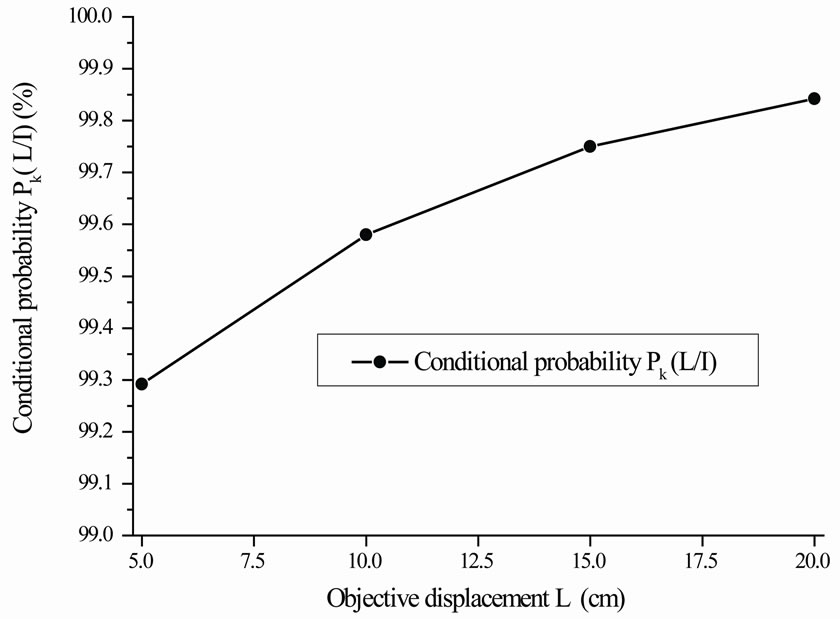
Figure 5. The relation between objective displacement L and conditional probability .
.
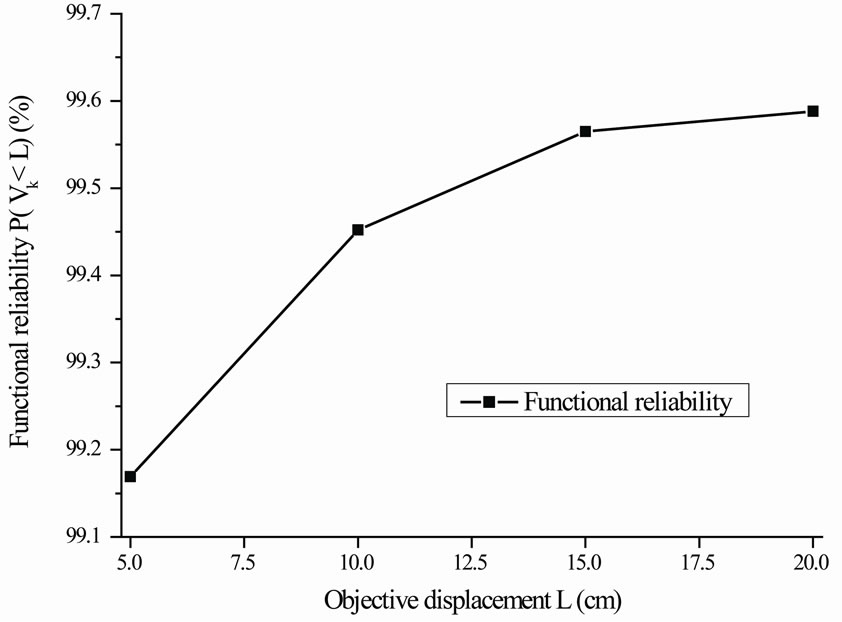
Figure 6. The relation between objective displacement L and functional reliability .
.
From Figure 3, it can be seen that convergence rate of the proposed response surface method based on weighted regression is high. The iteration process achieves stability normally at fourth iteration step. From Figure 4, it can be observed that the probability 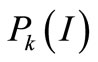 decreases while the objective variance
decreases while the objective variance 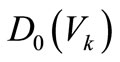 increases and they are substantially appeared inverse proportion relation. From Figure 4, it can be observed that the conditional probability
increases and they are substantially appeared inverse proportion relation. From Figure 4, it can be observed that the conditional probability 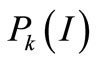 and the functional reliability
and the functional reliability 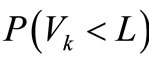 increase while objective displacement L increases and they are obviously exhibited direct proportion relation. Meanwhile, they all appear exponential characteristic.
increase while objective displacement L increases and they are obviously exhibited direct proportion relation. Meanwhile, they all appear exponential characteristic.
From Table 3, it can be seen that the functional reliability of overall gravity dam is 99.169%, 99.452%, 99.565% and 99.588% when the objective displacement is 5 cm, 10 cm, 15 cm and 20 cm, respectively. And it indicates the security of the gravity dam is high.
5. Conclusion
In this paper, we construct an approach to calculate thefunctional reliability, which is denoted as the displacement at the head of gravity dam. The Pseudo excitation method and the response surface method based on weighted regression are associated to analyze the functional reliability of gravity dam. Ultimately, a test example is utilized to verify and analyze the convergence and stability of the proposed method.
6. Acknowledgements
This study was supported by Project supported by the National Natural Science Foundation of China (Grant No. 51109029, 51178081, 51138001, 50909015, 51009020). and China Postdoctoral Science Foundation (Grant No. 20110491535).
REFERENCES
- Y. W Liu and F. Moses, “A Sequential Response Surface Method and Its Application in the Reliability Analysis of Aircraft Structural System,” Structural Safety, Vol. 16, No. 1-2, 1994, pp. 39-46. doi:10.1016/0167-4730(94)00023-J
- L. J. Moore and P. Sa, “Comparisons with the Best in Response Surface Methodology,” Statistics & Probability, Vol. 44, No. 2, 1999, pp. 189-194.
- Y. Zheng and P. K. Das, “Improved Response Surface Method and Its Application to Stiffened Plate Reliability Analysis,” Engineering Structures, Vol. 22, No. 5, 2000, pp. 544-551. doi:10.1016/S0141-0296(98)00136-9
- X. L. Guan and R. E. Melchers, “Effect of Response Surface Parameter Variation on Structural Reliability Estimates,” Structural Safety, Vol. 23, No. 4, 2001, pp. 429-444. doi:10.1016/S0167-4730(02)00013-9
- B. D. Youn and K. K. Choi, “A New Response Surface Methodology for Reliability-Based Design Optimization,” Computers and Structures, Vol. 82, No. 2-3, 2004, pp. 241-256. doi:10.1016/j.compstruc.2003.09.002
- S. Gupta and C. S. Manohar, “Improved Response Surface Method for Time Variant Reliability Analysis of Nonlinear Random Structures under Non-Stationary Excitations,” Nonlinear Dynamics, Vol. 36, No. 2-4, 2004, pp. 267-280. doi:10.1023/B:NODY.0000045519.49715.93
- H. M. Gomes and A. M. Awruch, “Comparison of Response Surface and Neural Network with Other Methods for Structural Reliability Analysis,” Structural Safety, Vol. 26, No. 1, 2004, pp. 49-67. doi:10.1016/S0167-4730(03)00022-5
- I. Kaymaz and C. A. McMahon, “A Response Surface Method Based on Weighted Regression for Structural Reliability Analysis,” Probabilistic Engineering Mechanics, Vol. 20, No. 1, 2005, pp. 11-17. doi:10.1016/j.probengmech.2004.05.005
- S. M. Wong, R. E. Hobbs and C. Onof, “An Adaptive Response Surface Method for Reliability Analysis of Structures with Multiple Loading Sequences,” Structural Safety, Vol. 27, No. 4, 2005, pp. 287-308. doi:10.1016/j.strusafe.2005.02.001
- J. Q. Jiang, C. G. Wu, C. Y. Song, et al., “Adaptive and Iterative Gene Selection Based on Least Squares Support Vector Regression,” Journal of Information & Computational Science, Vol. 3, 2006, pp. 443-451. doi:10.1109/GRC.2008.4664732
- W.-L. Jin and X.-X. Yuan, “Response Surface Method Based on LS-SVM for Structural Reliability Analysis,” Journal of Zhejiang University (Engineering Science), Vol. 41, No. 1, 2007, pp. 44-47.
- M. S. Chebbah, “Response Surface Method for the Rapid Design of Process Parameters in Tube Hydroforming,” Material Processing and Design, Vol. 7, 2007, pp. 455-460. doi:10.1063/1.2740853
- J. Cheng, Q. S. Li and R.-C. Xiao, “A New Artificial Neural Network-Based Response Surface Method for Structural Reliability Analysis,” Probabilistic Engineering Mechanics, Vol. 23, No. 1, 2008, pp. 51-63. doi:10.1016/j.probengmech.2007.10.003
- H. P. Gavin and S. C. Yau, “High-Order Limit State Functions in the Response Surface Method for Structural Reliability Analysis,” Structural Safety, Vol. 30, No. 2, 2008, pp. 162-179. doi:10.1016/j.strusafe.2006.10.003
- T. Zou, Z. P. Mourelatos, Z. P. Mourelatos and J. Tu, “An Indicator Response Surface Method for Simulation-Based Reliability Analysis,” Journal of Mechanical Design, Vol. 130, No. 7, 2008, pp. 1-11. doi:10.1115/1.2918901
- X. S. Nguyen, A. Sellier, F. Duprat and G. Pons, “Adaptive Response Surface Method Based on a Double Weighted Regression Technique,” Probabilistic Engineering Mechanics, Vol. 24, No. 2, 2009, pp. 135-143. doi:10.1016/j.probengmech.2008.04.001
- Y. J. Hong, J. Xing and J. B. Wang, “A Second-Order Third-Moment Method for Calculating the Reliability of Fatigue,” International Journal of Pressure Vessels and Piping, Vol. 76, No. 8, 1999, pp. 567-570. http://dx.doi.org/10.1016/S0308-0161(99)00013-7
- A. Der Kiureghian and T. Dakessian, “Multiple Design Points in First and Second-Order Reliability,” Structural Safety, Vol. 20, No. 1, 1998, pp. 37-49. doi:10.1016/S0167-4730(97)00026-X
- H. U. Koyluoglu and S. R. K. Nielsen, “New Approximations for SORM Integrals,” Structural Safety, Vol. 13, No. 4, 1994, pp. 235-246. doi:10.1016/0167-4730(94)90031-0
- C. C. Qiu and M. E. Orazem, “A Weighted Nonlinear Regression-Based Inverse Model for Interpretation of Pipeline Survey Data,” Electrochimica Acta, Vol. 49, No. 22-23, 2004, pp. 3965-3975. http://dx.doi.org/10.1016/j.electacta.2004.03.045
- K. Triantafyllopoulos, “Multivariate Discount Weighted Regression and Local Level Models,” Computational Statistics & Data Analysis, Vol. 50, No. 12, 2006, pp. 3702- 3720. doi:10.1016/j.csda.2005.07.003
- J. Zhao and Z. Z. Lu, “Response Surface Method for Reliability Analysis of Implicit Limit State Equation Based on Weighted Regression,” Journal of Mechanical Strength, Vol. 28, No. 4, 2006, pp. 512-516.
- A. D. Kiureghian and A. Neuenhofer, “Response Spectrum Method for Muti-Support Seismic Excitation,” Earthquake Engineering & Structural Dynamics, Vol. 21, No. 1, 1992, pp. 713-740. doi:10.1002/eqe.4290210805/abstract
- H. Z. Ernesto and E. H Vanmarcke, “Seismic Random Vibration Analysis of Multi-Support Structural Systems,” Journal of Engineering Mechanics, Vol. 120, No. 5, 1994, pp. 1107-1128. doi:10.1061/(ASCE)0733-9399(1994)120:5(1107)
- J. H. Lin, “A Fast CQC Algorithm of PSD Matrices for Random Seismic Responses,” Computers & Structures, Vol. 44, No. 3, 1992, pp. 683-687. doi:10.1016/0045-7949(92)90401-K
- J. H. Lin, W. P. Shen and F. W. Williams, “Accurate High- Speed Computation of Non-Stationary Random Structural Response,” Engineering Structures, Vol. 19, No. 7, 1997, pp. 586-593. doi:10.1016/S0141-0296(97)83154-9
- J. H. Lin, X. L. Guo, H. Zhi, W. P. Howson and F. W. Williams, “Computer Simulation of Structural Random Loading Identifcation,” Computers and Structures, Vol. 79, No. 4, 2001, pp. 375-387. doi:10.1016/S0045-7949(00)00154-1
- J. H. Lin, Y. Zhao and Y. H. Zhang, “Accurate and Highly Efficient Algorithms for Structural Stationary/Non-Stationary Random Responses,” Computer Methods in Applied Mechanics and Engineering, Vol. 191, No. 1-2, 2001, pp. 103-111. doi:10.1016/S0045-7825(01)00247-X
- J. H. Lin, Y. H. Zhang, Q. S. Li and F. W. Williams, “Seismic Spatial Effects for Long-Span Bridges, Using the Pseudo Excitation Method,” Engineering Structures, Vol. 26, No. 9, 2004, pp. 1207-1216. doi:10.1016/j.engstruct.2004.03.019
- J. H. Lin, G. Z. Song and Y. Sun, “Non-Stationary Random Seismic Responses of Non-Uniform Beams,” Soil Dynamics and Earthquake Engineering, Vol. 14, No. 4, 1995, pp. 301-306. doi:10.1016/0267-7261(94)00030-K
- Y. L. Xu, D. K. Sun, J. M. Ko and J. H. Lin, “Buffeting Analysis of Long Span Bridges: A New Algorithm,” Computers and Structures, Vol. 68, No. 4, 1998, pp. 303- 313. doi:10.1016/S0045-7949(98)00072-8
- Y. L. Xu, D. K. Sun, J. M. Ko and J. H. Lin, “Fully Coupled Buffeting Analysis of Tsing Ma Suspension Bridge,” Journal of Wind Engineering and Industrial Aerodynamics, Vol. 85, No. 1, 2000, pp. 97-117. doi:10.1016/S0167-6105(99)00133-6
- Y. L. Xu, W. S. Zhang, J. M. Ko and J. H. Lin, “PseudoExcitation Method for Vibration Analysis of Wind-Excited Structures,” Journal of Wind Engineering and Industrial Aerodynamics, Vol. 83, No. 1-3, 1999, pp. 443-454. doi:10.1016/S0167-6105(99)00092-6
- Y. L. Xu and W. S. Zhang, “Closed-Form Solution for Seismic Response of Adjacent Buildings with Linear Quadratic Gaussian Controllers,” Earthquake Engineering & Structural Dynamics, Vol. 31, No. 2, 2002, pp. 235-259. doi:10.1002/eqe.107
- Y. L. Xu, Q. He and J. M. Ko, “Dynamic Response of Damper-Connected Adjacent Buildings under Earthquake Excitation,” Engineering Structures, Vol. 21, No.1, 1999, pp. 135-148. doi:10.1016/S0141-0296(97)00154-5
- W. S. Zhang and Y. L. Xu, “Dynamic Characteristics and Seismic Response of Adjacent Buildings Linked by Discrete Dampers,” Earthquake Engineering & Structural Dynamics, Vol. 28, No. 10, 1999, pp. 1163-1185. doi:/10.1002/(SICI)1096-9845(199910)28:10<1163::AID-EQE860>3.0.CO;2-0
- D. K. Sun, Y. L. Xu, J. M. Ko and J. H. Lin, “Fully Coupled Buffeting Analysis of Long-Span Cable-Supported Bridges: Formulation,” Journal of Sound and Vibration, Vol. 228, No. 3, 1999, pp. 569-588. doi:10.1006/jsvi.1999.2425
- Q. S. Li, Y. H. Zhang, J. R. Wua and J. H. Lin, “Seismic Random Vibration Analysis of Tall Buildings,” Engineering Structures, Vol. 26, No. 12, 2004, pp. 1767-1778. doi:10.1016/j.engstruct.2004.06.013
- S. D. Xue, Z. Cao and X. S. Wang, “Random Vibration Study of Structures under Multi-Component Seismic Excitations,” Advances in Structural Engineering, Vol. 5, No. 3, 2002, pp. 185-192. doi:10.1260/136943302760228130
- J. Li and S. T. Liao, “Response Analysis of Stochastic Parameter Structures under Non-Stationary Random Excitation,” Computational Mechanics, Vol. 27, No. 1, 2001, pp. 61-68. doi:10.1007/s004660000214
- J. Y. Chen, Q. Xu, J. Li and S. L. Fan, “Improved Response Surface Method for Anti-Slide Reliability Analysis of Gravity Dam Based on Weighted Regression,” Journal of Zhejiang University—Science A (Applied Physics & Engineering), Vol. 11, No. 6, 2010, pp. 432- 439. doi:10.1631/jzus.A0900709
NOTES
*Corresponding author.

