Journal of Water Resource and Protection
Vol.5 No.1(2013), Article ID:26987,5 pages DOI:10.4236/jwarp.2013.51002
An Interval-parameter Fuzzy Robust Nonlinear Programming Model for Water Quality Management*
1MOE Key Laboratory of Regional Energy Systems Optimization, North China Electric Power University, Beijing, China
2College of Environmental Science and Engineering, North China Electric Power University, Beijing, China
3Environmental Systems Engineering Program, Faculty of Engineering, University of Regina, Regina, Canada
4College of Economic and Management, North China Electric Power University, Beijing, China
Email: liumin-224@163.com, zhuimeng_211@126.com
Received October 14, 2012; revised November 18, 2012; accepted November 28, 2012
Keywords: Water Quality Management; Interval Programming; Fuzzy Robust Programming; Nonlinear Programming; Uncertainty
ABSTRACT
Planning for water quality management is important for facilitating sustainable socio-economic development; however, the planning is also complicated by a variety of uncertainties and nonlinearities. In this study, an interval-parameter fuzzy robust nonlinear programming (IFRNP) model was developed for water quality management to deal with such difficulties. The developed model incorporated interval nonlinear programming (INP) and fuzzy robust programming (FRP) methods within a general optimization framework. The developed IFRNP model not only could explicitly deal with uncertainties represented as discrete interval numbers and fuzzy membership functions, but also was able to deal with nonlinearities in the objective function.
1. Introduction
Water is one of the most important natural resources, and can provide support to human survival, sustainable socioeconomic development, and ecosystem preservation. However, in recent years, due to speedy population growth and rapid socio-economic development throughout the world, many challenging water resources problems, such as water quality deterioration and water shortage, have caused widespread concerns. Water quality deterioration can lead to various adverse impacts on human health, environment, and industrial and agricultural production. Therefore, effective planning for water quality management is desired. However, water quality management is inevitably complicated since it involves in a variety of uncertainties and nonlinearities. For example, dynamic interactions, associated with a variety of uncertainties, exist between pollutant loadings and receiving waters [1,2]; uncertainties exist in many system components, and can affect the related decision processes [3]; moreover, representation of system costs for water quality management involves a number of nonlinear functions for projecting the interrelationships between environment and economy [4]. Such complexities lead to difficulties in formulating and solving the resulting optimization problems.
As a result, various research efforts were made for dealing with the above difficulties in water quality management through interval nonlinear programming (INP) [5], stochastic nonlinear programming (SNP) [6], and fuzzy nonlinear programming (FNP) [7]. The uncertainties were expressed as interval ranges, probability density functions, and fuzzy membership functions, respectively. In INP models, interval numbers are acceptable for the uncertain inputs under an implicit distribution assumption, and the distribution information for model parameters is not required. SNP models can deal with various probabilistic uncertainties; however, the increased data requirements for specifying the parameters’ probability distributions may affect their practical applicability. FNP models can facilitate the analysis of systems with uncertainties being derived from vagueness or fuzziness, and be suitable for the situations that the uncertainties can not be expressed as interval numbers and probability density functions. Although each method can prove effectiveness in dealing with uncertainties expressed in a single format, it is confronted with difficulties when multiple uncertainties exist. In real-world problems, water quality management is associated with various uncertainties, and multiple formats of uncertainties need be investigated in the processes of problem definition as well as model formulation and solution. Therefore, an integrated inexact nonlinear programming model is desired for water quality management.
For water quality management problems, many studies for integrated inexact nonlinear programming models have been made. For instance, Li et al. [8] developed an interval-fuzzy two-stage quadratic programming method, which incorporated interval-parameter programming, twostage stochastic programming, and fuzzy quadratic programming with a general optimization framework; Luo et al. [9] proposed an inexact two-stage stochastic nonlinear programming model, where uncertainties were expressed as intervals numbers and probability density functions; Qin et al. [4] developed an interval-parameter fuzzy nonlinear programming (IFNP) model, which was a hybrid of INP and FNP. IFNP model is effective in dealing with uncertainties expressed as discrete intervals and/or fuzzy membership functions; however, it is incapable of dealing with fuzziness in the left-hand-side coefficients of the constraints. In contrast, fuzzy robust programming (FRP) can effectively reflect the conditions when uncertainties in both leftand right-hand-side coefficients of the constraints are only expressed as fuzzy membership functions [10].
Therefore, as an extension of previous studies, an interval-parameter fuzzy robust programming (IFRNP) model is developed for water quality management, where techniques of INP and FRP are incorporated within a general optimization framework. The developed IFRNP model can address multiple uncertainties associated with nonlinear functions.
2. Modeling Formulation
Planning for water quality management is related to many socio-economic and environmental factors. The IFRNP model is formulated to minimize the system cost of wastewater treatment, and it is consist of a nonlinear objective function and a set of water quality constraints.
2.1. Water Quality Simulation Model
Previously, many water quality simulation models, such as the Streeter-Phelps, O’Conner, Dobbins and Thomas models, have been developed into useful tools for supporting environmental management. In this study, the Streeter-Phelps model is used to quantify water quality constraints related to biological oxygen demand (BOD) and dissolved oxygen (DO) discharges as well as their concentrations in stream waters.
According to conservation of mass, the basic equations of the Streeter-Phelps model can be written:
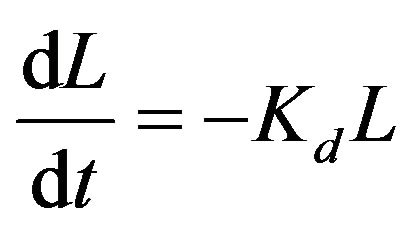 (1a)
(1a)
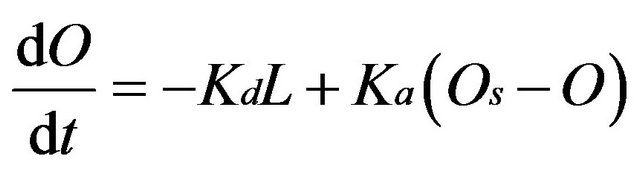 (1b)
(1b)
where L and O are the ultimate BOD and DO concentrations, respectively; Os is the saturated DO concentration; Kd and Ka are the first-order deoxygenation and reaeration rate constants, respectively; t is the mean flow time. So the solutions of Equations (1a) and (1b) are:
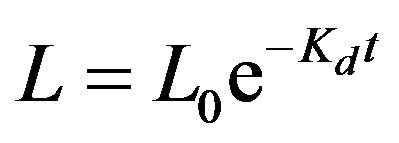 (2a)
(2a)
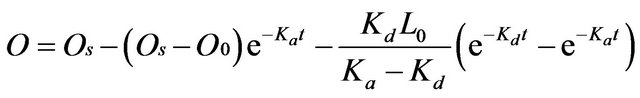 (2b)
(2b)
where L0 and O0 are BOD and DO concentrations at the starting point of the stream system, respectively.
Segmentation is necessary since a number of wastewater discharge outlets scatter along the stream, with temporal and spatial variations of their loadings. Water quality at each section is affected by various sources from the upper stream.
According to the previous study [4], a matrix expression for water quality prediction can be established:
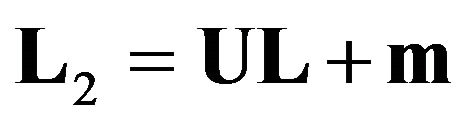 (3a)
(3a)
 (3b)
(3b)
where U, V and R are n × n transformation matrixes; m and n are n-dimensional transformation vectors; L and O are n-dimensional transformation vectors associating with the observed BOD and DO loads in wastewater sources, respectively; L2 and O2 are n-dimensional transformation vectors associating with the predicted BOD and DO levels at different stream segments, respectively.
2.2. Optimization Model Formulation
The operating cost functions for handling different types of wastewater have different expressions. They are normally expressed in various empirical formulations [4]. In China, the most widely used function for reflecting the operational cost of a wastewater treatment unit can be expressed:
 (4)
(4)
where C is the wastewater treatment cost; Q is the wastewater discharge rate; η is the wastewater treatment efficiency, 0 ≤ η ≤ 1; K1 and K3 are the cost-function coefficients, K1, K3 > 0; K2 is the economy-of-scale index of treatment cost, 0 < K2 < 1; K4 is the scale index of treatment efficiency, K4 > 1.
For a water quality management system containing n industries (i.e., wastewater discharger sources), a deterministic optimization model can be formulated as follows:
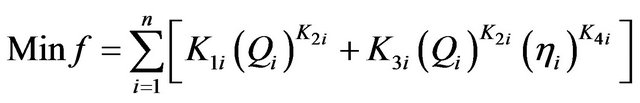 (5a)
(5a)
Subject to:
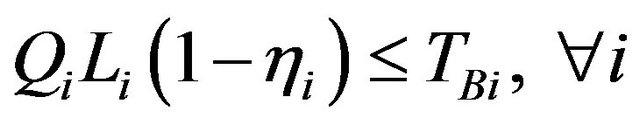 (5b)
(5b)
 (5c)
(5c)
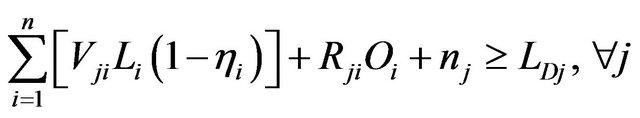 (5d)
(5d)
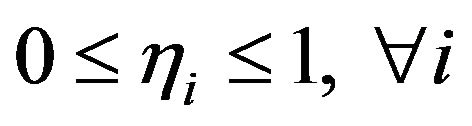 (5e)
(5e)
where f is the wastewater treatment cost; i denotes the name of wastewater discharge sources; j denotes the index of stream segments. Uji, Vji and Rji are the elements of transformation matrices; mj and nj are the elements of transformation vectors; Li and Oi are the elements of raw BOD and DO concentration vectors, respectively; TBi are the elements of BOD discharge allowances vectors; LCj and LDj are the elements of water quality standards vectors for BOD and DO, respectively.
Model (5a)-(5e) describes the relationships between economical and environmental factors involved in water quality management. However, a number of parameters in the optimization model may not be deterministic due to the existence of uncertainties [11]. Some parameters, such as wastewater discharge rate and wastewater treatment efficiency, may be represented as discrete intervals; raw BOD and DO concentrations in wastewater and environmental requirements for BOD and DO discharge may be expressed as fuzzy values, where the L-R fuzzy membership functions are taken for the fuzzy boundaries. So an IFRNP model is formulated:
 (6a)
(6a)
Subject to:
 (6b)
(6b)
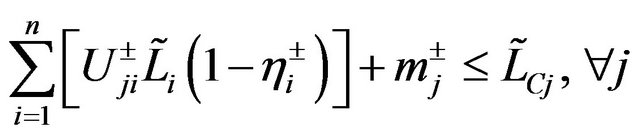 (6c)
(6c)
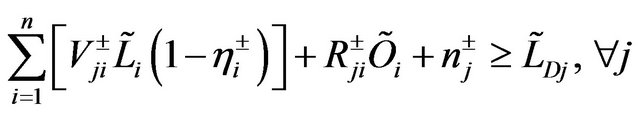 (6d)
(6d)
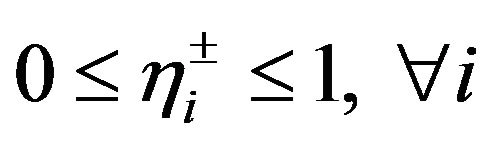 (6e)
(6e)
where f±, 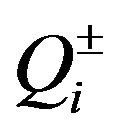 and
and 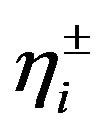 denote a set of interval numbers with deterministic lower and upper bounds;
denote a set of interval numbers with deterministic lower and upper bounds;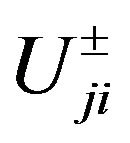 ,
, 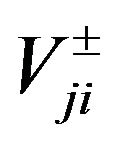 and
and 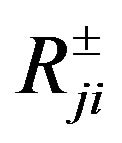 denote the elements of intervals matrixes;
denote the elements of intervals matrixes; 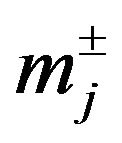 and
and 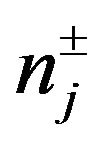 denote the elements of intervals vectors;
denote the elements of intervals vectors;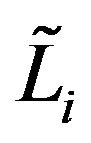 ,
, 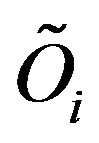 ,
, 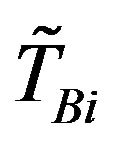 ,
, 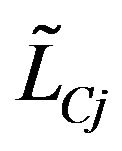 and
and  denote the elements of a set of fuzzy vectors.
denote the elements of a set of fuzzy vectors.
3. Solution Methods
The operating cost function (6a) can be generalized into:
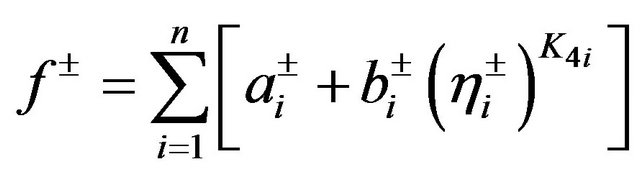 (7)
(7)
According to the previous study [12], by taking the method of the piecewise linearization, Equation (7) can be converted into:
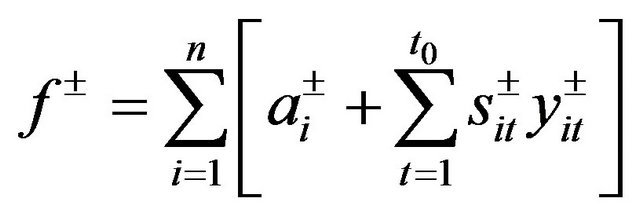 (8a)
(8a)
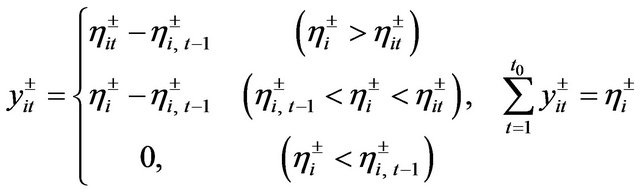 (8b)
(8b)
where 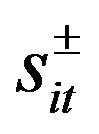 and
and  are a set of interval numbers associating with the relevant slopes of straight line and the wastewater efficiency, respectively; t is the number of segments. So models (6a)-(6e) can be converted into:
are a set of interval numbers associating with the relevant slopes of straight line and the wastewater efficiency, respectively; t is the number of segments. So models (6a)-(6e) can be converted into:
 (9a)
(9a)
Subject to:
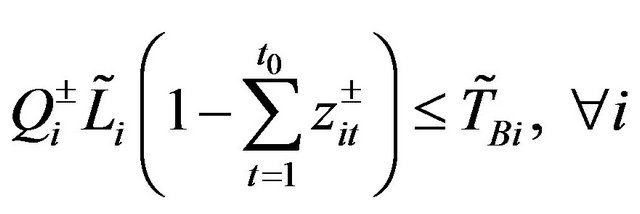 (9b)
(9b)
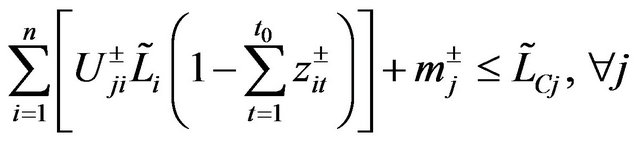 (9c)
(9c)
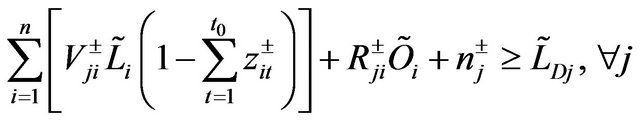 (9d)
(9d)
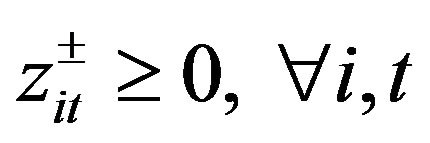 (9e)
(9e)
where  and
and 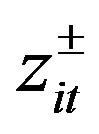 are a set of interval numbers associating with the relevant slopes of straight line and the wastewater efficiency, respectively.
are a set of interval numbers associating with the relevant slopes of straight line and the wastewater efficiency, respectively.
This IFRNP problem is converted into an interval-parameter fuzzy robust linear programming (IFRLP) problem through the piecewise linearization approach. Then the IFRLP problem can be solved within an ILP framework by utilizing FRLP optimization techniques.
According to the algorithms proposed by Huang et al. [13,14], the solution for models (9a)-(9e) can be obtained through a two-step method, where a submodel corresponding to f– is first formulated and solved, and then the relevant submodel corresponding to f+ can be formulated based on the solution of the first submodel. In detail, the first submodel can be formulated as follows:
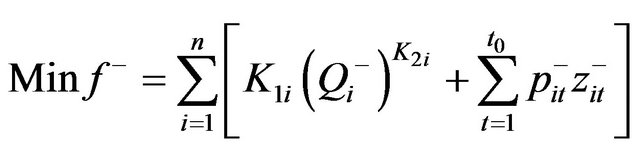 (10a)
(10a)
Subject to:
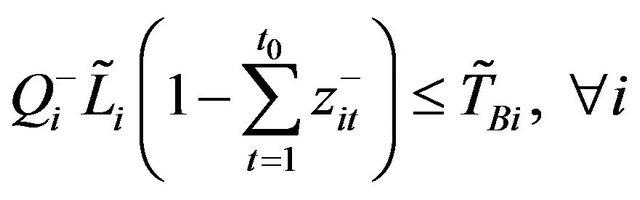 (10b)
(10b)
 (10c)
(10c)
 (10d)
(10d)
 (10e)
(10e)
Thus, solutions of 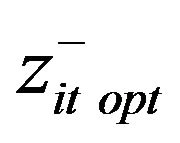 can be obtained, and then the submodel corresponding to f+ can be formulated as follows:
can be obtained, and then the submodel corresponding to f+ can be formulated as follows:
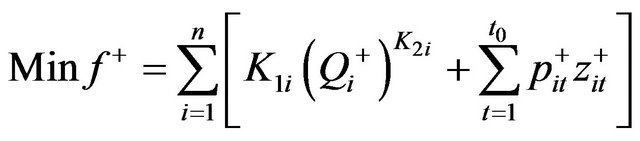 (11a)
(11a)
Subject to:
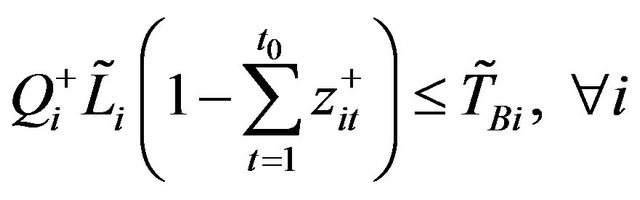 (11b)
(11b)
 (11c)
(11c)
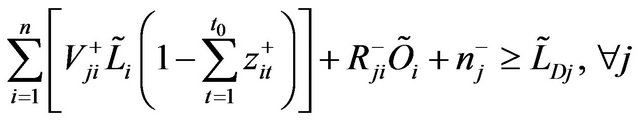 (11d)
(11d)
 (11e)
(11e)
 (11f)
(11f)
Uncertainties still exist in these two submodels due to the fuzzy constraints (10b)-(10d) and (11b)-(11d). FRLP techniques are desired in the solution process to tackle fuzziness in the leftand right-hand sides of model’s constraints. According to the concept of level set and representation theorem [10], (10b)-(10d) and (11b)-(11d) can be respectively concerted into:
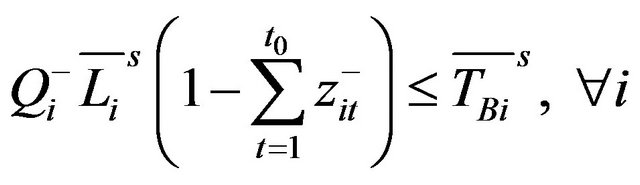 (10b’)
(10b’)
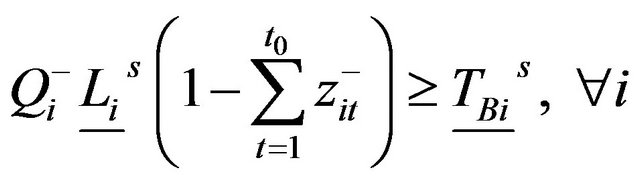 (10b”)
(10b”)
 (10c’)
(10c’)
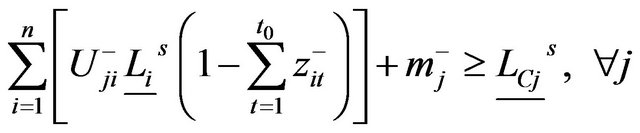 (10c”)
(10c”)
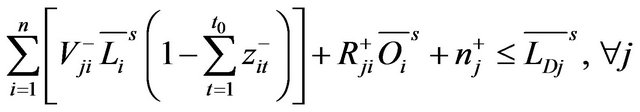 (10d’)
(10d’)
 (10d”)
(10d”)
and
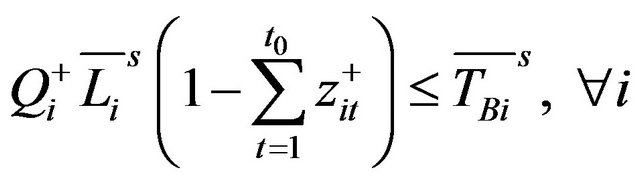 (11b’)
(11b’)
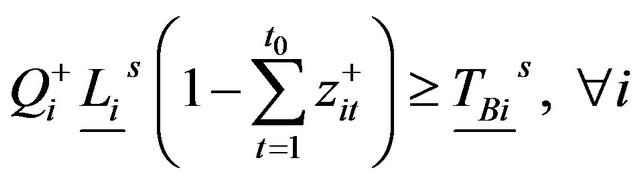 (11b”)
(11b”)
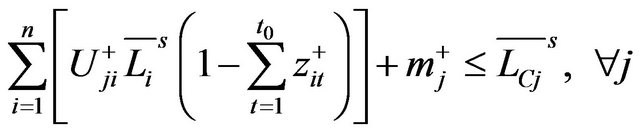 (11c’)
(11c’)
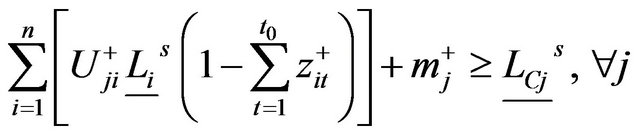 (11c”)
(11c”)
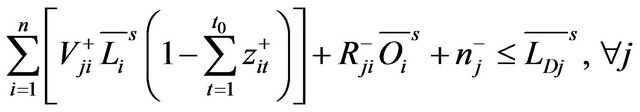 (11d’)
(11d’)
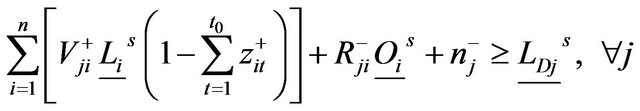 (11d”)
(11d”)
where the marks “–s” and “_s” denote the superior and inferior limits among the set s.
Following these decomposition and replacements, the final solutions for model (9a-9e) as 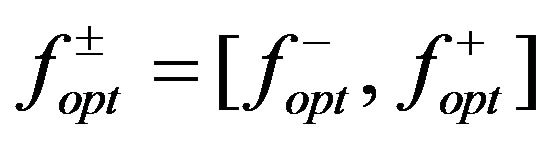 and
and 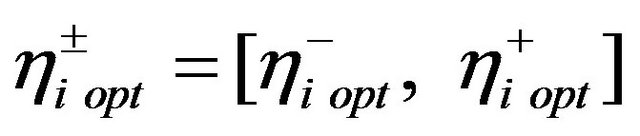 can be obtained.
can be obtained.
4. Conclusions
In this study, an interval-parameter fuzzy robust nonlinear programming (IFRNP) model was developed for water quality management under uncertainty. As an integration of interval nonlinear programming (INP) and fuzzy robust programming (FRP), the developed IFRNP model could explicitly address the complexities of various system uncertainties, where parameters were represented as interval numbers and/or fuzzy membership functions; moreover, it could deal with the nonlinearities in the objective function.
The method of piecewise linearization was developed to deal with the nonlinear cost function in the IFRNP model. Such a linearization approach was suitable for nonlinear functions; however, the approach could be further improved by 0 - 1 piecewise linearization approach. Moreover, other inexact optimization methods, such as stochastic programming and multi-objective programming, could be incorporated into IFRNP model to handle various types of uncertainties and enhance the model’s application.
5. Acknowledgements
This research was supported by the Major Science and Technology Program for Water Pollution Control and Treatment (2009ZX07104-004). The authors are very grateful to the editors and the anonymous reviewers for their insightful comments and suggestion.
REFERENCES
- H. Hoppe, M. Weilandt and H. Orth, “A Combined Water Management Approach Based on River Water Quality Standards,” Journal of Environmental Informatics, Vol. 3, No. 2, 2004, pp. 67-76. doi:10.3808/jei.200400028
- Y. P. Li, G. H. Huang and S. L. Nie, “Optimization of Regional Economic and Environmental Systems under Fuzzy and Random Uncertainties,” Journal of Environmental Management, Vol. 92, No. 8, 2011, pp. 2010-2020. doi:10.1016/j.jenvman.2011.03.022
- Y. P. Li, G. H. Huang, S. L. Nie and D. W. Mo, “IntervalParameter Robust Quadratic Programming for Water Quality Management under Uncertainty,” Engineering Optimization, Vol. 40, No. 7, 2008, pp. 613-635. doi:10.1080/03052150801918347
- X. S. Qin, G. H. Huang, G. M. Zeng, A. Chakma and Y. F. Huang, “An Interval-Parameter Fuzzy Nonlinear Optimization Model for Stream Water Quality Management under Uncertainty,” European Journal of Operational Research, Vol. 180, No. 3, 2007, pp. 1331-1357. doi:10.1016/j.ejor.2006.03.053
- M. J. Chen and G. H. Huang, “A Derivative Algorithm for Inexact Quadratic Program-Application to Environmental Decision-Making under Uncertainty,” European Journal of Operation Research, Vol. 128, No. 3, 2001, pp. 570-586. doi:10.1016/S0377-2217(99)00374-4
- M. V. F. Pereira and L. M. V. G. Pinto, “Multi-Stage Stochastic Optimization Applied to Energy Planning,” Mathematics Programming, Vol. 52, No. 1-3, 1991, pp. 359- 375. doi:10.1007/BF01582895
- H. W. Chen and N. B. Chang, “Water Pollution Control in the River Basin by Fuzzy Genetic Algorithm-Based Multi Objective Programming Modeling,” Water Science and Technology, Vol. 37, No. 8, 1998, pp. 55-63. doi:10.1016/S0273-1223(98)00258-3
- Y. P. Li, G. H. Huang and N. L. Nie, “IFTSQP: An Inexact Optimization Model for Water Resources Management under Uncertainty,” Water International, Vol. 32, No. 3, 2007, pp. 439-456. doi:10.1080/02508060708692223
- B. Luo, I. Maqsood, Y. Y. Yin, G. H. Huang and S. J. Cohen, “Adaption to Climate Change through Water Trading under Uncertainty: An Inexact Two-Stage Nonlinear Programming Approach,” Journal of Environmental Informatics, Vol. 2, No. 2, 2003, pp. 58-68. doi:10.3808/jei.200300022
- L. Liu, G. H. Huang, Y. Liu, G. A. Fuller and G. M. Zeng, “A Fuzzy-Stochastic Robust Programming Model for Regional Air Quality Management under Uncertainty,” Engineering Optimization, Vol. 35, No. 2, 2003, pp. 177-199. doi:10.1080/0305215031000097068
- G. H. Huang and N. B. Chang, “Perspectives of Environmental Informatics and Systems Analysis,” Journal of Environmental Informatics, Vol. 1, No. 1, 2003, pp. 1-6. doi:10.3808/jei.200300001
- H. Zhu, G. H. Huang, P. Guo and X. S. Qin, “A Fuzzy Robust Nonlinear Programming Model for Stream Water Quality Management,” Water Resource Management, Vol. 23, No. 14, 2009, pp. 2913-2940. doi:10.1007/s11269-009-9416-3
- G. H. Huang, B. W. Baetz and G. G. Patry, “A Grey Linear Programming Approach for Municipal Solid Waste Management Planning under Uncertainty,” Civil Engineering Systems, Vol. 9, No. 4, 1992, pp. 319-335. doi:10.1080/02630259208970657
- G. H. Huang, B. W. Baetz and G. G. Patry, “Grey Fuzzy Integer Programming: An Application to Regional Waste Management Planning under Uncertainty,” Socio-Economic Planning Science, Vol. 29, No. 1, 1995, pp. 17-38.
NOTES
*Major Science and Technology Program for Water Pollution Control and Treatment (2009ZX07104-004).

