Communications and Network
Vol.08 No.02(2016), Article ID:66376,12 pages
10.4236/cn.2016.82008
Protection Strategies against Cascading Failure for Power Systems of Ring Network
Arun Kumar1, Hnin Yu Shwe1, Peter Han Joo Chong2
1School of Electrical & Electronic Engineering, Nanyang Technological University, Singapore
2Department of Electrical and Electronic Engineering, Auckland University of Technology, Auckland, New Zealand
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 March 2016; accepted 9 May 2016; published 12 May 2016
ABSTRACT
Power grid vulnerability is a key issue with large blackouts, causing power disruption for millions of people. The complexity of power grid, together with excessive number of components, makes it difficult to be modeled. Currently, researchers use complex networks to model and study the performance of power grids. In fact, power grids can be modeled into a complex network by making use of ring network topology, with substations and transmission lines denoted as nodes and edges, respectively. In this paper, three protection schemes are proposed and their effectiveness in protecting the power network under high and low-load attacks is studied. The proposed schemes, namely, Cascaded Load Cut-off (CLC), Cascaded Load Overflow (CLO) and Adaptive-Cascaded Load Overflow (A-CLO), improve the robustness of the power grids, i.e., decrease the value of critical tolerance. Simulation results show that CLC and CLO protection schemes are more effective in improving the robustness of networks than the A-CLO protection scheme. However, the CLC protection scheme is effective only at the expense that certain percentage of the network will have no power supply. Thus, results show that the CLO protection scheme dominates the other protection schemes, CLC and A-CLO, in terms of the robustness of the network, improved with the precise amount of load cut-off determined.
Keywords:
Electric Power Grid, Cascading Failure, Protection Schemes, Networks

1. Introduction
Over the last decade, there were many power outages and cascading failure of electric power grids around the world due to equipment failures and natural disasters. The most recent major power outage took place in India leaving 670 million with no provision of electricity [1] . The daily lives of millions of people and economy of the country were unquestioningly affected with the long hours of power outage.
Power failures are more often caused by unstable voltage levels and frequencies [2] . The instability of frequency from generated voltage will cause asynchronization of generators, greatly reducing power generation and ultimately causing blackouts. Moreover, natural disasters are another factor that heavily impacts the overall stability of power grid as they may damage overhead transmission lines. Due to technological advancements, the reliance of power systems on internet communication has increased with the systems being connected to the control center through internet. These infrastructures could be vulnerable targets for terrorists as they can manipulate with the settings and trigger a power outage.
Cascading failures may happen when there are single or multiple faults in the power grid [3] . When a fault is found in the transmission lines or substations, the load is redistributed to remaining parts of the transmission network, which then leads to an overloading on the network. There are numerous researches revolving around cascading failure of power systems such as the recent blackout that occurred in India [1] .
Cascading failures greatly affect our lives and industries, and are commonly discovered in intricate communication and transportation networks [4] [5] . Though most failures occur and vanish insignificantly, there are still handfuls that give rise to avalanche mechanisms which can disrupt the entire network. When cascading failures happen on the internet, the traffic is rerouted to other routers to avoid the one that has malfunctioned. If these routers are not developed or designed to withstand the additional traffic, they will suffer from an avalanche of overloads. A significant drop will occur both in performance and speed of the connection [6] [7] . Large cascading failures also exist in social and economic systems [8] .
Another reason for cascading failure is the malfunctioning due to disturbance of components (transmission lines, power relays, circuit breakers, transformers, etc.). Such malfunctions may lead to the redistribution of power to the surrounding transmission lines or substations, which eventually creates overloading on these neighbors and can cause them to fail as well [9] . A similar incident associated with the power grid cascading failure took place in New Delhi, India and a large portion of northern India was left without power supply, affecting 670 million residents. This was one of the most fatal blackouts in the past decade.
Since there are many systems that are prone to cascading failure, this study will mainly focus on power systems and discuss more about the structure of power grids. An electrical power grid can be referred as a network which caters electricity source to the end user. It consists of three main elements as given below:
・ Power station, which generates power derived through fuel, fossil or non-combustible,
・ Power transmission line, which brings power from the plants to the substations,
・ Power distribution substation, which distributes the power to end users.
Electrical power is created at power stations and emitted across the network using transmission lines. These high voltage transmission lines are built either on top of towers or under ground between the transmission substations. Each time electricity is produced from a generating station, the transmission substation increases stepping up the voltage through the transformers. This creates a large amount of electrical power that can be distributed across a large area. On the other hand, a step down transformer at the distribution substations decreases the transmitted voltage. This reduced voltages and power is then consumed by users.
The power demand and supply correlation directly affects the steadiness of power grids. When there is a disruption in the power generation and a rise in demand (or load), the transmission line might get tripped. The power distributors play a vital role in ensuring that power supply relationship is balanced and well-maintained in order to prevent grid failures. The load demand across the whole power network varies throughout the day. In addition, load demand at different regions may differ due to different energy consumption behaviors of the consumers. Thus, it is important for the power generation companies to have a demand response to support the grid for eternally changing demand [10] . The reason behind the power generation companies never generating a constant amount of power is due to the additional cost it may incur when the power is not used by the consumer.
A lot of research work is done to model the cascading failures in power grids by adopting the theory of complex networks. The authors [11] studied the stability of power grid in North America in close consideration with the cause of cascade failures. The study involved a vulnerability test that measures the proportional relationship with the mean of the normalized number of generators supplying every distribution substation. The study has come to infer that the power grid is robust against many failures but is weak towards the removal of nodes with the highest degree.
In [12] , the cascade-based attack on complex networks was studied in which a capacity tolerance parameter was used for each node and assuming that all paired nodes exchanged an identical flow on the shortest path. They initiated the cascading failures by removing random target nodes with respect to the topological characteristics and load dispersion. It is then concluded that the power grid complex network is able to withstand the random failure of nodes with equal loads. In other means, this may cause a large cascading failure when a higher load node fails.
The authors in [13] studied the robustness of power grid systems by considering their interdependence and load propagation cascading failures. A mathematical model is developed to analyse the load propagation in a single network. The authors claim that, although the initial failure occurs in the power grid, the fraction of survivals in the power grid is always greater than that in a communication network. The authors in [14] also presented a model for interdependencies between power systems and communication networks, and to analyse the intricate impacts on cascading failures. The authors used the IEEE 39-bus system and China’s Guangdong 500-kV system as examples to study their proposed model. They have investigated the structural impacts of dispatching data networks on load shedding in case of different attacks on power grids.
The authors in [15] conducted a similar research on the US power grid complex network. The cascading failures were triggered by targeting the highest and lowest load nodes (transformer/substations) within the network. The authors also included a tunable variable, α, for the initial load. Their study concluded that for α ≤ 0.6, the network is more prone to cascading failures when attacking the lowest-load node instead of the highest-load node [12] . The authors in [16] also made attacks on the edge (transmission lines) and found the similar findings as before. However, such studies may not be relevant to other countries like Singapore. In Singapore, the transmission lines were built underground and it is occasional that the underground transmission lines will be broken due to natural disasters except earthquakes, which are rare in Singapore.
In [17] , additional work on the protection of the power networks is reported. The authors have suggested to fine tune the capacity of the overcapacity nodes to protect the network. Thereby, it can avoid the overload of the nodes (substations) and, as a consequence, the cascading failure can be avoided. However, this idea would not be feasible to implement in a real system, especially because the capacity of the transformers will be difficult to adjust in a short period. An approach [18] from the security point of view is proposed to examine the vulnerabilities of complex networks like power systems against cascading failure threats.
As the research work described above, most of the historical studies have mainly concentrated on the cascading failure modeling, cascade control and defense methodologies, or a fundamental characteristic of coupled networks with no attention on the load. There are few efforts however to examine the additional protection to the neighboring nodes from the of burden load, thereby increasing the performance of complex networks by allowing to better resist the cascading failures. This negligence is worth investigating as the neighboring nodes can help prevent the cascading failure, when they will be provided proper protection resources.
Considering the cascading effect of the overloaded nodes in a power grid, we propose three protection methods to improve the effect of preventing the cascading failure without changing the initial capacity of the nodes. The main idea of the three proposed protection strategies to improve the robustness of the power grid is to lower the initial loads of the neighbouring nodes of the overloaded/attacked node so that it can better support the load re-distribution in order to avoid further cascading failures.
2. Proposed Protection Schemes
The protection scheme proposed by author in [17] adjusts the capacity of the overloaded nodes. However, it is not a feasible method since adjusting the capacity requires manipulating the size of the transformers which could not be done in a short span of time [17] . In this study, we will propose three protection schemes, namely cascaded load cut-off (CLC), cascaded load overflow (CLO) and adaptive-cascaded load overflow (A-CLO) to improve the robustness of the power grid, i.e., decrease the value of critical tolerance [15] . The essence of the proposed protection schemes is to reduce the initial loads of the substations, which also means to reduce the power supply of the consumer. This could be done through supervisory control and data acquisition (SCADA) systems by activating the relays remotely to disconnect the loads [19] .
In Figure 1, the node under possible attack is node i and node j is node i’s neighbor node. In fact, the initial load, L, and maximum capacity, C, of a node is vital in deciding if the node is going to be overloaded. In general, if the initial load of the nodes is high, the additional loads from the broken nodes will cause the overloading effect on the neighbour nodes and cascading failures will persist. Similarly, if the capacity of the nodes is too low, it will cause the same effect. Referring to Figure 1, when node i is broken, it will redistribute its initial load, Li, to its neighbour nodes, e.g., node j. Then, node j checks and determines if its original load, Lj, plus the redistributed load, ΔLji, from node i is greater than its maximum capacity, Cj, such that ΔLji + Lj > Cj. If the neighbouring node j, exceeds the capacity, then it will be overloaded and broken as well. This redistribution will occur and propagate to other nodes until all loads are under themaximum capacity and no node is broken. The formulas to obtain Lj, Cj and ΔLji are presented in Section 3.
2.1. Cascaded Load Cut-off (CLC)
In this protection strategy, the initial load of the nodes that are connected to the overloaded node will be cut off partially so as to accommodate the additional load that is redistributed from the overloaded node. The new load of the neighbour nodes will then be reduced to (1 − δ)Lj, where δ is a number between 0 and 1 and it represents the percentage of the cut-off load. The value of δ is predetermined by the power grid company. The value of δLj will be equal to the amount of load that will be without any power supply. In that case, some consumers of the neighbor nodes are forced to have no power supply. After the initial load of the neighbours is cut-off, the broken node’s load will be redistributed and compared. Referring to Figure 1, in case node i is overloaded, the loads of neighbouring nodes, 1, 2, 3 and 4, will be reduced by δ before receiving the redistribution of additional load from the broken node, i.
2.2. Cascaded Load Overflow (CLO)
The CLO is a modified strategy of CLC. In CLC, a certain amount of initial load, δ Lj, is cut-off and there is no more power supply from the network. This cut-off might affect the consumers especially for industrial users since a power shortage leads to high losses for the companies.
In the CLO strategy, the cut-off load, δ Lj, from the neighbouring nodes, will be further redistributed to their connecting nodes. The further redistribution of this load will follow the redistribution model as detailed in the next section. This redistribution will allow the neighbours to operate without affecting the power supply of the existing consumers. The broken node’s load will be redistributed after CLO has gone through redistribution.
The illustration of how CLO works can be seen in Figure 1 as well. If node i fails, the initial load of node 1 to node 4 will be reduced to (1 − δ)(Lj) and their cut-off loads, δ Lj, will be further redistributed to their neighboring nodes. For example, the cut-off load, δ L4, of node 4 will be redistributed to nodes 5, 6 and 7. After this load overflow is done, the normal overload redistribution from node i will then be executed.
2.3. Adaptive Cascaded Load Overflow (A-CLO)
A-CLO is a protection strategy that adaptively determines the amount of cut-off load, δ Lj, based on the excess capacity of the nodes that are connected to the neighbours of the broken node. A-CLO is unlike the other two protection strategies, CLC and CLO, where δ is predetermined and fixed by the network. In A-CLO, the neighbour node, j, of the broken node, i, will first determine its cut-off load, Δγj, which is obtained based on
Figure 1. An illustration of a broken node, i, and the neighbouring loads cut-off.
average excess capacity of the nodes connecting to node j and is given by
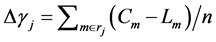 (1)
(1)
where,
・ rj is set of neighbouring nodes of node j,
・ Cm is maximum capacity of node m,
・ Lm is an initial load of node m,
・ n is number of nodes connecting to node j.
We limit Δγj ≤ 0.8 * Lj. Then, the amount of cut-off load, Δγj, of node j will be further re-distributed to its neighboring nodes before supporting the broken node.
In Figure 1, when node i fails, the network will calculate and decide the amount of required cut off load, Δγ4, of node 4 by averaging the excess capacity, C-L, of nodes 5 to 7. The initial load of node 4 will be reduced to L4-Δγ4. It means that node 4 will be able to support more of the normal load distribution from the overloaded node i. Then, Δγ4 will be distributed to its connecting nodes, 5 to 7, to ensure no disruption of power supply.
3. Simulation Model
3.1. Simulation Parameters
The power grid is modelled into a complex network graph G = (V, E), where V is the set of nodes (substations in the power grid), and E is the set of undirected and unweighted edges (transmission lines connecting two substations). The formulas for initial load, maximum load capacity and redistributed loadwill be introduced next and they are closely related to Wang’s cascade model [15] . They are defined as follows:
・ The initial load, Lx, of a node, x, depends on the degree (branch) of the node. The higher the degree (branch) is, the higher the initial load for that node can be. Lx is given by
 (2)
(2)
○ α is a tunable load factor which controls the strength of the initial load (load demand of the consumer).
○ kx is the sum of the degrees/branch of the neighboring nodes around node x.
○ rx is set of neighbouring nodes of node x.
・ Maximum load capacity, Cx, of a node x is given by
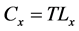 , (3)
, (3)
where, T is a fixed tolerance factor, T ≥ 1.
・ In case of a broken node, i, due to overloading, the load of the node i will be redistributed to its neighboring nodes proportionally. In order to calculate the potential amount of extra load which a neighboring node j receives after the redistribution of a node i. The formula for redistributed load, ΔLji, from node i to node j is given by
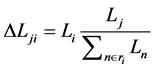 . (4)
. (4)
・ After load redistribution from node i to node j, node j will be broken if ΔLji + Lj > Cj. In that case, Steps 3 and 4 will be repeated such that the load of node j will be redistributed to its neighboring nodes.
・ When no more load is further redistributed, the avalanche size, CFattack, of cascading failure can be obtained as
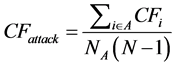 , (5)
, (5)
where, CFi is the number of broken nodes due to node i’s being overloaded, A and NA represents set and the number of nodes overloaded/attacked and Nis the total number of nodes in the network.
Next, the cascading failure model is conducted through the simulations by choosing a node for the attack. This enables comprehension of the role of each node in a power system network in case of a cascading failure. The effects of different attacks on power grid are analysed and the network robustness against these attacks are compared.
3.2. Attack Strategies
Two attack strategies are employed to compare the robustness of the networks.
・ High-load Attack (HLA): This strategy aims to attack on the nodes with the high-load. In this strategy, the nodes are selected in descending order of loads in the network. Only the single highest-load node will be attacked/overloaded at a time. After each simulation, the next higher-load node would be attacked/overloaded. The previously selected high-load node will be put back to its original state for the analysis of the cascading effect.
・ Low-load Attack (LLA): This strategy aims to attack on the nodes with the low-load. Adverse to the strategy with HLA, in this strategy, nodes are selected in ascending order of loads in the network. Only a single lowest-load node will be attacked/overloaded at a time. After each simulation, the next lower-load node would be attacked/overloaded. Similarly, the previously selected low-load node will be put back to its original state for the analysis of the cascading effect.
In order to quantify the robustness in the network, a critical threshold, Tc, is introduced. For T > Tc, the system is operating in normal condition with no cascading failure. That means CFattack = 0. On the other hand, for T < Tc, cascading failure exists in the network due to the failure of some nodes in the network. That means CFattack > 0. Thus, the critical threshold, Tc, is an important parameter for our study. A greater value of Tc means that the network is more prone to cascading failure as it needs a larger tolerance in order to prevent cascading failure from occurring.
3.3. Network Topologies
Most of the previous research work studied the USA’s real power grid while some other studies were based on a random network. In general, a simple network like power system can be modelled as an undirected and unweighted graph G = (V, E) where V is the set of nodes (substations in the power grid) and E is the set of undirected unweighted edges (transmission lines connecting two substations).
In order to create concrete outcomes for this study, we propose five different topologies. The characteristics of ring networks are adopted for all topologies in this study because of the stability it provides in the power distribution system. In the ring network, the substation is able to receive supply from both sides; the system will still be able to function properly through the supply received from either side [20] . In fact, ring network has been adopted in Singapore power grid. Three assumptions are made for ring networks used in this study. They are as follows:
・ Each of the “ring” consists of 5 lower voltage substations connected by low voltage transmission line.
・ Each medium voltage substation has 2 to 6 “rings” depending on the difference in topologies.
・ Each of the medium voltage substations are connected to one another via the medium voltage distribution line.
These topologies are created in an adjacency matrix form to represent them as a graph as shown in Figure 2, where it has 3 medium voltage substations with 2, 3 or 4 rings. Each ring has 5 low voltage substations. In total, there are 48 substations in Figure 2. The parameters used for five different topologies are shown in Table 1 in which each ring having 5 low voltage substations.
Table 1. The detail of the network topologies used in simulation.
Figure 2. An example of sub-network of the ring topology.
4. Simulation Results and Analysis
In this section, the performances of three proposed protection schemes, CLC, CLO and A-CLO, with different kinds of attacks are studied by computer simulation written in MatLab. All five network topologies are simulated to obtain each point shown in the figures. For each attack, HLA (LLA), under each network topology, five simulation runs will be done by selecting one high-load node (low-load node) in decreasing (increasing) order in each run. This means each point is obtained with an average of 25 simulation runs. These findings can be useful in designing the power grid system and in determining the tolerance for each substation in order to prevent the cascading failure.
4.1. Low-Load Attack with Protection Schemes
Table 2 shows the values of critical threshold, Tc, for different values of α and different protection schemes under LLA. In Table 2, it can be seen that the values of Tc for all protection schemes are smaller than the value of Tc for no protection scheme. This means that the proposed protection schemes are effective in mitigating the cascading failure during LLA. Comparing the effectiveness of the three protection schemes, it can be seen that for δ = 20% CLC and CLO give the lowest Tc in improving the network robustness. However, in CLC, each node connected to the overloaded node needs to sacrifice 20% of its initial load. That means some consumers may lose their power supply during this situation. On other hand, in CLO, the 20% of the initial load for each node connected to the overloaded node will be shared by its neighboring nodes. It means no node in the network will have power supply.
4.2. High-Load Attack with Protection Schemes
Table 3 shows the values of critical threshold, Tc, for different α with different protection schemes under HLA. It can be seen that all proposed protection schemes have lower Tc, except for CLO with δ = 20%, as compared to no protection scheme. That means that the proposed protection schemes are effective in mitigating the cascading failure during HLA.
It can be seen from Table 3 that CLO with high δ does not perform well with HLA. Theoretically, using CLO, the network is expected to be more robust against attacks for high δ because the neighbouring nodes of the overloaded node can take more extra load from the overloaded node. However, when there is too much load cut-off for CLO, i.e., δ = 20%, Tc increases. The reason is that since this 20% of initial load from each neighbouring node of the overloaded node will be redistributed to its neighbouring nodes, those neighbouring nodes can be easily overloaded, resulting in network failure. Then, it will create another overloaded node in other part of the network. This is due to the fact that CLO in essence redistributes the percentage of cut-off load from overloaded node’s neighbours. When the highest load node is broken, the neighbour nodes of this broken node will distribute their 20% initial loads to their neighbour nodes. After that, if any one of the neighbouring nodes is overloaded, it needs to further redistribute 20% of its initial load to its neighbours again. As an example in Figure 3, the neighbour nodes, 1 to 7, of the broken node, will redistribute 20% of their initial loads to their neighbour nodes. For node 5, it can only redistribute 20% of its initial load to node 8because node 8 is only one
Table 2. The critical tolerance of three protection schemes under LLA.
Table 3. The critical tolerance of the three protection schemes under HL.
Figure 3. Illustration of broken node with the highest load.
neighbour of node 5. Thus, node 8 will be easily overloaded because it will take all 20% of the initial load from node 5. As a result, the network failure possibly happens.
Figure 4 shows CF vs. T with different protection schemes for HLA at α = 0.6. In Figure 5, it can be seen that the percentage of failure nodes under CLO with δ = 20% in the network is less than 5%. It is still considered to be reasonably small as compared to other schemes. Whenever the network is failed, other schemes have almost 100% failure nodes. That means CLO with high δ does not cause too serious impact to the network.
4.3. Protection Schemes for Random Load Demand
The results in previous Sections assume that the tunable load parameter, α, is constant throughout the network. In this simulation, each node selects a value of α randomly for the range of 0.4 £ α £ 0.8 to make it more realistic. Since α is related to the consumer load demand, different nodes may have different requirements.
Figure 4. CF vs. T with protection schemes for HLA at α = 0.6.
Figure 5. Zoom in plot of CF vs. T.
From Table 4, the CLC and CLO have lower Tc for both attacks as compared to no protection scheme. However, A-CLO does not improve the Tc for HLA under variable α. The reason for the ineffectiveness of the A-CLO on HL is due to the dynamic load distribution of cascading failure model which was affected by the random tuneable load α. For A-CLO, the initial loads to be redistributed is based on average excess capacity of the nodes connecting to node neighbor nodes of the broken node as in Equation (1) which depends on the initial load of nodes. If α is different among nodes, it makes the difference between nodes’ initial loads very large. Thus, the cut-off load, Δγj, obtained in Equation (1) is not good enough and it will make some neighbor nodes to be overloaded easily.
4.4. Optimal δ for CLO
A shown in Table 3, CLO at δ = 20% has higher Tc than δ = 10%. So, it is important to determine the optimal δ to be reduced for redistribution. With δ = 20%, it means that all the neighboring nodes connected to the broken node will reduce their initial loads by 20% in order to support the additional load redistributed by the broken node. The 20% of the initial load of the neighboring nodes will then be redistributed further to their connecting nodes. Theoretically, higher δ allows the nodes connected to broken node to support more additional load from the broken node. Thus, Tc can be improved. However, the redistribution of the cut-off load needs to be considered. As δ increases, larger amount of these loads will be redistributed to their connecting nodes. If these connecting nodes do not have enough capacity to withstand, they will be overloaded and broken eventually.
Figure 6 shows the values of T with different δ at α = 1 for HLA and LLA. For LLA, Tc decreases with δ. However, for HLA, the Tc decreases with δ. Then, the Tc starts to increase after the optimal δ. So, there is an optimal δ for HLA. The optimal values of δ for different α for HLA are shown in Table 5. It can be seen that as α increases, the optimal δ increases as well. This is due to the higher capacity of the nodes as α increases.
Table 4. The values of Tc of the three protection schemes with random α.
Table 5. Optimal δ for HLA for each α.
Figure 6. Tolerance vs. initial load cut-off, δ, in %.
5. Conclusions
In order to study the methods to protect the power grid network through reduction of critical tolerance, Tc, three protections schemes are proposed in this paper. We have determined the effectiveness of the proposed schemes in protecting the network. For the low-load attack, all three protection schemes are effective in mitigating the cascading failure. However, during high-load attack, CLO protection scheme with a load cut-off of 20% performs worst with a high Tc. A further investigation finds that the load cut-off for the CLO scheme should not be too large as these loads will further redistribute to neighboring nodes and thus, those neighboring nodes might be overloaded as a consequence. This phenomenon induces us to find the optimal initial load cut-off and it is concluded that the optimal initial load cut-off is not fixed.
Accordingly, it can be concluded that CLC and CLO schemes are more effective in improving the robustness of the network than A-CLO protection scheme. However, CLC protection scheme is effective only at the expense of a certain percentage of networks having no power supply. Thus, CLO protection scheme dominates all the other protection schemes, CLC and A-CLO, as CLO can give a lower Tc with the right amount of load cut-off determined.
Cite this paper
Arun Kumar,Hnin Yu Shwe,Peter Han Joo Chong, (2016) Protection Strategies against Cascading Failure for Power Systems of Ring Network. Communications and Network,08,67-78. doi: 10.4236/cn.2016.82008
References
- 1. (2012) Selected Information about the July 31 Blackout in India Affecting the Northern and Eastern Regions. Power Systems Engineering Research Center (PSERC’12).
- 2. Dobson, I., Carreras, B.A., Lynch, V.E. and Newman, D.E. (2007) Complex Systems Analysis of Series of Blackouts: Cascading Failure, Critical Points, and Self-Organization. Chaos: An Interdisciplinary Journal of Nonlinear Science, 17, 1-13.
http://dx.doi.org/10.1063/1.2737822 - 3. Little, R.G. (2002) Controlling Cascading Failure: Understanding the Vulnerabilities of Interconnected Infrastructures. Journal of Urban Technology, 9, 109-123.
http://dx.doi.org/10.1080/106307302317379855 - 4. Dorogovtsev, S.N. and Mendes, J.F.F. (2003) Evolution of Networks: From Biological Nets to the Internet and WWW. Oxford University Press, Oxford.
- 5. Strogatz, S.H. (2001) Exploring Complex Networks. Nature, 410, 268-276.
http://dx.doi.org/10.1038/35065725 - 6. Jacobson, V. (1988) Congestion Avoidance and Control. ACM SIGCOMM Computer Communication Review, 18, 314-329.
http://dx.doi.org/10.1145/52325.52356 - 7. Guimera, R., Arenas, A., Diaz-Guilera, A. and Giralt, F. (2002) Dynamical Properties of Model Communication Networks. Physical Review, 66, 1-8.
- 8. Watts, D.J. (2002) A Simple Model of Global Cascades on Random Networks. Proceedings of the National Academy of Sciences of the United States of America, 99, 5766-5771.
http://dx.doi.org/10.1073/pnas.082090499 - 9. Kadloor, S. and Santhi, N. (2010) Understanding Cascading Failures in Power Grids. IEEE Transactions on Smart Grid, 1-12.
- 10. Johal, H., Anaparthi, K. and Black, J. (2012) Demand Response as a Strategy to Support Grid Operation in Different Time Scales. Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE’12), Raleigh, 15-20 September 2012, 1461-1467.
http://dx.doi.org/10.1109/ecce.2012.6342642 - 11. Réka Albert, I.A. and Nakarado, G.L. (2004) Structural Vulnerability of the North American Power Grid. Physical Review, 69, 1-4.
- 12. Motter, A.E. and Lai, Y.-C. (2002) Cascade-Based Attacks on Complex Networks. Physical Review, 66, 1-4.
- 13. Huang, Z., Wang, C., Zhu, T.Y. and Nayak, A. (2015) Cascading Failures in Smart Grid: Joint Effect of Load Propagation and Interdependence. IEEE Access, 3, 2520-2530.
http://dx.doi.org/10.1109/ACCESS.2015.2506503 - 14. Cai, Y., Cao, Y.J., Li, Y., Huang, T. and Zhou, B. (2016) Cascading Failure Analysis Considering Interaction Between Power Grids and Communication Networks. IEEE Transactions on Smart Grid, 7, 530-538.
http://dx.doi.org/10.1109/TSG.2015.2478888 - 15. Wang, J.-W. and Rong, L.-L. (2009) Cascade-Based Attack Vulnerability on the US Power Grid. Safety Science, 47, 1332-1336.
http://dx.doi.org/10.1016/j.ssci.2009.02.002 - 16. Wang, J.-W. and Rong, L.-L. (2011) Robustness of the Western United States Power Grid under Edge Attack Strategies due to Cascading Failures. Safety Science, 49, 807-812.
http://dx.doi.org/10.1016/j.ssci.2010.10.003 - 17. Wang, J. (2013) Robustness of Complex Networks with the Local Protection Strategy against Cascading Failures. Safety Science, 53, 219-225.
http://dx.doi.org/10.1016/j.ssci.2012.09.011 - 18. Yan, J., He, H.B. and Sun, Y. (2014) Integrated Security Analysis on Cascading Failure in Complex Networks. IEEE Transactions on Information Forensics and Security, 9, 451-463.
http://dx.doi.org/10.1109/TIFS.2014.2299404 - 19. Barnes, K., Johnson, B. and Nickelson, R. (2004) Introduction to SCADA Protection and Vulnerabilities. Idaho National Engineering and Environmental Laboratory, Bechtel BWXT Idaho, LLC, United States.
http://dx.doi.org/10.2172/911209 - 20. Yang, X.M. and Jiang, J.L. (2008) Study on Power Supply of Ring Network of 10KV Distribution Network. Proceedings of the China International Conference on Electricity Distribution (CICED’08), Guangzhou, 10-13 December 2008, 1-5.








