Communications and Network
Vol.3 No.4(2011), Article ID:8468,10 pages DOI:10.4236/cn.2011.34023
Application of Heuristic (1-Opt Local Search) and Metaheuristic (Ant Colony Optimization) Algorithms for Symbol Detection in MIMO Systems
1Electrical Engineering Department, National University of Sciences and Technology, Islamabad, Pakistan
2Military College of Signals, National University of Sciences and Technology, Islamabad, Pakistan
3Iqra University, Islamabad, Pakistan
E-mail: kiran.khurshid@yahoo.com
Received July 2, 2011; revised August 4, 2011; accepted August 15, 2011
Keywords: Spatial Multiplexing System, 1-Opt, ACO, Multi-Input Multi-Output Systems, Symbol Detection
Abstract
Heuristic and metaheuristic techniques are used for solving computationally hard optimization problems. Local search is a heuristic technique while Ant colony optimization (ACO), inspired by the ants’ foraging behavior, is one of the most recent metaheuristic technique. These techniques are used for solving optimization problems. Multiple-Input Multiple-Output (MIMO) detection problem is an NP-hard combinatorial optimization problem. We present heuristic and metaheuristic approaches for symbol detection in multi-input multi-output (MIMO) system. Since symbol detection is an NP-hard problem so ACO is particularly attractive as ACO algorithms are one of the most successful strands of swarm intelligence and are suitable for applications where low complexity and fast convergence is of absolute importance. Maximum Likelihood (ML) detector gives optimal results but it uses exhaustive search technique. We show that 1-Opt and ACO based detector can give near-optimal bit error rate (BER) at much lower complexity levels. Comparison of ACO with another nature inspired technique, Particle Swarm Optimization (PSO) is also discussed. The simulation results suggest that the proposed detectors give an acceptable performance complexity trade-off in comparison with ML and VBLAST detectors.
1. Introduction
One of the major impairment of the wireless communication channel is fading and the performance of radio channels is mainly governed by fading. Traditional mobile radio channel has always suffered from the detrimental effects of multipath fading but fortunately the use of multiple antennae at both ends of wireless channel helps mitigate the impairing effects of fading; MIMO wireless antenna systems provide an increase in capacity without the need for additional spectrum or power. The relevant information-theoretic analysis reveals that significant performance gains are achievable in wireless communication systems using a MIMO architecture employing multiple antennas [1].
This architecture is suitable for higher data rate multimedia communications [2].
In order to exploit all the benefits offered by the MIMO systems both the transmitter and the receiver need to be optimally designed. However, a problem encountered in the design of receivers for MIMO systems is the detection of data from noisy measurements of the transmitted signals. In realistic scenarios, due to noise, the receiver can make occasional errors. Therefore, designing a receiver which has the property that the probability of error is minimal is appealing, both from a practical and a theoretical point of view. But such designs tend to result in computationally complex receivers. We want computationally feasible receivers that give good performance.
Optimization problems are of high importance both for the industrial world as well as for the scientific world. MIMO detection problem is an “NP-hard” combinatorial optimization problem and solving this problem to optimality is computationally infeasible. In order to solve NP-hard problem for any non-trivial problem size, there can be three approaches: Approximation, probabilistic and heuristic approach. Approximate algorithms are those which quickly find a suboptimal solution which is within a certain range of the optimal one. Probabilistic algorithms are those which provably yield good average runtime behaviour for a given distribution of the problem instances. Heuristic algorithms work reasonably well on many cases, but for them there is no proof that it is always fast.
The local search heuristics iteratively search a better solution in the neighborhood of the current solution until no better solution exists and thus a local optimum is reached. The variable depth search (VDS) is known to be a generalization of the local search methods. The VDS was applied by Lin and Kernighan to the travelling salesman problem (TSP) and graph partitioning problem (GPP).
ACO, a meta-heuristic approach, is a popular branch of swarm intelligence. The goal of swarm intelligence is the design of intelligent multi-agent systems by taking inspiration from the collective behaviour of social insects such as ants, termites, bees, wasps, and other animal societies such as flocks of birds or fish schools. Examples of “swarm intelligent” algorithms other than ACO are those for clustering and data mining inspired by ants’ cemetery building behaviour [3,4], those for dynamic task allocation inspired by the behaviour of wasp colonies [5], and particle swarm optimization [6].
ACO was first introduced by Marco Dorigo and colleagues in the early 1990s [7,8]. The foraging behaviour of real ant colonies is exploited in artificial ant colonies for the search of approximate solutions to discrete optimization problems, to continuous optimization problems, and to important problems in telecommunications, such as routing and load balancing.
In this paper, we have merged the optimization techniques and the symbol detection problem. 1-Opt and ACO based algorithms are applied to NP-hard problem in the area of wireless communications.
Earlier, particle swarm optimization (PSO) has been successfully applied to the MIMO detection for the first time in [9].
The problem is to detect symbols from a composite signal, received at multiple receivers, transmitted from multiple transmitters. In this paper we discuss uncoded MIMO systems. Though coded MIMO schemes offer better performance than separate channel coding and modulation scheme by fully exploring the trade off between multiplexing and diversity [10], its hardware complexity can be significant, especially for wide band system with higher number of transmitter and receiver antennas. Also, it is easier to implement traditional channel coding schemes (Convolution code, Turbo code) for data rates of hundreds of Mbps.
Uncoded MIMO system, also called spatial multiplexing, is shown in Figure 1.
There are many MIMO detection technologies for spatial multiplexing [11]. These can be categorized as linear and non-linear detection methods. Zero-forcing (ZF) and Minimum Mean Squared Error (MMSE) are examples of linear detection method while Maximum Likelihood (ML) and Vertical Bell labs Layered Space Time (VBLAST) detectors [12,13] are two famous non-linear MIMO detection methods. Non-linear detectors give better performance but are computationally complex as compared to linear detectors.
We report ACO assisted MIMO detection algorithm with a reasonable performance complexity trade off and to the best of authors understanding this is first successful attempt to optimize MIMO detection using ACO meta-heuristic.
The remainder of this paper is organized as follows. In Section 2, the MIMO system model is introduced. Brief overview of existing detectors is given in Section 3. Fundamentals of 1-Opt and ACO are explained in Section 4. Proposed detection schemes are described in Section 5. Simulation parameters and results are discussed in Section 6. The computational complexity is calculated in Section 7. Concluding remarks can be found in Section 8.
2. Mimo System Model
2.1. Notation and Channel Model
A MIMO channel with Nt transmitters and Nr receivers is typically represented as a matrix H of dimension Nr × Nt, where each of the coefficients [H]i,j represents the transfer function from the jth transmitter to the ith receiver. We denote the signal or symbol transmitted from the jth transmitter xj. With this notation, the matrix model of the channel is
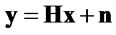 (1)
(1)
where n is a vector of additive noise, and y is an Nr × 1 complex received vector. H is a complex matrix representing the Rayleigh flat fading channel. Each coefficient hij shows the complex path gain between the jth transmits and ith receive antenna. Assuming the presence of a rich
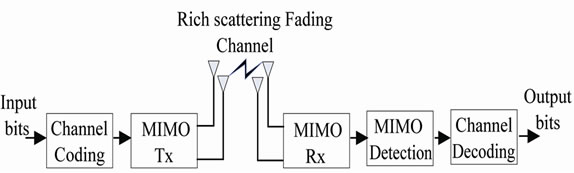
Figure 1. Spatial multiplexing system.
scattering environment, the columns of H are independent and entries hij are modelled as independent zero mean complex Gaussian random variables with unit variance. x is a Nt × 1 complex transmitted vector. n is an Nr × 1 complex noise vector whose components ni are modelled as zero mean independent complex Gaussian random variables with variance 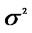 per real dimension.
per real dimension.
2.2. Problem Formulation
The optimum receiver that is capable of detecting the transmitted data vector x while minimizing the probability of making an erroneous decision, assuming equally likely uncoded transmit symbols, is the Maximum-Likelihood (ML) detector [14].
Assuming the additive noise n to be white and Gaussian, the ML detection problem can be expressed as the minimization of the squared Euclidean distance to a target vector y
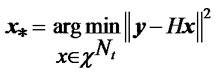 (2)
(2)
Optimal ML detection scheme needs to examine all 2bNt symbol combinations (b is the number of bits per symbol). It performs exhaustive search, i.e. the enumeration of all possible solutions and choosing the one that minimizes the objective function of (2).
A naive implementation of this search strategy results in a prohibitive complexity, as the number of candidate solutions increases exponentially with the problem size.
We present two approaches, 1-Opt and ACO algorithm assisted wide band spatial multiplexing systems symbol detector that views the MIMO symbol detection issue as a combinatorial optimization problem and try to approximate the near optimal solution iteratively.
3. Some Existing Mimo Detectors
3.1. Linear MIMO Detectors
Linear receivers are the class of receivers for which the symbol estimate 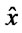 is given by a transformation of the received vector y of the form
is given by a transformation of the received vector y of the form
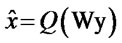
where W is a Weighting matrix that may depend on H and Q is a quantizer (also called slicer) that maps its argument to the nearest signal point in 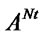 (using Euclidian distance). A is the modulation symbol and Nt is the total number of transmitters.
(using Euclidian distance). A is the modulation symbol and Nt is the total number of transmitters.
1) Zero-Forcing (ZF): ZF receiver is a low-complexity linear detection algorithm. The ZF algorithm attempts to null out the interference introduced from the matrix channel by directly inverting the channel with the weight matrix [15].
Zero-Forcing (ZF) outputs
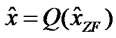
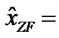 H†Y Where H† denotes the pseudo-inverse of H and
H†Y Where H† denotes the pseudo-inverse of H and 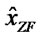 is rounded to the nearest integer in the constellation from which x is selected. The ZF notation comes from the fact that this receiver attempts to force the cross correlation between the estimation error e,
is rounded to the nearest integer in the constellation from which x is selected. The ZF notation comes from the fact that this receiver attempts to force the cross correlation between the estimation error e, 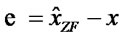 , and the transmit vector x to zero.
, and the transmit vector x to zero.
The ZF-receiver is a linear receiver in the sense that it behaves as a linear filter, separating the different data streams to perform independent decoding on each stream, hence eliminating multistream interference. The problem with this scheme is degraded performance due to the fact that the AWGN n loses the “whiteness” property; it becomes enhanced and correlated across the data streams. Moreover, the ZF-receiver provides only Nr − Nt + 1 diversity order out of a maximum possible Nr order diversity in a Nt × Nr MIMO system [1]. On the bright side, the ZF-receiver has a polynomial complexity.
2) Minimum Mean Squared Error (MMSE): A drawback of ZF is that nulling out the interference without considering the noise can boost up the noise power significantly, which in turn results in performance degradation. To solve this, MMSE minimizes the mean squared-error, i.e.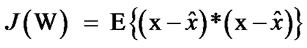 , with respect to W [16,17].
, with respect to W [16,17].
3.2. Non-Linear MIMO Detectors
1) VBLAST: VBLAST is the improvement of BLAST receiver. The detection algorithm associated with the BLAST architecture is the successive cancellation (SUC) algorithm. Rather than jointly decoding all of the t transmitted symbols, this nonlinear detector decodes the first transmitted symbol by satisfying the ZF or MMSE performance criterion while treating the rest of the data symbols as interference; then it cancels out its contribution to obtain a reduced order integer least-squares problem with t-1 unknowns. The process is repeated until all the symbols are detected. In general, this algorithm performs better than the ZF or MMSE receivers, but it suffers from error propagation; its performance quickly degrades if that first symbol was incorrectly decoded. A suggested improvement is the use of ordered successive cancellation (OSUC), an algorithm associated with the VBLAST architecture [18]. The main idea behind OSUC is that rather than selecting the symbols to be decoded in their natural order as in SUC, the symbols at the beginning of each decoding stage are ordered in terms of decreasing signal-to-interference noise ratio (SNR), and the symbol with the highest SNR is selected for decoding.
2) ML Detector: Maximum Likelihood detector is optimal but computationally very expansive. Since it uses exhaustive search technique, it is not practical to use ML in large MIMO systems.
4. Fundamentals of 1-OPT and ANT Colony Optimization (ACO)
Local search algorithms start from some initial solution and iteratively try to improve the current solution by searching, within a pre-specified neighborhood, for better solutions. A neighborhood structure is used to specify the solutions’ neighborhood. Local search algorithms have been observed to be efficient in practice. The assumption that local optima are easy to obtain has never been challenged.
1-opt local search is defined by the solutions that can be reached by changing a single element in the current solution. Their algorithms are often called k-opt local search. The basic concept is to search a portion of large (k-opt) neighborhood while keeping a reasonable amount of computation time.
ACO is an attractive technique that is very effective in solving optimization problems that have discrete and finite search space. Since the optimal MIMO detection problem involves a search process across the finite number of possible solutions, ACO is an ideal candidate to solve this problem.
4.1. Ants and Natural Optimization
ACO algorithms belong to the class of metaheuristics [19-21]. The term metaheuristic, first introduced in [22], derives from the composition of two Greek words. Heuristic derives from the verb heuriskein which means “to find”, while the suffix Meta means “beyond, in an upper level”.
Ants are social insects. They live in colonies and their behaviour is governed by the goal of colony survival rather than being focused on the survival of individuals. The behaviour that provided the inspiration for ACO is how ants can find shortest paths between food sources and their nest. When searching for food, ants initially explore the area surrounding their nest in a random manner. While moving, ants leave a chemical pheromone trail on the ground. Ants can smell pheromone. When choosing their way, they tend to choose, in probability, paths marked by strong pheromone concentrations. As soon as an ant finds a food source, it evaluates the quantity and the quality of the food and carries some of it back to the nest. During the return trip, the quantity of pheromone that an ant leaves on the ground may depend on the quantity and quality of the food. The pheromone trails guide other ants to the food source. It has been shown in [23] that the indirect communication between the ants via pheromone trails known as stigmergy enables them to find shortest paths between their nest and food sources.
4.2. ACO Metaheuristic
In analogy to the biological example, ACO is based on the indirect communication of a colony of artificial ants mediated by artificial pheromone trails An ant is a simple computational agent, which probabilistically builds a solution by iteratively adding solution components to partial solutions by taking into account 1) a priori available heuristic information on the problem instance being solved i.e. problem-specific greedy heuristic (desirability function), and 2) artificial pheromone trails which change dynamically at run-time to reflect the ants’ collective search experience [24].
ACO uses exploratory-exploitive approach. It is easy to see that, as the search progresses, deposited pheromone dominates ants’ selectivity, reducing the randomness of the algorithm. Therefore, ACO is an exploitive algorithm that seeks solutions using information gathered previously, and performs its search in the vicinity of good solutions. However, since the ant’s movements are stochastic, ACO is also an exploratory algorithm that samples a wide range of solutions in the solution space.
A flow chart depicting the structure of ACO algorithm is shown in Figure 2 (given at the end).
5. Proposed Mimo (1-Optzfml & ACO Based) Detectors
In 1-Opt local search ZF, the initial guess is taken from ZF. A ZF initial solution estimate is used to define the radius of search. Constellation points around the ZF solution are searched using 1-Opt local search. 1-opt local search is defined by the solutions that can be reached by changing a single element in the current solution. Function (2) is used to find out the minimum Euclidian distance. First y is computed and then a ML search around the neighborhood of y is performed. The bits of received symbol are changed to get the neighbors of the symbol. Each of the Nt symbol generates a neighbor list, then a joint ML search over reduced constellations is performed.
We have used Quadrature Phase Shift Keying (QPSK). In QPSK two data bits are mapped on a single modulation
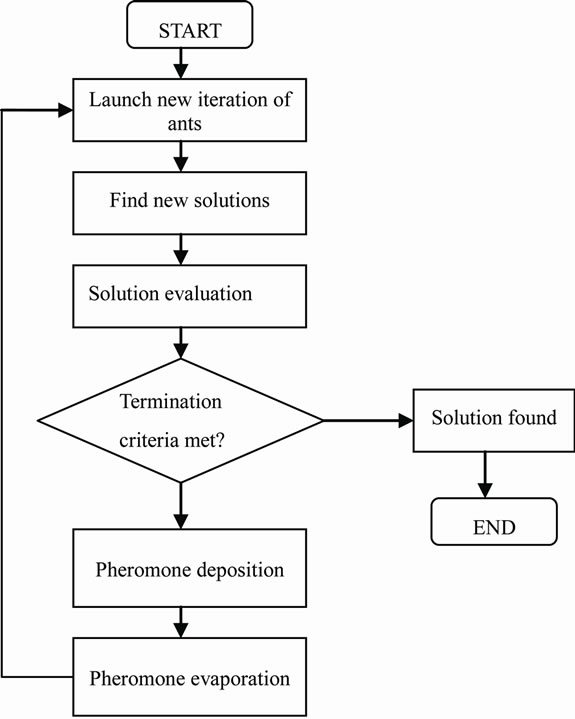
Figure 2. Flow chart depicting the structure of ACO algorithm.
symbol. 2 × 2 MIMO is considered so there are four neighbors in this case. ZF initial guess is taken and then four neighbors are generated using 1-Opt technique. ML search is performed to find Minimum Euclidean distance of y and its neighbors. Solution vector is the one with minimum Euclidean distance.
The major challenge in designing ACO based MIMO detector is the selection of effective fitness function which is problem dependent and perhaps is the only link between the real world problem and the optimization algorithms. The basic fitness function used by this optimization algorithm to converge to the optimal solution is (2).
The first stage in designing our ACO-based MIMO detector involves the selection of ACO parameters that fit the optimization problem. We define the solution vector to be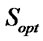 .
. 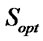 has length equal to Nt. In this algorithm we assume BPSK modulation scheme so each element of
has length equal to Nt. In this algorithm we assume BPSK modulation scheme so each element of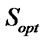 can take two values. A total of
can take two values. A total of 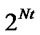 solutions are possible for BPSK scheme. Every ant builds a solution vector in each iteration. This building process is accomplished via Nt jumps inside a
solutions are possible for BPSK scheme. Every ant builds a solution vector in each iteration. This building process is accomplished via Nt jumps inside a 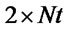 solution table, (soltable). Higher modulation schemes can also be used. If QPSK is used the table size would increase to
solution table, (soltable). Higher modulation schemes can also be used. If QPSK is used the table size would increase to 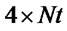 and possible solution would be
and possible solution would be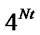 .
.
Choice of initial solution 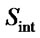 plays a vital role in the fast convergence of the optimization algorithm to a suitable solution. We therefore, make a start with the ZF or VBLAST input to the proposed detection algorithm. The first row of the soltable corresponds to the entries of initial solution,
plays a vital role in the fast convergence of the optimization algorithm to a suitable solution. We therefore, make a start with the ZF or VBLAST input to the proposed detection algorithm. The first row of the soltable corresponds to the entries of initial solution, 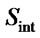 while the second row is the compliment of the first row i.e.
while the second row is the compliment of the first row i.e.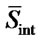 . If
. If 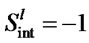 then
then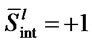 .
.
The ants move inside the soltable to find the optimal solution. In each jump, the ant selects (based on a desirability function and pheromone concentration) either the initial solution element or its complement. After each iteration, pheromone deposition and evaporation takes place. Any solution (out of the 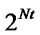 possible solutions) can be formed by selecting Nt elements from this table, one element from each column.
possible solutions) can be formed by selecting Nt elements from this table, one element from each column.
The ants start at 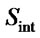 and move cyclically down the vector selecting the best element at each stage. Using the desirability function the ants decide whether to select element from
and move cyclically down the vector selecting the best element at each stage. Using the desirability function the ants decide whether to select element from 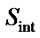 or
or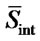 . Desirability function for initial position of ant starting at a particular instance j is defined as
. Desirability function for initial position of ant starting at a particular instance j is defined as
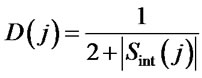 (3)
(3)
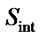 can either correspond to solution vector of ZF or V-BLAST.
can either correspond to solution vector of ZF or V-BLAST.
Equation (3) reflects the fact that when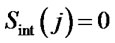 ,
, 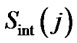 and
and 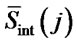 are equally likely to be chosen. As the ant moves along the elements of the solution vector, the desirability function at the (j + i)th stage can be redefined as follows:
are equally likely to be chosen. As the ant moves along the elements of the solution vector, the desirability function at the (j + i)th stage can be redefined as follows:
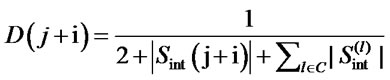 (4)
(4)
where C is a set of positions where the ant had previously selected 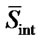 element values. The desirability function ensures that if at the jth position ant selects element from
element values. The desirability function ensures that if at the jth position ant selects element from 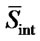 then at the (j+i)th position probability of selecting another element from
then at the (j+i)th position probability of selecting another element from 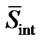 decreases. The purpose of such desirability function is that ant should not deviate significantly from initial solution.
decreases. The purpose of such desirability function is that ant should not deviate significantly from initial solution.
Pheromone deposition is also done in a 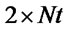 table. Each entry of first row of pheromone table corresponds to the entry of
table. Each entry of first row of pheromone table corresponds to the entry of 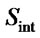 while second row entries correspond to
while second row entries correspond to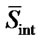 . Initially all the entries in the table are unity i.e.; equal amount of pheromone is deposited. In our algorithm if an ant produces a good solution only then it is allowed to deposit pheromone. Good solution is determined from the fitness function. Deposition and evaporation rate are inversely proportional to the number of iterations.
. Initially all the entries in the table are unity i.e.; equal amount of pheromone is deposited. In our algorithm if an ant produces a good solution only then it is allowed to deposit pheromone. Good solution is determined from the fitness function. Deposition and evaporation rate are inversely proportional to the number of iterations.
The proposed detection algorithm is summarized below
Step 1. Take the output of ZF or VBLAST as initial input to algorithm instead of keeping random values.
Step 2. Create a 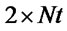 soltable, whose first row contains elements of
soltable, whose first row contains elements of 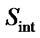 and second row
and second row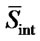 .
.
Step 3. Create a 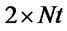 pheromone table, PT(m,n) = 1
pheromone table, PT(m,n) = 1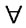 , m,n = 1 (initialization).
, m,n = 1 (initialization).
Step 4. Decide the starting position of ants i.e.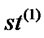 ,
, 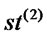 ,
, ,
,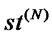 .
.
Step 6.
For iteration 1: itr{
for move = 0: Nt − 1{
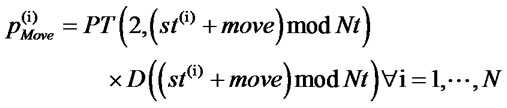
This is the probability with which ant i selects 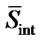 elements. It is evaluated for all ants.
elements. It is evaluated for all ants.
Selected elements and the index of the selected locations in PT are stored in two separate arrays, sol and Tr. “sol” is later used for checking whether the result is good or not while Tr constitutes the trail for ant.
}
Step 7. If 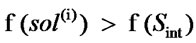
Step 7.1. Pheromones are deposited:
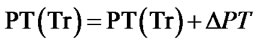
Change in pheromone table:
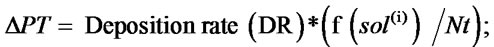
Step 8. Evaporation of pheromones:
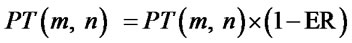
ER= evaporation rate.}
In the pheromone table, the trail with the highest pheromone concentration and its corresponding values from  and
and 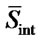 provide the final solution Sopt.
provide the final solution Sopt.
6. Simulation Parameters and Results
Aim of the proposed 1-Opt ZFML and ACO based MIMO detector is to lower the complexity level as much as possible, therefore the parameters are selected accordingly.
In ACO based MIMO detector we have used only one ant i.e., no. of ant, N = 1, number of iterations, itr are MIMO system dependant. i.e. 4 iterations if Nt = 4. DR = 5/itr, ER = 9/itr. We have considered 3 × 3 and 4 × 4 (Nt × Nr ) MIMO systems.
Figures (shown at the end) present the bit error rate (BER) versus Eb/No (SNR) performance of proposed detectors.
Figure 3 presents the BER versus Eb/No performance of proposed ACO based MIMO detector compared with ML and VBLAST detectors for 3 × 3. At 10–3 BER, the proposed ACO-VBLAST algorithm (with VBLAST as initial guess) result in 5-dB enhanced performance as compared to VBLAST while ACO-ZF algorithm (with ZF as initial guess), result in 8 dB gain compared to ZF.
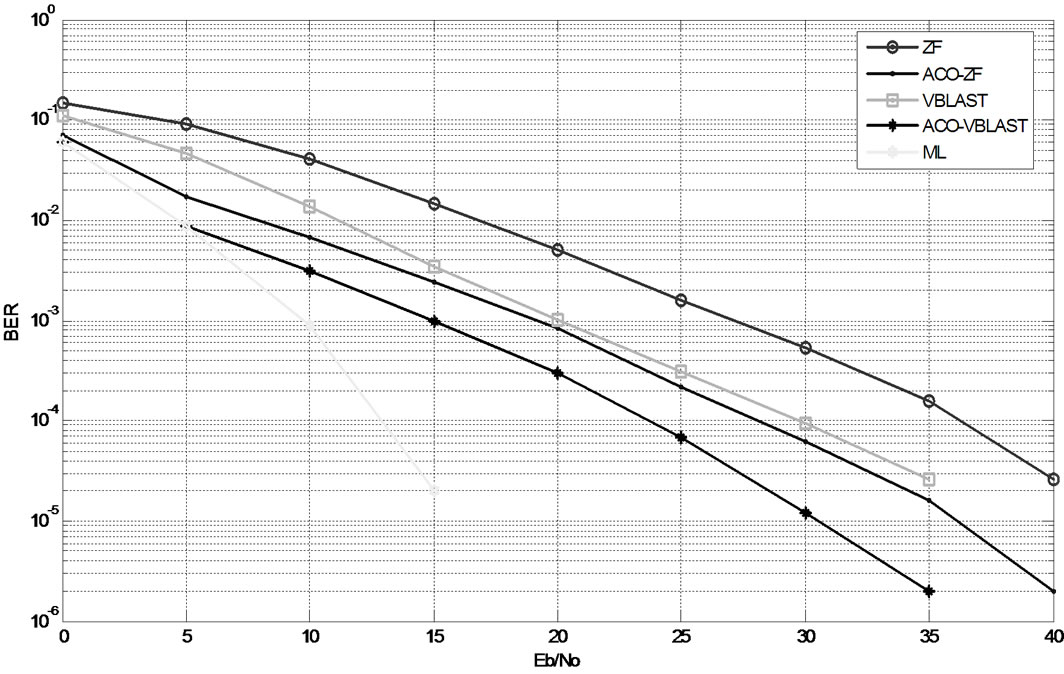
Figure 3. Detectors for 3 × 3 MIMO system.
Figure 4 presents the BER versus Eb/No performance of proposed ACO based MIMO detector compared with ML and VBLAST detectors for 4 × 4. At 10–3 BER, the proposed ACO-VBLAST algorithm result in 5-dB enhanced performance as compared to VBLAST while ACO-ZF algorithm result in 7-dB gain compared to ZF.
Figure 5 presents the BER versus Eb/No performance of proposed 1-Opt ZFML detector compared with the VBLAST detector. At 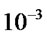 the 1-Opt ZFML gives 6 dB enhanced performance and complexity is also reduced by 8% as compared to VBLAST.
the 1-Opt ZFML gives 6 dB enhanced performance and complexity is also reduced by 8% as compared to VBLAST.
Figure 6 shows the comparison between ACO and PSO techniques for 4 × 4 MIMO system. Initial guess is taken from VBLAST and BPSK modulation scheme is
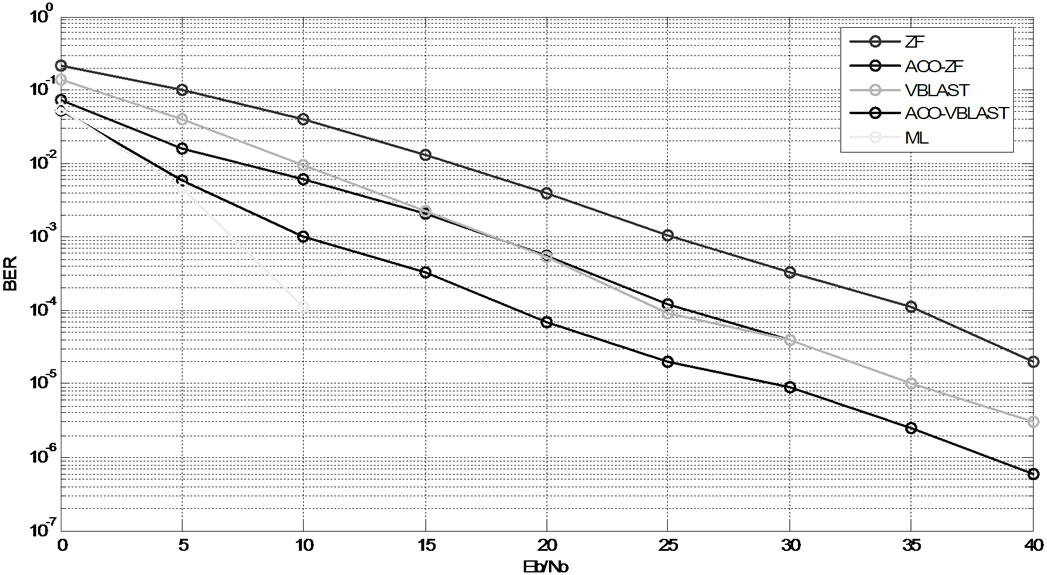
Figure 4. Detectors for 4 × 4 MIMO system.
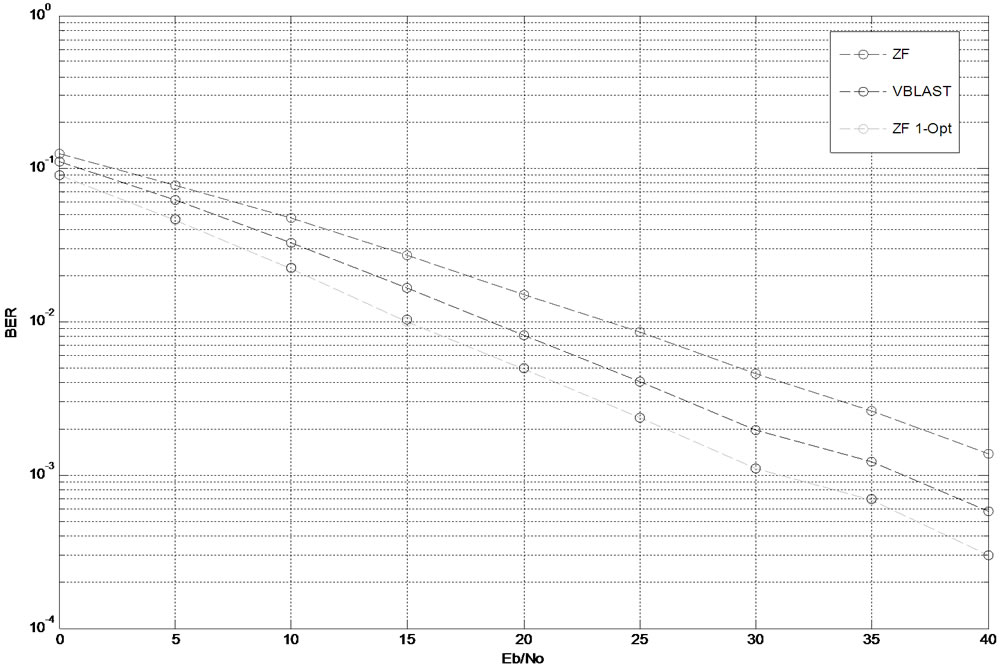
Figure 5. Comparison of 1-Opt ZFML detector with VBLAST.
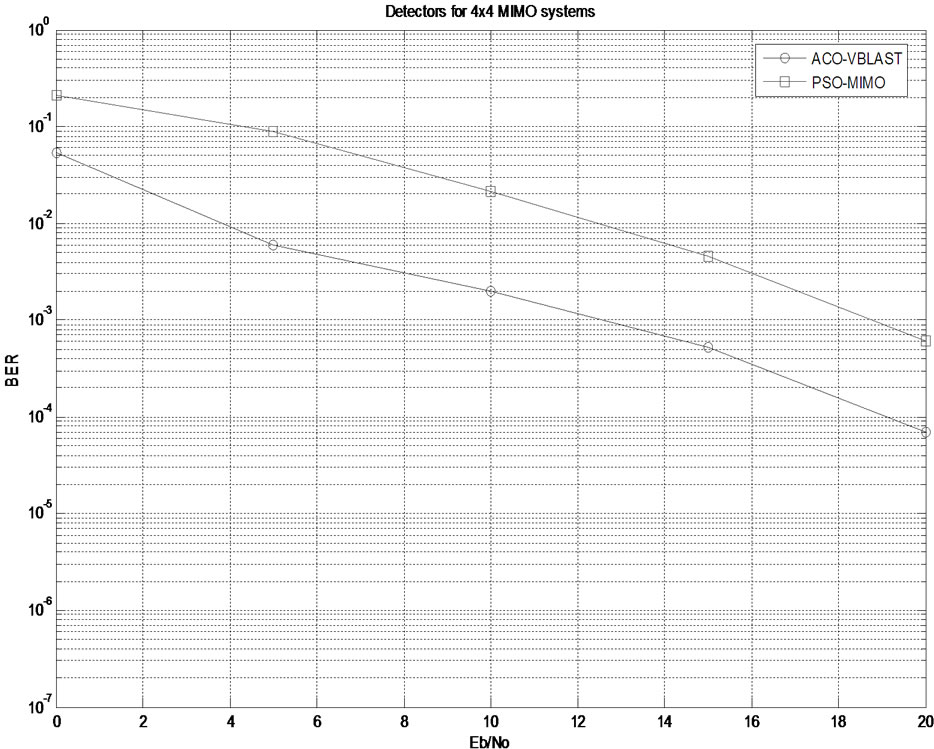
Figure 6. ACO and PSO detectors.
used in both the cases. The parameters for PSO [17] are Np = 4, Nitr = 2, μvel = 2. At 10–3 BER ACO gives 6 dB improved performance.
7. Computational Complexity
Now we examine the computational complexity of the reported ACO and 1-Opt ZFML MIMO detectors and compare it with ML and VBLAST detectors. The computation complexity of ML and VBLAST has been calculated in [25].
The computational complexity is computed in terms of the Nt, Nr and the constellation size M.
Computational complexity of ML is Nr (Nt+1) MNt while complexity of VBAST is
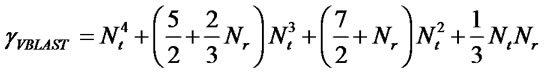
In case of ZF, the pseudo-inverse of matrix (HHH)–1 HH takes 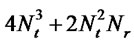 multiplications [9].
multiplications [9].
Complexity of ZF is
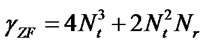
Complexity of PSO is [9]
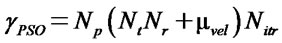
Complexity of proposed detector as seen from algorithm is
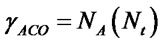
Pheromone update requires μp additional multiplications per iteration
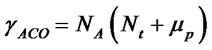
This procedure is repeated Nitr times to give the nearoptimal BER performance
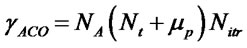
The proposed detector takes initial solution as ZF or VBLAST detectors’ output therefore, it is added to the complexity of ACO algorithm i.e. 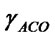 to get the resultant complexity of ACO based MIMO detector. It can be seen that ZF-ACO for 3 × 3 MIMO system gives a bit better performance than VBLAST at a reduced complexity level of 28% while ACO-VBLAST gives better performance than VBLAST at a cost of 9% increase in complexity. For 4 × 4 system ZF-ACO has 42% less complexity than VBLAST. While ACO-VBLAST gives better performance than VBLAST at a cost of around 4% increase in complexity level.
to get the resultant complexity of ACO based MIMO detector. It can be seen that ZF-ACO for 3 × 3 MIMO system gives a bit better performance than VBLAST at a reduced complexity level of 28% while ACO-VBLAST gives better performance than VBLAST at a cost of 9% increase in complexity. For 4 × 4 system ZF-ACO has 42% less complexity than VBLAST. While ACO-VBLAST gives better performance than VBLAST at a cost of around 4% increase in complexity level.
For 4 × 4 system shown in Figure 6 complexity of ACO based detector is 29% less than PSO based detector.
In case of 1-Opt ZFML the computational complexity is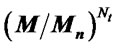 . Where Mn is the neighbors list. So the total complexity of 1-Opt
. Where Mn is the neighbors list. So the total complexity of 1-Opt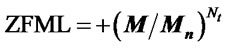 .
.
Compared to ML that performs a coarse search over the complete search space the 1-Opt ZFML used a reduced constellation.
8. Conclusions
In this paper, 1-Opt and Any Colony Optimization assisted symbol detection in a spatial multiplexing system is reported. It has been shown that the metaheuristics and heuristics can be applied to optimize the symbol detection problem. The resistance to being trapped in local minima, convergence to reasonable solution in fewer iterations and exploratory-exploitive search approach makes ACO a suitable candidate for real-time wireless communications systems. 1-Opt and ACO based MIMO detectors use a simple model and have lesser implementation complexity. For larger number of antennas and higher modulation schemes the proposed detectors are expected to give near optimal results with much lower complexity level as compared to the ML detector and VBLAST detectors.
9. References
[1] A. Paulraj, R. Nabar and D. Gore, “Intoduction to SpaceTime Wireless Communications,” Cambridge University Press, New York, 2003.
[2] S. Aon Mujtaba, “TGn Sync Proposal Technical Specification,” 2005. http://www.tgnsync.org/techdocs/11-04-0889-06-000n-tgnsyncproposal-technical-specification.doc
[3] G. J. Foschini and M. J. Gans, “On Limits of Wireless Communications in a Fading Environment When Using Multiple Antennas,” Wireless Personal Communications, Vol. 6, No. 3, 1998, pp. 311-335. doi:10.1023/A:1008889222784
[4] E. Lumer and B. Faieta, “Diversity and Adaptation in Populations of Clustering Ants,” In: J. A. Meyer and S. W. Wilson, Eds., Proceedings of the Third International Conference on Simulation of Adaptive Behavior: From Animals to Animats, Vol. 3, MIT Press, Cambridge, 1994, pp. 501-508.
[5] M. Campos, E. Bonabeau, G. Theraulaz and J.-L. Deneubourg, “Dynamic Scheduling and Division of Labor in Social Insects,” Adapt Behavior, Vol. 8, No. 3, 2000, pp. 83-96. doi:10.1177/105971230000800201
[6] J. Kennedy and R. C. Eberhart, “Particle Swarm Optimization,” Proceedings of the 1995 IEEE International Conference on Neural Networks, Vol. 4, IEEE Press, Piscataway, 1995, pp. 1942-1948. doi:10.1109/ICNN.1995.488968
[7] M. Dorigo, V. Maniezzo and A. Colorni, “Positive Feedback as a Search Strategy,” Technical Report 91-016, Dipartimento di Elettronica, Politecnico di Milano, 1991.
[8] H. Bolcskei, D. Gesbert and C. Papadias, “Space-Time Wireless Systems: From Array Processing to MIMO Communications,” Cambridge University Press, New York, 2005.
[9] A. A. Khan, M. Naeem and S. I. Shah, “A Particle Swarm Algorithm for Symbols Detection in Wideband Spatial Multiplexing Systems,” GECCO-07, 2007.
[10] L. Zheng and D. Tse, “Diversity and Multiplexing: A Fundamental Tradeoff in Multiple Antenna Channels,” IEEE Transaction on Information Theory, Vol. 49, No. 5, May 2003, pp. 1073-1096. doi:10.1109/TIT.2003.810646
[11] A. Goldsmith, S. A. Jafar, N. Jindal and S. Vishwanath, “Capacity Limits of MIMO Channels,” IEEE Journal on Selected Areas in Communications, Vol. 20, No. 5, June 2003.
[12] G. J. Foschini, “Layered Space-Time Architecture for Wireless Communication in a Fading Environment When Using Multiple Antennas,” Bell Labs Technical Journal, Vol. 1, No. 2, 1996, pp. 41-59. doi:10.1002/bltj.2015
[13] F. Glover and G. Kochenberger, “Handbook of Metaheuristics,” Kluwer Academic, Norwell, 2002.
[14] S. Verdu, “Multiuser Detection,” Cambridge University Press, New York, 1998.
[15] M. Dorigo, V. Maniezzo and A. Colorni, “Ant System: Optimization by a Colony of Cooperating Agents,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 26, No. 1, 1996, pp. 29-41. doi:10.1109/3477.484436
[16] S. Haykin, “Adaptive Filter Theory,” 3rd Edition, Prentice-Hall, Upper Saddle River, 1996.
[17] A. Sayed, “Fundamentals of Adaptive Filtering,” WileyIEEE Press, Piscataway, 2003.
[18] V. Tarokh, H. Jafarkhani and A. R. Calderbank, “SpaceTime Block Codes for Orthogonal Designs,” IEEE Transactions on Information Theory, vol. 45, No. 5, 1996, pp. 1456-1466. doi:10.1109/18.771146
[19] C. Blum and A. Roli, “Metaheuristics in Combinatorial Optimization: Overview and Conceptual Comparison,” ACM Computing Surveys, Vol. 35, No. 3, 2003, pp. 268- 308. doi:10.1145/937503.937505
[20] J. Handl, J. Knowles and M. Dorigo, “Ant-Based Clustering and Topographic Mapping,” Artificial Life, Vol. 12, No. 1, 2006, pp. 35-62. doi:10.1162/106454606775186400
[21] H. H. Hoos and T. Stützle, “Stochastic Local Search: Foundations and Applications,” Elsevier, Amsterdam, 2004.
[22] F. Glover, “Future Paths for Integer Programming and Links to Artificial Intelligence,” Computers & Operations Research, Vol. 13, No. 5, 1986, pp. 533-549. doi:10.1016/0305-0548(86)90048-1
[23] J. L. Deneubourg, S. Aron, S. Goss and J. M. Pasteels, “The Self-Organizing Exploratory Pattern of the Argentine Ant,” Journal of Insect Behavior, Vol. 3, No. 2, 1990, pp. 159-168. doi:10.1007/BF01417909
[24] M. Dorigo and T. Stutzle, “Ant Colony Optimization,” MIT Press, Cambridge, 2004.
[25] G. H. Golub and C. F. V. Loan, “Matrix Computations,” 3rd Edition, John Hopkins University Press, Baltimore, 1996.

