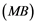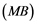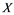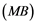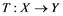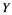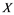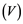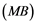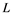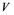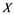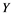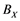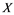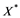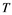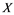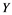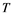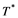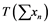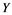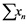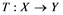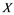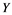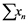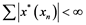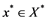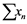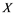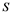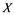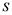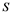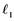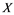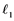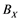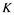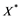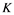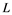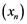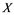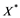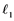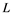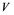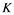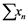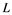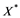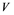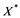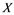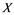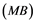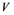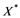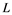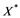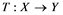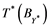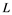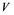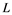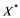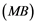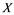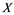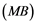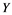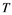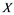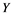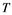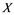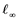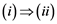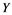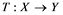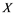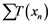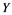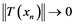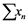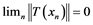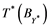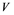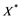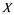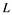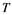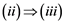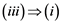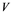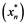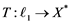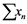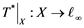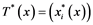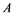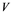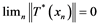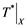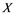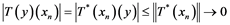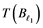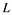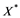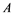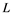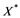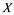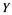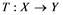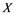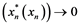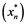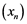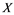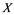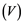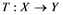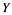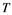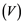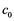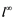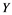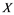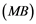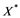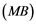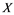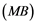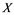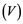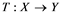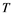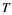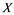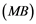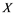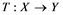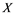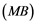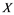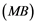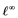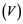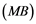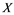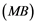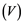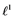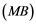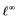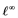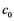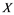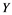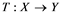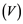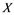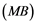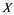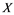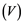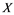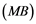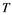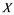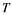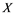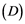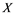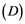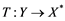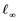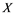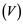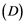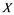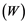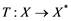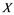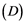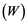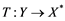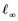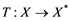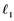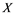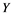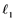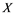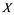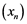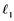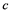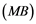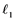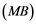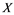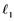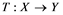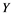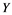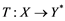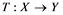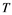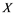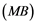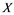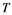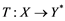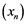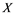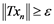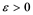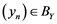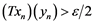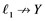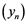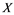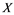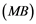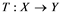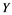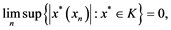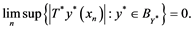Advances in Pure Mathematics
Vol.06 No.13(2016), Article ID:72770,6 pages
10.4236/apm.2016.613072
Space of Operators and Property 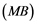
Manijeh Esfahani Bahreini
Department of Mathematics, Khansar Faculty of Mathematics and Computer Sciences, Khansar, Iran

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 12, 2016; Accepted: December 12, 2016; Published: December 15, 2016
ABSTRACT
In this paper, a new class of Banach spaces, termed as Banach spaces with property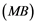 , will be introduced. It is stated that a space
, will be introduced. It is stated that a space  has property
has property  if every
if every 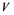 -subset of
-subset of 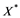 is an
is an 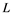 -subset of
-subset of . We describe those spaces which have property
. We describe those spaces which have property . Also, we show that if a Banach space
. Also, we show that if a Banach space 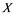 has property
has property 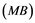 and Banach space
and Banach space  does not contain
does not contain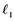 , then every operator
, then every operator 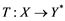 is completely continuous.
is completely continuous.
Keywords:
 -Sets,
-Sets,  -Sets, Completely Continuous Operators, Unconditionally Converging Operators
-Sets, Completely Continuous Operators, Unconditionally Converging Operators

1. Introduction
In 1992, Saab and Smith [1] studied Banach spaces with the property that every un- conditionally converging operator from such a space to an arbitrary Banach space is weakly completely continuous. It is well known that every completely continuous operator is an unconditionally converging operator. In this paper, the converse of this fact by using some localized properties, e.g.,  -sets,
-sets,  -sets will be studied.
-sets will be studied.
First, the property ![]() for Banach spaces is presented, then spaces which have property
for Banach spaces is presented, then spaces which have property ![]() are considered. Next, it is demonstrated that
are considered. Next, it is demonstrated that ![]() has property
has property ![]() if and only if every unconditionally converging operator
if and only if every unconditionally converging operator ![]() is completely continuous, for every Banach space
is completely continuous, for every Banach space![]() .
.
In [2] , it has shown that a Banach space ![]() has the Reciprocal Dunford-Pettis property whenever it has property
has the Reciprocal Dunford-Pettis property whenever it has property ![]() but the converse is false. We investigate under what conditions this implication could be reversed.
but the converse is false. We investigate under what conditions this implication could be reversed.
Also, it will verified that property ![]() implies the Dunford-Pettis property. In addition, we show that a Banach space with property
implies the Dunford-Pettis property. In addition, we show that a Banach space with property ![]() and the Dunford-Pettis property, as well has the property
and the Dunford-Pettis property, as well has the property![]() .
.
The notions of a relatively compact sets, ![]() -sets,
-sets, ![]() -sets have a significant role in this study.
-sets have a significant role in this study.
Definitions and Notation
In this article, real Banach spaces will be symbolized by ![]() and
and![]() , the unit ball of
, the unit ball of ![]() will be denoted by
will be denoted by![]() , and the continuous linear dual of
, and the continuous linear dual of ![]() will be denoted by
will be denoted by![]() . A continuous and linear map
. A continuous and linear map ![]() from
from ![]() to
to ![]() is called an operator, and the adjoint of
is called an operator, and the adjoint of ![]() is denoted by
is denoted by![]() . Also
. Also ![]() will stand for the set of all operators .
will stand for the set of all operators .
If ![]() is an operator from
is an operator from ![]() to
to ![]() and
and ![]() is an unconditionally con- vergent series in
is an unconditionally con- vergent series in ![]() whenever the series
whenever the series ![]() in
in ![]() is weakly unconditionally converging, then
is weakly unconditionally converging, then ![]() is called an unconditionally converging operator. A completely continuous operator is an operator
is called an unconditionally converging operator. A completely continuous operator is an operator ![]() which takes weakly null sequences in
which takes weakly null sequences in ![]() into norm convergent sequences in
into norm convergent sequences in![]() .
.
Recall that a series ![]() is weakly unconditionally converging if and only if
is weakly unconditionally converging if and only if ![]() for each
for each ![]() and the series
and the series ![]() is unconditionally converging if and only if every rearrangment converges in the norm topology of
is unconditionally converging if and only if every rearrangment converges in the norm topology of![]() .
.
Suppose ![]() is a bounded set in
is a bounded set in![]() , then it is stated that
, then it is stated that ![]() is weakly precompact if every single sequence from
is weakly precompact if every single sequence from ![]() includes a weakly Cauchy subsequence. Rosentlal’s
includes a weakly Cauchy subsequence. Rosentlal’s ![]() Theorem states that “A Banach space
Theorem states that “A Banach space ![]() does not contain copies of
does not contain copies of ![]() if and only if
if and only if ![]() is a weakly precompact set in
is a weakly precompact set in![]() .”
.”
The reader is referred to Diestel [3] or Dunford-Schwartz [4] for undefined notation and terminology.
2. Main Results
Let ![]() be a bounded set in
be a bounded set in![]() , then
, then ![]() is said to be an
is said to be an ![]() -set, if for all weakly null sequence
-set, if for all weakly null sequence ![]() in
in ![]() we have the following ,
we have the following ,
![]()
e.g., see [5] [6] [7] . Moreover, any ![]() -subset of
-subset of ![]() is relatively compact if and only if
is relatively compact if and only if ![]() does not embed in
does not embed in ![]() [5] [6] .
[5] [6] .
Closely related to the notion of ![]() -set is the idea of a
-set is the idea of a ![]() -set. Let
-set. Let ![]() be a bounded set in
be a bounded set in![]() , then
, then ![]() is called a
is called a ![]() -set, if for all weakly unconditionally converging series
-set, if for all weakly unconditionally converging series ![]() in
in![]() , we have the following
, we have the following
![]()
It can easily be derived directly from the definitions that every ![]() -subset of
-subset of ![]() is a
is a ![]() -subset of
-subset of![]() . Next, equivalent characterizations of Banach spaces such that the converse statement holds are defined.
. Next, equivalent characterizations of Banach spaces such that the converse statement holds are defined.
Initially, new property for Banach spaces will be introduced.
Definition 2.1. Let ![]() be a Banach space. Then we say that
be a Banach space. Then we say that ![]() has property
has property ![]() if each
if each ![]() -set in
-set in ![]() is also an
is also an ![]() -set in
-set in![]() .
.
Theorem 3.1 (ii) in [2] , plays a consistent and vital position in this research. It states that; A necessary and sufficient condition for an operator ![]() to be completely continuous is that
to be completely continuous is that ![]() is an
is an ![]() -subset of
-subset of![]() .
.
In the following, necessery and sufficient condition are given that every ![]() -subset of
-subset of ![]() is an
is an ![]() -subset of
-subset of![]() .
.
Now, the main theorem, which establishes Banach spaces with property ![]() will be determined as the resulting.
will be determined as the resulting.
Theorem 2.2. The following statements are equivalent about a Banach space![]() .
.
(i) ![]() has property
has property![]() .
.
(ii) Let ![]() be any Banach space, then an operator
be any Banach space, then an operator ![]() from
from ![]() to
to ![]() is completely continuous whenever
is completely continuous whenever ![]() is unconditionally converging.
is unconditionally converging.
(iii) If an operator ![]() from
from ![]() to
to ![]() is unconditionally converging, then it is also completely continuous.
is unconditionally converging, then it is also completely continuous.
Proof. ![]() Assume that
Assume that ![]() is a Banach space and operator
is a Banach space and operator ![]() is unconditionally converging. Now let the series
is unconditionally converging. Now let the series ![]() in
in ![]() be weakly unconditionally converging. Thus
be weakly unconditionally converging. Thus ![]() is an unconditionally converging in
is an unconditionally converging in ![]() and
and![]() . Hence for each weakly unconditionally converging series
. Hence for each weakly unconditionally converging series ![]() in X,
in X, ![]() , and thus we have the following,
, and thus we have the following,
![]()
This follows that ![]() is a
is a ![]() -set in
-set in![]() , and as
, and as ![]() has property
has property![]() , then it is also an
, then it is also an ![]() -set in
-set in![]() . Therefore the operator
. Therefore the operator ![]() is completely continuous [2] .
is completely continuous [2] .
![]() It is obvious.
It is obvious.
![]() Assume that
Assume that ![]() is a
is a ![]() -set in
-set in ![]() and let
and let ![]() be some sequence in A. Let us define
be some sequence in A. Let us define ![]() by
by ![]() and suppose that the series
and suppose that the series ![]() is weakly unconditionally converging in X. See that
is weakly unconditionally converging in X. See that![]() , and
, and![]() . As
. As ![]() is a
is a ![]() -set in, we have the following,
-set in, we have the following,
![]()
So![]() , which implies that the operator
, which implies that the operator ![]() is unconditionally converging. Finally, by assumption we conclude that
is unconditionally converging. Finally, by assumption we conclude that ![]() is a completely continuous operator. Now assume
is a completely continuous operator. Now assume ![]() is a weakly null sequence in
is a weakly null sequence in ![]() and
and![]() . Then
. Then![]() . Hence
. Hence ![]() is an
is an ![]() -set in
-set in ![]() which follows that
which follows that ![]() is also an
is also an ![]() -set in
-set in![]() . Therefore
. Therefore ![]() has property
has property ![]() and the proof is complete.
and the proof is complete. ![]()
Remembrance that if for every Banach space![]() , each operator
, each operator ![]() is completely continuous whenever
is completely continuous whenever ![]() is weakly compact operator, then
is weakly compact operator, then ![]() is said to have the Dunford-Pettis property. Equivalently,
is said to have the Dunford-Pettis property. Equivalently, ![]() has Dunford-Pettis property if and only if
has Dunford-Pettis property if and only if ![]() whenever
whenever ![]() is weakly null in X* and
is weakly null in X* and ![]() is weakly Cauchy in
is weakly Cauchy in ![]() [8] . A Banach space
[8] . A Banach space ![]() has property
has property ![]() if each operator
if each operator ![]() is weakly compact for every Banach space
is weakly compact for every Banach space ![]() whenever
whenever ![]() is unconditionally con- verging [9] .
is unconditionally con- verging [9] .
Examples of Banach spaces which satisfy both property ![]() and the Dunford-Pettis property are
and the Dunford-Pettis property are ![]() and
and![]() .
.
Theorem 2.2 has some corollaries which they are proved at this time. The first part is connected to Dunford-Pettis property.
Corollary 2.3. Let ![]() be a Banach space. Then the following is given:
be a Banach space. Then the following is given:
(i) ![]() has the Dunford-Pettis property provided that
has the Dunford-Pettis property provided that ![]() has property
has property![]() .
.
(ii) ![]() has the Dunford-Pettis property if
has the Dunford-Pettis property if ![]() has property
has property![]() .
.
(iii) ![]() has property
has property ![]() whenever
whenever ![]() has property
has property ![]() and the Dunford- Pettis property.
and the Dunford- Pettis property.
Proof. (i) First we assume that the operator ![]() is weakly compact. Then it is easily seen that
is weakly compact. Then it is easily seen that ![]() is an unconditionally converging operator. Now Theorem 2.2 implies that the operator
is an unconditionally converging operator. Now Theorem 2.2 implies that the operator ![]() is completely continuous, as
is completely continuous, as ![]() has property
has property![]() . Thus the proof is complete and
. Thus the proof is complete and ![]() has the Dunford-Pettis property.
has the Dunford-Pettis property.
(ii) Note that (i) concludes that ![]() has the Dunford-Pettis property, as it has property
has the Dunford-Pettis property, as it has property![]() . Hence
. Hence ![]() has the Dunford-Pettis property [8] and we get the result.
has the Dunford-Pettis property [8] and we get the result.
(iii) Let the operator ![]() be unconditionally converging. Now as
be unconditionally converging. Now as ![]() has property
has property ![]() and the Dunford-Pettis property, then
and the Dunford-Pettis property, then ![]() is weakly compact which implies that it is also completely continuous. Finally Theorem 2.2 gives the result, that is,
is weakly compact which implies that it is also completely continuous. Finally Theorem 2.2 gives the result, that is, ![]() has property
has property![]() .
. ![]()
Note that ![]() has both the Dunford-Pettis property and property
has both the Dunford-Pettis property and property ![]() which implies that it also has property
which implies that it also has property![]() . The converse of Corollary 2.3 (iii) does not hold. In general, it is not true that if
. The converse of Corollary 2.3 (iii) does not hold. In general, it is not true that if ![]() has property
has property![]() , then it also has property
, then it also has property![]() . For example,
. For example, ![]() does not have property
does not have property ![]() although it has property
although it has property ![]() (otherwise its dual
(otherwise its dual ![]() would be weakly sequentially complete [9] which contradicts that
would be weakly sequentially complete [9] which contradicts that ![]() contains a copy of
contains a copy of![]() ).
).
A Banach space ![]() is said to have the Reciprocal Dunford-Pettis property if for every Banach space
is said to have the Reciprocal Dunford-Pettis property if for every Banach space![]() , every completely continuous operator
, every completely continuous operator ![]() is weakly compact. In [2] , Bator, Lewis, and Ochoa, showed that property
is weakly compact. In [2] , Bator, Lewis, and Ochoa, showed that property ![]() implies the Reciprocal Dunford-Pettis property, but generally, the converse of this fact is not true. To see, this inference could be reversed, we begin with a space
implies the Reciprocal Dunford-Pettis property, but generally, the converse of this fact is not true. To see, this inference could be reversed, we begin with a space ![]() containing property
containing property![]() .
.
Corollary 2.4. If ![]() has property
has property ![]() and the Reciprocal Dunford-Pettis property, then
and the Reciprocal Dunford-Pettis property, then ![]() has property
has property![]() .
. ![]()
Proof. Suppose ![]() is an unconditionally converging operator. Since
is an unconditionally converging operator. Since ![]() has property
has property![]() , then by Theorem 2.2,
, then by Theorem 2.2, ![]() is completely continuous. As
is completely continuous. As ![]() has the Reciprocal Dunford-Pettis property, then
has the Reciprocal Dunford-Pettis property, then ![]() is weakly compact. Hence
is weakly compact. Hence ![]() has property
has property![]() .
.
Soyabs, in [10] , introduced a property called the ![]() property. A Banach space
property. A Banach space ![]() has the
has the ![]() property if every linear operator
property if every linear operator ![]() is weakly compact for every Banach space
is weakly compact for every Banach space ![]() whose dual does not contain an isomorphic copy of
whose dual does not contain an isomorphic copy of![]() . If Banach space
. If Banach space ![]() has
has ![]() property, then it has the
property, then it has the ![]() property. Also, E. Saab and P. Saab [11] have introduced the property
property. Also, E. Saab and P. Saab [11] have introduced the property![]() . A Banach space
. A Banach space ![]() has the
has the ![]() property if every operator
property if every operator ![]() is weakly compact. If Banach space
is weakly compact. If Banach space ![]() has
has ![]() property, then it has the
property, then it has the ![]() property [10] , therefore, we immediatly have the following result.
property [10] , therefore, we immediatly have the following result.
Corollary 2.5. Let ![]() be a Banach space with the Reciprocal Dunford-Pettis property and the property (MB). Then we have the following:
be a Banach space with the Reciprocal Dunford-Pettis property and the property (MB). Then we have the following:
(i) Every operator ![]() is weakly compact for every Banach space
is weakly compact for every Banach space ![]() whose dual does not contain an isomorphic copy of
whose dual does not contain an isomorphic copy of![]() .
.
(ii) Every operator ![]() is weakly compact.
is weakly compact.
Remebering that, Banach spaces which does not contain a copy of![]() , have the Reciprocal Dunford-Pettis property. Certainly, Odell’s result ( [12] , p. 377) implies that, for any Banach space
, have the Reciprocal Dunford-Pettis property. Certainly, Odell’s result ( [12] , p. 377) implies that, for any Banach space![]() , each operator
, each operator ![]() from
from ![]() to
to ![]() is compact provided it is completely continuous if and only if
is compact provided it is completely continuous if and only if ![]() does not embed in
does not embed in![]() . Also, Rosenthal and Dor's Theorem [3] , if
. Also, Rosenthal and Dor's Theorem [3] , if ![]() is a Banach space and
is a Banach space and ![]() is a sequence in
is a sequence in ![]() such that fails to have a weak Cauchy subsequence, then
such that fails to have a weak Cauchy subsequence, then ![]() has a subsequence which is equivalent to the unit vector of
has a subsequence which is equivalent to the unit vector of![]() , is required for the following consequence. Note that Banach space
, is required for the following consequence. Note that Banach space ![]() has the property
has the property ![]() but does not contain
but does not contain![]() , see [13] (Corollary 2.3 (i)).
, see [13] (Corollary 2.3 (i)).
Theorem 2.6. Suppose that ![]() has property
has property![]() . Then we have the following:
. Then we have the following:
(i) If ![]() does not contain
does not contain![]() , then every unconditionally converging operator
, then every unconditionally converging operator ![]() is compact for every Banach space
is compact for every Banach space![]() .
.
(ii) If ![]() does not contain
does not contain![]() , then every operator
, then every operator ![]() is completely continuous.
is completely continuous.
Proof. (i) Suppose ![]() is an unconditionally converging operator. By Theo- rem 2.2,
is an unconditionally converging operator. By Theo- rem 2.2, ![]() is completely continuous, since
is completely continuous, since ![]() has property
has property![]() . As
. As ![]() does not contain
does not contain![]() ,
, ![]() is a compact operator ( [12] , p. 377).
is a compact operator ( [12] , p. 377).
(ii) Suppose by contradiction that ![]() is not completely continuous operator. Let
is not completely continuous operator. Let ![]() be a weakly null sequence in
be a weakly null sequence in ![]() and
and ![]() for some
for some![]() . Choose
. Choose ![]() so that
so that![]() . Since
. Since![]() , by Rosenthal-Dor Theo- rem, we may assume that
, by Rosenthal-Dor Theo- rem, we may assume that ![]() is weakly Cauchy. By corollary 2.3,
is weakly Cauchy. By corollary 2.3, ![]() has the Dunford-Pettis property, hence
has the Dunford-Pettis property, hence![]() , that is a contradiction.
, that is a contradiction. ![]()
Theorem 2.6 has an immediate consequence; thus the proof is omitted.
Corollary 2.7. Suppose that ![]() has property
has property![]() , then every operator
, then every operator ![]() is completely continuous for every separable dual space
is completely continuous for every separable dual space![]() .
.
Cite this paper
Bahreini, M.E. (2016) Space of Operators and Property
. Advances in Pure Mathematics, 6, 948-953. http://dx.doi.org/10.4236/apm.2016.613072
References
- 1. Saab, P. and Smith, B. (1992) Spaces on Which Every Unconditionally Converging Operators Are Weakly Completely Continuous. Rocky Mountain Journal of Mathematics, 22, 1001-1009.
https://doi.org/10.1216/rmjm/1181072710
- 2. Bator, E., Lewis, P. and Ochoa, J. (1998) Evaluation Maps, Restriction Maps, and Compactness. Colloquium Mathematicum, 78, 1-17.
- 3. Diestel, J. (1984) Sequences and Series in Banach Spaces. Grad Texts in Math, No. 92, Springer-Verlag, Berlin.
https://doi.org/10.1007/978-1-4612-5200-9
- 4. Dunford, N. and Schwartz, J.T. (1958) Linear Operators, Part I: General Theory. Wiley-Interscience, New York.
- 5. Bator, E.M. (1987) Remarks on Completely Continuous Operators. Bulletin of the Polish Academy of Sciences Mathematics, 37, 409-413.
- 6. Emmanuele, G. (1986) A Dual Characterization of Banach Spaces not Containing . Bulletin of the Polish Academy of Sciences Mathematics, 34, 155-160.
- 7. Emmanuele, G. (1991) On the Reciprocal Dunford-Pettis Property in Projective Tensor Products. Mathematical Proceedings of the Cambridge Philosophical Society, 109, 161-166.
https://doi.org/10.1017/S0305004100069632
- 8. Diestel, J. (1980) A Survey of Results Related to the Dunford-Pettis Property. Contemporary Math., 2, 15-60.
https://doi.org/10.1090/conm/002/621850
- 9. Pelczyinski, A. (1962) Banach Spaces on Which Every Unconditionally Converging Operator Is Weakly Compact. Bull. Acad. Polon. Sci. Ser. Sci. Math. Astronom. Phys., 10, 641-648.
- 10. Soyabs, D. (2012) The (D) Property in Banach Spaces. Abstract and Applied Analysis.
- 11. Saab, E. and Saab, P. (1993) Extensions of Some Classes of Operators and Applications. Rocky Mountain Journal of Mathematics, 23, 319-337.
- 12. Rosenthal, H. (1977) Pointwise Compact Subsets of the First Baire Class. American Journal of Mathematics, 99, 362-377.
https://doi.org/10.2307/2373824
- 13. Pelczyinski, A. and Semadeni, Z. (1959) Spaces of Continuous Functions (III). Studia Mathematica, 18, 211-222.




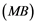 , will be introduced. It is stated that a space
, will be introduced. It is stated that a space  has property
has property  if every
if every 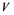 -subset of
-subset of 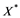 is an
is an 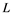 -subset of
-subset of . We describe those spaces which have property
. We describe those spaces which have property . Also, we show that if a Banach space
. Also, we show that if a Banach space 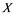 has property
has property 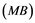 and Banach space
and Banach space  does not contain
does not contain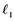 , then every operator
, then every operator 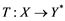 is completely continuous.
is completely continuous. -Sets,
-Sets,  -Sets, Completely Continuous Operators, Unconditionally Converging Operators
-Sets, Completely Continuous Operators, Unconditionally Converging Operators
 -sets,
-sets, 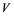 -sets will be studied.
-sets will be studied.