ABSTRACT

In this paper we show that, under some conditions, if M is a manifold with Bakry- Émery Ricci curvature bounded below and with bounded potential function then M is compact. We also establish a volume comparison theorem for manifolds with nonnegative Bakry-Émery Ricci curvature which allows us to prove a topolological rigidity theorem for such manifolds.

Keywords:

Bakry Émery Ricci Curvature, Myers Theorem, Volume Comparison Theorem, Topological Rigidity Theorem

1. Introduction

Let be a complete Riemannian manifold and a smooth function. A Bakry-Émery Ricci curvature is defined by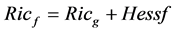, where 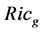stands the Ricci curvature of 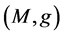and 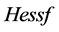denotes the Hessian of f. The function f is called the potential function. For simplicity, denote 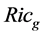by.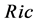

The Bakry-Émery tensor occurs in many different subjects, such as diffusion processes and Ricci flow.

When f is a constant function, the Bakry-Émery Ricci tensor becomes the Ricci tensor so it is natural to investigate which geometric and topological results for the Ricci tensor extend to the Bakry-Émery Ricci tensor.

As an extension of Ricci curvature, many classical results in Riemannian geometry asserted in terms of Ricci curvature have been extended to the analogous ones on Bakry-Émery Ricci curvature condition.

In [1] G. Wei and W. Wylie proved some comparison theorems for smooth metric measure spaces with Bakry-Émery Ricci tensor bounded below. In this paper we establish a Myers type theorem for manifolds bounded below by a negative constant. Therefore we prove that is a generalization of the theorem of M. Limoncu in [2] or H. Tadano in [3] .

In the second part of this paper we establish a condition on noncompact manifold with nonnegative Bakry-Émery Ricci curvature to be diffeomorphic to the euclidean space.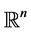

2. Mains Results

The following theorem is a similar theorem proved in [4] and [5] and is a generalization of Myers theorem.

Theorem 2.1. Let 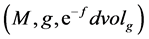be a metric space such that. Suppose that M contains a ball 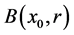of center and radius r such that the mean curvature 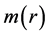of the geodesic sphere 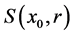with respect the inward pointing normal vector verifies.

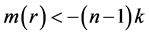If there exists a constant c ≥ 0 such that then M is compact and

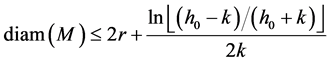(1)

where

It is well known that there exist noncompact manifolds with nonnegative Ricci curvature which are not finite topological type. Recall that a manifold M is said to have finite topological type if there is a compact domain whose boundary is a topological manifold such that is homeomorphic to. An important result about topological finiteness of a complete Riemannian manifold M is due to Abresch and Gromoll (See [6] ).

Let f be a potential function on M satisfying for some nonnegative constant c and a fixed point p.

Set; let and.

In this paper we show a topological rigidity theorem for noncompact manifolds with nonnegative Bakry-Émery Ricci curvature as follow:

Theorem 2.2. Let be a metric space such that. Suppose and for a point and. If for all

(2)

then M is diffeomorphic to.

3. Proofs

Proof of theorem 2.1. The techniques used in the proof of this theorem are based on [4] and [5] . First, let construct a comparison model space. Let be the unit sphere in and take a real r and so that. Let be the solution of the differential equation

(3)

with initial values and. Suppose for all. Hence

(4)

On we define a Riemannian metric tensor by

(5)

where is the standard metric on.

Thus the Riemannian incomplete manifold is with Ricci curvature constant equal to.

For all, the hypersurface of with mean curvature vector with outward pointing vector i.e. with pointing positive s

(6)

Now let prove, under the hypotheses of theorem2.1, that M is compact.

Let y be an arbitrary point in; there exists a point such that. Let be a minimal geodesic joining x to y; with and.

Let be a parallel orthonormal frame along and set

. Hence is a -Jacobi field along. The geodesic

can be extend to a minimal geodesic starting at p: with (see [4] , Proposition 3) and is a -Jacobi field along if and only if can be extended to a Jacobi field along, null at p.

In the geodesic polar coordinates the volume element can be written as:

(7)

where is the volume form on the unit sphere and . Hence . We have

(8)

(9)

To prove the theorem 2.1 we use the following theorem proved by G. Wei and W. Wylie in [1] .

Theorem 3.1. (Mean Curvature Comparison). Let p be a point in M. Assume

(10)

1) If along a minimal geodesic segment from p (when assume) then

(11)

along that minimal geodesic segment from p. Equality holds if and only if the radial sectional curvatures are equal to H and for all.

2) If along a minimal geodesic segment from p and or and then

(12)

along that minimal geodesic segment from p.

3) If along a minimal geodesic segment from p and and then

(13)

In particular when we have

(14)

where is the mean curvature of the geodesic sphere in the simply connected model space of dimension with constant curvature H and is the mean curvature of the model space of dimension n.

In fact in [1] G. Wei and W. Wylie stated that, if then

(15)

where is the solution of equation

From theorem 3.1 above and Equations ((8) and (9)) for all, we have:

(16)

where denotes the volume element in the space of dimension and constant Ricci curvature. From the assumption we have: .

If then when

Hence there exists so that which means that there exists so that the -Jacobi field vanishes at. Therefore we conclude that is a conjugate point of the center p of the sphere. Hence ceases to

be minimal, that is and

In [2] M. Limoncu generalized a classical Myers theorem by using the Bakry-Émery Ricci curvature tensor on complete and connected Riemannian manifolds. This theorem can be viewed as a corollary of theorem 2.1.

Corollary 3.2. Let (M, g) be a complete and connected Riemannian manifold of dimension n. If there exists a smooth function satisfying the inequalities

(17)

and then M is compact.

Proof of Corollary

To prove this corollary it suffices to show that there exist a positive real with and a geodesic sphere which mean curvature verifies .

Let x be a point in M and let be a minimal geodesic joining p to x and be a parallel orthonormal vector fields along orthonormal to.

Set where. We have

(18)

Therefore

(19)

which allows that if.

By Compactness of, there exists a positive constant so that, for any geodesic emanating from p we have

Since, the conclusion follows from theorem 2.1.

Corollary 3.3. (E. Calabi)

Let be a complete and connected Riemannian manifold of dimension n. Suppose there exists a smooth function so that and. If M is noncompact then there exists a geodesic in M so that .

Proof

It is clear that, if for a geodesic issuing from p there exist two positive reals k and r so that for all then p admits a conjugate point along. Hence, if M is noncompact, for all, there exists a geodesic issuing from p so that for any two positive real k and r there exists so that.

In particular if we take and the conclusion follows.

Corollary 3.4. (Ambrose)

Let be a complete and connected Riemannian manifold of dimension n. Suppose there exists a function f on M so that. If there exists a point p in M so that, for any geodesic emanating from p, parametrized by it’s arc-length we have

(20)

then M is compact.

Proof

If M is noncompact, from corollary 3.3, there exists so that for. Therefore,

(21)

Proof of theorem 2.2

Let denotes the weighted volume of the geodesic ball of center p and radius s in M and the volume of geodesic ball of radius s in the model space with constant curvature H and dimension m.

In Differential Geometry, the volume comparison theory plays an important rule. Many important results in this topic can not be obtained without volume comparison results as topological rigidity results.

For complete smooth metric measure space with the following lemma improved the volume comparison theorem proved by G. Wei and W. Wylie In [1] :

Lemma 3.5. Let be complete smooth metric measure space with. Fix; if there exists c so that then for

(22)

Proof

Let x be a point in M and let be a minimal geodesic joining p to x and be a parallel orthonormal vector fields along orthonormal to.

Set.

By the second variation formula we have:

(23)

Hence. From (9) and the above relation, we have

For all positive reals r and s, integrating this relation we have:

(24)

Therefore we have Hence

(25)

which implies

(26)

and integrating from 0 to with respect to s we obtain the conclusion.

Set. Then

(27)

Hence we have

(28)

From the relation (28) we deduce that the function is nonincreasing.

Let and

We have.

We say that M is of large weighted volume growth if.

Let be the set of the unit initial tangent vectors to the geodesics starting from p which are minimized at least to t and its complementary set. Set

(29)

Let a subset of the unit sphere. Set

(30)

Lemma 3.6. If and then

1) the function is nonincreasing and

2) for any, where h is defined by: .

Proof

By Equation (27) we have

(31)

hence we deduce that the function is decreasing.

By lemma 3 in [7] we have:

(32)

Therefore

(33)

For we have and by part (1) of the lemma 3.6 we have:

(34)

and the part (2) can be proved as the lemma 3.10 in [8] .

Lemma 3.7. Let be a complete noncompacte Riemannian manifold and f a potential function on M with and. If M is of large weighted volume then

(35)

Proof

We have

(36)

and

(37)

(38)

Since we have hence

(39)

Lemma 3.8. Let be a complete noncompacte Riemannian manifold and f a potential function on M with and. If M is of large weighted volume then for any we have

(40)

The proof of this lemma is step by step similar to the one in [9] (lemma 2.4).

Let be two points in M. The excess function is defined as:

(41)

By triangle inequality the excess function is nonnegative and is lipschitz. Let be a ray from p and set. Hence, for any we have:

(42)

The function is nonincreasing on t and

Set

By the fact that is nonincreasing on t, we have

Applying the Toponogov’s theorem and the definition of critical point we have:

Lemma 3.9. Let M be a complete noncompacte Riemannian manifold such that for some and. Suppose that is a critical point of. Then for any ray issuing from p, we have

(43)

Recall that a point x is a critical point of if for any vector there exists

a minimal geodesic from x to p so that

From the inequality (28) and using the arguments of the proof of the Proposition 2.3 in [6] , we deduce the following excess estimate for complete smooth metric measure space with and potential function bounded by.

Theorem 3.10. Let be a complete noncompacte Riemannian manifold and f a potential function on M with for some fixed point p, and then

(44)

By the same arguments as in [10] and using instead of, one can prove the above lemma.

To prove the theorem 2.2, it suffices to show that M contains no critical point of other than p.

For this, let x be a point in M and and set. From the lemma 3.8 and the inequality (2) we have:

(45)

hence, there exists a ray issuing from p verifying

(46)

Let q be a point on so that then. From the triangle inequality we have: for all, which means. Such from the relations (44) and (45) we obtain

(47)

The inequalities (43) and (47) show that x is not a critical point of. Hence, by isotopy lemma M is diffeomorphic to.

Cite this paper

Kaboye, I.A. and Mahaman, B. (2016) Manifolds with Bakry-Emery Ricci Curvature Bounded Below. Advances in Pure Mathematics, 6, 754-764. http://dx.doi.org/10.4236/apm.2016.611061

References