Received 7 July 2016; accepted 12 August 2016; published 15 August 2016

ABSTRACT

In this paper, we shall present the strong laws of large numbers for fuzzy set-valued random variables in the sense of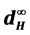. The results are based on the result of single-valued random variables obtained by Taylor [1] and set-valued random variables obtained by Li Guan [2] .

Keywords:

Laws of Large Numbers, Fuzzy Set-Valued Random Variable, Hausdorff Metric

1. Introduction

With the development of set-valued stochastic theory, it has become a new branch of probability theory. And limits theory is one of the most important theories in probability and statistics. Many scholars have done a lot of research in this aspect. For example, Artstein and Vitale in [3] had proved the strong law of large numbers for independent and identically distributed random variables by embedding theory. Hiai in [4] had extended it to separable Banach space. Taylor and Inoue had proved the strong law of large numbers for independent random variable in the Banach space in [5] . Many other scholars also had done lots of works in the laws of large numbers for set-valued random variables. In [2] , Li proved the strong laws of large numbers for set-valued random variables in 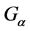space in the sense of d_H metric.

As we know, the fuzzy set is an extension of the set. And the concept of fuzzy set-valued random variables is a natural generalization of that of set-valued random variables, so it is necessary to discuss convergence theorems of fuzzy set-valued random sequence. The limits of theories for fuzzy set-valued random sequences are also been discussed by many researchers. Colubi et al. [6] , Feng [7] and Molchanov [8] proved the strong laws of large numbers for fuzzy set-valued random variables; Puri and Ralescu [9] , Li and Ogura [10] proved convergence theorems for fuzzy set-valued martingales. Li and Ogura [11] proved the SLLN of [12] in the sense of by using the “sandwich” method. Guan and Li [13] proved the SLLN for weighted sums of fuzzy set- valued random variables in the sense of 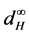which used the same method. In this paper, what we concerned are the convergence theorems of fuzzy set-valued sequence in 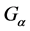space in the sense of.

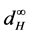The purpose of this paper is to prove the strong laws of large numbers for fuzzy set-valued random variables in 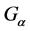space, which is both the extension of the result in [1] for single-valued random sequence and also the extension in [2] for set-valued random sequence.

This paper is organized as follows. In Section 2, we shall briefly introduce some concepts and basic results of set-valued and fuzzy set-valued random variables. In Section 3, I shall prove the strong laws of large numbers for fuzzy set-valued random variables in 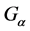space, which is in the sense of Hausdorff metric.

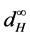2. Preliminaries on Set-Valued Random Variables

Throughout this paper, we assume that 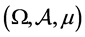is a complete probability space, 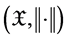is a real separable

Banach space, 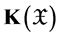is the family of all nonempty closed subsets of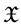, and 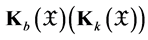is the family

of all non-empty bounded closed(compact) subsets of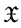, and is the family of all non-empty compact convex subsets of.

Let A and B be two nonempty subsets of and let, the set of all real numbers. We define addition and scalar multiplication by

The Hausdorff metric on is defined by

for. For an A in, let.

The metric space is complete, and is a closed subset of (cf. [14] ,

Theorems 1.1.2 and 1.1.3). For more general hyperspaces, more topological properties of hyperspaces, readers may refer to the books [15] and [14] .

For each, define the support function by

where is the dual space of.

Let denote the unit sphere of, the all continuous functions of, and the norm is defined

as

The following is the equivalent definition of Hausdorff metric.

For each,

A set-valued mapping is called a set-valued random variable (or a random set, or a multi-

function) if, for each open subset O of,.

For each set-valued random variable F, the expectation of F, denoted by, is defined by

where is the usual Bochner integral in, the family of integrable -valued random variables,

and.

Let denote the family of all functions which satisfy the following conditions:

1) The level set.

2) Each v is upper semicontinuous, i.e. for each, the level set is a closed subset of.

3) The support set is compact.

A function v in is called convex if it satisfies

for any.

Let be the subset of all convex fuzzy sets in.

It is known that v is convex in the above sense if and only if, for any, the level set is a convex subset of (cf. Theorem 3.2.1 of [16] ). For any, the closed convex hull of v is

defined by the relation for all.

For any two fuzzy sets define

for any

Similarly for a fuzzy set and a real number, define

for any

The following two metrics in which are extensions of the Hausdorff metric d_H are often used (cf. [17] and [18] , or [14] ): for,

Denote, where is the fuzzy set taking value one at 0 and zero for all

. The space is a complete metric space (cf. [18] , or [14] : Theorem 5.1.6) but not separable (cf. [17] , or [14] : Remark 5.1.7).

It is well known that, for every. Due to the completeness of, every

Cauchy sequence has a limit v in.

A fuzzy set-valued random variable (or a fuzzy random set, or a fuzzy random variable in literature) is a mapping, such that is a set-valued random variable for every (cf. [18] or [14] ).

The expectation of any fuzzy set-valued random variable X, denoted by, is an element in such that, for every,

where the expectation of right hand is Aumann integral. From the existence theorem (cf. [19] ), we can get an equivalent definition: for any,

Note that is always convex when is nonatomic.

3. Main Results

In this section, we will give the limit theorems for fuzzy set-valued random variables in space. I will firstly introduce the definition of space. The following Definition 3.1 and Lemma 3.2 are from Taylor’s book [8] , which will be used later.

Definition 3.1. A Banach space is said to satisfy the condition for some. If there exists a mapping, such that

1);

2);

3), for all and some positive constant A.

Note that Hilbert spaces are with constant and identity mapping G.

Lemma 3.2. Let be a Banach space which satisfies the condition of, be independent

random elements in, such that and for each. Then

where A is the positive constant in 3) of definition 3.1.

In order to obtain the main results, we firstly need to prove Lemma 3.5. The following lemma are from [14] (cf. p89, Lemma 3.1.4), which will be used to prove Lemma 3.5.

Lemma 3.3. Let be a sequence in. If

for some, then

Lemma 3.4. (cf. [13] ) For any, there exists a finite, such that

Now we prove that the result of Lemma 3.3 is also true for fuzzy sets.

Lemma 3.5. Let be a sequence in. If

(3.1)

for some, then

Proof. By (3.1), we can have

and

for. Then by Lemma 3.3, for, we have

and

By Lemma 3.4, take an, there exists a finite, such that

Then for,

Consequently,

Since the first two terms on the right hand converge to 0 in probability one, we have

but is arbitrary and the result follows. ,

Theorem 3.6. Let be a Banach space which satisfies the condition of, let be independent fuzzy set-valued random variables in, such that for any n. If

where for 0 ≤ t ≤ 1 and for t ≥ 1, then converges with probability 1 in the sense of.

Proof. Define

Note that for each j, and both and are independent sequence of

fuzzy set-valued random variables. When, we have, and. Then, for any

And from, we know that is a Cauchy sequence. So, we have

Since convergence in the mean implied convergence in probability, Ito and Nisios result in [9] for independent random elements (cf. Section 4.5) provides that

So, for any n, m ≥ 1, m > n, by triangle inequality we have

It means is a Cauchy sequence in the sense of. By the completeness of, we have converges almost everywhere in the sense of.

Next we shall prove that converges in the sense of. Firstly, we assume that are all convex fuzzy set-valued random variables. Then by the equivalent definition of Hausdorff metric, we have

For any fixed n, m, there exists a sequence, such that

That means there exist a sequence, such that

Then by Cr inequality, dominated convergence theorem and Lemma 3.2, we have

for each n and m.

Then, we know is a Cauchy sequence. Hence, is a Cauchy sequence. Thus by the similar way as above to prove converges with probability 1 in the sense of. We also can prove that

with probability 1 in the sense of. In fact, for each,

So, we can prove that

with probability 1 in the sense of. If are not convex, we can prove converges with probability 1 in the sense of as above, and by the Lemma 3.5, we can prove that converges with proba-

bility 1 in the sense of. Then the result was proved. ,

From Theorem 3.6, we can easily obtain the following corollary.

Corollary 3.7. Let be a separable Banach space which is for some. Let be

a sequence of independent fuzzy set-valued random variables in, such that for each n. If

are continuous and such that and are non-decreasing, then for each

the convergence of

implies that

converges with probability one in the sense of.

Proof. Let

If, by the non-decreasing property of, we have

That is

(4.1)

If, by the non-decreasing property of, we have

That is

(4.2)

Then as the similar proof of Theorem 3.6, we can prove both and converges with probability

one in the sense of, and the result was obtained. ,

Acknowledgements

We thank the Editor and the referee for their comments. Research of Li Guan is funded by the NSFC (11301015, 11571024, 11401016).

Cite this paper

Lamei Shen,Li Guan, (2016) Strong Laws of Large Numbers for Fuzzy Set-Valued Random Variables in G_α Space. Advances in Pure Mathematics,06,583-592. doi: 10.4236/apm.2016.69047

References