Advances in Pure Mathematics
Vol.06 No.07(2016), Article ID:67409,9 pages
10.4236/apm.2016.67036
An Efficient Adaptive Iteratively Reweighted l1 Algorithm for Elastic lq Regularization
Yong Zhang, Wanzhou Ye
Department of Mathematics, College of Science, Shanghai University, Shanghai, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 May 2016; accepted 13 June 2016; published 16 June 2016
ABSTRACT
In this paper, we propose an efficient adaptive iteratively reweighted 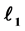 algorithm (A-IRL1 algorithm) for solving the elastic
algorithm (A-IRL1 algorithm) for solving the elastic 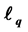 regularization problem. We prove that the sequence generated by the A-IRL1 algorithm is convergent for any rational
regularization problem. We prove that the sequence generated by the A-IRL1 algorithm is convergent for any rational  and the limit is a critical point of the elastic
and the limit is a critical point of the elastic 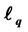 regularization problem. Under certain conditions, we present an error bound for the limit point of convergent sequence.
regularization problem. Under certain conditions, we present an error bound for the limit point of convergent sequence.
Keywords:
Compressed Sensing, Elastic 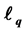 Minimization, Nonconvex Optimization, Convergence, Critical Point
Minimization, Nonconvex Optimization, Convergence, Critical Point

1. Introduction
Compressed sensing (CS) has been emerging as very active research field and brings about great changes in the fields of signal processing in recent years [1] [2] . The main task of CS focuses on the recovery of sparse signal from a small number of linear measurement data. It can be mathematically modeled as following optimization problem,
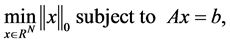 (1)
(1)
where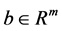 ,
, 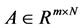 (commonly
(commonly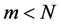 ) is a measurement matrix and
) is a measurement matrix and , formally called the
, formally called the 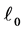 quasi-norm, denotes the number of nonzero components of
quasi-norm, denotes the number of nonzero components of . In general, it is difficult to tackle problem (1) due to its nonsmooth and nonconvex nature. In recent years, some researchers have proposed the
. In general, it is difficult to tackle problem (1) due to its nonsmooth and nonconvex nature. In recent years, some researchers have proposed the 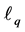 norm regularization problem [3] - [5] with
norm regularization problem [3] - [5] with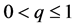 , that is, to consider the following
, that is, to consider the following 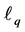 regularization problem
regularization problem

or the unconstrained 

where 


When



In this paper, we consider the following elastic 

where 





Obviously, for



The model (5) can be considered as an approximation to the model (4) as


where the weight 
The adaptive iteratively update of 

The relaxed elastic 


The rest of this paper is organized as follows: In Section 2, we summarize the A-IRL1 algorithm for solving elastic 


2. A-IRL1 Algorithm for Solving Elastic 
We give a detailed implementation of A-IRL1 algorithm (6) for solving elastic 
In Algorithm 1, 




It is clear from Algorithm 1 that 




3. Convergence of Algorithm 1
In this section, we first prove that the the sequence 


Lemma 1. Given 


holds for any
Proof. We first define


The following inequality is always hold for any


Let 


After rewriting the terms of (9), we thus get the desired inequality (7).
Our next result shows the monotonicity of 
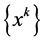
Lemma 2. Let 

Furthermore,

Proof. Since 
Besides, we can get the subgradient of 

Hence, we find

which means that there exists 

where
We compute

Using (14), we have

Substituting (16) into (15) and using Lemma 1 yields

where the first inequality uses 

From Lemma 2 (10), we know that 




In order to prove that the whole sequence generated by Algorithm 1 is convergent, we need the following lemma, which plays an important role in the proof of convergence. The following lemma mainly states that for almost every system of n polynomial equations in n complex variables, if its corresponding highest ordered system of equations have only trivial solution, then there is a finite number of solutions to the n polynomial equations. For detailed proof refer to Theorem 3.1 in [16] .
Lemma 3. ( [16] ) Let n polynomial equations in n complex variables 







With above lemmas, we are now in a position to present the convergence of Algorithm 1 for any rational number 

Theorem 1 For any







Proof. From (10), we know that the sequence 


there exists at least one convergent subsequence. We assume that 














where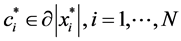
The above Equation (18) demonstrates that the limit of any convergent subsequence of 




A classification is made for the limit point set 

which contains all the limit points with each sparsity s. If we prove the set 


Furthermore, for any given 


From (19) and (20), we have


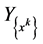
For any 






where 



It is clear that (21) can be rewritten as follows:

where 





where 

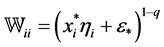






Since all the solutions of Equation (21) satisfy (24), we can thus show that Equation (21) has finite solutions as long as we can prove that (24) has finite solutions. To do that, we show that the following system has finite solutions:

where

To prove that system (26) has only trivial solution, we use the method of proof by contradiction. Without loss of generality, we assume 






where 





matrix B is also positive definite, and thus we have 





Combining with 





Theorem 1 gives a detailed convergence proof of Algorithm 1 based on an algebraic approach. In the next, we will present an error bound between the convergent limit and the sparse solution of problem (1).
Under the Restricted Isometry Property (RIP) on the matrix A, we present an error bound between the convergent limit and the sparse solution of problem (1). First of all, we give a definition of RIP on the matrix A as follows.
Definition: For every integer


for all subsets 
Under the RIP assumption, we can ensure that the limit 

for


With the concept of RIP, we are able to prove the result of following theorem.
Theorem 2. Suppose that x is an s-sparse solution of (1) satisfying



(1) When




(2) When


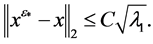
Here



Proof. (1). In Theorem 1, we have proved that the limit 


We use Lemma 2 to get

where we use the assumption that the initial value 


et S be the index set of the s-sparse solution x, and let 


Letting 

(3) If












where the third inequality uses (31) with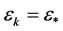



Under the condition of RIP on the matrix A, when

4. Conclusion
The iteratively reweighted 








Cite this paper
Yong Zhang,Wanzhou Ye, (2016) An Efficient Adaptive Iteratively Reweighted l1 Algorithm for Elastic lq Regularization. Advances in Pure Mathematics,06,498-506. doi: 10.4236/apm.2016.67036
References
- 1. Donoho, D.L. (2006) Compressed Sensing. IEEE Transactions on Information Theory, 52, 1289-1306.
http://dx.doi.org/10.1109/TIT.2006.871582 - 2. Candès, E., Romberg, J. and Tao, T. (2006) Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Transactions on Information Theory, 52, 489-509.
http://dx.doi.org/10.1109/TIT.2005.862083 - 3. Chartrand, R. (2007) Exact Reconstruction of Sparse Signals via Nonconvex Minimization. IEEE Signal Processing Letters, 14, 707-710.
http://dx.doi.org/10.1109/LSP.2007.898300 - 4. Xu, Z.B., Chang, X.Y., Xu, F.M. and Zhang, H. (2012) L1/2 Regularization: A Thresholding Representation Theory and a Fast Solver. IEEE Transactions on Neural Networks and Learning Systems, 23, 1013-1027.
http://dx.doi.org/10.1109/TNNLS.2012.2197412 - 5. Foucart, S. and Lai, M. (2009) Sparsest Solutions of Underdetermined Linear Systems via lq Minimization for 0<q≤1. Applied and Computational Harmonic Analysis, 26, 395-407.
http://dx.doi.org/10.1016/j.acha.2008.09.001 - 6. Chen, S.S., Donoho, D.L. and Saunders, M.A. (1998) Atomic Decomposition by Basis Pursuit. SIAM Journal on Scientific Computing, 20, 33-61.
http://dx.doi.org/10.1137/S1064827596304010 - 7. Daubechies, I., Defrise, M. and Christine, D.M. (2004) An Iterative Thresholding Algorithm for Linear Inverse Problems with a Sparsity Constraint. Communications on Pure and Applied Mathematics, 57, 1413-1457.
http://dx.doi.org/10.1002/cpa.20042 - 8. Candes, E.J., Wakin, M.B. and Boyd, S.P. (2008) Enhancing Sparity by Reweighted l1 Minimization. Journal of Fourier Analysis and Applications, 14, 877-905.
http://dx.doi.org/10.1007/s00041-008-9045-x - 9. Daubechies, I., Devore, R., Fornasier, M. and Güntük, C.S. (2010) Iteratively Reweighted Least Suqares Minimization for Sparse Recovery. Communications on Pure and Applied Mathematics, 63, 1-38.
http://dx.doi.org/10.1002/cpa.20303 - 10. Zou, H. and Hastie, T. (2005) Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society: Series B, 67, 301-320.
http://dx.doi.org/10.1111/j.1467-9868.2005.00503.x - 11. Tibshirani, R. (1996) Regression Shrinkage and Selection via The Lasso. Journal of the Royal Statistical Society: Series B, 58, 267-288.
- 12. Jin, B.T., Lorenz, D.A. and Schiffler, S. (2009) Elastic-Net Regularization: Error Estimates and Active Set Methods. Inverse Problems, 25, Article ID: 115022.
http://dx.doi.org/10.1088/0266-5611/25/11/115022 - 13. De Mola, C., De Vitob, E. and Rosasco, L. (2009) Elastic-Net Regularization in Learning Theory. Journal of Complexity, 25, 201-230.
http://dx.doi.org/10.1016/j.jco.2009.01.002 - 14. Lai, M.J., Xu, Y.Y. and Yin, W.T. (2013) Improved Iteratively Reweighted Least Squares for Unconstrained Smoothed lq Minimization. SIAM Journal on Numerical Analysis, 51, 927-957.
http://dx.doi.org/10.1137/110840364 - 15. Donoho, D.L. and Tsaig, Y. (2008) Fast Solution of l1 Norm Minimization Problems When the Solution May Be Sparse. IEEE Transactions on Information Theory, 54, 4789-4812.
http://dx.doi.org/10.1109/TIT.2008.929958 - 16. Garcia, C.B. and Li, T.Y. (1980) On the Number of Solutions to Polynomial Systems of Equations. SIAM Journal on Numerical Analysis, 17, 540-546.
http://dx.doi.org/10.1137/0717046












