Advances in Pure Mathematics
Vol.06 No.06(2016), Article ID:66567,16 pages
10.4236/apm.2016.66029
On Hom-Lie Pseudo-Superalgebras
Shengxiang Wang1,2, Tingting Tao2*
1Department of Mathematics, Nanjing University, Nanjing, China
2School of Mathematics and Finance, Chuzhou University, Chuzhou, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 March 2016; accepted 16 May 2016; published 19 May 2016
ABSTRACT
The aim of this article is to introduce the notion of Hom-Lie H-pseudo-superalgebras for any Hopf algebra H. This class of algebras is a natural generalization of the Hom-Lie pseudo-algebras as well as a special case of the Hom-Lie superalgebras. We present some construction theorems of Hom- Lie H-pseudo-superalgebras, reformulate the equivalent definition of Hom-Lie H-pseudo-super- algebras, and consider the cohomology theory of Hom-Lie H-pseudo-superalgebras with coefficients in arbitrary Hom-modules as a generalization of Kac’s result.
Keywords:
Hom-Associative Pseudo-Superalgebra, Hom-Lie Pseudo-Superalgebra, Hom-Lie Conformal Superalgebra, Hom-Annihilation Superalgebra, Cohomology

1. Introduction
The notion of conformal algebras [1] - [5] was introduced by Kac as a formal language describing the singular part of the operator product expansion in two-dimensional conformal field theory, and it came to be useful for investigation of vertex algebras (see [6] - [8] ). The concept of vertex algebras was derived from mathematical physics; it was first mathematically defined and considered by Borcherds in [9] to obtain his solution of the Moonshine conjecture in the theory of finite simple groups.
As a generalization of conformal algebras, Bakalov, D’Andrea and Kac [10] developed a theory of “multi- dimensional” lie conformal algebras, called Lie H-pseudo-algebras for any Hopf algebra H. Classification problems, cohomology theory and representation theory have been considered in [10] - [12] . In [13] , Boyallian and Liberati studied pseudo-algebras from the point of view of pseudo-dual of classical Lie coalgebra structures by defining the notions of Lie H-coalgebras and Lie pseudo-bialgebras.
In [14] , Sun generalized the pseudo-algebra structures to the Hom-pseudo-algebras of associative and Lie type, and showed some examples of the new structures and construction theorems. Hom-algebras were firstly studied by Hartwig, Larsson and Silvestrov in [15] , where they introduced the structure of Hom-Lie algebras in the context of the deformations of Witt and Virasoro algebras. Later, Larsson and Silvestrov extended the notion of Hom-Lie algebras to quasi-Hom Lie algebras and quasi-Lie algebras (see [16] ). Recently, Yau laid the foundation of a homology theory for Hom-Lie algebras and constructed the enveloping algebras of Hom-Lie and Hom-Leibniz algebras in [17] - [19] . Many more properties and structures of Hom-Lie algebras have been developed (see [20] - [23] and references cited therein).
In [24] , Hom-algebras and Hom-coalgebras were introduced by Makhlouf and Silvestrov as a generalization of ordinary algebras and coalgebras in the following sense: the associativity of the multiplication was replaced by the Hom-associativity and similar for Hom-coassociativity. They also defined the structures of Hom-bialgebras and Hom-Hopf algebras, and described some of their properties extending properties of ordinary bialgebras and Hopf algebras in [25] and [26] . Different to Makhlouf and Silvestrov’s work, Caenepeel and Goyvaerts studied the Hom-Hopf algebras from a categorical view point in [27] , and called them monoidal Hom-bialgebras and monoidal Hom-Hopf algebras respectively (for more details about monoidal Hom-Hopf algebras, see references [28] - [32] and references cited therein).
In [33] , Ammar and Makhlouf introduced the notion of Hom-Lie superalgebras and provided a construction theorem from which one can derive a one parameter family of Hom-Lie superalgebras deforming the orthosymplectic Lie superalgebras. The notion of Hom-Lie superalgebras is a natural and meaningful generalization of Lie superalgebras which were introduced by Kac in [3] . Motivated by [4] [10] , in which Kac formulated the notion of conformal superalgebras and considered the classification theorem and representation theory of conformal superalgebras. We think whether we can extend the notions of Hom-Lie pseudo-algebras and conformal superalgebras to Hom-Lie pseudo-superalgebras.
Cohomology is an important tool in mathematics. Its range of applications contains algebra and topology as well as the theory of smooth manifolds or of holomorphic functions. The cohomology theory of Lie algebras was developed by Chevalley, Eilenberg and Cartan. Scheunert and Zhang introduced and investigated the cohomology groups of Lie superalgebras in [34] . Naturally, we think whether we can extend the notion of cohomology groups to Hom-Lie H-pseudo-superalgebras. This becomes our second motivation of the paper.
To give a positive answer to the questions above, we organize this paper as follows. In Section 2, we recall some basic definitions about Lie pseudo-algebras. In Section 3, we define Hom-Lie pseudo-superalgebras and introduce two construction theorems of Hom-Lie pseudo-superalgebras (see Proposition 3.12 and Theorem 3.13). In Section 4, we mainly discuss the annihilation superalgebras of Hom-pseudo-superalgebras (see Proposition 4.5). In Section 5, we determine some equivalent definitions of Hom-pseudo-superalgebras. In Section 6, we discuss the cohomology of Hom-Lie H-pseudo-superalgebras (see Theorem 6.1).
2. Preliminaries
In this section we recall some basic definitions and results related to our paper. Throughout the paper, all algebraic systems are supposed to be over a field k of characteristic 0, H always denotes a Hopf algebra with an antipode S. We summarize in the following the ungraded definitions of Hom-associative and Hom-Lie H-pseudo- algebras (see [14] ). The reader is referred to Sweedler [35] about Hopf algebras, the Sweedler-type notation for the comultiplication is denoted by: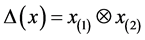 .
.
Recall that a pseudotensor category 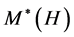 is a category whose objects are the same objects as in the category
is a category whose objects are the same objects as in the category 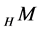 of left H-modules, but with a non-trivial pseudotensor structure, see [10] .
of left H-modules, but with a non-trivial pseudotensor structure, see [10] .
A Hom-associative H-pseudo-algebra [14] is a triple 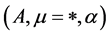 consisting of a linear space A in
consisting of a linear space A in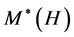 , an operation
, an operation 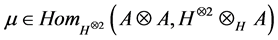 and a homomorphism
and a homomorphism 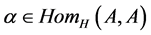 satisfying
satisfying
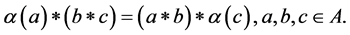 (2.1)
(2.1)
A Hom-Lie H-pseudo-algebra [14] is a triple 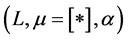 consisting of a linear space L in
consisting of a linear space L in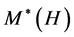 , an operation
, an operation 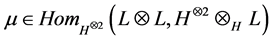 and a homomorphism
and a homomorphism 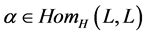 satisfying the following axioms (
satisfying the following axioms (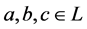 ):
):
1) Skew-commutativity:
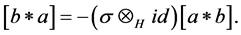 (2.2)
(2.2)
2) Hom-Jacobi identity:
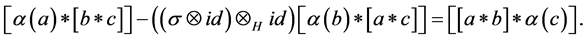 (2.3)
(2.3)
An elementary but important property of Hom-Lie H-pseudo-algebra is that each Hom-associative H-pseudo- algebra gives rise to a Hom-Lie H-pseudo-algebra via the commutator bracket.
A Hom-Lie H-conformal algebra ( [14] ) is a triple 





1) H-sesqui-linearity:

2) Skew-commutativity:

3) Hom-Jacobi identity:

Recall from Sun [14] we know that one can reformulate the definition of a Hom-Lie H-pseudo-algebra via a Hom-Lie H-conformal algebra.
3. Hom-Pseudo Superalgebras of Associative and Lie Types
In this section we will introduce the concept and construction theorems of Hom-H-pseudo-superalgebras of associative and Lie types, and show some examples of Hom-Lie H-pseudo-superalgebras that are neither Hom-Lie superalgebras nor Hom-Lie pseudo-algebras.
Definition 3.1. A Hom-associative H-pseudo-superalgebra is a triple 




in 
Example 3.2. For a one dimensional Hopf algebra H = k, a Hom-associative H-pseudo-superalgebra is just a Hom-associative superalgebra over k. If
A Hom-associative H-pseudo-superalgebra 



Let 



Definition 3.3. Let 









where
Example 3.4. Let 


for all 
Definition 3.5. A Hom-Lie H-pseudo-superalgebra is a triple 



1) Skew-commutativity:

2) Hom-Jacobi identity:

where a, b, c are homogeneous elements in L.
Here and further, 
Example 3.6. For a one dimensional Hopf algebra H = k, a Hom-Lie H-pseudo-superalgebra is just a Hom-Lie superalgebra over k. If
Example 3.7. Let H be a Hopf algebra and 







Example 3.8. Let 


for all 
Example 3.9. Let H be a Hopf algebra and 


In particular, if

A Hom-Lie H-pseudo-superalgebra 



Let 



Definition 3.10. Let 







where
In the following, we will show that the supercommutator bracket defined using the multiplication in a Hom- associative H-pseudo-superalgebra leads naturally to a Hom-Lie H-pseudo-superalgebra.
Lemma 3.11. Let 
1)
2)
3)
Proof. We only prove (3), and similarly for (1), (2). For any homogeneous elements 
On one hand we have
since H is cocommutative. Similarly, we have
as required. So (3) holds since A is Hom-associative. ,
Proposition 3.12. Given any Hom-associative H-pseudo-superalgebra

and then extending by linearity to all elements. Then 
Proof. We shall show that the condition (3.9) leads A to be a Hom-Lie H-pseudo-superalgebra, in the sense of Definition 3.5. For this purpose, we first claim that the bracket pseudoproduct is both H-bilinear and skew- commutative, but these are easy to check. It remains to verify that the conditions (2) of Definition 3.5 are satisfied by the condition (3.9). Now we have the following calculations:
Immediately, we can obtain
It follows from Lemma 3.12 that
Furthermore, we have
Together with the above results, we finally obtain
The proof is completed. ,
Next we will construct Hom-Lie H-pseudo-superalgebras from Lie H-pseudo-superalgebras and even Hom- Lie superalgebra endomorphisms, generalizing the results for Hom-Lie H-pseudo-algebras in [14] and Hom-Lie superalgebras in [33] .
Theorem 3.13. Let 




Moreover, suppose that 





is a morphism of Hom-Lie H-pseudo-superalgebras.
Proof. We shall show that 

Since 
Therefore we have
as needed. To show that f is a morphism of Hom-Lie H-pseudo-superalgebras, we do the calculations:
The proof is completed. ,
To provides another way to construct Hom-Lie H-pseudo-superalgebras and Hom-associative H-pseudo- superalgebras, we first recall the definition of current H-pseudo-algebras in [10] .
Let 




if

Proposition 3.14. Let H' be a Hopf subalgebra of H and 


Proof. We only prove the case of Hom-Lie H'-pseudo-superalgebras, the Hom-associative case is similar. We denote

It is obviously that the skew-commutativity holds since 

Since 
that is,
By the multiplication of
Hence 
4. Hom-Annihilation Superalgebras
In this section we will study the annihilation superalgebras of Hom-H-pseudo-superalgebras. First of all we will give the definition of H-differential superalgebras.
Definition 4.1. An associative superalgebra Y is called an associative H-differential superalgebra if it is a left H-module such that


Let Y be an H-bimodule which is a commutative associative H-differential superalgebra. For a left H-module L, it is easy to see that 



The definition of Hom-Lie H-differential-superalgebras can be obtained similarly.
Proposition 4.2. Let Y be a Hom-Lie H-differential-superalgebra and 


for all 


Proof. First we shall show that AYL is an H-module, but this is easy to check. It remains to verify that the conditions (1) and (2) in Definition 3.5 are satisfied. For this purpose, we take
Since L is a Hom-Lie H-pseudo-superalgebra, then 
as required. Next we verify the Hom-Jacobi identity by the following calculations:
Similarly, by exchanging the status of the element
By the Hom-Jacobi identity of L, we have
Hence
So AYL is a Hom-Lie H-differential superalgebra. This completes the proof. ,
Remark 4.3. In particular, when



Remark 4.4. A similar statement holds for Hom-associative H-pseudo-superalgebras and Hom-modules as well. For example, if 


if 

Proposition 4.5. Let 


if 
Proof. According to the bracket pseudoproduct defined above, it is easy to see that H-bilinearity holds. To verify the Skew-commutativity and Hom-Jacobi identity, take 
Since L is a Hom-Lie H-pseudo-superalgebra, 
That is, the skew-commutativity holds. So it is sufficient to verify the Hom-Jacobi identity. Since
we have
Similarly, by exchanging the status of the element
By the Hom-Jacobi identity of L, we have
it follows that
So AYL is a Hom-Lie H-pseudo-superalgebra. This completes the proof. ,
5. Hom-Lie Conformal Superalgebras
In this section we will reformulate the definition of Hom-Lie (or Hom-associative) H-pseudo-superalgebras. The resulting notion, equivalent to that of Hom-H-pseudo-superalgebras, will be called Hom-H-conformal superalgebras.
Let us start by racalling the definitions of the Fourier transform and the x-brackets in [10] . For an arbitrary Hopf algebra H, the Fourier transform 



In order to reformulate the definition of a Lie (or associative) H-pseudo-algebra, Bakalov, D'Andrea and Kac introduced the bracket 

That is,
Then for
Let 

Then we have
Similarly, we can obtain 
Therefore
is equivalent to
So the definition of Hom-Lie H-pseudo-superalgebra can be equivalently reformulated as follows.
Definition 5.1. A Hom-Lie H-conformal superalgebra is a triple 



1) H-sesqui-linearity:

2) Skew-commutativity:

3) Hom-Jacobi identity:

where a, b, c are homogeneous elements in L and
One can also reformulate Definition 4.1 in terms of x-brackets 
Definition 5.2. A Hom-Lie H-conformal superalgebra is a triple 



1) Locality:

2) H-sesqui-linearity:

3) Skew-super commutativity:

4) Hom-super Jacobi identity:

where 



In the following we will show that there is a simple relationship between the x-bracket of a Hom-Lie H-con- formal superalgebra and the commutator in its annihilation Hom-Lie H-pseudo-superalgebra 

According to Proposition 4.2, we obtain
In other words,
Below we give one way of constructing Hom-modules over Hom-Lie H-pseudo-algebras, whose proofs are similar to that in [10] .
Proposition 5.3. Any Hom-module 



for all homogeneous elements 




condition: 


Conversely, any Hom-A(L)-module 

where 

6. Cohomology of Hom-Lie H-Pseudo-Superalgebras
In this section, we will consider the cohomology of Hom-Lie H-pseudo-superalgebras, generalizing the results of Hom-Lie H-pseudoalgebras and Lie superalgebras.
Let 





Explicitly, 
1) H-polylinearity: For any 


2) Skew-supersymmetry: For any

where 

The map 







For


where 





and for 

The fact that 



One can also modify the above definition by replacing everywhere 











In the following we will show that the cohomology theory of Hom-Lie H-pseudo-superalgebras describes extensions and deformations, just as any cohomology theory.
Theorem 6.1. Let 


of the Hom-Lie H-pseudo-superalgebra 


Proof. Let 





It is not hard to verify that 



Conversely, given an element of




Acknowledgements
The paper is partially supported by the Project Funded by China Postdoctoral Science Foundation (No. 2015M571725), the Key University Science Research Project of Anhui Province (Nos. KJ2015A294 and KJ2014A183) and the NSF of Chuzhou University (Nos. 2015qd01, 2014qd008 and 2014PY08).
Cite this paper
Shengxiang Wang,Tingting Tao, (2016) On Hom-Lie Pseudo-Superalgebras. Advances in Pure Mathematics,06,420-435. doi: 10.4236/apm.2016.66029
References
- 1. Bakalov, B., Kac, V.G. and Voronov, A.A. (1999) Cohomology of Conformal Algebras. Communications in Mathematical Physics, 200, 561-598.
http://dx.doi.org/10.1007/s002200050541 - 2. D’Andrea, A. and Kac, V.G. (1998) Structure Theory of Finite Conformal Algebras. Selecta Mathematica, 4, 377-418.
- 3. Kac, V.G. (1977) Lie Superalgebras. Advances in Mathematics, 26, 8-96.
http://dx.doi.org/10.1016/0001-8708(77)90017-2 - 4. Kac, V.G. (1998) Vertex Algebras for Beginners. 2nd Edition, American Mathematical Society, Providence.
http://dx.doi.org/10.1090/ulect/010 - 5. Kac, V.G. (1997) The Idea of Locality. In: Doebner, H.-D., et al., Eds., Physical Applications and Mathematical Aspects of Geometry, Groups and Algebras, World Scientific, Singapore, 16-32.
- 6. Kac, V.G. Formal Distribution Algebras and Conformal Algebras. XII-th International Congress in Mathematical Physics (ICMP’97), Brisbane, 8 April 1999, 80-97.
- 7. Yuan, L.M. (2014) Hom Gel’fand-Dorfman Bialgebras and Hom-Lie Conformal Algebra. Journal of Mathematical Physics, 55, Article ID: 043507.
http://dx.doi.org/10.1063/1.4870870 - 8. Yuan, L.M. (2016) A Lie Conformal Algebra of Block Type. arXiv, No. 1601.07388.
- 9. Borcherds, R.E. (1986) Vertex Algebras, Kac-Moody Algebras, and the Monster. Proceedings of the National Academy of Sciences of the United States of America, 83, 3068-3071.
http://dx.doi.org/10.1073/pnas.83.10.3068 - 10. Bakalov, B., D’Andrea, A. and Kac, V.G. (2001) Theory of Finite Pseudoalgebras. Advances in Mathematics, 162, 1-140.
http://dx.doi.org/10.1006/aima.2001.1993 - 11. Bakalov, B., D’Andrea, A. and Kac, V.G. (2006) Irreducible Modules over Finite Simple Lie Pseudoalgebras. I. Primitive Pseudoalgebras of Type W and S. Advances in Mathematics, 204, 278-346.
http://dx.doi.org/10.1016/j.aim.2005.07.003 - 12. Bakalov, B., D'Andrea, A. and Kac, V.G. (2013) Irreducible Modules over Finite Simple Lie Pseudoalgebras II. Primitive Pseudoalgebras of Type K. Advances in Mathematics, 232, 188-237. http://dx.doi.org/10.1016/j.aim.2012.09.012
- 13. Boyallian, C. and Liberati, J.I. (2012) On Pseudo-Bialgebras. Journal of Algebra, 372, 1-34.
http://dx.doi.org/10.1016/j.jalgebra.2012.08.009 - 14. Sun, Q.X. (2012) Generalization of H-Pseudoalgebraic Structures. Journal of Mathematical Physics, 53, Article ID: 012105.
http://dx.doi.org/10.1063/1.3665708 - 15. Hartwig, J., Larsson, D. and Silvestrov, S. (2006) Deformations of Lie Algebras Using σ-Derivations. Journal of Algebra, 295, 314-361.
http://dx.doi.org/10.1016/j.jalgebra.2005.07.036 - 16. Larsson, D. and Silvestrov, S. (2007) Quasi-Hom-Lie Algebras, Central Extensions and 2-Cocycle-Like Identities. Journal of Algebra, 288, 321-344.
http://dx.doi.org/10.1016/j.jalgebra.2005.02.032 - 17. Yau, D. (2009) Hom-Algebras and Homology. Journal of Lie Theory, 19, 409-421.
- 18. Yau, D. (2008) Enveloping Algebras of Hom-Lie Algebras. Journal of Generalized Lie Theory and Applications, 2, 95-108.
- 19. Yau, D. (2010) Hom-Bialgebras and Comodule Algebras. International Electronic Journal of Algebra, 8, 45-64.
- 20. Cheng, Y.S. and Yang, H.Y. (2010) Low-Dimensional Cohomology of q-deformed Heisenberg-Virasoro Algebra of Hom-Type. Frontiers of Mathematics in China, 5, 607-622.
http://dx.doi.org/10.1007/s11464-010-0063-z - 21. Sheng, Y.H. (2012) Representations of Hom-Lie Algebras. Algebras and Representation Theory, 15, 1081-1098.
http://dx.doi.org/10.1007/s10468-011-9280-8 - 22. Sheng, Y.H. and Bai, C.M. (2014) A New Approach to Hom-Lie Bialgebras. Journal of Algebra, 399, 232-250.
http://dx.doi.org/10.1016/j.jalgebra.2013.08.046 - 23. Yuan, L.M. (2012) Hom-Lie Color Algebra Structures. Communications in Algebra, 40, 575-592.
http://dx.doi.org/10.1080/00927872.2010.533726 - 24. Makhlouf, A. and Silvestrov, S. (2008) Hom-Algebra Structures. Journal of Generalized Lie Theory and Applications, 3, 51-64.
http://dx.doi.org/10.4303/jglta/S070206 - 25. Makhlouf, A. and Silvestrov, S. (2009) Hom-Lie Admissible Hom-Coalgebras and Hom-Hopf Algebras. In: Silvestrov, S., Paal, E., Abramov, V. and Stolin, A., Eds., Generalized Lie Theory in Mathematics, Physics and Beyond, Springer-Verlag, Berlin, 189-206.
- 26. Makhlouf, A. and Silvestrov, S. (2010) Hom-Algebras and Hom-Coalgebras. Journal of Algebra and Its Applications, 9, 553-589.
http://dx.doi.org/10.1142/S0219498810004117 - 27. Caenepeel, S. and Goyvaerts, I. (2012) Monoidal Hom-Hopf Algebras. Communications in Algebra, 40, 1933-1950.
- 28. Chen, Y.Y., Wang, Z.W. and Zhang, L.Y. (2013) The FRT-Type Theorem for the Hom-Long Equation. Communications in Algebra, 41, 3931-3948.
http://dx.doi.org/10.1080/00927872.2013.781614 - 29. Chen, Y.Y., Wang, Z.W. and Zhang, L.Y. (2014) Quasitriangular Hom-Hopf Algebras. Colloquium Mathematicum, 137, 67-88.
http://dx.doi.org/10.4064/cm137-1-5 - 30. Gohr, A. (2010) On Hom-Algebras with Surjective Twisting. Journal of Algebra, 324, 1483-1491.
http://dx.doi.org/10.1016/j.jalgebra.2010.05.003 - 31. You, M.M. and Wang, S.H. (2014) Constructing New Braided T-Categories over Monoidal Hom-Hopf Algebras. Journal of Mathematical Physics, 55, 111701.
http://dx.doi.org/10.1063/1.4900824 - 32. Zhang, X.H. and Wang, S.H. (2015) Weak Hom-Hopf Algebras and Their (Co)Representations. Journal of Geometry and Physics, 94, 50-71.
http://dx.doi.org/10.1016/j.geomphys.2014.11.014 - 33. Ammar, F. and Makhlouf, A. (2010) Hom-Lie Superalgebras and Hom-Lie Admissible Superalgebras. Journal of Algebra, 324, 1513-1528.
http://dx.doi.org/10.1016/j.jalgebra.2010.06.014 - 34. Scheunert, M. and Zhang, R.B. (1998) Cohomology of Lie Superalgebras and Their Generalizations. Journal of Mathematical Physics, 39, 5024-5061.
http://dx.doi.org/10.1063/1.532508 - 35. Sweedler, M.E. (1969) Hopf Algebras. Mathematics Lecture Notes Series. Benjamin, New York.
- 36. Bahturin, Y., Mikhalev, D., Zaicev, M. and Petrogradsky, V. (1992) Infinite Dimensional Lie Superalgebras. Walter de Gruyter Publisher, Berlin.
http://dx.doi.org/10.1515/9783110851205 - 37. Kassel, C. (1995) Quantum Groups. Graduate Texts in Mathematics. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-0783-2
NOTES
*Corresponding author.








































































