Received 4 December 2015; accepted 16 January 2016; published 19 January 2016

ABSTRACT

We study the following model: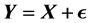. The aim is to estimate the distribution of X when only 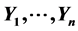are observed. In the classical model, the distribution of 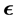is assumed to be known, and this is often considered as an important drawback of this simple model. Indeed, in most practical applications, the distribution of the errors cannot be perfectly known. In this paper, the author will construct wavelet estimators and analyze their asymptotic mean integrated squared error for additive noise models under certain dependent conditions, the strong mixing case, the b-mixing case and the r-mixing case. Under mild conditions on the family of wavelets, the estimator is shown to be 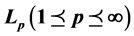-consistent and fast rates of convergence have been established.

Keywords:

Additive Noise, Density Estimation, Dependent Sequence, Rate of Convergence, Wavelet

1. Introduction

In practical situations, direct data are not always available. One of the classical models is described as follows:

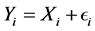
where 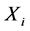stands for the random samples with unknown density 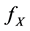and 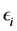denotes the i.i.d. random noise with density g. To estimate the density 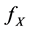is a deconvolution problem. Among the nonparametric methods of deconvolution, one can find estimation by model selection (e.g. Comte, Rozenhole and Taupin [1] ), wavelet thresholding (e.g. [2] ), kernel smoothing (e.g. Carroll and Hall, [3] ), spline deconvolution or spectral cut-off (e.g. Johannes [4] ) and Meister [5] basically on the effect of noise misspecification. However, a problem frequently encountered is that the proposed estimator is not everywhere positive, and therefore is not a valid probability density.

Sometimes, this problem can be circumvented by repeated observations of the same variable of interest, each time with an independent error. This is the model of panel data (see for example Li and Vuong [6] , Delaigle, Hall and Meister [7] , or Neumann [8] and references therein). On the other hand, there are many application fields where it is not possible to do repeated measurements of the same variable. So, information about the error distribution can be drawn from an additional experiment: a training set is used by experimenters to estimate the noise distribution. Think of 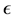as a measurement error due to the measuring device, then preliminary calibration measures can be obtained in the absence of any signal X (this is often called the instrument line shape of the measuring device).

Odiachi and Prieve [9] study the effect of additive noise in Total Internal Reflection Microscopy (TIRM) experiments. This is an optical technique for monitoring Brownian fluctuations in separation between a single microscopic sphere and a flat plate in aqueous medium. See Carroll and Hall [3] , Devroye [10] , Fan [11] , Liu and Taylor [12] , Masry [13] , Stefanski and Carroll [14] , Zhang [15] , Hesse [16] , Cator [17] , Delaigle and Gijbels [18] for mainly kernel methods and Koo [19] for a spline method, Efromovich [20] for particular strategy in supersmooth case and Meister (2004), on the effect of noise misspecification.

In this paper, we extend Geng and Wang [21] (Theorems 4.1 and 4.2) for certain dependent. More precisely, we prove that the linear wavelet estimator attains the standard rate of convergence i.e. the optimal one with additive noise for more realistic and standard dependent conditions as plynomial strong mixing dependence, the b-mixing dependence and r-mixing dependence. The properties of wavelet basis allow us to apply sharp probabilistic inequalities which improve the performance of the considered linear wavelet estimator.

The organization of the paper is as follows. Assumptions on the model are presented in Section 2. Section 3 is devoted to our linear wavelet estimator and a general result. Applications are set in Section 5, while technical proofs are collected in Section 6.

2. Estimation Procedure

The Fourier transform of 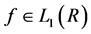is defined as follows:

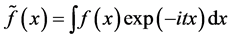
It is well known that 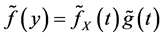for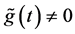. Let N be a positive integer. We assume that there exist constants 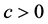and such that, for any x,

(1)

One can easily find an example

which is the Laplace density and, which satisfies (2.1) with.

We consider an orthonormal wavelet basis generated by dilations and translations of a father Daubechies-type wavelet and a mother Daubechies-type wavelet of the family db2N (see [22] ) Further details on wavelet theory can be found in Daubechies [22] and Meyer [23] . For any, we set and for, we define and as father and mother wavelet:

With appropriated treatments at the boundaries, there exists an integer such that, for any integer,

forms an orthonormal basis of. For any integer and, we have the following wavelet expansion:

where and. Furthermore we consider the following wavelet sequential definition of the Besov balls. We say, with, and if there exists a constant, such that

with the usual modifications if or. Note that, for particular choices of and contains the classical Holder and Sobolev balls. See, e.g., Meyer [23] and Hardle, Kerkyacharian, Picard and

Tsybakov [24] . We define the linear wavelet estimator by

(2)

where

(3)

(4)

Such an estimator is standard in nonparametric estimation via wavelets. For a survey on wavelet linear estimators in various density models, we refer to [25] . Note that by Plancherel formula, we have

In 1999, Pensky and Vidakovic [26] investigate Meyer wavelet estimation over Sobolev spaces and risk under moderately and severely ill-posed noises. Three years later, Fan and Koo [2] extend those works to Besov spaces, but the given estimator is not computable since it depends on an integral in the frequency domain that cannot be calculated in practice. It should be pointed out that, by using different method, Lounici and Nickl [27] study wavelet optimal estimation over Besov spaces and risk under both noises. In [3] , wavelet optimal estimation is provided over and risk under moderately ill-posed noise. Furthemore in 2014, Li and Liu [28] considered the wavelet estimation for random samples with moderately ill-posed noise.

Our work is related to the paper of Geng and Wang [21] , since our estimator is similar and we borrow a useful Lemma from that study. Geng and Wang [21] prove that, under mild conditions on the family of wavelets, the estimators are shown to be -consistent for additive noise model. We extend thier result to certain class of dependent observation and prove that the mean integrated squred error of linear wavelet estimator developed by [29] attains the standard rate of convergence i.e. the optimal one in the i.i.d. case.

3. Optimality Results

The main result of the paper is the upper bound for the mean integrated square error of the wavelet estimator, which is defined as usual by

We refer to [24] and [30] for a detailed coverage of wavelet theory in statistics. The asymptotic performance of our estimator is evaluated by determining an upper bound of the MISE over Besov balls. It is obtained as sharp as possible and coincides with the one related to the standard i.i.d. framework.

Theorem 3.1. Consider as Meyer scaling function, and in (2). We suppose

a) there exists constants and such that

(5)

b) for any, let be the joint distribution of, then there exists a constant such that

Let, with, , with. Then there exists a constant such that

Naturally, the rate of convergence in Theorem 4.1 is obtained to be as sharp as possible.

4. Applications

The three following subsections investigate separately the strong mixing case, the r-mixing case and the b-mixing case, which occur in a large variety of applications.

4.1. Application to the Strong Mixing Dependence

We define the m-th strong mixing coefficient of by

where is the s-algebra generated by the random variables (or vectors) and is the s-algebra generated by the random variables (or vectors). We say that is strong mixing if and only if.

Applications on strong mixing can be found in [15] [31] and [32] . Among various mixing conditions used in the literature, a-mixing has many practical applications. Many stochastic processes and time series are known to be a-mixing. Under certain weak assumptions autoregressive and more generally bilinear time series models are strongly mixing with exponential mixing coefficients. The a-mixing dependence is reasonably weak; it is satisfied by a wide variety of models including Markov chains, GARCH-type models and discretely observed discussions.

Proposition 4.1. Consider the strong mixing case as defined above. Suppose that there exist two constants, such that, for any integer m,

then

4.2. Application to the r-Mixing Dependence

Let be a strictly stationary random sequence. For any, we define the m―the maximal correlation coefficient of by r-mixing:

where is the s-algebra generated by the random variables (or vectors) and is the s- algebra generated by the random variables (or vectors). We say is r-mixing if and only if.

Proposition 4.2. Consider the r-mixing case as defined above. Furthermore, there exist two constants such that, for any integer m,

then

4.3. Application to the b-Mixing Dependence

Let be a strictly stationary random sequence. For any, we define the m-th b-mixing coefficient of by,

where the supremum is taken over all finite partitions and of, which are respectively, and are measurable, is the -algebra generated by and is the one generated by. We say that is b-mixing if and only if.

Full details can be found in e.g. [29] [31] [33] and [34] .

Proposition 4.3. Consider the b mixing case as defined above. Furthermore, there exist two constants such that, for any integer m,

then

5. Proofs

In this section, we investigate the results of Section 3 under the assumptions of Section 4.

Moreover, C denotes any constant that does not depend on l, k and n.

Proof of Theorem 3.1. Since we set, we have

Following the lines of Geng and Wang [21] , with Plancherel formula, it is easy to say is the unbiased estimation of, furthermore

(7)

where

and

(8)

on the other hand, it follows from the stationarity of that

(9)

where

For upper bound of, one can only consider the change of variables, and we obtain

By (6) and inequality obtained in Lemma 6 in [2] , we have,

Therefore

(10)

It follows from (5) that

(11)

Therefore, combining (7) to (11), we obtain

(12)

On the other hand, as we define and since for, , then there exists a constant, such that

(13)

It follows from (13) and (14) and the assumption on that

Now the proof of Theorem 3.1 is complete.

Proof of Proposition 5.1. We apply the Davydov inequality for strongly mixing processes (see [29] ); for any, we have

(14)

Since we have and

(15)

therefore

(16)

Now the proof is finished by (14), (15) and (16).

Proof of Proposition 5.2. Applying the covariance inequality for r-mixing processes (see Doukahn [32] ), we have

Hence by the same technique we use in (8), we obtain

Proof of Proposition 5.3. Since is b-mixing, for any bounded function g ([25] , equation line 12, p. 479 and Lemma 4.2 with) implies that

where b is a function such that. Following the lines of Geng and Wang [21] , we obtain

Cite this paper

N.Hosseinioun, (2016) Wavelet-Based Density Estimation in Presence of Additive Noise under Various Dependence Structures. Advances in Pure Mathematics,06,7-15. doi: 10.4236/apm.2016.61002

References