Advances in Pure Mathematics
Vol.05 No.11(2015), Article ID:59418,12 pages
10.4236/apm.2015.511060
A Series Approach to Perturbed Stochastic Volterra Equations of Convolution Type
Anna Karczewska, Bartosz Bandrowski
Faculty of Mathematics, Computer Science and Econometrics, University of Zielona Góra, Zielona Góra, Poland
Email: A.Karczewska@wmie.uz.zgora.pl
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 July 2015; accepted 4 September 2015; published 7 September 2015
ABSTRACT
In the paper, perturbed stochastic Volterra Equations with noise terms driven by series of independent scalar Wiener processes are considered. In the study, the resolvent approach to the equations under consideration is used. Sufficient conditions for the existence of strong solution to the class of perturbed stochastic Volterra Equations of convolution type are given. Regularity of stochastic convolution is supplied, as well.
Keywords:
Stochastic Linear Volterra Equation, Perturbed Equation, Strong Solution, Resolvent, Mild Solution, Stochastic Convolution, Series Approach

1. Introduction
Let 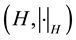 be a seperable Hilbert space and let
be a seperable Hilbert space and let 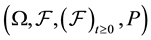 denote a probability space. We consider perturbed stochastic Volterra Equations in H of the form
denote a probability space. We consider perturbed stochastic Volterra Equations in H of the form
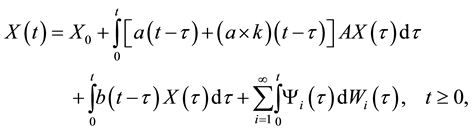 (1)
(1)
where  is an H-valued
is an H-valued  -measurable random variable, kernels a, k, b are real valued and locally inte- grable functions defined on
-measurable random variable, kernels a, k, b are real valued and locally inte- grable functions defined on  and A is a closed unbounded linear operator in H with a dense domain
and A is a closed unbounded linear operator in H with a dense domain .
.
The domain  is equipped with the graph norm
is equipped with the graph norm 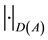 of A, i.e.
of A, i.e. .
.
In our work, the Equation (1) is driven by series of scalar Wiener processes;  and
and 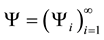 are appropriate processes defined below.
are appropriate processes defined below.
The goal of this paper is to formulate sufficient conditions for the existence and regularity of strong solutions to the perturbed Volterra Equation driven by series of scalar Wiener processes. Previously, in [1] - [4] , the stochastic integral for Hilbert-Schmidt operator-valued integrands and Wiener processes with values in Hilbert space has been constructed. Moreover, the particular series expansion of the Wiener process with respect to the eigenvectors of its covariance operator has been used. The stochastic integral used in this paper, originally introduced in [5] , bases on the construction directly in terms of the sequence of independent scalar processes. In consequence, the stochastic integral is independent of any covariance operator usually connected with a noise process.
In the paper, we use the resolvent approach to the Equation (1). This means that a deterministic counterpart of the Equation (1), that is, the Equation
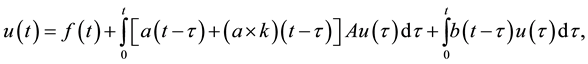 (2)
(2)
admits a resolvent family. In (2), the operator A and the kernel functions are the same as previously in (1) and f is a H-valued function.
By , we shall denote the family of resolvent operators corresponding to the Volterra Equation (2), which is defined as follows.
, we shall denote the family of resolvent operators corresponding to the Volterra Equation (2), which is defined as follows.
Definition 1 A family  of bounded linear operators in H is called resolvent for (2), if the following conditions are satisfied:
of bounded linear operators in H is called resolvent for (2), if the following conditions are satisfied:
1)  is strongly continuous on
is strongly continuous on 

2) 




3) the following resolvent equation holds

for all
In this paper, the following result concerning convergence of resolvents for the Equation (1) will play the key role.
As in [6] , we shall assume the following hypotheses:

is nonnegative, nonincreasing and convex.


Theorem 1 ( [6] , Th.~3.5) Assume that A is the generator of bounded analytic semigroup of H. Suppose that the hypotheses 







for all

Below we give an example illustrating conditions 

Example 1 Consider in the Equation (1) the following kernel functions
Then the functions
fulfil conditions 

The paper is organized as follows. Section 2 constains the construction of the stochastic integral due to O. van Gaans [5] . In Section 3, we compare mild and weak solutions and then we provide sufficient conditions for stochastic convolution to be a strong solution to the Equation (1). Section 4 gives regularity of stochastic con- volution arising in perturbed Volterra Equation while in Section 5 we derive the analogue of Itô formula to the perturbed Volterra Equation.
2. The Stochastic Integral
In this section we recall the construction of the stochastic integral due to O. van Gaans [5] .
Definition 2 A function 



Definition 3 A function 


Theorem 2 ( [5] ) Assume that 
pect to the filtration 


acting from 


1) For any


where
2) For each
3) For any

Definition 4 By 




Theorem 3 ( [5] ) Assume that 



exists in 
3. The Main Results
We begin this section with definitions of solutions to the Equation (1).
Definition 5 An h-valued predictable process





and for any 
Let 


Definition 6 An H-valued predictable process
and if for all 

As we have already written, in the paper we assume that (2) admits a resolvent family

Definition 7 An H-valued predictable process
and, for all

where 
We introduce the stochastic convolution

where 

Let us formulate some auxiliary results concerning the convolution
Proposition 4 For arbitrary process


Proposition 5 Assume that


For the idea of proofs of Propositions 4 and 5, we refer to [2] or [3] .
In some cases, weak solutions of Equation (1) coincides with mild solutions of (1), see e.g. [2] or [3] . In con- sequence, having results for the convolution (8) we obtain results for weak solutions.
Proposition 6 Assume that


Hence, we are able to conclude the following result.
Corollary 1 Let A be a linear bounded operator in H. If 

The formula (9) says that the convolution 
Here we provide sufficient conditions under which the stochastic convolution

Lemma 1 Assume that 


and
Proof Because 
exists in 
Denote by 




Theorem 7 Let A be a closed linear unbounded operator with the dense domain 
graph norm



Proof Since closed unbounded linear operator A becomes bounded in



It remains to show that the Equation (1) holds P − a.s., i.e.

Because the formula (9) holds for any bounded operator, then it holds for the Yosida approximation 
where
and
To prove that (11) holds, we need to show the following convergences

and

By assumption

deterministic and bounded for any




belongs to 



From the definition of stochastic integral (Theorem 3), for
By Theorem 1, the convergence of the resolvent families is uniform with respect to t on every closed intervals, particularly on

Summing up the above considerations, we obtain
as
From the fact that 



For any

Then
To prove that the convergence (13) holds, we need to show that

and

We shall study the term 

where 


Moreover

For any big enough n and any

Next, by Lemma 1 and closedness of the operator A
Analogously, we have
Using (19), we receive
From assumption


Then, using (19) and (12), we obtain (17).
For the term 
By assumption



Analogously,
Since


Using the convergence (20), we have
Therefore the convergence (18) holds. □
4. Continuity of Trajectories
In this section, we give sufficient conditions for the continuity of trajectories of the stochastic convolution when the kernel function

where
Theorem 8 Let the operator A be the generator of strongly continuous bounded analytic semigroup



dition 


where

like in Equation (1).
Proof Since formula (9) holds for any bounded operator, then it holds for the Yosida approximation 

where
Denoting

and using the Leibniz rule twice we obtain

From (23) and (24), we can write
If
and next
For simplicity, we introduce the following term
Then
Since
From (23) and (24) we obtain
where
Then
Basing on Theorem 1, properties of Yosida approximation 
and
Since the operator A is closed, we can conclude that
Hence, passing to the limit with
where

Lemma 2 Let the assumptions of Theorem 8 hold and


where

and
Moreover, 

Proof The formula (26) results from (22) and the definition (27) of the process

Using the Leibniz rule and property of semigroup we obtain
where
To conclude continuity of trajectories of stochastic convolution, we use regularity of solutions for the non- homogeneous Cauchy problem [7] to the formula (26).
Theorem 9 Suppose that the assumptions of Theorem 8 hold. If both processes Y and





In the previous theorem, the space


We denote by 










5. Analogue of the Itô Formula
In this section, we derive the analogue of the Itô formula to the perturbed Volterra Equation (1).
Proposition 10 Let the process X be a strong solution to the Equation (1) and






The following proposition is an example of application of the above analogue of the It formula.
Proposition 11 Let the operator A be the generator of bounded analytic semigroup in H. Suppose that 



Assume that the function 
1) function v and its partial derivatives

2) for any 
3) for any 
Then the stochastic convolution 
The idea of the proof bases on Ichikawa’s scheme, see ( [8] , Theorem 3.1), and on Theorem 1 and Proposition 10. It seems to be a good starting point in the study of stability of mild solution to perturbed Volterra Equation (1).
Cite this paper
Anna Karczewska,Bartosz Bandrowski, (2015) A Series Approach to Perturbed Stochastic Volterra Equations of Convolution Type. Advances in Pure Mathematics,05,660-671. doi: 10.4236/apm.2015.511060
References
- 1. Da Prato, G. and Zabczyk, J. (1992) Stochastic Equations in Infinite Dimensions. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511666223 - 2. Karczewska, A. (2007) Properties of Convolutions Arising in Stochastic Volterra Equations. International Journal of Contemporary Mathematical Sciences, 2, 1037-1051.
- 3. Karczewska, A. (2007) Convolution Type Stochastic Volterra Equations. Lecture Notes in Nonlinear Analysis. Juliusz Schauder Center for Nonlinear Studies. 10. Toruń.
- 4. Karczewska, A. and Lizama, C. (2009) Strong Solutions to Stochastic Volterra Equations. Journal of Mathematical Analysis and Applications, 349, 301-310.
http://dx.doi.org/10.1016/j.jmaa.2008.09.005 - 5. van Gaans, O. (2005) A Series Approach to Stochastic Differential Equations with Infinite Dimensional Noise. Integral Equations and Operator Theory, 51, 435-458.
http://dx.doi.org/10.1007/s00020-003-1258-4 - 6. Karczewska, A. and Lizama, C. (2014) Stochastic Volterra Equations under Perturbations. Electronic Communications in Probability, 19, 1-14.
http://dx.doi.org/10.1214/ECP.v19-3365 - 7. Da Prato, G. and Grisvard, P. (1979) Equations d’volution abstraites non linaires de type parabolique. Annali di Matematica Pura ed Applicata, 120, 329-396.
http://dx.doi.org/10.1007/BF02411952 - 8. Ichikawa, A. (1982) Stability of Semilinear Stochastic Evolution Equations. Journal of Mathematical Analysis and Applications, 90, 12-44.
http://dx.doi.org/10.1016/0022-247X(82)90041-5
























































