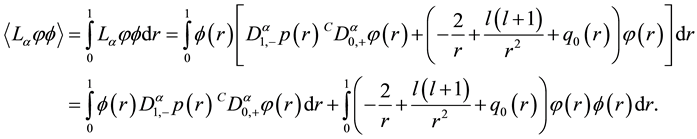Received 6 July 2015; accepted 6 November 2015; published 9 November 2015

ABSTRACT

In this paper, spectral analysis of fractional Sturm Liouville problem defined on (0, 1], having the singularity of type 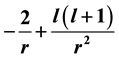at zero and researched the fundamental properties of the eigenfunctions and eigenvalues for the operator. We show that the eigenvalues and eigenfunctions of the problem are real and orthogonal, respectively.

Keywords:

Sturm-Liouville, Fractional, Hydrogen Atom, Singular, Spectral

1. Introduction

Fractional calculus have been available and applicable to various fields of science, the investigation of the theory of fractional differential equations has only been started recently. At the same time, fractional differential equations have great interest due to their numerous applications in many fields of science, such as physics, mechanics, chemistry, finance, electromagnetics, acoustics, viscoelasticity, electrochemistry, economy, etc. So far, there have been several fundamental works on the fractional derivative and fractional differential equations, written by Miller and Ross [1] Podlubny [2] Kilbas, Srivastava and Trujillo [3] .

In recent years, fractional Sturm-Liouville problems have been studied and these studies, which the eigenvalues and eigenfunctions associated to these operators and also theirs properties, have been published by M. Klimek and O. P. Argawal [4] [7] . Furthermore, there are a lot of studies in this topic [4] -[13] .

Sturm-Liouville problems have been studied for over two hundred years. The great progress has been made related to spectral theory. And this topic has an increasing interest for years from different points of view [14] - [23] .

2. Preliminaries

Firstly, we consider singular Sturm-Liouville equation

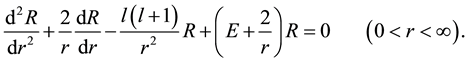
In quantum mechanics the study of the energy levels of the hydrogen atom leads to this equation [5] . Where R is the distance of the mass center to the origin. l is positive integer, a is real number E is energy constant and r is the distance between the nucleus with the electron.

Substitution 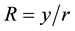reduces above equation to the form

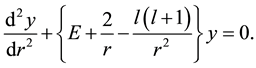
In most cases we took the reference potential to be

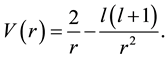
When 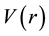is defined by last differential equation it contains a centripetal and Coulomb part, the usual singularities of the nuclear problem. We consider the following fractional singular Sturm-Liouville problem for hydrogen atom equation

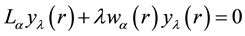
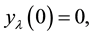
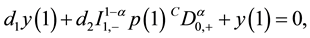
where the fractional order 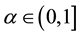and is defined as

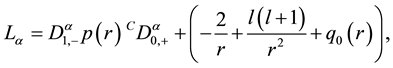
where 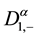and refers to the Riemann-Liouville and Caputo fractional derivative defined below by definition 2, respectively. The main theoretical result of the paper is prove spectral properties fractional singular Sturm-Liouville problem for hydrogen atom equation.

Definition 1. [2] Let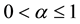. The left-sided and respectively right-sided Riemann-Liouville integrals of order are given by the formulas

(1)

(2)

where denotes the gamma function.

Definition 2. [2] Let . The left-sided and respectively right-sided Riemann-Liouville derivatives of order are defined as

(3)

(4)

Analogous formulas yield the left and right-sided Caputo derivatives of order:

(5)

(6)

Property 3. [7] The fractional differential operators defined in (3)-(6) satisfy the following identities:

(7)

(8)

Property 4. [7] Assume and. Then the following relations

(9)

hold for any . Furthermore, the integral operators defined in (1), (2) satisfy the following semi-group properties.

Now, let’s take up a fractional Sturm-Liouville problem for hydrogen atom equation.

3. A Singular Fractional Sturm-Liouville Problem for Hydrogen Atom Equation

Let’s denote a singular fractional Sturm-Liouville problem for hydrogen atom equation with the differential part containing the left and right-sided derivatives. Let’s use the form of the integration by parts formulas (7) and (8) for this new approximation. Main properties of eigenfunctions and eigenvalues in the theory of classical Sturm- Liouville problems are related to the integration by parts formula for the appear and the essential pairs are the left Riemann-Liouville derivative with the right Caputo derivative and the right Riemann-Liouville derivative with the left Caputo one.

Definition 5. For. Fractional hydrogen atom operator is written as

(10)

consider the fractional hydrogen atom equation

(11)

where and p, q are real valued continuous functions in interval (0, 1]. The boundary conditions for the operator L are the following:

(12)

(13)

where . The fractional boundary-value problem (11)-(13) is fractional Sturm-Liouville problem for hydrogen atom operator.

Theorem 6. Fractional hydrogen operator is self-adjoint on (0, 1].

Proof. Let us consider the following equation

Considering property 3 to the first integral in the last equation, we obtain the identity

(14)

Similarly, we obtain

(15)

The right hand sides of the Equations (14) and (15) are equal hence we may see that the left sides are equal that is

Therefore, The proof is completed.

Theorem 7. The eigenvalues of fractional hydrogen atom operator (11)-(13) are real.

Proof. Let us observe that following relation results from property (3)

(16)

Suppose that is the eigenvalue for (11)-(13) corresponding to eigenfunction y the following equalities are satisfy y and its complex conjugate

(17)

(18)

(19)

(20)

(21)

(22)

where We multiply Equation (17) by function and (20) by function y respectively and subtract:

Now, we integrate over interval (0, 1] and applying relation (16) we note that the right-hand side of the integrated equality contains only boundary terms:

by virtue of the boundary conditions (18), (19), (21), (22), we find

and because y is a non-trivial solution and , it easily seen that .

Theorem 8. The eigenfunctions corresponding to distinct eigenvalues of fractional hydrogen atom operator (11)-(13) are orthogonal weight function on (0, 1] that is

Proof. We have by assumptions fractional Sturm-Liouville for hydrogen atom operator fulfilled by two different eigenvalues and the respective eigenfunctions , in that case

(23)

(24)

(25)

(26)

(27)

(28)

we multiply Equation (23) by function and (26) by function respectively and subtract:

Integrating over interval (0, 1] and applying relation (16) we note that the right-hand side of the integrated equality contains only boundary terms:

Using the boundary conditions (24), (25), (27), (28), we find that

where . The proof is completed.

Cite this paper

ErdalBas,FundaMetin, (2015) Spectral Analysis for Fractional Hydrogen Atom Equation. Advances in Pure Mathematics,05,767-773. doi: 10.4236/apm.2015.513070

References