Advances in Pure Mathematics
Vol.05 No.09(2015), Article ID:57756,9 pages
10.4236/apm.2015.59049
Oscillating Statistics of Transitive Dynamics
Eleonora Catsigeras
Instituto de Matemática y Estadística “Rafael Laguardia”, Universidad de la República, Montevideo, Uruguay
Email: eleonora@fing.edu.uy
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 June 2015; accepted 3 July 2015; published 6 July 2015
ABSTRACT
We prove that topologically generic orbits of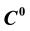 , transitive and non-uniquely ergodic dynamical systems, exhibit an extremely oscillating asymptotical statistics. Precisely, the minimum weak* compact set of invariant probabilities that describes the asymptotical statistics of each orbit of a residual set contains all the ergodic probabilities. If besides f is ergodic with respect to the Lebesgue measure, then also Lebesgue-almost all the orbits exhibit that kind of extremely oscillating statistics.
, transitive and non-uniquely ergodic dynamical systems, exhibit an extremely oscillating asymptotical statistics. Precisely, the minimum weak* compact set of invariant probabilities that describes the asymptotical statistics of each orbit of a residual set contains all the ergodic probabilities. If besides f is ergodic with respect to the Lebesgue measure, then also Lebesgue-almost all the orbits exhibit that kind of extremely oscillating statistics.
Keywords:
Measure Preserving Maps, Dynamical Systems, Ergodic Theory, Asymptotic Statistics

1. Introduction
We will study the statistical average for typical orbits of transitive dynamics, under a non traditional viewpoint.
On the one hand, the traditional viewpoint studies the limit in the future of the Birkhoff averages, starting always from the same initial point, and for Lebesgue-positive sets of orbits in the future. So, under this tradi- tional viewpoint, the “statistics” of the system (at least for C2-dynamical systems with some kind of hyperbo- licity), is mainly obtained from the existence of physical measures, of Sinai-Ruelle-Bowen (SRB) measures, and of Gibbs measures (see for instance the survey [3] ).
Relevant advances on the study of the asymptotic behavior of the time-averages from the traditional view- point can be found for instance in the following articles. In [8] Viana and Yang study the existence of physical measures for partially hyperbolic systems with one-dimensional center direction. Bonatti’s survey [2] gives an overview of the state of art in the theme of the asymptotical dynamics of C1-differentiable systems from the topological viewpoint. In [5] Liverani proves that piecewise C2 expanding maps may exhibit Gibbs measures without needing the bounded distortion property.
On the other hand, instead of adopting the traditional viewpoint, along this paper we will study the time averages that start at any future iterate of the initial point. This viewpoint is based on a philosophical argument: the way that the observers in the future will perceive the forward statistics of the system, is not the way that it is computed today. In fact, today the observers compute the Birkhoff average along the finite future piece orbit of length n (which we like to call “the clima”), by the mean value of the observable functions from time 0 to n. But the observers in the future―who will live, say, at time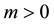 ―will compute their Birkhoff average along the finite piece of orbit of length n (i.e. they will perceive their clima), by the mean value of the observable functions between time m and time
―will compute their Birkhoff average along the finite piece of orbit of length n (i.e. they will perceive their clima), by the mean value of the observable functions between time m and time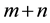 .
.
This non-traditional viewpoint of studying the Birkhoff averages and their limits (i.e. the statistics) does not give preferences to different initial observation instants. So, our conclusions include also the prediction of all the climas that the observers in the future will perceive.
The key result is Theorem 2:
Topologically typically, the clima observed at infinitely many times in the future must widely differ from the clima observed at present time, provided that the dynamics is deterministic (non hazardous), transitive and non- niquely ergodic.
This is an unexpected result, taking into account that the system is autonomous and deterministic. Nevertheless, the idea of the proof of Theorem 2 is extremely simple. The route of its proof is the result of join- ing the following three simple observations. First, if the system is transitive, then its topologically generic orbits in the future are dense. Second, for any ergodic measure , and for any
, and for any  -typical point
-typical point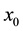 , the Birkhoff average starting at
, the Birkhoff average starting at 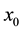 converges to
converges to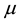 . So, for any
. So, for any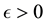 , for any fixed n sufficiently large, and for any point x close enough
, for any fixed n sufficiently large, and for any point x close enough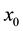 , the Birkhoff average starting at x is
, the Birkhoff average starting at x is 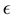 -near
-near . Third, any dense orbit in the future has such an iterate x close enough
. Third, any dense orbit in the future has such an iterate x close enough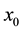 .
.
Thus, one concludes that the Birkhoff averages, with fixed n but starting at different points in the future of the same orbit, oscillate among all the ergodic measures of f, when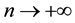 .
.
Even if the main theorem is the consequence of the latter simple observations, and no more proof than the above argument would be needed, we will include all the details of this proof (see Section 3) to be readable by a wide class of scientists and students.
1.1. Mathematical Background
Let M be a compact manifold of finite dimension. Let 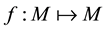 be continuous. We consider the dynamical system obtained by iteration of f in the future, i.e. the family of orbits
be continuous. We consider the dynamical system obtained by iteration of f in the future, i.e. the family of orbits 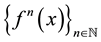 with initial condition
with initial condition

We denote by 


where 
Recall that a measure 




We recall that 
(See for instance Theorem 6.8 of [7] ).
To each initial state




where 





We agree to call the double-indexed sequence 
Since the space 


We agree to call the set of all limit probability measures of all such sequences of empirical probabilities in
1.2. Statement of the Results
If 

gent for Lebesgue-almost all 


In contrast, if instead of restricting to the case


Theorem 1. Let 
Let us state a similar result that holds for maps that do not preserve the Lebesgue measure. In Theorem 3.6 of
[1] , Abdenur and Andersson studied the limit set of the sequence 
orbits of C0-generic maps. Such generic systems do not preserve the Lebesgue measure. They proved that the
particular sequence 

Now, for transitive and non-uniquely systems, we observe all the sequences
instead of restricting to the case
Theorem 2. Let 
Theorems 1 and 2 imply the necessary extremely changeable “clima”, i.e. the time averages of the observable functions along finite pieces of all the relevant orbits in the ambient manifold M vary so much in the long term, to approach all the extremal invariant probabilities of the system (the ergodic measures). Even if the system is fully deterministic and it is governed by an autonomous and unchangeable recurrence equation, even if the parameters in this equation are fixed, even if the states along the deterministic orbit are not perturbed, no topologically relevant orbit of the system has a predictable statistics along its long-term future evolution. On the contrary, its asymptotical statistics is extremely changeable in the long-term future, exhibiting at least, as many probability distributions as ergodic measures of f exist.
This paper is organized as follows: In Section 2 we state the precise mathematical definitions to which the results refer, and in Section 3 we include the proofs of Theorems 1 and 2.
2. Definitions
Since the double-indexed sequence of empirical probabilities 

Definition 2.1. (Asymptotical statistics 
The asymptotical statistics of the orbit of





Following the classical Krylov-Bogolioubov construction of invariant probabilities (see for instance the proofs of Theorems 6.9, 6.10, and Corollary 6.9.1 of [7] ), it is standard to check that:
In other words, the asymptotical statistics of x is a nonempty compact set of probability measures which are invariant by f.
Definition 2.2. (Convergent or oscillating asymptotical statistics)
The orbit 
It is statistically oscillating if it is non convergent.
We recall that f is called uniquely ergodic if 
Definition 2.3. (Extremely oscillating asymptotical statistics)
When f is non-uniquely ergodic we say that the orbit 
Definition 2.4. (Transitive system) The dynamical system by iterates of 

Let us denote 

where 
Recall that M is a finite dimensional manifold. So, 

Definition 2.5. (Residual sets and generic orbits)
According to Baire-category theory a set 
Given a residual set 

3. The Proofs
The weak* topology of the space 

To prove Theorems 1 and 2 we first state the following lemmas:
Lemma 3.1. Let 





Proof: From equality (4), 
for some sequence 



Since




In other words, 


From equality (2) note that
Then
We have proved that, 


We conclude that

Lemma 3.2. If 


Proof: We take any continuous real function
From equality (3) we obtain
The last equality holds for all

Therefore, for


We conclude that
Now, it is left to prove that, for fixed




is continuous. So, let us prove that for any convergent sequence


To apply condition (1) we consider any continuous real function
Since 

We deduce that
From condition (1) we conclude the following equality in the space 
showing that the mapping 
To prove Theorem 1, we first state the following:
Lemma 3.3. Let 




Proof: Denote by m the Lebesgue measure of the manifold M, after a rescaling to make
From Lemma 3.2, for all 

Thus
Define

We conclude that 

But the set 
So, taking 
Note that if 




But the converse inclusion is obvious because for all

In brief, we have proved that
Substituting 
Finally, applying Lemma 3.1 we conclude
as wanted. ,
End of the proof of Theorem 1.
Proof: Fix 




of 






Since 

has total Lebesgue measure.
Take any




We deduce that

Since 
also has full Lebesgue measure. From (9) we have

We deduce that for Lebesgue-almost all

Since for any 


Applying Lemma 3.1, we deduce that



Now, to prove Theorem 2, we state the following:
Lemma 3.4. If 




Proof:
From Lemma 3.2, for all 
Consider the set 
Since f is continuous and transitive, from Definition 2.4 we obtain that, for any nonempty open set




So, taking 
Applying again Definition 2.5:
For all 


We deduce that
is also residual in M. In other words
Substituting 
Finally, applying Lemma 3.1 we conclude 
End of the proof of Theorem 2.
Proof: Fix 







Take any




Since 

We deduce that for generic

Since for any 


Applying Lemma 3.1, we deduce that



Acknowledgements
The author thanks the Editor and the anonymous Referee. She thanks the partial support of “Agencia Nacional de Investigación e Innovación” (ANII), “Comisión Sectorial de Investigación Cientfica” (CSIC) of “Universidad de la República”, and “Premio L’Oréal-UNESCO-DICYT” (the three institutions of Uruguay).
Cite this paper
EleonoraCatsigeras, (2015) Oscillating Statistics of Transitive Dynamics. Advances in Pure Mathematics,05,534-543. doi: 10.4236/apm.2015.59049
References
- 1. Abdenur, F. and Andersson, M. (2013) Ergodic Theory of Generic Continuous Maps. Communications in Mathematical Physics, 318, 831-855.
- 2. Bonatti, C. (2011) Towards a Global View of Dynamical Systems, for the C1-Topology. Ergod. Ergodic Theory and Dynamical Systems, 31, 959-993. http://dx.doi.org/10.1017/S0143385710000891
- 3. Buzzi, J. (2011) Chaos and Ergodic Theory. In: Meyers, R.A., Ed., Mathematics of Complexity and Dynamical Systems, Springer, New York, 63-87.
- 4. Catsigeras, E. and Enrich, H. (2011) SRB-Like Measures for C0 Dynamics. Bulletin of the Polish Academy of Sciences Mathematics, 59, 151-164. http://dx.doi.org/10.4064/ba59-2-5
- 5. Liverani, C. (2013) Multidimensional Expanding Maps with Singularities: A Pedestrian Approach. Ergodic Theory and Dynamical Systems, 33, 168-182. http://dx.doi.org/10.1017/S0143385711000939
- 6. Mañé, R. (1987) Ergodic Theory and Differentiable Dynamics. Springer-Verlag, New York.
- 7. Walters, P. (1982) An Introduction to Ergodic Theory. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-5775-2 - 8. Viana, M. and Yang, J. (2013) Physical Measures and Absolute Continuity for One-Dimensional Center Direction. Annales de l’Institut Henri Poincare (C) Non Linear Analysis, 30, 845-877.




















































