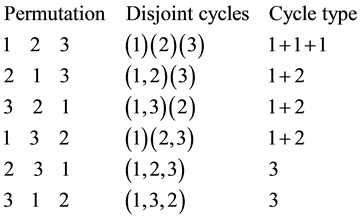Received 11 March 2015; accepted 26 May 2015; published 29 May 2015

ABSTRACT

The spectral properties of special matrices have been widely studied, because of their applications. We focus on permutation matrices over a finite field and, more concretely, we compute the minimal annihilating polynomial, and a set of linearly independent eigenvectors from the decomposition in disjoint cycles of the permutation naturally associated to the matrix.

Keywords:

Permutation Matrices, Eigenvalues, Eigenvectors

1. Introduction

As it is well known, permutations appear almost all in areas of mathematics. The study of permutation matrices has interest not only in matrix theory, but in other fields such as code theory, where they are a fundamental tool in construction of low-density parity-check codes (see [1] ).

Many properties are known of permutation matrices. In this work we focus on their spectral properties. More concretely, we obtain a formula for the minimal annihilating polynomial of a permutation matrix over a finite field and obtain a set of linearly independent eigenvectors of such a matrix.

Permutation matrices are orthogonal matrices, and therefore its set of eigenvalues is contained in the set of roots of unity. The product of permutation matrices is again a permutation matrix. They are invertible, and the inverse of a permutation matrix is again a permutation matrix. Permutation matrices are also double stochastic; in fact the set of doubly stochastic matrices corresponds to the convex hull of the set of permutation matrices (see [2] ). The characteristic polynomial of permutations matrices has also been studied (see, for example, [3] ).

Throughout the paper, we will denote by 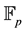the finite field of p elements (p is a prime number), and assume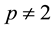. For any matrix, let us denote 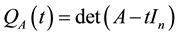the characteristic polynomial of A and by the minimal annihilating polynomial of A.

2. Preliminaries

Let us consider the set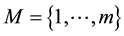. Any permutation 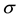of M can be written as a product of disjoint cycles (also called “orbits”). The usual notation 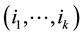of a k-cycle means that 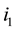is replaced 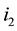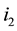by, by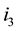, and so on being the last replacement 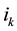by. A 1-cycle will be denoted by (i) and it means that this element remains unchanged (it is a fixed point of the permutation).

There is not an only possibility of the decomposition since being the cycles disjoint they can be written in any order and, moreover, any rotation of a given cycle specifies the same cycle.

See, for example, [4] and [5] for further reading about this topic.

A monomial matrix of order n is a regular -matrix which has in each row and in each column exactly one non-zero component. Permutation matrices are monomial matrices in which all non-zero components are equal to 1. Its rows are a permutation of the rows of the identity matrix. We will denote by 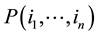the permutation matrix associated to the permutation of M,; that is to say, the permutation matrix in which the non-zero components are in columns. Equivalently, the permutation matrix in which the permutation applied to the rows of the identity matrix is. Another property of permutation matrices is given below.

The cycle type of a cycle is the data of how many cycles of each length are present in the cycle decomposition of the cycle. If the cycle is a product of -cycles, -cycles, ..., -cycles, then we will write that its cycle type is. Two permutations are conjugate in the symmetric group if and only if they have the same cycle type.

Example 1. We list below all the permutations of the symmetric group of n elements for, and, expressing the decomposition of the cycle in disjoint cycles and the cycle type. For, analogous tables can be constructed.

For:

For:

For:

2.1. Minimal Annihilating Polynomial of Permutation Matrices

The minimal annihilating polynomial of a permutation matrix can be deduced from the permutation to which the matrix is associated. In the case where the permutation considered is the identity it is obvious that.

In the non-trivial cases, the minimal annihilating polynomial can be determined by the decomposition of the permutation in disjoint cycles. This Section is devoted to prove this.

Lemma 1. Lep, be two permutation matrices associated to two permutations, with the same cycle type (conjugate in the symmetric group). Then the minimal annihilating polynomials and coincide.

Theorem 1. Let P be a permutation matrix associated to a permutation with cycle type . That is to say, let us assume that P is the permutation matrix associated to a permutation which is disjoint product of 1-cycles, 2-cycles, 3-cycles, ×××, r- cycles. Then

where if and if,.

Proof. Taking into account that any permutation is written as a product of disjoint cycles, we can deduce that the minimal annihilating polynomials for each of the matrices associated to these disjoint cycles. It is straightforward to check that the permutation matrix associated to a k-cycle is annihilated by the polynomial

and thus the statement follows.

Example 2. We list below the minimal annihilating polynomial of the permutation matrices associated to the permutations in the cases where. It is obvious that it depends only on the cycle-type of the cycle associated to the permutation matrix.

For:

For:

For:

2.2. Eigenvectors of Permutation Matrices

We will determine the set of eigenvectors of a permutation matrix from the decomposition of the permutation associated to it, in disjoint cycles. The proofs (not included) are based on straightforward computations.

Theorem 2. Let P be a permutation matrix associated to a permutation which is a disjoint product of cycles. Let us assume that one of them, has length k, and let be an eigenvalue of p, an kth-root of unity. Then the vector having in positions as coefficients is an eigenvector of P.

Illustrative examples

We will consider the case where in all the examples. Other cases can be handled analogously.

1. Let us consider the 2-cycle and the -matrix associated to it. Then the eigenvector for the eigenvalue, , is. Since the roots of are 1 and 4, there are two linearly independent eigenvectors: and.

2. If the permutation -matrix is associated to the 2-cycle, the eigenvector corresponding to the eigenvalue, , is. The equation has only one root, 1, and therefore there is an unique eigenvector is:.

If we consider the -permutation matrix is associated to the 2-cycle, there is also an unique eigenvector:.

3. Let us consider now the case of -permutation matrices associated to 4-cycles. Let be a 4th-root of unity (there are four 4th-roots of unity:, , and).

i) If the 4-cycle is, the eigenvector corresponding to the eigenvalue, is. That is to say, there are four linearly independent eigenvectors:

ii) If the 4-cycle is, the eigenvector corresponding to the eigenvalue, , is. That is to say, there are four linearly independent eigenvectors:

iii) If the 4-cycle is, the eigenvector corresponding to the eigenvalue, , is. That is to say, there are four linearly independent eigenvectors:

iv) If the 4-cycle is, the eigenvector corresponding to the eigenvalue, , is. That is to say, there are four linearly independent eigenvectors:

v) If the 4-cycle is, the eigenvector corresponding to the eigenvalue, , is. That is to say, there are four linearly independent eigenvectors:

vi) If the 4-cycle is, the eigenvector corresponding to the eigenvalue, , is. That is to say, there are four linearly independent eigenvectors:

4. Let us consider the permutation matrix associated to a cycle of type 2 + 2 + 4 + 8. Then the minimal annihilating polynomial is:. The eigenvalues in are:, , and, being the algebraic multiplicities 4,4,2,2, respectively.

Let us assume, for example, that the 2-cycles are: and, the 4-cycle is and the 8-cycle is. Then the following linearly independent eigenvectors are obtained.

3. Conclusion

We have found an easy way to write the minimal annihilating polynomial eigenvectors of a permutation matrix relating the permutation of its rows with its disjoint cycle decomposition. The results here can be generalized to monomial matrices, for example.

References