Advances in Pure Mathematics
Vol.05 No.02(2015), Article ID:53586,8 pages
10.4236/apm.2015.52008
A Note on the Structure of Affine Subspaces of
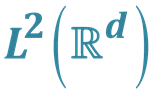
Fengying Zhou, Xiaoyong Xu
School of Science, East China Institute of Technology, Nanchang, China
Email: zhoufengying@ecit.cn, xxy@ecit.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 8 January 2015; accepted 26 January 2015; published 28 January 2015

ABSTRACT
This paper investigates the structure of general affine subspaces of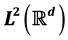 . For a d × d expansive matrix A, it shows that every affine subspace can be decomposed as an orthogonal sum of spaces each of which is generated by dilating some shift invariant space in this affine subspace, and every non-zero and non-reducing affine subspace is the orthogonal direct sum of a reducing subspace and a purely non-reducing subspace, and every affine subspace is the orthogonal direct sum of at most three purely non-reducing subspaces when |detA| = 2.
. For a d × d expansive matrix A, it shows that every affine subspace can be decomposed as an orthogonal sum of spaces each of which is generated by dilating some shift invariant space in this affine subspace, and every non-zero and non-reducing affine subspace is the orthogonal direct sum of a reducing subspace and a purely non-reducing subspace, and every affine subspace is the orthogonal direct sum of at most three purely non-reducing subspaces when |detA| = 2.
Keywords:
Affine Subspace, Reducing Subspace, Shift Invariant Subspace, Orthogonal Sum

1. Introduction
Let A be a d × d expansive matrix. Define the dilation operator D and the shift operator Tk,
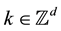 , by
, by
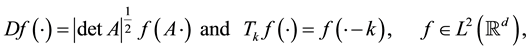
respectively. It is easy to check that they are both unitary operators on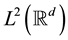 . Given a closed subspace X of
. Given a closed subspace X of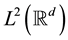 , X is called a shift invariant subspace if
, X is called a shift invariant subspace if
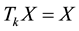 for every
for every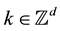 ; X is called a reducing subspace of
; X is called a reducing subspace of
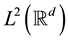 if
if
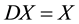 and
and
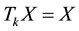 for every
for every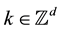 ; X is called an affine subspace of
; X is called an affine subspace of
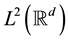 if there exists an at most countable subset
if there exists an at most countable subset
 of
of
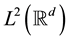 such that
such that
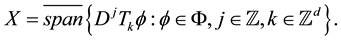
In this case, we say that



M. Therefore an affine subspace X of



2. Main Results
Lemma 1. Let X and Y be closed subspaces of a Hilbert space H and


1)
2)
Proof. 1) Obviously,
then
So

2) For














since
Lemma 2. Let


1) If

2) If

Proof. We only prove 1) since 2) can be obtained similarly. Since

If












The proof is completed.
Proposition 1. Suppose that X is an affine subspace of


in X such that the length of M1 is no more than that of M and
Proof. For each
Obviously,




[10] , we know that Y is a reducing subspace. Now define

Suppose that for some subset

Since





which shows that M1 is a shift invariant subspace of length no more than the length of M. The proof is completed.
Proposition 2. Suppose that X is a non-zero affine subspace of

1)


2)


Proof. 1): Obviously,



2): By 1) and Lemma 2, it follows that
If X is purely non-reducing, then














Proposition 3. Let X be an affine subspace of


Proof. We first show that



Next we will show that



So








Lemma 3. Let X and Y be affine subspaces of





Proof. Since


The proof is completed.
Lemma 4. Assume





Proof. Since













which shows that
Lemma 5. Let X be an affine subspace of


1)



2)


3)


Proof. 1): Note that we only need to show




2): Since Q is shift invariant and
If X is a reducing subspace, then



3): By 1) and 2), we have










Proposition 4. Let X and Y be affine subspaces of





Proof. Let M be a shift invariant subspace contained in







Proposition 5. Let X and Y be affine subspaces of


shift invariant subspaces contained in X and Y respectively. Define



Proof. According to Proposition 4,












Write



Hence
due to the fact that





So
Proposition 6. Let X and Y be two affine subspaces of


1)

2)



Proof. 1): By Lemma 5,




due to the facts that


Observe that




2): According to Proposition 5, it follows that
which shows that




Theorem 7. Let X be an affine subspace of
1) There exist a shift invariant subspace M in X such that




2) If X is a non-zero reducing subspace and

3) If X is non-zero and not reducing, then there exists a unique decomposition

4) If X is non-zero and
Proof. 1): By Proposition 1, it follows that












2): Let








Indeed, for









Then


Then
Obviously Q is a shift invariant subspace contained in X1 and
enough to show


Then for each
since



Hence
Thus
3): Let X be a non-reducing affine subspace of


4): 4) follows after 2) and 3). The proof is completed.
Acknowledgements
We thank the Editor and the referee for their comments. This work is funded by the National Natural Science Foundation of China (Grant No. 11326089), the Education Department Youth Science Foundation of Jiangxi Province (Grant No. GJJ14492) and PhD Research Startup Foundation of East China Institute of Technology (Grant No. DHBK2012205).
References
- Weiss, G. and Wilson, E.N. (2001) The Mathematical Theory of Wavelets. In: Byrnes, J.S., Ed., Twentieth Century Harmonic Analysis-A Celebration//Proceedings of the NATO Advanced Study Institute, Kluwer Academic Publishers, Dordrecht, 329-366.
- Dai, X., Diao, Y., Gu, Q. and Han, D. (2002) Frame Wavelets in Subspaces of
. Proceedings of the American Mathematical Society, 130, 3259-3267. http://dx.doi.org/10.1090/S0002-9939-02-06498-5
- Zhou, F.Y. and Li, Y.Z. (2010) Multivariate FMRAs and FMRA Frame Wavelets for Reducing Subspaces of
. Kyoto Journal of Mathematics, 50, 83-99. http://dx.doi.org/10.1215/0023608X-2009-006
- Dai, X., Diao, Y. and Gu, Q. (2002) Subspaces with Normalized Tight Frame Wavelets in
. Proceedings of the American Mathematical Society, 130, 1661-1667. http://dx.doi.org/10.1090/S0002-9939-01-06257-8
- Dai, X., Diao, Y., Gu, Q. and Han, D. (2003) The Existence of Subspace Wavelet Sets. Journal of Computational and Applied Mathematics, 155, 83-90. http://dx.doi.org/10.1016/S0377-0427(02)00893-2
- Lian, Q.F. and Li, Y.Z. (2007) Reducing Subspace Frame Multiresolution Analysis and Frame Wavelets. Communications on Pure and Applied Analysis, 6, 741-756. http://dx.doi.org/10.3934/cpaa.2007.6.741
- Li, Y.Z. and Zhou, F.Y. (2010) Affine and Quasi-Affine Dual Frames in Reducing Subspaces of
. Acta Mathematica Sinica (Chinese Edition), 53, 551-562.
- Gu, Q. and Han, D. (2009) Wavelet Frames for (Not Necessarily Reducing) Affine Subspaces. Applied and Computational Harmonic Analysis, 27, 47-54. http://dx.doi.org/10.1016/j.acha.2008.10.006
- Gu, Q. and Han, D. (2011) Wavelet Frames for (Not Necessarily Reducing) Affine Subspaces II: The Structure of Affine Subspaces. Journal of Functional Analysis, 260, 1615-1636. http://dx.doi.org/10.1016/j.jfa.2010.12.020
- Zhou, F.Y. and Li, Y.Z. (2013) A Note on Wavelet Frames for Affine Subspaces of
. Acta Mathematica Sinica (Chinese Edition), 33A, 89-97.





















































 . Proceedings of the American Mathematical Society, 130, 3259-3267.
. Proceedings of the American Mathematical Society, 130, 3259-3267.  . Kyoto Journal of Mathematics, 50, 83-99.
. Kyoto Journal of Mathematics, 50, 83-99.  . Proceedings of the American Mathematical Society, 130, 1661-1667.
. Proceedings of the American Mathematical Society, 130, 1661-1667.  . Acta Mathematica Sinica (Chinese Edition), 53, 551-562.
. Acta Mathematica Sinica (Chinese Edition), 53, 551-562. . Acta Mathematica Sinica (Chinese Edition), 33A, 89-97.
. Acta Mathematica Sinica (Chinese Edition), 33A, 89-97.