Received 9 November 2014; accepted 30 April 2015; published 6 May 2015

ABSTRACT

For a bounded linear operator A on a Hilbert space, let 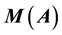be the smallest possible cons- tant in the inequality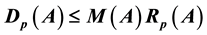. Here, p is a point on the smooth portion of the boundary 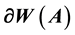of the numerical range of A. 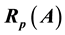is the radius of curvature of 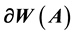at this point and is the distance from p to the spectrum of A. In this paper, we compute the 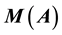for composition operators on Hardy space.

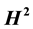Keywords:

Composition Operator, Numerical Range, Eigenvalues, Curvature

1. Introduction

For a bounded linear operator A on a Hilbert space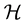, the numerical range 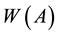is the image of the unit sphere of 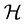under the quadratic form associated with the operator. More precisely,

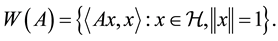
Thus the numerical range of an operator, like the spectrum, is a subset of the complex plane whose geometrical properties should say something about the operator.

One of the most fundamental properties of the numerical range is its convexity, stated by the famous Toeplitz-Hausdorff Theorem. Other important property of 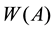is that its closure contains the spectrum of the operator, 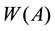is a connected set with a piecewise analytic boundary [1] .

Hence, for all but finitely many points, the radius of curvature of at p is well defined. By convention, if p is a corner point of, and if p lies inside a flat portion of.

Let denote the distance from p to, we define the smallest constant such that

(1)

for all with finite non-zero curvature.

By Donoghue’s theorem whenever. Therefore, for all convexoid element A. Recall that convexoid element is an element such that its numerical range coincides with the convex hull of its spectrum. For non-convexoid A,

(2)

where the supremum in the right-hand side is taken along all points with finite non-zero curvature.

The computation of for arbitrary matrix A is an interesting open problem. For, we do not have an exact value of. The question whether there exists a universal constant, posed by Mathias [2] . Caston, et al. [3] prove the following inequalities:

(3)

Mirman a sequence of Toeplitz nilpotent matrices with algrowing asymptotically as is also found [3] . Hence, the answer to Mathias question is negative. However, the lower bound in (3) is still of some interest, at least for small values of n. The question of the exact rate of growth of (it is, or n, or something in between) remains open.

2. Composition Operator on Hardy Space

Let denote the open unit disc in the complex plane, and the Hardy space H² the functions

holomorphic in such that, with denoting the n-th Taylor coefficient of f. The

inner product inducing the norm of is given by. The inner product of two functions f and g in may also be computed by integration:

where is positively oriented and f and g are defined a.e. on via radial limits.

For each holomorphic self map of induces on a composition operator defined by the equation. A consequence of a famous theorem of J. E. Littlewood [4] asserts that is a bounded operator. (see also [5] [6] ).

In fact (see [6] )

In the case, Joel H. Shapiro has been shown that the second inequality changes to equality if and only if is an inner function.

A conformal automorphism is a univalent holomorphic mapping of onto itself. Each such map is linear fractional, and can be represented as a product, where

for some fixed and (See [7] ).

The map interchanges the point p and the origin and it is a self-inverse automorphism of.

Each conformal automorphism is a bijection map from the sphere to itself with two fixed points (counting multiplicity). An automorphism is called:

Ÿ elliptic if it has one fixed point in the disc and one outside the closed disc;

Ÿ hyperbolic if it has two distinct fixed point on the boundary, and

Ÿ parabolic if there is one fixed point of multiplicity 2 on the boundary.

For, an r-dilation is a map of the form. We call r the dilation parameter of and in the case that, is called positive dilation. A conformal r-dilation is a map that is conformally conjugate to an -dilation, i.e., a map, where and is a conformal automorphism of.

For, an w-rotation is a map of the form. We call w the rotation parameter of. A straightforward calculation shows that every elliptic automorphism of must have the form

for some and some.

3. Main Results

In [8] , the shapes of the numerical range for composition operators induced on by some conformal automorphisms of the unit disc specially parabolic and hyperbolic are investigated.

In [9] , V. Matache determined the shapes in the case when the symbol of the composition operator the inducing functions are monomials or inner functions fixing 0. The numerical ranges of some compact composition operators are also presented.

Also, in [10] the spectrum of composition operators are investigated.

This facts will help in discussing and proving many of the results below.

Remark 3.1 If, , then and is a closed ellipticall disc whose boun-

dary is the ellipse of foci 0 and 1, having major/minor axis of length and. There- fore.

Remark 3.2 If, , then the closure of. If w is the n-th root

of unity then is the convex hull of all the n-th roots of unity and so. If w is not a root of

unity the is the union of and the set. In this case also.

Remark 3.3 If is hyperbolic with fixed point a, , then

and is a disc center at the origin. Therefore where is the numerical radius of.

Remark 3.4 If is parabolic, then and is a disc center at the origin. Therefore

.

Remark 3.5 If is elliptic with rotation parameter w, and w is not a root of unity, then and

is a disc center at the origin. Therefore.

Therefore we have the following table for.

Completing the Table

An elliptic automorphism of that does not fix the origin must have the form, where

for some fixed and If we wish to show this dependence of on p and w, we will denote the elliptic automorphism by.

If is periodic then, surprisingly, the situation seems even murkier: For period 2 has been shown the closure of is an elliptical disc with foci at (Corollary 4.4. of [8] ). It is easy to see that is open, also in [11] , the author completely determined for period 2.

Theorem 3.6 If is an elliptic automorphism with order 2 and P it’s only fixed point in open unit disc, then there is such that

Proof. Let the operator A be self-inverse, i.e., but, so is an ellipse with foci at ±1 [12] . If with. Then

If is an elliptic automorphism with order 2 and p it’s only fixed point in open unit disc, then

where. Since is a nontrivial self-inverse operator on Hardy space and is an inner

function, then

and so there is such that:

But for period then all we can say is that the numerical range of has k-fold symmetry and we strongly suspect that in this case the closure is not a disc. Because the numerical range in this case is an open problem, so the completing of is also open problem.

Acknowledgements

I thank the editor and the referee for their comments. Also, when the author is the responsible of establishing Center for Higher Education in Eghlid he is trying to write this paper, so I appreciate that center because of supporting me in conducting research.

References