Received 14 October 2014; revised 30 October 2014; accepted 14 November 2014

ABSTRACT

In the present paper, we obtain asymptotic expansion of the wavelet transform for large value of dilation parameter a by using López technique. Asymptotic expansion of Shannon wavelet, Morlet wavelet and Mexican Hat wavelet transform are obtained as special cases.

Keywords:

Asymptotic Expansion, Wavelet Transform, Mellin Convolution, Integral Transform

1. Introduction

The continuous wavelet transform of a function h with respect to the wavelet 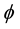is defined as

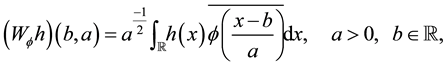(1)

provided the integral exists [1] . The asymptotic expansion for Mellin convolution

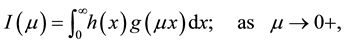(2)

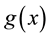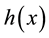was proposed by López [2] , under dyadic conditions on g and h. Let us remind earlier results from [2] , which will be used in present study. We assume that and have asymptotic expansions of the form:

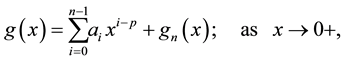(3)

and

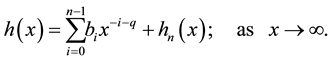(4)

Also assume that

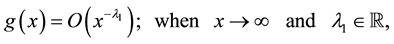(5)

and

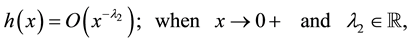(6)

with the parameters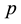, , 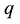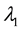and 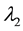satisfying the following conditions:

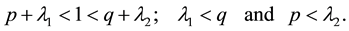(7)

The asymptotic expansion of (2) at the origin is given by the following Theorem ( [2] , pp. 631, 633, 634).

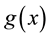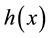Theorem 1 Assume that (i) and are locally integrable on; (ii) and have expansions of the form (3), (5) and (4), (6) respectively and (iii), , and satisfy (7), then the asym- ptotic expansion of (2) as are given by

Case I: For any and with, we have

(8)

Case II: For any and with, we have

(9)

Case III: For any and with, we have

(10)

By using Wong technique, the asymptotic expansions of wavelet transform (1) for large and small values of dilation parameters and translation, parameters were obtained by Pathak and Pathak 2009 [3] -[5] .

The main aim of the present paper is to derive asymptotic expansion of the wavelet transform for large value of a, by using Theorem 1. We also obtain asymptotic expansions for the special transforms corresponding to Shannon wavelet, Morlet wavelet and Mexican hat wavelet.

2. Asymptotic Expansion of the Wavelet Transform for Large Value of a

In this section, we obtain asymptotic expansion of the wavelet transform (1), when.

Now, let us rewrite (1) in the form:

(11)

where, and b is assumed to be a fixed real number.

Setting and assume that and are locally integrable on. Further as-

sume that and have asymptotic expansions of the form

(12)

(13)

Also assume that

(14)

and

(15)

with the parameters, , and satisfy the following condition

(16)

Then by using, Theorem 1, we obtain asymptotic expansion of for large value of a.

Case I: When and with, we have

(17)

Case II: When and with, we have

(18)

Case III: When and with, we have

(19)

Similarly, we can also obtain the asymptotic expansion of as.

3. Application

In this section, we apply the previous result and obtain the asymptotic expansions of Shannon wavelet transform, Morlet Wavelet transform and Mexican hat wavelet transform.

3.1. Asymptotic Expansion of the Shannon Wavelet Transform

Let us consider to be Shannon wavelet and it is given by [1] . Since, is lo-

cally integrable on and has the asymptotic expansion:

(20)

with

(21)

Consider, is locally integrable on and satisfies (13) and (15) with parameters

(22)

Now, by using (17), (18) and (19) respectively and by means of formula ([6] , p. 321, (41)), then the asymptotic expansions of Shannon wavelet transform are given by

Case I: When and, we get

(23)

Case II: When and, we get

(24)

Case III: When and, we get

(25)

3.2. Asymptotic Expansion of the Morlet Wavelet Transform

We choose to be Morlet wavelet and it is given by [1] . Since, is locally integrable on

and has the asymptotic expansion as

(26)

with

Let is locally integrable on and satisfy (13) and (15) with parameters (22). Now by using (17), (18) and (19) respectively and by formula ([6] , pp. 318, 320, (10,30)),then the asymptotic expansions of Morlet wavelet transform are given by

Case I: When and, we have

(27)

Case II: When and, we have

(28)

Case III: When and, we have

(29)

3.3. Asymptotic Expansion of the Mexican Hat Wavelet Transform

We choose to be Mexican hat wavelet [1] . Since is locally integrable on

and has the asymptotic expansion:

(30)

with

As is locally integrable on and satisfies (13) and (15) with parameters (22). Now by using (17), (18) and (19) respectively, we can obtain the asymptotic expansion of Mexican hat wavelet transform by using formula ([6] , p. 313, (13))

Case I: When and, we have

(31)

Case II: When and, we have

(32)

Case III: When and, we have

(33)

Acknowledgements

The authors are thankful to Prof. R. S. Pathak, DST Center for Interdisciplinary Mathematical Sciences, Banaras Hindu University, Varanasi-221005, India, for his valuable suggestion for the improvement of the article. We thank the referee for their comments. The research of the first author was supported by U.G.C-BSR start-up grant No. F.30-12/2014 (BSR).

References