Received 26 September 2014; revised 25 October 2014; accepted 31 October 2014

ABSTRACT

In this paper, based on the theories of α-times Integrated Cosine Function, we discuss the approximation theorem for α-times Integrated Cosine Function and conclude the approximation theorem of exponentially bounded α-times Integrated Cosine Function by the approximation theorem of n-times integrated semigroups. If the semigroups are equicontinuous at each point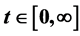, we give different methods to prove the theorem.

Keywords:

α-Times Integrated Cosine Function, Exponentially Bounded, Approximation

1. Introduction

Integrated semigroups were introduced by Arent [1] [2] and Davies and Pang [3] in 1987. The approximation theorem is one of the fundamental theorems in the theory of operater semigroups. There have been many results on approximation [4] - [7] . Cao [8] obtained the approximation theorem for m-times Integrated Cosine Function,. In this paper, we refine the theory by introducing α-times Integrated Cosine Function for positive real numbers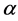. Moreover, if the semigroups are equicontinuous at each point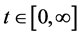, we give different methods to prove the theorem.

Throughout this paper, we will denote by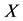—a Banach space with norm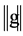, by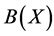—the Banach space of all bounded linear operators from 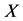to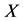; 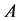is a linear operator in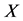, by

,

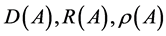respectively the domain, the range, the resolvent set, and the resolvent of.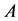

2. Preliminaries

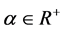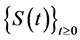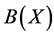Definition 2.1. Let, then a strongly continuous family in is called an -times Integrated Cosine Function, if the following hold:

1);

2) For any, and,

Definition 2.2. is a linear operator in, , is called the generator of an -times Integrated Cosine Function if there are nonnegative numbers and a mapping such that

1) is strongly continuous and for all;

2) is contained in the resolvent set of;

3) for.

Lemma 2.3. [9] For each let, with

and let

Assume that

and that for a fixed, , and

with uniform concergence for. Then exists.

Lemma 2.4. [10] If is a linear operator in,. The following assertions are equivalent:

1) There exist constant, such that, and

.

for，.

2), generate a -times Integrated Cosine Function, and exist constant such that -times Integrated Cosine Function hold

3. Main Results

Theorem 3.1. If generates a -times Integrated Cosine Function, and there is such that then the following statements are equivalent:

1), for some, and is equicontinuous at each point;

2), , and is equicontinuous at each point;

3), uniformly on compacts of.

Proof: 1) Þ 2) Consider the set

,

which is nonempty by assumption.

Let, then

when

Obviously converges as. Therefore, the set is open.

On the other hand, taking an accumulation point of with, we can find, such that. By the above considerations, must belong to, i.e., is relatively closed in, which leads to the conclusion.

2) Þ 3) Let

for

,

and is equicontinuous at each point; using Lemma 2.2, it is easy to know that exists. We now fix, then for each,; when, we have

(1)

Pick, then such that

(2)

From (1) (2), we have ，，.

It shows that 3) is right.

3) Þ 2) fix, for each, , when.

We have

,.

For is continuous on, then, , when

We have

，

Therefore, if，, then

In conclusion is equicontinuous at.

By using the dominated convergence theorem, we obtain

So 2) is right.

2) Þ 1) the proof is obvious.

The proof is completed.

Corollary 3.2. If is the generator of -times Integrated Cosine Function satisfying:

(3)

Then (1)-(3) are equivalent:

1)， for some.

2)，.

3)， uniformly on compacts of.

Theorem 3.3. If is the generator of -times Integrated Cosine Function, and there is such that , is equicontinuous at each point. exist, for some, , then there is a linear operator—ge- nerator of -times Integrated Cosine Function, such that, and uniformly on compacts of.

Proof: By, from the resolvent identity, we have

then hence and independent. Since, then there is a linear operator, ,.

By Definition 2.2, we know that

(4)

for exist, by the proof of the Theorem 3.1, we obtain that

exist,

hence,.

then generates a -times Integrated Cosine Function, such that, and uniformly on compacts of.

References