Advances in Pure Mathematics
Vol.4 No.7(2014), Article
ID:47617,8
pages
DOI:10.4236/apm.2014.47041
On the Norm of Elementary Operator
Denis Njue Kingangi1, John Ogoji Agure2, Fredrick Oluoch Nyamwala3
1Department of Mathematics and Computer Science, University of Eldoret, Eldoret, Kenya
2Department of Pure and Applied Mathematics, Maseno University, Maseno, Kenya
3Department of Physics, Mathematics, Statistics and Computer Science, Moi University, Eldoret, Kenya
Email: dankingangi2003@yahoo.com, johnagure@yahoo.com, foluoch2000@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2014; revised 20 May 2014; accepted 3 June 2014
ABSTRACT
The norm of an elementary operator has been studied by many mathematicians. Varied results have been established especially on the lower bound of this norm. Here, we attempt the same problem for finite dimensional operators.
Keywords:Bounded Linear Operator, Elementary Operator

1. Introduction
Let ![]() be a complex Hilbert space and
be a complex Hilbert space and  be the set of bounded operators on
be the set of bounded operators on![]() . A basic elementary operator,
. A basic elementary operator, 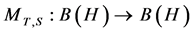 , is defined as:
, is defined as:
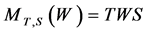 for
for 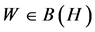 and
and ![]() fixed.
fixed.
An elementary operator, 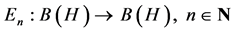 , is a finite sum of the basic elementary operators, defined as,
, is a finite sum of the basic elementary operators, defined as, 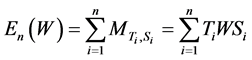 , for all
, for all , where
, where  are fixed, for
are fixed, for![]() .
.
When , we have
, we have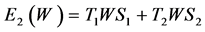 , for all
, for all  and
and 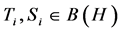 fixed, for
fixed, for ![]()
Given the elementary operator ![]() on
on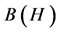 , the question on whether the equation
, the question on whether the equation
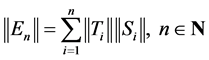 , holds remains an area of interest to many mathematicians. This paper attempts to answer this question for finite dimensional operators.
, holds remains an area of interest to many mathematicians. This paper attempts to answer this question for finite dimensional operators.
For a complex Hilbert space![]() , with dual
, with dual![]() , we define a finite rank operator
, we define a finite rank operator  by,
by, 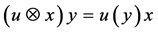 for all
for all![]() , where
, where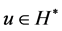 , and
, and ![]() is a unit vector, with:
is a unit vector, with:
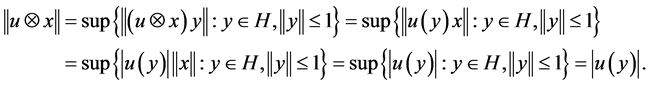
In this paper, we use finite rank operators to determine the norm of![]() . We first review some known results on the norm of the Jordan elementary operator
. We first review some known results on the norm of the Jordan elementary operator ,
, ![]() , for all
, for all  with
with 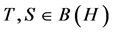 fixed. We will then proceed to show that for an operator
fixed. We will then proceed to show that for an operator 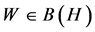 with
with 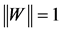 and
and  for all unit vectors
for all unit vectors![]() , then:
, then:
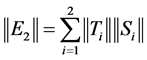 .
.
Some mathematicians have attempted to determine the norm of![]() . Timoney, used (matrix) numerical ranges and the tracial geometric mean to obtain an approximation of
. Timoney, used (matrix) numerical ranges and the tracial geometric mean to obtain an approximation of ![]() [1] , while Nyamwala and Agure used the spectral resolution theorem to calculate the norm of
[1] , while Nyamwala and Agure used the spectral resolution theorem to calculate the norm of ![]() induced by normal operators in a finite dimensional Hilbert space [2] .
induced by normal operators in a finite dimensional Hilbert space [2] .
The study of the norm of the Jordan elementary operator has also attracted many researchers in operator theory. Mathieu [3] , in 1990, proved that in the case of a prime C*-algebra, the lower bound of the norm of
 can be estimated by
can be estimated by 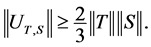 In 1994, Cabrera and Rodriguez [4] , showed that
In 1994, Cabrera and Rodriguez [4] , showed that  for prime JB*-algebras.
for prime JB*-algebras.
On their part, Stacho and Zalar [5] , in 1996 worked on the standard operator algebra which is a sub-algebra of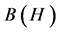 , that contains all finite rank operators. They first showed that the operator
, that contains all finite rank operators. They first showed that the operator 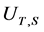 actually represents a Jordan triple structure of a C*-algebra. They also showed that if
actually represents a Jordan triple structure of a C*-algebra. They also showed that if 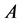 is a standard operator algebra acting on a Hilbert space
is a standard operator algebra acting on a Hilbert space![]() , and
, and![]() , then
, then 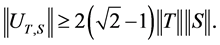 They later (1998), proved that
They later (1998), proved that
 for the algebra of symmetric operators acting on a Hilbert space. They attached a family of Hilbert spaces to standard operator algebra, using the inner products on them to obtain their results.
for the algebra of symmetric operators acting on a Hilbert space. They attached a family of Hilbert spaces to standard operator algebra, using the inner products on them to obtain their results.
In 2001, Barraa and Boumazguor [6] , used the concept of the maximal numerical range and finite rank operators to show that if 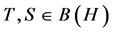 with
with![]() , then:
, then:
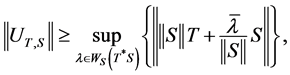
where,

is the maximal numerical range of 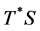 relative to
relative to ![]() , and
, and ![]() is the Hilbert adjoint of
is the Hilbert adjoint of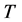 .
.
Okelo and Agure [7] used the finite rank operators to determine the norm of the basic elementary operator. Their work forms the basis of the results in this paper.
2. The Norm of Elementary Operator
In this section, we present some of the known results on elementary operators and proceed to determine norm of the elementary operator![]() .
.
In the following theorem Okelo and Agure [7] , determined the norm of the basic elementary operator.
Theorem 2.1 [5] : Let ![]() be a complex Hilbert space and
be a complex Hilbert space and  the algebra of bounded linear operators on
the algebra of bounded linear operators on![]() . Let
. Let 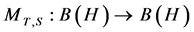 be defined by
be defined by 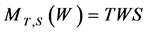 for all
for all 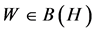 with
with ![]() as fixed elements in
as fixed elements in . If for all
. If for all 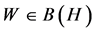 with
with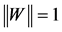 , we have
, we have 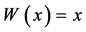 for all unit vectors
for all unit vectors![]() , then;
, then;
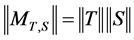 .
.
Proof: Since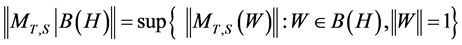 , we have,
, we have,![]() ;
;
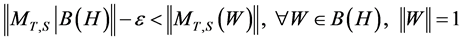
Therefore:
 .
.
Letting![]() , we obtain:
, we obtain:
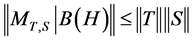 . (1)
. (1)
On the other hand, we have:
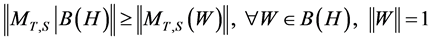 with:
with:
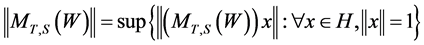 .
.
So, setting , and
, and , we have:
, we have:
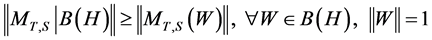 , with
, with ![]() fixed in
fixed in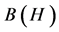 .
.
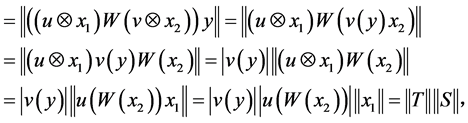
obtaining;
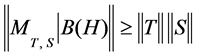 . (2)
. (2)
Hence, from (1) and (2), we obtain
 .
. 
For any vectors![]() , the rank one operator,
, the rank one operator, 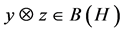 , is defined by
, is defined by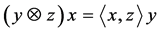 , for all
, for all![]() .
.
In the following three results Baraa and Boumazgour give three estimations to the lower bound of the norm of the Jordan elementary operator. See [6] . Recall that the Jordan elementary operator is the operator
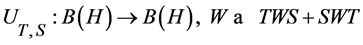 , for all
, for all 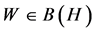 with
with 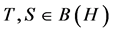 fixed.
fixed.
Theorem 2.2. Let 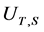 be the Jordan elementary operator with
be the Jordan elementary operator with  fixed, and with
fixed, and with![]() . Then
. Then
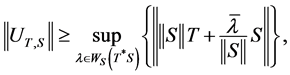
where, 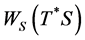 is the maximal numerical range of
is the maximal numerical range of 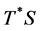 relative to
relative to![]() , as defined earlier.
, as defined earlier.
Proof: Let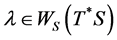 . Then there exists a sequence
. Then there exists a sequence 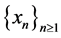 of unit vectors in
of unit vectors in ![]() such that
such that 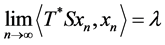 and
and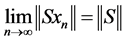 . Consider unit vectors
. Consider unit vectors![]() , and recall the rank one operator,
, and recall the rank one operator, 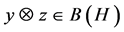 , defined as
, defined as , for all unit vectors
, for all unit vectors![]() . For fixed operators
. For fixed operators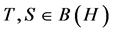 , we have;
, we have;

That is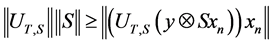 .
.
Thus we have:
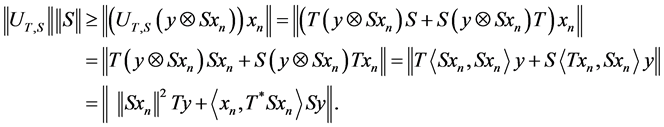
Hence
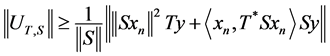 . (3)
. (3)
Letting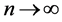 , we obtain:
, we obtain:
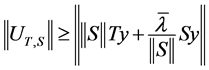 and this is true for any
and this is true for any , and for any unit vector
, and for any unit vector![]() .
.
Now, consider the set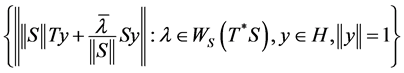 .
.
We have:

But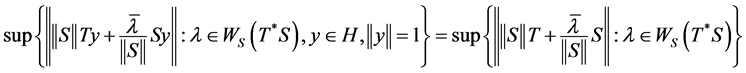 .
.
Therefore:
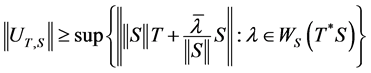 and this completes the proof.
and this completes the proof. 
Corollary 2.3: Let ![]() be a complex Hilbert space and
be a complex Hilbert space and ![]() be bounded linear operators on
be bounded linear operators on![]() . Let
. Let
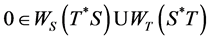 . Then we have
. Then we have 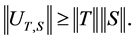
Proof: Let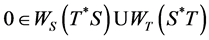 . Then ,
. Then ,  or
or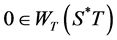 , and therefore, either there is a sequence
, and therefore, either there is a sequence 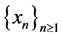 of unit vectors in
of unit vectors in ![]() such that
such that 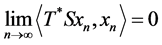 and
and 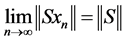 or, there is a sequence
or, there is a sequence 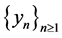 of unit vectors in
of unit vectors in ![]() such that
such that 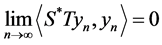 and
and .
.
Recall that in the previous theorem (Inequality (3)), we obtained:

This is equivalent to:
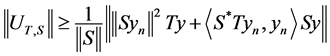 , (4)
, (4)
considering the sequence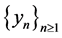 Taking limits in either (3) or (4), we obtain
Taking limits in either (3) or (4), we obtain
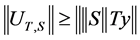 and this is true for any unit vector
and this is true for any unit vector![]() .
.
Now, consider the set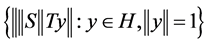 .
.
We have:
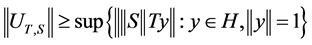 .
.
But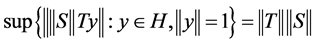 .
.
Therefore:
 and this completes the proof.
and this completes the proof. 
Proposition 2.4: Let ![]() be a complex Hilbert space and
be a complex Hilbert space and ![]() be bounded linear operators on
be bounded linear operators on![]() . If
. If
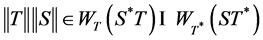 then:
then:
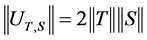 .
.
Proof: Suppose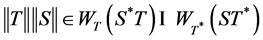 . Then
. Then 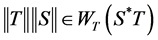 and
and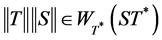 , and therefore we can find two sequences
, and therefore we can find two sequences 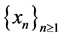 and
and 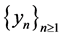 of unit vectors in
of unit vectors in ![]() such that:
such that:
 ,
, 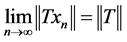 and
and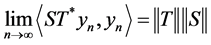 ,
,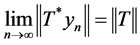 .
.
Since 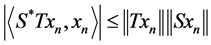 and
and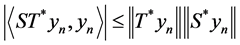 , then
, then 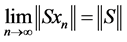 and
and
 .
.
For each![]() , we have:
, we have:
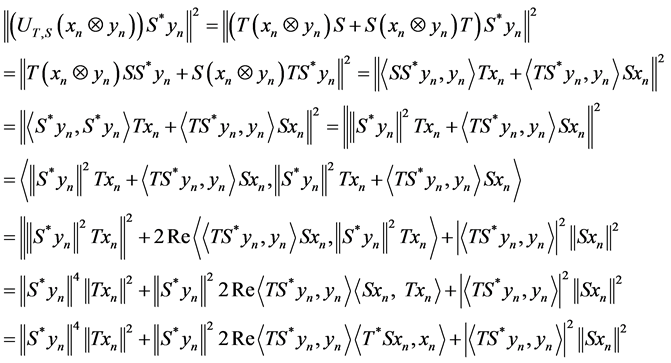
Now, we have:
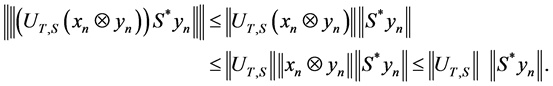
Therefore:
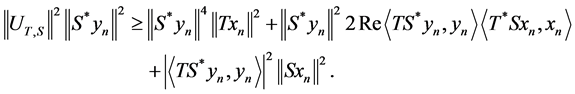
Letting  we obtain:
we obtain:

That is 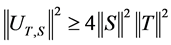 and this implies that
and this implies that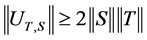 .
.
Clearly, 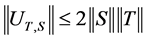 and therefore we obtain
and therefore we obtain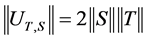 .
. 
We recall that an elementary operator, 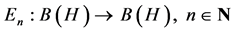 , is defined as
, is defined as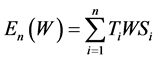 , for all
, for all  where
where 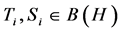 are fixed, for
are fixed, for![]() . When
. When![]() , we have
, we have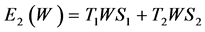 , for all
, for all  and
and  fixed, for
fixed, for ![]()
The following result gives the norm of![]() .
.
Theorem 2.5: Let ![]() be a complex Hilbert space and
be a complex Hilbert space and  be the algebra of all bounded linear operators on
be the algebra of all bounded linear operators on![]() : Let
: Let ![]() be the elementary operator on
be the elementary operator on 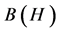 defined above. If for an operator
defined above. If for an operator 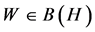 with
with , we have
, we have 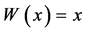 for all unit vectors
for all unit vectors![]() , then:
, then:
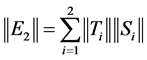 .
.
Proof: Recall that 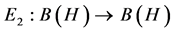 is defined as
is defined as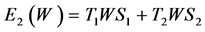 , for all
, for all 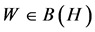 and
and 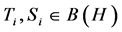 fixed, for
fixed, for ![]()
We have:
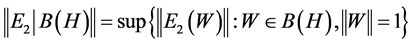 .
.
Therefore, 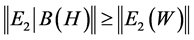 for all
for all 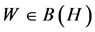 with
with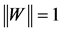 .
.
So, for all![]() ,
, 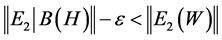 for all
for all  with
with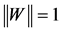 .
.
Therefore,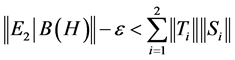 .
.
Letting![]() , we obtain:
, we obtain:
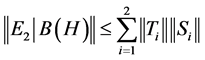 . (5)
. (5)
Next, we show that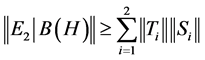 .
.
Since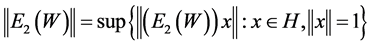 , then we have
, then we have 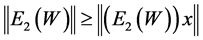 for all
for all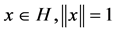 . But
. But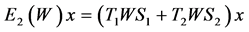 .
.
Now, let 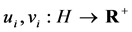 be functionals for
be functionals for ![]()
Choose unit vectors ![]() and define finite rank operators
and define finite rank operators 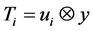 and
and 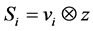 on
on![]() , for
, for ![]() by
by 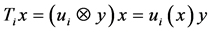 for all
for all ![]() with
with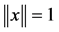 , for
, for![]() , and
, and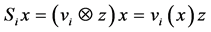 , for
, for ![]() with
with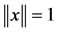 , for
, for![]() .
.
Observe that the norm of 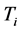 for
for ![]() is,
is,
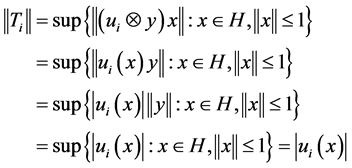
That is 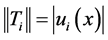 for any unit vector
for any unit vector ![]() with
with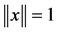 , for
, for![]() .
.
Likewise, the norm of  is
is 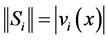 for any unit vector
for any unit vector ![]() with
with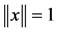 , for
, for![]() .
.
Therefore, for all ![]() with
with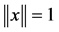 , we have
, we have
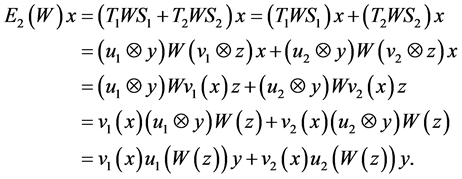
Since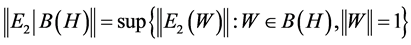 , we have:
, we have:

Now, since 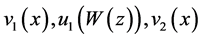 and
and 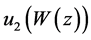 are all positive real numbers, we have
are all positive real numbers, we have
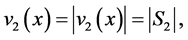

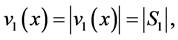 and
and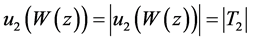 .
.
Thus 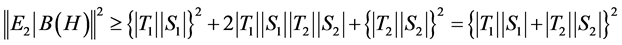 and hence we have
and hence we have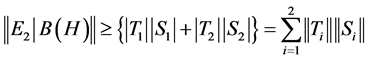 .
.
That is,
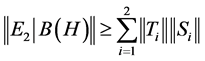 . (6)
. (6)
Now, (5) and (6) implies that:
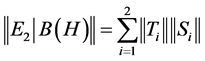 and this completes the proof.
and this completes the proof. 
References
- Timoney, R.M. (2007) Some Formulae for Norms of Elementary Operators. The Journal of Operator Theory, 57, 121-145.
- Nyamwala, F.O. and Agure, J.O. (2008) Norms of Elementary Operators in Banach Algebras. Journal of Mathematical Analysis, 2, 411-424.
- Mathew, M. (1990) More Properties of the Product of Two Derivations of a C*-Algebras. Bulletin of the Australian Mathematical Society, 42, 115-120. http://dx.doi.org/10.1017/S0004972700028203
- Cabrera, M. and Rodriguez, A. (1994) Non-Degenerate Ultraprime Jordan-Banach Algebras: A Zelmano-Rian Treatment. Proceedings of the London Mathematical Society, 69, 576-604.
- Stacho, L.L. and Zalar, B. (1996) On the Norm of Jordan Elementary Operators in Standard Operator Algebras. Publicationes Mathematicae-Debrecen, 49, 127-134.
- Baraa, M. and Boumazgour, M. (2001) A Lower Bound of the Norm of the Operator . Extracta Mathematicae, 16, 223-227.
- Okelo, N. and Agure, J.O. (2011) A Two-Sided Multiplication Operator Norm. General Mathematics Notes, 2, 18-23.

