Advances in Pure Mathematics
Vol.4 No.5(2014), Article ID:45618,5 pages DOI:10.4236/apm.2014.45022
β-Hausdorff Operator on Lipschitz Space in the Unit Polydisk*
Rong Hu, Chaofeng Zhang#
School of Mathematics and Finance-Economics, Sichuan University of Arts and Science, Dazhou, China
Email: #zbeyondiee@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 27 February 2014; revised 27 March 2014; accepted 2 April 2014
ABSTRACT
In this paper, we define β-Hausdorff operator on the unit polydisk and study the boundedness of the operator on Lipschitz space. Firstly, we translate the problem of coefficient into integral of weighted composition operator, then give the sufficient conditions of boundedness, and also obtain an upper bound for the operator norm on Lipschitz space.
Keywords:Unit Polydisk, Lipschitz Space, β-Hausdorff Operator, Weighted Composition Operator

1. Introduction
Let 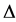 be the forward difference operator defined on sequences
be the forward difference operator defined on sequences 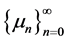 by
by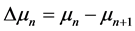 . Let operator
. Let operator be
be

Define the  -Hausdorff matrix
-Hausdorff matrix 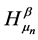 as the lower triangular matrix
as the lower triangular matrix 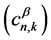 with entries
with entries

For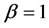 , it is the Hausdorff matrix
, it is the Hausdorff matrix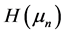 , see [1] .
, see [1] .
When 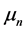 is the moment sequence of a measure i.e.
is the moment sequence of a measure i.e.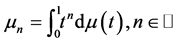 , the matrix arising from a Borel measure
, the matrix arising from a Borel measure  is denoted by
is denoted by , a simple calculation then gives
, a simple calculation then gives
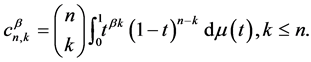
Let 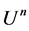 be the unit polydisk in the complex vector space
be the unit polydisk in the complex vector space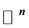 ,
, 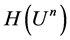 be the space of all holomorphic functions on
be the space of all holomorphic functions on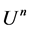 , and
, and  be the Borel measures on
be the Borel measures on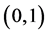 ,
,  ,
, .
.
In [2] , the Lipschitz space 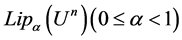 is defined on
is defined on 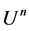 by
by
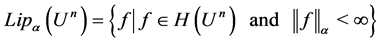
where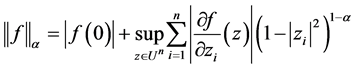 . It is easy to prove that
. It is easy to prove that 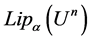 is a Banach space under the norm
is a Banach space under the norm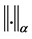 .
.
Let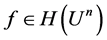 , suppose
, suppose , and
, and  be the
be the  - Hausdorff matrices arising by Borel measures
- Hausdorff matrices arising by Borel measures . The
. The 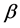 -Hausdorff operator
-Hausdorff operator 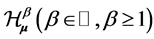 is defined as follows:
is defined as follows: . For
. For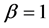 , we obtain the classical Hausdorff operator
, we obtain the classical Hausdorff operator , see [3] .
, see [3] .
Hausdorff matrix and Hausdorff operator have studied on various space of holomorphic functions, see, e.g., [3] -[9] . In [3] , the author obtained that the Hausdorff operator 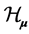 is bounded on Hardy space
is bounded on Hardy space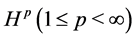 , and in [4] we showed that this conclusion cannot be extended to the Bloch space directly. Then we try to study on the Lipschitz space, found that when the measure is common Lebesgue measure
, and in [4] we showed that this conclusion cannot be extended to the Bloch space directly. Then we try to study on the Lipschitz space, found that when the measure is common Lebesgue measure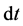 , the Hausdorff operator
, the Hausdorff operator  is unbounded on Lipschitz space
is unbounded on Lipschitz space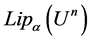 , see the remark. In this paper, we study the operator which is got by amending the Hausdorff operator and called it
, see the remark. In this paper, we study the operator which is got by amending the Hausdorff operator and called it 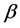 -Hausdorff operator. The results of this paper can be deemed as a continuation of the results in [3] on Lipschitz space.
-Hausdorff operator. The results of this paper can be deemed as a continuation of the results in [3] on Lipschitz space.
2. Main Results
The main results in this paper is the following:
Theorem 1 Let  be finite Borel measures on (0,1) and
be finite Borel measures on (0,1) and 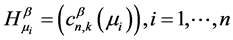 be corresponding
be corresponding  -Hausdorff matrices,
-Hausdorff matrices, 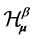 be
be 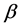 -Hausdorff operator. For
-Hausdorff operator. For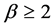 ,
, 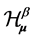 is bounded on
is bounded on 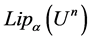 if
if
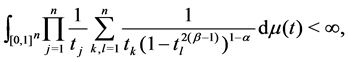
In this case, the operator norm satisfies
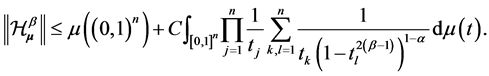
for some constant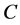 .
.
In order to prove the main results, we need some auxiliary result.
Lemma 1 [2] Let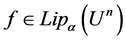 ,then
,then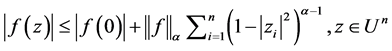 .
.
For each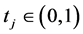 , we note the functions
, we note the functions 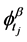 given by
given by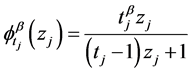 Lemma 2 Let
Lemma 2 Let  be finite Borel measures on
be finite Borel measures on  and
and 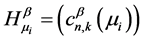 be corresponding
be corresponding 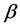 -Hausdorff matrices. Suppose
-Hausdorff matrices. Suppose

Then(a) The power series 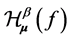 in (2) represents a holomorphic functions on
in (2) represents a holomorphic functions on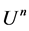 ;
;
(b) 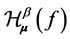 can be written in terms of weighted composition operators as follows:
can be written in terms of weighted composition operators as follows:
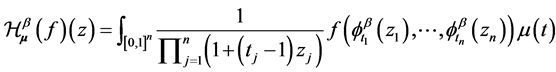 . For each
. For each .
.
Proof (a) Let . Since
. Since  the sequence of Taylor coefficients of
the sequence of Taylor coefficients of  is bounded by a constant
is bounded by a constant , then
, then

Hence the coefficients of the series (2) are bounded and consequently 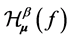 is defined and analytic on
is defined and analytic on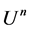 .
.
(b) By the Schwarz lemma we have  for each
for each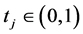 . Hence applying (3) we have
. Hence applying (3) we have
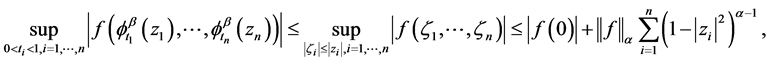
On the other hand,
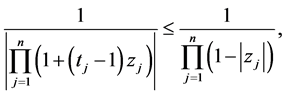
Hence

is finite and analytic on .
.
Now we proof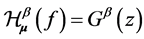 , in order to avoid tedious calculations, we may assume that
, in order to avoid tedious calculations, we may assume that , For a fixed
, For a fixed 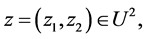 we have
we have
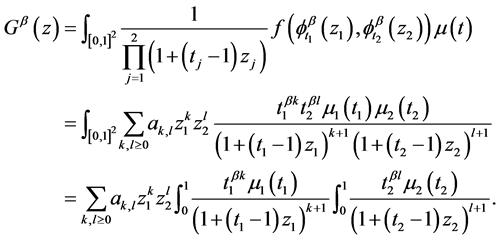
It easy to see that
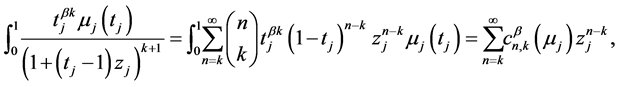
Hence,
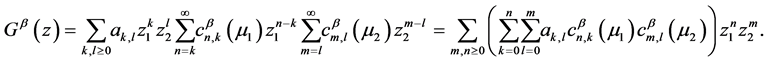
Denote 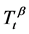 as follows
as follows

where 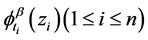 is defined in (4).
is defined in (4).
Now we obtain estimates for the norms of the weighted composition operator 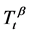 .
.
Lemma 3 Suppose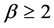 , then
, then 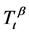 is bounded on
is bounded on . Further more, there is a constant
. Further more, there is a constant 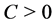
such that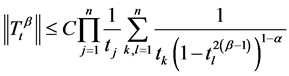 . For each
. For each .
.
Proof Let , in which
, in which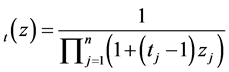 ,
, 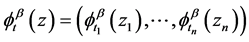 and the function
and the function  is defined in (4).
is defined in (4).

and . Hence we obtain that
. Hence we obtain that
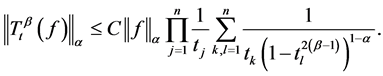
Now we proof the main results.
The Proof of Theorem 1 For each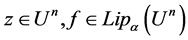 , by (5) we can obtain
, by (5) we can obtain

Then by (1) and (6),
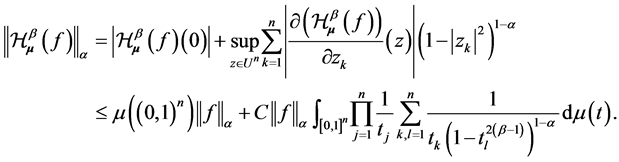
from which the result follows.
Remark When the Borel measure  is the common Lebesgue measure
is the common Lebesgue measure , the Hausdorff operator arising from measure
, the Hausdorff operator arising from measure  is denoted as
is denoted as .
. 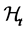 is bounded on Hardy space
is bounded on Hardy space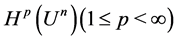 , see [3] .
, see [3] .
However, it is unbounded on Lipschitz space. For example, fix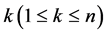 , and let
, and let , it is easy to see that
, it is easy to see that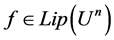 , then
, then
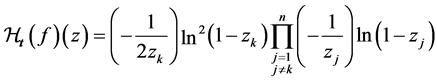
From this it follows that
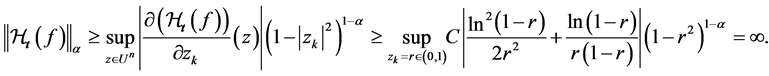
References
- Garabedian, H.L. (1939) Hausdorff Matrices. The American Mathematical Monthly, 46, 390-410. http://dx.doi.org/10.2307/2303033
- Zhou, Z.H. (2003) Composition Operators on the Lipschitz Space in Polydiscs. Science in China, 46, 33-38. http://dx.doi.org/10.1360/03ys9004
- Chang, D.C., Gilbert, R. and Stević, S. (2006) Hausdorff Operator on the Unit Polydisk in
 . Complex Variables and Elliptic Equations, 4, 329-345. http://dx.doi.org/10.1080/17476930600610528
. Complex Variables and Elliptic Equations, 4, 329-345. http://dx.doi.org/10.1080/17476930600610528 - Hu R., Xie L. and Hu, P.Y. (2012) Hausdorff-Type Operator on Bloch Space in the Unit Polydisk in
 . Acta Mathematica Scientia, 32, 521-529.
. Acta Mathematica Scientia, 32, 521-529. - Timoney, R.M. (1980) Blochfunctions in Several Complex Variables. Bull London Math, 319, 1-22.
- Zhou, Z.H. and Wei, Z.Q. (2005) Weighted Composition Operators on the Bloch Space in Polydiscs. Journal of Mathematics, 25, 435-440
- Galanopoulos, P. and Siskakis, A. (2001) Hausdorff Matrices and Composition Operators. Illinois Hournal of Math, 45, 757-773.
- Liflyand, E. and Móricz, F. (2000) The Hausdorff Operator Is Bounded on the Real Hardy Space. Proceedings of the American Mathematical Society, 128, 1391-1396. http://dx.doi.org/10.1090/S0002-9939-99-05159-X
NOTES

*This work is Supported by the Sichuan Provincial Natural Science Foundation (13ZB0101,13ZB0102).
#Corresponding author.

