Advances in Pure Mathematics
Vol.4 No.6(2014), Article
ID:46584,8
pages
DOI:10.4236/apm.2014.46031
A Solution of Generalized Cosine Equation in Hilbert’s Fourth Problem
Rafik Aramyan1,2
1Russian-Armenian (Slavonic) University, Yerevan, Armenia
2Institute of Mathematics, National Academy of Sciences, Yerevan, Armenia
Email: rafikaramyan@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 February 2014; revised 22 March 2014; accepted 1 April 2014
ABSTRACT
A solution of Hilbert’s fourth problem leads to the integral equation which can be called the generalized cosine equation. In the present paper, we propose an inversion formula for the solution of the generalized cosine equation using integral and stochastic geometry methods.
Keywords:Integral Geometry, Integral Equation, Finsler Metrics, Flag Density

1. Introduction
The integral-geometric approach to Hilbert’s fourth problem. The fourth problem in Hilbert’s famous collection of 1900, asks for the geometries, defined axiomatically, in which there exists a notion of length for which line segments are the shortest connections of their endpoints. The problem has later seen many transformation and interpretation. It was shown by G. Hamel that it is the same to ask (see [1] [2] ): Given an open convex subset 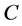 of
of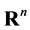 , determine all complete projective metrics on
, determine all complete projective metrics on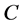 .
.
A metric 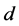 is called projective if it is continuous and linearly additive. Here
is called projective if it is continuous and linearly additive. Here 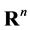 is the n-dimensional Euclidean space. There are two classical examples of projective metrics, already given by D. Hilbert. The first example is
is the n-dimensional Euclidean space. There are two classical examples of projective metrics, already given by D. Hilbert. The first example is 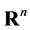 with the metric induced by a norm (a Minkowski space). Such metrics are the translation invariant projective metrics on
with the metric induced by a norm (a Minkowski space). Such metrics are the translation invariant projective metrics on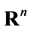 . The second example is what is now called a Hilbert geometry.
. The second example is what is now called a Hilbert geometry.
The modern approaches make it clear that the problem is at the basis of integral geometry, inverse problems and Finsler geometry (see [3] -[5] ). There is anintegral-geometric approach suggested by H.Busemann to construct class of projective metrics (see [3] ).
We denote by 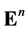 (
(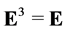 )—the space of hyperplanes in
)—the space of hyperplanes in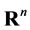 ,
,  -the unit sphere in
-the unit sphere in 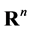 (the space of unit vectors),
(the space of unit vectors), 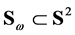 -the oriented great circle with pole at
-the oriented great circle with pole at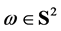 . By
. By 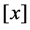 we denote the bundle of hyperplanes containing the point
we denote the bundle of hyperplanes containing the point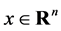 . Let
. Let 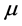 be a measure on
be a measure on 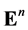 which satisfies
which satisfies
 (1)
(1)
and
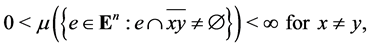 (2)
(2)
where 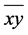 is the segment with endpoints
is the segment with endpoints 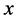 and
and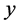 .
.
If we define
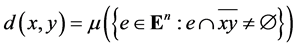 (3)
(3)
for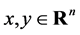 , then
, then 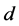 is a projective metric.
is a projective metric.
The question arises whether this construction produces all projective metrics on . First comes the A. V. Pogorelov-R. V. Ambartzumian-R. Aleksander result ([2] [6] [7] ) stating that in two dimensional case every projective metrics can be obtained by (3) with a measure in the space of lines in the plane. This essentially solves Hilbert’s fourth problem in two dimensional case (see also [8] ).
. First comes the A. V. Pogorelov-R. V. Ambartzumian-R. Aleksander result ([2] [6] [7] ) stating that in two dimensional case every projective metrics can be obtained by (3) with a measure in the space of lines in the plane. This essentially solves Hilbert’s fourth problem in two dimensional case (see also [8] ).
In dimension greater than two, the situation is different: not every projective metric on 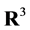 can be obtained by (3) with some measure
can be obtained by (3) with some measure 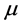 in
in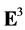 . This is already seen from the following construction.
. This is already seen from the following construction.
Now let  be a norm on
be a norm on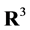 . Suppose that the projective metric
. Suppose that the projective metric  can be generated by (3) with translation invariant measure
can be generated by (3) with translation invariant measure  on
on . The translation invariant measure
. The translation invariant measure 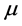 can be decomposed: there exists a finite even measure
can be decomposed: there exists a finite even measure 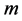 on
on 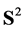 such that
such that 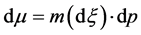 (see ([9] ), where
(see ([9] ), where  is the usual parametrization of a plane e: p is the distance of e from the origin o;
is the usual parametrization of a plane e: p is the distance of e from the origin o;  is the direction normal to e. We assume that
is the direction normal to e. We assume that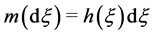 . Now the assumed representation (3), gives
. Now the assumed representation (3), gives
 (4)
(4)
The equation
 (5)
(5)
where  is a given even function while
is a given even function while 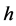 is the unknown function, is known as the zonoid equation. By a result of W. Blaschke the following is known (see ([10] ). If the even function
is the unknown function, is known as the zonoid equation. By a result of W. Blaschke the following is known (see ([10] ). If the even function 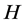 is sufficiently often differentiable then (5) has a uniquely determined continuous even solution not necessarily positive. If
is sufficiently often differentiable then (5) has a uniquely determined continuous even solution not necessarily positive. If 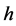 is the solution of (5), then we can define a translation invariant measure
is the solution of (5), then we can define a translation invariant measure  on
on  which satisfies (4).
which satisfies (4).
From now on, we restrict ourselves to Finsler metrics on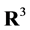 , since sufficiently smooth projective metrics are induced from Finsler metrics, and projective metrics can be approximated, uniformly on compact sets, by smooth projective Finsler metrics (see [2] [4] ).
, since sufficiently smooth projective metrics are induced from Finsler metrics, and projective metrics can be approximated, uniformly on compact sets, by smooth projective Finsler metrics (see [2] [4] ).
We define a Finsler metric on  as a continuous function
as a continuous function ![]() with the property that
with the property that 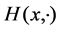 is a norm on
is a norm on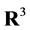 , for each
, for each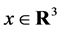 .
.
We consider locally finite signed measure 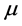 in the space
in the space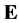 , which posses density with respect to the standard Euclidean motion invariant measure, i.e. (see [11] )
, which posses density with respect to the standard Euclidean motion invariant measure, i.e. (see [11] )
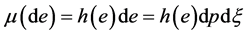 (6)
(6)
where 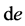 is an element of the standard measure. To define function
is an element of the standard measure. To define function 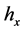 on
on 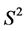 we consider the restriction of
we consider the restriction of  onto
onto  as a function on the hemisphere, since a direction completely determines a plane from
as a function on the hemisphere, since a direction completely determines a plane from . Then we extend the restriction to
. Then we extend the restriction to 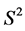 by symmetry. Thus
by symmetry. Thus

where 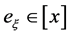 is the plane with normal
is the plane with normal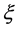 . Below
. Below 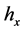 we call the restriction of
we call the restriction of 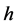 onto
onto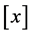 . In [2] , A. V. Pogorelov showed the following result.
. In [2] , A. V. Pogorelov showed the following result.
Theorem 1 If  is a smooth projective Finsler metric in
is a smooth projective Finsler metric in 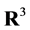 (
(![]() ), then there exists a uniquely determined locally finite signed measure
), then there exists a uniquely determined locally finite signed measure 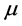 in the space
in the space , with continuous density function
, with continuous density function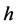 , such that, for
, such that, for 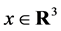
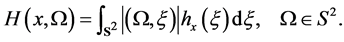 (7)
(7)
Here 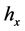 is the restriction of
is the restriction of 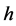 onto
onto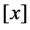 ,
, 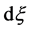 denotes the spherical Lebesgue measure on
denotes the spherical Lebesgue measure on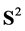 .
.
The measure  is also called a Crofton measure for the Finsler metric h (see [4] ). Different from the approach in [2] , Theorem 1 was proved by R.Schneider [12] using expansions in spherical harmonics.
is also called a Crofton measure for the Finsler metric h (see [4] ). Different from the approach in [2] , Theorem 1 was proved by R.Schneider [12] using expansions in spherical harmonics.
(7) defines a transform
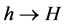
and we pose the problem of its inversion (i.e. reconstruction of h for given h). The Equation (7) where h is a given function and h is required, we call generalized cosine equation. We are interested in the solution of the generalized cosine equation defined by (7). Note that, the Equation (7) can have either no or exactly one continuous solution (see [10] ).
In case  is a translation invariant measure on
is a translation invariant measure on 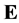 (
( ), (7) represents the zonoid Equation (5) playing an important role in convexity (see [10] ).
), (7) represents the zonoid Equation (5) playing an important role in convexity (see [10] ).
An inversion of the generalized cosine equation. The problem of finding the solution of (7) we reduce to find the solution of an other integral equation appearing in Combinatorial Integral Geometry. The concept of a flag density which was introduced and systematically employed by R. V. Ambartzumian, in [9] [11] will be of basic importance below.
We consider the so-called directed flags (below just a flag). A flag is a triad , where x is a point in
, where x is a point in 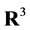 called the location of f, g is a directed line containing the point x, and e is an oriented plane (a plane with specified positive normal direction) containing g. There are two equivalent (and dual to each other) representations of a flag:
called the location of f, g is a directed line containing the point x, and e is an oriented plane (a plane with specified positive normal direction) containing g. There are two equivalent (and dual to each other) representations of a flag:
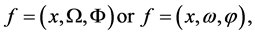
where 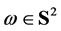 is the normal of e and
is the normal of e and  is the angular coordinate of the direction of g in
is the angular coordinate of the direction of g in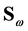 , while
, while  is the spatial direction of g and
is the spatial direction of g and 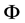 is the angular coordinate of the normal of e in
is the angular coordinate of the normal of e in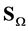 .
.
We use locally finite signed measure  in the space
in the space 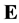 to define the following function (flag function) in the space of flags
to define the following function (flag function) in the space of flags 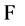 (so-called sine-square transform) (see [13] [14] )
(so-called sine-square transform) (see [13] [14] )
 (8)
(8)
Here  is the restriction of h onto
is the restriction of h onto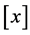 . To explain
. To explain  we write
we write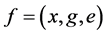 . Then
. Then 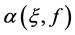 is the angle between g and the trace
is the angle between g and the trace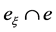 , where
, where 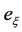 is the plane through the origin orthogonal to e. If we represent
is the plane through the origin orthogonal to e. If we represent 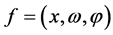 then
then
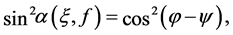 (9)
(9)
where 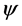 is the angular coordinate of the projection of
is the angular coordinate of the projection of 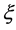 into the plane of the flag
into the plane of the flag . Note that (9) does not depend on the choice of the reference point on the plane of the flag
. Note that (9) does not depend on the choice of the reference point on the plane of the flag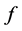 . The function
. The function 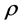 defined by (8) we call flag density of measure
defined by (8) we call flag density of measure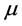 .
.
If the flag density 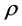 is sufficiently often differentiable, then (8) has a unique continuous solution
is sufficiently often differentiable, then (8) has a unique continuous solution 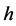 (see [9] [14] ). In [14] [15] (see also [16] -[18] in case
(see [9] [14] ). In [14] [15] (see also [16] -[18] in case 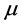 is a translation invariant measure) by author of the present paper using integral and stochastic geometry methods was found an inversion formula for (8) and reconstruct the density
is a translation invariant measure) by author of the present paper using integral and stochastic geometry methods was found an inversion formula for (8) and reconstruct the density  of signed measure
of signed measure  in terms of its smooth flag density
in terms of its smooth flag density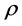 .
.
The problem of finding the solution of (7) we reduce to finding the flag density 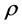 for which
for which
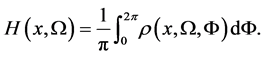 (10)
(10)
and using inversion formula of (8).
Now we describe the inversion formula of (7). We need to give the definitions of certain partial derivatives of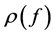 . With each directed flag we associate three orthogonal axes through x: by definition, axis
. With each directed flag we associate three orthogonal axes through x: by definition, axis 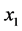 coincides with the direction of g; axis
coincides with the direction of g; axis 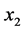 lies within e, is orthogonal to
lies within e, is orthogonal to 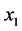 and is directed into the right half of e bounded by g; axis
and is directed into the right half of e bounded by g; axis 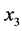 is coincides with the positive normal to
is coincides with the positive normal to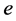 . We require that the axes
. We require that the axes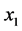 ,
, 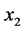 ,
,  form a left triad.
form a left triad.
By 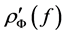 we denote the derivative of
we denote the derivative of 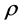 at f which corresponds to positive rotation of f around the axis g. By definition, the positive rotation of the space around the axis g appears clockwise, when we look in the direction of the axis g.
at f which corresponds to positive rotation of f around the axis g. By definition, the positive rotation of the space around the axis g appears clockwise, when we look in the direction of the axis g.
Also we denote by  the partial derivative in the argument x which is taken in the direction
the partial derivative in the argument x which is taken in the direction . In the special cases where
. In the special cases where 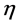 coincides with directions of the axes
coincides with directions of the axes 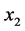 or
or 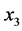 respectively, the values of
respectively, the values of 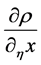
will be denoted as 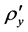 and
and 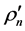 correspondingly.
correspondingly.
Our main result is the following. Let H be a sufficiently often differentiable function (![]() ). Also we assume that the Equation (7) has a solution. For every fixed
). Also we assume that the Equation (7) has a solution. For every fixed , we now solve the zonoid equation for the function
, we now solve the zonoid equation for the function . Since
. Since 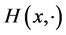 is smooth, there exists a smooth even solution
is smooth, there exists a smooth even solution 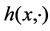 on
on . Then we put the function
. Then we put the function 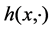 into Equation (8) instead of
into Equation (8) instead of 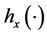 and found the flag function
and found the flag function 
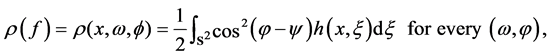 (11)
(11)
which depends on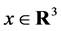 .
.
For a given plane e and a point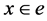 , the corresponding so-called bundle of flags we denote by
, the corresponding so-called bundle of flags we denote by
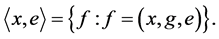
We consider so-called bundle mass of flag density 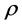 at
at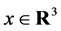 :
:
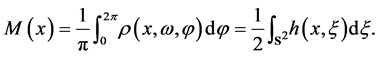 (12)
(12)
Note that the first integral in (12) does not depend on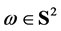 .
.
By 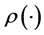 we denote the restriction of
we denote the restriction of  onto
onto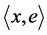 . The notation
. The notation  is reasonable since
is reasonable since  completely determines a flag from
completely determines a flag from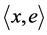 .
.
Theorem 2 Let H be a sufficiently often differentiable function (![]() ) and h defined on
) and h defined on 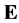 be the solution of (7). For a given plane
be the solution of (7). For a given plane 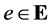 the following representation is valid
the following representation is valid
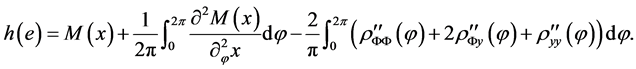 (13)
(13)
where x is a point on e, 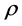 is defined by (11),
is defined by (11), 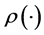 is the restriction of
is the restriction of 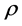 onto
onto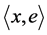 ,
, 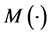 is the bundle mass function of
is the bundle mass function of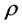 .
.
In Setion 3, we present the expression for 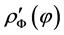 in terms of the derivatives of
in terms of the derivatives of 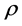 with respect to the parameters involved.
with respect to the parameters involved.
2. Convex Bodies and Measures in the Space of Planes
Equation (8) naturally emerges in Integral Geometry (see [13] [14] ). It proved in [14] that Equation (8) has the unique solution in the class of continuous functions and found an inversion formula. Here we present a short version of the proof of the formula for completeness.
Note that, in [16] the same problem was considered for the case 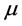 is a translation invariant measure on
is a translation invariant measure on 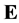 (
(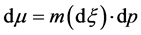 ). In [16] (see also [17] ) was obtained integral expression for the value of
). In [16] (see also [17] ) was obtained integral expression for the value of 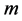 for a spherical domain bounded by a piecewise smooth curve and an inversion formula was found for a case
for a spherical domain bounded by a piecewise smooth curve and an inversion formula was found for a case 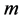 has a density, which first was found in [11] (see also [18] ).
has a density, which first was found in [11] (see also [18] ).
To invert Equation (8) we do the following. Let 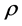 be a smooth function on the space of flags that is defined by (8) of a measure
be a smooth function on the space of flags that is defined by (8) of a measure 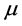 in
in 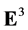 possessing continuous density h. We consider the restriction of h onto the set of planes tangent to a spherical domain. Then, by integral geometry methods we find the integral of the restriction over a spherical disc in terms of
possessing continuous density h. We consider the restriction of h onto the set of planes tangent to a spherical domain. Then, by integral geometry methods we find the integral of the restriction over a spherical disc in terms of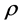 . Using this integrals we find an inversion formula for h.
. Using this integrals we find an inversion formula for h.
We need some results from integral geometry. Let 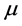 be a signed measure on
be a signed measure on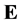 , possessing density h with respect to the invariant measure, i.e.
, possessing density h with respect to the invariant measure, i.e.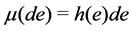 . Given a subset
. Given a subset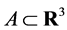 , by
, by 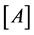 we denote the set of planes, that intersect a. Let
we denote the set of planes, that intersect a. Let  be a convex body with a sufficiently smooth boundary
be a convex body with a sufficiently smooth boundary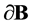 . By
. By  we denote the principal normal curvatures of
we denote the principal normal curvatures of  at a point
at a point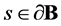 , and by
, and by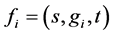 ,
, 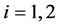 we denote the flag, where t is the plane tangent to
we denote the flag, where t is the plane tangent to 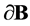 at the point
at the point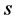 ,
,  is the directed line whose direction coincides with the i-th principal direction of curvature at
is the directed line whose direction coincides with the i-th principal direction of curvature at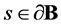 . In [14] (see also [19] ) the following representation has been obtained.
. In [14] (see also [19] ) the following representation has been obtained.
Theorem 3 Let 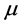 be a signed measure on
be a signed measure on , possessing density h with respect to the invariant measure. For any sufficiently smooth convex body
, possessing density h with respect to the invariant measure. For any sufficiently smooth convex body 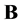 we have the following representation:
we have the following representation:
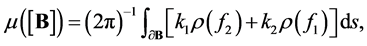 (14)
(14)
where 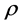 is the flag density of
is the flag density of 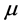 defined by (8),
defined by (8), 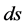 is an area element on
is an area element on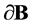 .
.
For the case 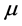 is a translation invariant measure on
is a translation invariant measure on  the representation first was found in [20] .
the representation first was found in [20] .
We will need some further definitions. By 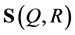 we denote the sphere with center
we denote the sphere with center 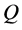 and radius
and radius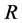 ,
, 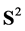 will stand for
will stand for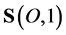 .
.
Assume h is the density of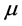 . We define the following function on
. We define the following function on 
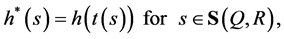
where 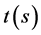 is the plane tangent to
is the plane tangent to 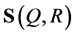 at
at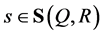 .
.
The measure![]() , where
, where 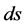 is an area element on
is an area element on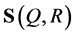 , we call the conditional measure on
, we call the conditional measure on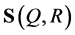 , generated by
, generated by 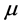 (or h).
(or h).
Let 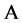 be a geodesically convex domain on
be a geodesically convex domain on , which is contained in some hemisphere. Let
, which is contained in some hemisphere. Let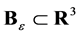 ,
, 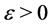 be the convex body bounded by
be the convex body bounded by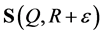 , planes tangent to
, planes tangent to 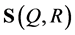 at points of
at points of 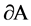 and the conical surface with the vertex Q and base A. In [14] , the following result was shown.
and the conical surface with the vertex Q and base A. In [14] , the following result was shown.
Theorem 4 Let  be a signed measure on
be a signed measure on 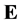 with continuous density h with respect to the invariant measure, and let
with continuous density h with respect to the invariant measure, and let 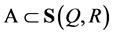 be an open convex domain contained in some hemisphere. Then
be an open convex domain contained in some hemisphere. Then
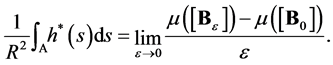 (15)
(15)
Using Theorems 3 and 4, one can calculate the values of the “conditional measure” for various domains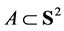 .
.
Now we calculate the conditional measure of a spherical disc 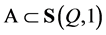 of spherical radius
of spherical radius  and using this result we find an inversion formula for (8). For translation invariant case the result was obtained in [16] (see also [17] ). Without loss of generality, one can consider Q as the origin O. On
and using this result we find an inversion formula for (8). For translation invariant case the result was obtained in [16] (see also [17] ). Without loss of generality, one can consider Q as the origin O. On  we consider usual spherical coordinates
we consider usual spherical coordinates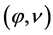 . The center of the disc chosen for the pole. We have:
. The center of the disc chosen for the pole. We have: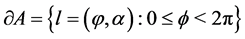 .
.
A flag f we call a tangent flag to A at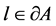 , if f is located at l, the plane of f is tangent to
, if f is located at l, the plane of f is tangent to 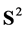 at
at 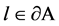
and the positive normal of the plane of f coincides with the outer normal to  at
at , the line of f is tangent to
, the line of f is tangent to 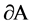 at l and the direction on the line of f corresponds to the motion along
at l and the direction on the line of f corresponds to the motion along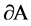 , which leaves (locally) A on the left hand side. By
, which leaves (locally) A on the left hand side. By 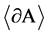 we denote the set of the tangent flags of A. The tangent flag at l is unique and therefore
we denote the set of the tangent flags of A. The tangent flag at l is unique and therefore 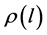 is a reasonable notation for the value of
is a reasonable notation for the value of 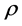 at the tangent flag located at l. By
at the tangent flag located at l. By 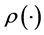 we denote the restriction of a flag function
we denote the restriction of a flag function 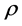 onto
onto .
.
Theorem 5 Let 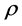 be a
be a  smooth flag function that is defined by (8) of a signed measure
smooth flag function that is defined by (8) of a signed measure 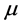 in
in 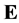 with continuous density h with respect to the invariant measure. Then for any spherical disc
with continuous density h with respect to the invariant measure. Then for any spherical disc 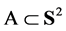
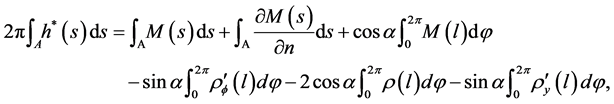 (16)
(16)
here n is the outer normal direction to 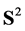 at s,
at s, 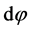 denotes the Lebesgue measure on
denotes the Lebesgue measure on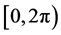 ,
, 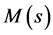 is the bundle mass of
is the bundle mass of  at s.
at s.
Proof of the Theorem 5. According to Theorem 4 we have to calculate 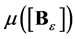 and
and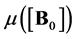 . In order to apply Theorem 3, instead of
. In order to apply Theorem 3, instead of 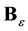 and
and 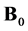 we consider their smooth versions
we consider their smooth versions 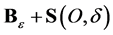 and
and  for some
for some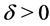 . We have
. We have
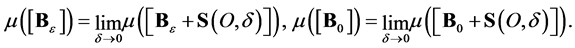 (17)
(17)
We divide the surfaces 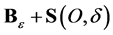 and
and 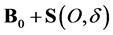 into domains (part of conical surface and part of spherical surface) and using (14) we get the expressions for
into domains (part of conical surface and part of spherical surface) and using (14) we get the expressions for 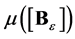 and
and  in terms of flag density. The last expressions we put into (15) and obtain (16). The realization of this procedure can be found in [14] [15] .
in terms of flag density. The last expressions we put into (15) and obtain (16). The realization of this procedure can be found in [14] [15] .
3. An Inversion Formula for (8)
To derive an inversion formula for (8), we express h in terms of given function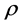 . Let
. Let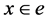 ,
, 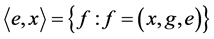 is the bundle of flags.
is the bundle of flags.
Theorem 6 Let 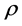 be a
be a  smooth function on the space of flags in
smooth function on the space of flags in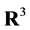 , that is defined by transform (8) of a signed measure
, that is defined by transform (8) of a signed measure 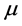 in
in 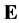 with continuous density h. For a given plane e the following representation is valid
with continuous density h. For a given plane e the following representation is valid
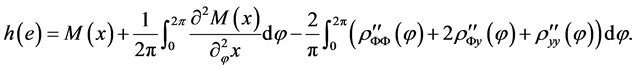 (18)
(18)
where x is a point on e, 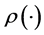 is the restriction of
is the restriction of 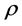 onto
onto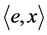 ,
, 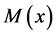 is the bundle mass of
is the bundle mass of  at x.
at x.
Proof of the Theorem 6. Let 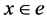 be a point. We consider a unit sphere
be a point. We consider a unit sphere 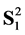 tangent to e at
tangent to e at 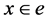 and denote by
and denote by 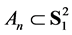 the spherical disk centered at x with the spherical radius
the spherical disk centered at x with the spherical radius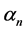 . By the mean-value theorem
. By the mean-value theorem
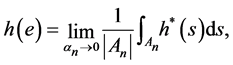 (19)
(19)
where ![]() is the area of
is the area of .
.
On , we consider usual spherical coordinates
, we consider usual spherical coordinates  with x chosen for the pole. We consider the restriction of the bundle mass
with x chosen for the pole. We consider the restriction of the bundle mass  onto
onto 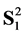 and by
and by 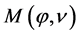 we denote the value of the restriction at
we denote the value of the restriction at![]() . Also, we consider the restriction of
. Also, we consider the restriction of 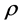 onto
onto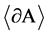 , where
, where 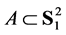 is the spherical disk centered at x with the spherical radius
is the spherical disk centered at x with the spherical radius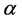 . By
. By 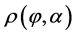 we denote the value of the restriction at
we denote the value of the restriction at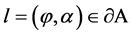 .
.
We represent the integral in (19) according to (16) and find the limit by decomposing the resulting terms in powers of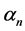 . We have
. We have
 (20)
(20)
To decompose other terms we need the following lemma.
Lemma 1 For any differentiable flag function 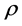
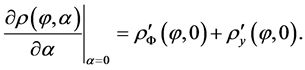 (21)
(21)
In its formulation, 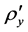 is defined assuming that the positive normal of e is parallel to the outer normal to
is defined assuming that the positive normal of e is parallel to the outer normal to 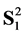 at x. Note, that
at x. Note, that 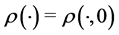 defined on the bundle of flags
defined on the bundle of flags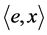 .
.
We have
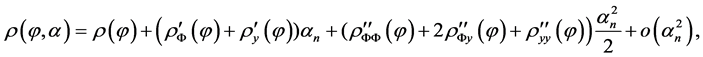 (22)
(22)
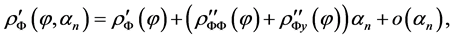 (23)
(23)
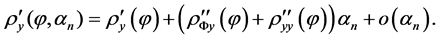 (24)
(24)
After proper substitution and taking into account that
![]() , we find
, we find
 (25)
(25)
Here 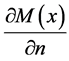 is the derivative of
is the derivative of 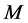 at
at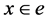 , in the direction of normal to
, in the direction of normal to 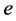 which is outer normal to
which is outer normal to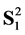 .
.
It is easy to prove that
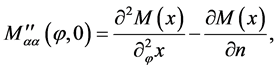 (26)
(26)
where 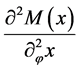 denotes the second derivative in the spatial direction which corresponds to the direction
denotes the second derivative in the spatial direction which corresponds to the direction 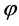
on e. After substitution (26) into (25) we obtain (18). Theorem 6 is proved.
The second integral in (13) contains the derivative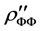 . To present the expression for
. To present the expression for 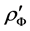 in terms of the derivatives of the function with respect to the parameters involved we introduce on
in terms of the derivatives of the function with respect to the parameters involved we introduce on 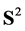 spherical coordinates in which
spherical coordinates in which 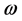 is specified by a pair
is specified by a pair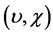 , where
, where 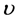 denotes the latitude of
denotes the latitude of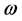 , and
, and 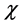 denotes its longitude. The corresponding derivatives with respect to
denotes its longitude. The corresponding derivatives with respect to  are given by the expressions (see. [17] ):
are given by the expressions (see. [17] ):
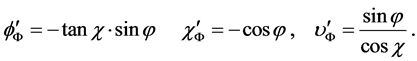 (27)
(27)
Using these formulas one can write the expression for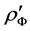 .
.
4. The Connection between Equations (7) and (8)
For a given line 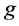 and a point
and a point , the corresponding bundle of flags we denote by
, the corresponding bundle of flags we denote by
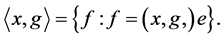
Now we integrate (8) over bundle of flags 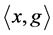 with respect to Lebesgue measure
with respect to Lebesgue measure 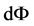 on
on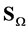 , where
, where 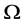 is the direction of
is the direction of 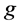 and
and 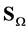 is the great circle on
is the great circle on 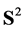 with pole at
with pole at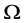 . We obtain
. We obtain
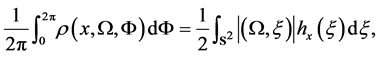 (28)
(28)
since from the definition of flag density we have (see [9] )
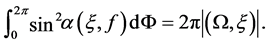 (29)
(29)
Note that one can obtain (29) using the cosine theorem of spherical geometry.
It follows from (28) if  is a smooth projective Finsler metric in
is a smooth projective Finsler metric in 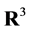 and
and 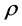 is a flag density such that
is a flag density such that
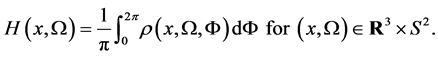 (30)
(30)
then Equations (7) and (8) have the same unique solution. Thus the problem of finding the solution of (7) we reduce to find flag density 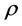 which satisfy (30) for a given smooth projective Finsler metric
which satisfy (30) for a given smooth projective Finsler metric .
.
Note that for a fixed 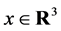 the restriction
the restriction 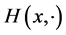 of a smooth projective Finsler metric
of a smooth projective Finsler metric 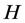 onto
onto 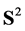 is uniquely determined by the restriction
is uniquely determined by the restriction 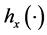 of the unique solution
of the unique solution 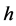 of (7) onto the bundle
of (7) onto the bundle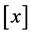 . The restriction
. The restriction  can be found by solution of the zonoid Equation (5) for
can be found by solution of the zonoid Equation (5) for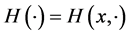 .
.
Also, note that for a fixed 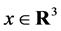 the restriction
the restriction 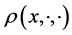 of the flag density
of the flag density 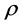 of the signed measure
of the signed measure 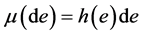 (where h is the unique solution of (7)) is uniquely determined by the restriction
(where h is the unique solution of (7)) is uniquely determined by the restriction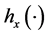 .
.
Hence for every fixed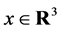 , we solve the zonoid equation for the function
, we solve the zonoid equation for the function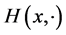 . Since
. Since 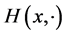 is a smooth function, there exists a smooth even solution
is a smooth function, there exists a smooth even solution 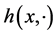 on
on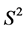 . Then we put the function
. Then we put the function 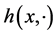 into Equation (8) instead of
into Equation (8) instead of 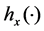 and find the flag density
and find the flag density 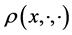 which depends on
which depends on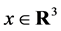 . Thus we find the flag density
. Thus we find the flag density  which satisfy (30). Substituting the flag density
which satisfy (30). Substituting the flag density 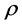 into (18) we get the solution of (8) which coincides with the solution of (7). Theorem 2 is proved.
into (18) we get the solution of (8) which coincides with the solution of (7). Theorem 2 is proved.
Fundings
This work was supported by State Committee Science MES RA, in frame of the research project SCS 13-1A244.
References
- Hamel, G. (1903) Uber die Geometrien in denen die Geraden die KUrzesten sind. Mathematische Annalen, 57, 231-264. http://dx.doi.org/10.1007/BF01444348
- Pogorelov, A.V. (1979) Hilbert’s Fourth Problem. Wilson and Sons, Hoboken (Russian Original: Izdat. “Nauka”, Moscow).
- Busemann, H. (1976) Problem IV: Desarguesian Spaces in Mathematical Developments Arising from Hilbert Problems. Proceedings of Symposia in Pure Mathematics, 28, 628 p.
- Schneider, R. (2006) Crofton Measures in Projective Finsler Spaces. In: Grinberg, E.L., Li, S., Zhang, G. and Zhou, J., Eds., Integral Geometry and Convexity, World Scientific, New Jersey, 67-98. http://dx.doi.org/10.1142/9789812774644_0006
- Schneider, R. (2002) On Integral Geometry in Projective Finsler Spaces. Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences), 37, 34-51.
- Ambartzumian, R.V. (1976) A Note on Pseudo-Metrics on the Plane. Zeitschrift fUr Wahrscheinlichkeitstheorie und Verwandte Gebiete, 37, 145-155. http://dx.doi.org/10.1007/BF00536777
- Alexander, R. (1978) Planes for Which the Lines Are the Shortest Paths between Points. Illinois Journal of Mathematics, 22, 177-190.
- Alvarez, P.J.C. (2003) Hilberts Fourth Problem in Two Dimensions I. In: Katok, S., Sossinsky, A. and Tabachnikov, S., Eds., Mass Selecta: Teaching and Learning Advanced Undergraduate Mathematics, American Mathematical Society, Providence, 165-183.
- Ambartzumian, R.V. (1990) Factorization Calculus and Geometric Probability. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139086561
- Schneider, R. and Weil, W. (1983) Zonoids and Related Topics. Convexity and Its Applications. In: Gruber, P.M. and Wills, J.M., Eds., Convexity and Its Applications, Birkhauser, Basel, 296-317.
- Ambartzumian, R.V. (1987) Combinatorial Integral Geometry, Metric and Zonoids. Acta Applicandae Mathematicae, 9, 3-27. http://dx.doi.org/10.1007/BF00580819
- Schneider, R. (1967) Zu einem Problem von Shephard Uber die Projektionen konvexer Korper. Mathematische Zeitschrift, 191, 71-82. http://dx.doi.org/10.1007/BF01135693
- Ambartzumian, R.V. and Oganyan V.K. (1994) Finite Additive Functionals in the Space of Planes, I. Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences), 29, 3-51.
- Aramyan, R.H. (1994) Measure Generation in the Space of Planes and Spherical Euler Functionals. Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences), 29, 52-74.
- Aramyan, R.H. (2011) Reconstruction of Measures in the Space of Planes. Lobachevskii Journal of Mathematics, 32, 241-246. http://dx.doi.org/10.1134/S1995080211040044
- Aramyan, R.H. (1992) Recovering Rose of Directions from Flag Densities in R3. Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences), 27, 22-35.
- Aramyan, R.H. (2009) Solution of One Integral Equation on the Sphere by Methods of Integral Geometry. Doklady Mathematics, 79, 325-328. http://dx.doi.org/10.1134/S1064562409030077
- Panina, G.Y. (1994) Flag densities in R3. Journal of Contemporary Mathematical Analysis (Armenian Academy of Sciences), 29, 76-80.
- Aramyan, R.H. (2010) Measure of Planes Intersecting a Convex Body. Sutra: International Journal of Mathematical Science Education, 3, 1-7.
- Panina, G.Y. (1987) Convex Bodies and Translation Invariant Measures in R3. Izvestiya Akademii Nauk Armyanskoi SSR. Matematika, 24, 478-489.

