Advances in Pure Mathematics
Vol.4 No.3(2014), Article ID:44342,6 pages DOI:10.4236/apm.2014.43012
On the Full Transitivity of a Cotorsion Hull of the Pierce Group
Tariel Kemoklidze
Department of Mathematics, Akaki Tsereteli State University, Kutaisi, Georgia
Email: kemoklidze@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 13 February 2014; revised 13 March 2014; accepted 18 March 2014
ABSTRACT
The paper considers the problem of full transitivity of a cotorsion hull 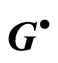 of a separable primary group
of a separable primary group 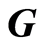 when a ring of endomorphisms
when a ring of endomorphisms  of the group
of the group  has the form
has the form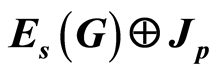 , where
, where 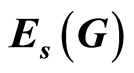 is a subring of small endomorphisms of the ring
is a subring of small endomorphisms of the ring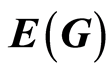 , whereas
, whereas 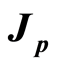 is a ring of integer
is a ring of integer  -adic numbers. Investigation of the issue of full transitivity of a group is essentially helpful in studying its fully invariant subgroups as well as the lattice formed by these subgroups. It is proved that in the considered case, the cotorsion hull is not fully transitive. A lemma is proposed, which can be used in the study of full transitivity of a group and in other cases.
-adic numbers. Investigation of the issue of full transitivity of a group is essentially helpful in studying its fully invariant subgroups as well as the lattice formed by these subgroups. It is proved that in the considered case, the cotorsion hull is not fully transitive. A lemma is proposed, which can be used in the study of full transitivity of a group and in other cases.
Keywords:Full Transitivity of a Group; Cotorsion Hull; Fully Invariant Subgroup

1. Introduction
The groups discussed in the paper are abelian and the operation is written in additive terms. We use here the notation and terminology of the monographs [1] [2] .
The symbol 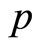 denotes a fixed prime number.
denotes a fixed prime number. 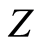 and
and 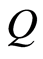 are respectively the groups of integer and rational numbers. A subgroup
are respectively the groups of integer and rational numbers. A subgroup 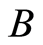 of the group
of the group 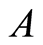 is called fully invariant if it is self-mapped for any endomorphism of the group
is called fully invariant if it is self-mapped for any endomorphism of the group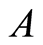 .
.
The knowledge of the construction of fully invariant subgroups of an abelian group and their lattice is essentially helpful in the study of the properties of the group itself and also in the investigation of the properties of its rings of endomorphisms and quasi-endomorphisms, the group of automorphisms and other algebraic systems connected with the initial group.
For a sufficiently wide class of  -groups these topics were studied by R. Baer, I. Kaplansky, P. Linton, R. Pierce, D. Moore, E. Hewett and others. The works of A. Mader, R. Göbel, P. A. Krylov, S. Ya. Grinshpon, A. I. Moskalenko and other authors are dedicated to the investigation of these topics in torsion-free and mixed groups.
-groups these topics were studied by R. Baer, I. Kaplansky, P. Linton, R. Pierce, D. Moore, E. Hewett and others. The works of A. Mader, R. Göbel, P. A. Krylov, S. Ya. Grinshpon, A. I. Moskalenko and other authors are dedicated to the investigation of these topics in torsion-free and mixed groups.
However little is known about the results obtained in this area for the class of cotorsion groups. A group 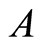 is called a cotorsion group if its extension by means of any torsion-free group
is called a cotorsion group if its extension by means of any torsion-free group  splits as follows:
splits as follows:
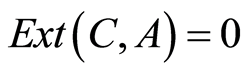 . The importance of the class of cotorsion groups in the theory of abelian groups is due to two factors: for any groups
. The importance of the class of cotorsion groups in the theory of abelian groups is due to two factors: for any groups ,
,  , the group
, the group 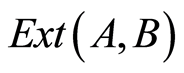 is a cotorsion one and any reduced group
is a cotorsion one and any reduced group  is isomorphically embeddable in the group
is isomorphically embeddable in the group  called the cotorsion hull of the group
called the cotorsion hull of the group . If the torsion part of the group
. If the torsion part of the group 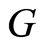 is denoted by
is denoted by , then
, then

where . Thus the study of cotorsion groups essentially reduces to the study of groups of the form
. Thus the study of cotorsion groups essentially reduces to the study of groups of the form , where
, where 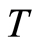 is a
is a  -primary group.
-primary group.
It is noteworthy that endomorpohisms in cotorsion groups are completely defined by their action on the torsion part and, as shown by W. May and E. Toubassi [3] , for a mixed group 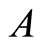 the ring of endomorphisms
the ring of endomorphisms 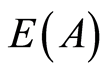 is isomorphic to
is isomorphic to 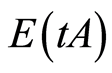 if and only if
if and only if 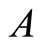 is a fully invariant subgroup of the cotorsion hull
is a fully invariant subgroup of the cotorsion hull .
.
The notion of full transitivity of a group plays an essential role in describing the lattice of fully invariant subgroups.
By the  -indicator of an element
-indicator of an element  of the group
of the group  we mean an increasing sequence of ordinal numbers
we mean an increasing sequence of ordinal numbers

where 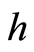 is the generalized
is the generalized 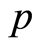 -height of an element, i.e. for
-height of an element, i.e. for 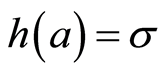 if
if 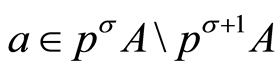 and
and . Now for the set of indicators we can introduce the order
. Now for the set of indicators we can introduce the order
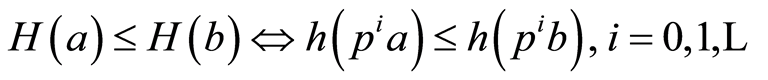
A reduced  -group is called fully transitive if for arbitrary elements
-group is called fully transitive if for arbitrary elements  and
and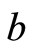 , when
, when  there exists an endomorphism
there exists an endomorphism  of the group such that
of the group such that . The class of fully transitive groups includes such important groups as separable
. The class of fully transitive groups includes such important groups as separable 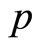 -groups, algebraically compact groups and quasi-pure injective groups.
-groups, algebraically compact groups and quasi-pure injective groups.
Using the indicators of fully transitive groups we can describe the lattice of fully invariant subgroups (see [4] -[11] ).
For a module over a commutative ring, A. Mader formulated a general scheme that can be used to describe the lattice of fully invariant submodules of the module (see [10] , Theorem 2.1 or [12] , Theorem 1.1).
In the same way as we did for a 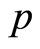 -group we define the notion of full transitivity for the group
-group we define the notion of full transitivity for the group
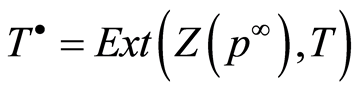 . According to A. Mader [10] , an algebraically compact group is fully transitive and described with the aid of indicators the lattice of fully invariant subgroups of this group. This means to describe the lattice of fully invariant subgroups of the group
. According to A. Mader [10] , an algebraically compact group is fully transitive and described with the aid of indicators the lattice of fully invariant subgroups of this group. This means to describe the lattice of fully invariant subgroups of the group  when
when 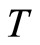 is a torsion-complete group. When
is a torsion-complete group. When  is the direct sum of cyclic
is the direct sum of cyclic 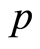 -groups, A. Moskalenko [11] proved that
-groups, A. Moskalenko [11] proved that  is also fully transitive and described by means of indicators the lattice of fully invariant subgroups of the group
is also fully transitive and described by means of indicators the lattice of fully invariant subgroups of the group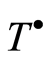 . In general, for the separable primary group
. In general, for the separable primary group , the cotorsion hull
, the cotorsion hull  is not fully transitive. In particular if
is not fully transitive. In particular if 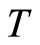 is an infinite direct sum of torsion-complete groups, then, as shown by the author [13] , the group
is an infinite direct sum of torsion-complete groups, then, as shown by the author [13] , the group 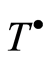 is not fully transitive and in that case the lattice of fully invariant subgroups of the group
is not fully transitive and in that case the lattice of fully invariant subgroups of the group  cannot be described by means of indicators (see [12] ).
cannot be described by means of indicators (see [12] ).
R. Pierce [14] considered the primary group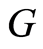 , a ring of whose endomorphisms has the form
, a ring of whose endomorphisms has the form
 (1.1)
(1.1)
where 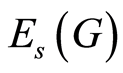 is the ring of small endomorphisms of the group
is the ring of small endomorphisms of the group 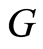 which is the ideal of the ring of endomorphisms
which is the ideal of the ring of endomorphisms  of the group
of the group , whereas
, whereas 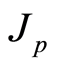 is the ring of integer
is the ring of integer  -adic numbers. A small endomorphism of the group
-adic numbers. A small endomorphism of the group 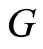 is defined as follows (see [14] ).
is defined as follows (see [14] ).
For all  there exists an integer
there exists an integer  such that
such that
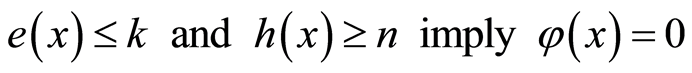 . (1.2)
. (1.2)
The Pierce group  is important when studying the ring of endomorphisms of abelian groups (see [15] ). The aim of the present paper consists in elucidating the full transitivity of the cotorsion hull
is important when studying the ring of endomorphisms of abelian groups (see [15] ). The aim of the present paper consists in elucidating the full transitivity of the cotorsion hull  and also in finding the conditions, under which the cotorsion hull is not fully transitive.
and also in finding the conditions, under which the cotorsion hull is not fully transitive.
2. Full Transitivity of the Cotorsion Hull of the Pierce Group
As mentioned above, R. Pierce [14] considered the separable primary group 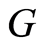 with a standard basic subgroup
with a standard basic subgroup
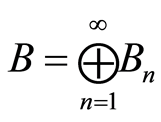 ,
,  ,
, 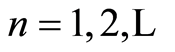 ,
, 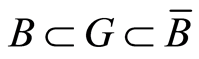 , where
, where 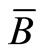 is a torsion-complete group, i.e. the torsion part of a
is a torsion-complete group, i.e. the torsion part of a 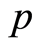 -adic completion of the group
-adic completion of the group . The cardinality is
. The cardinality is 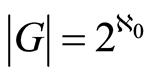 and the ring of endomorphisms of the group
and the ring of endomorphisms of the group  has form (1.1).
has form (1.1).
To study the full transitivity of the group , we use the following representation of elements of the cotorsion hull of
, we use the following representation of elements of the cotorsion hull of 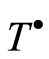 given by A. Moskalenko [11] for the separable
given by A. Moskalenko [11] for the separable  -group
-group 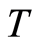
 . (2.1)
. (2.1)
Representation of elements in this form makes it easy to calculate the height and the indicator. In particular, if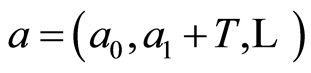 , then
, then
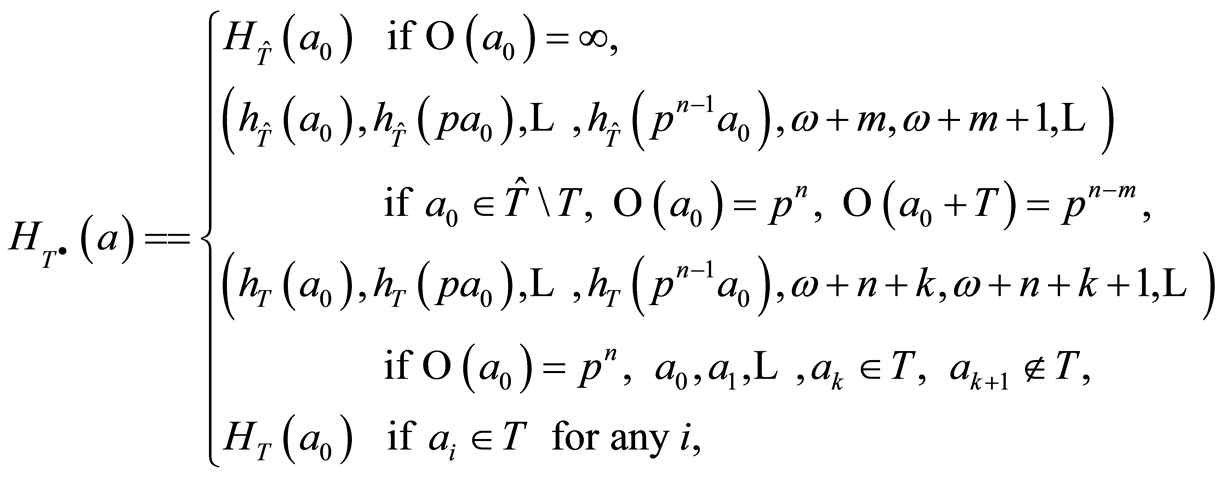 (2.2)
(2.2)
where  is the smallest infinite ordinal number.
is the smallest infinite ordinal number.
Let  be a basic subgroup of the reduced separable
be a basic subgroup of the reduced separable 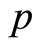 -group
-group 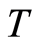 lying between
lying between 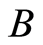 and
and . Elements
. Elements ,
, 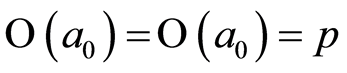 ,
,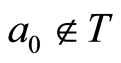 . As is know, an endomorphism
. As is know, an endomorphism  of the group
of the group  extends uniquely to an endomorphism of
extends uniquely to an endomorphism of .
.
The following lemma is true.
Lemma 2.1. If 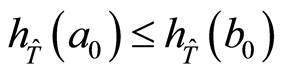 and there exists no endomorphism
and there exists no endomorphism  of the group
of the group 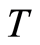 for which
for which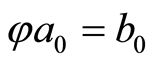 , then a cotorsion hull
, then a cotorsion hull 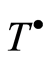 is not fully transitive.
is not fully transitive.
Proof. Consider two elements
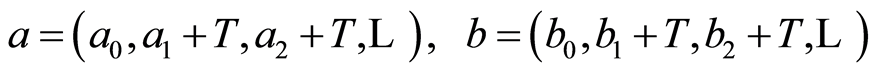
of the group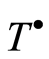 . Then by the condition of the theorem and (2.2) we have
. Then by the condition of the theorem and (2.2) we have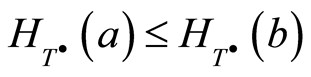 . As is known, each endomorphism of the group
. As is known, each endomorphism of the group  extends uniquely to an endomorphism of the group
extends uniquely to an endomorphism of the group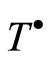 . We will show that if for an endomorphism
. We will show that if for an endomorphism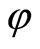 ,
,  , then
, then . Let
. Let
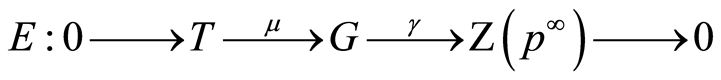 (2.3)
(2.3)
be the element of the group  defined by the sequence
defined by the sequence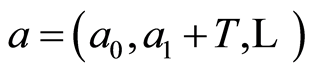 . For an endomorphism
. For an endomorphism  of the group
of the group  let us show that
let us show that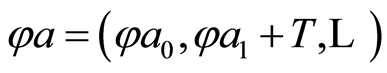 . According to ([1] , Section 50), the extension of
. According to ([1] , Section 50), the extension of 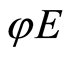 is defined from the commutative diagram
is defined from the commutative diagram
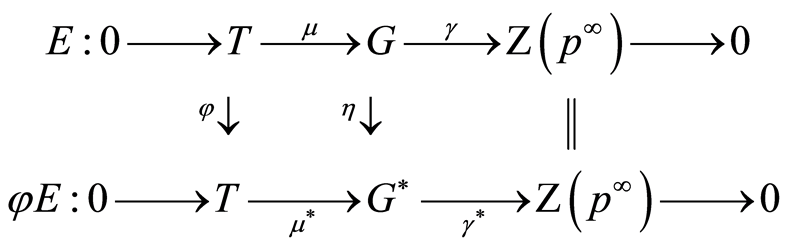 (2.4)
(2.4)
where  is the identical inclusion,
is the identical inclusion,
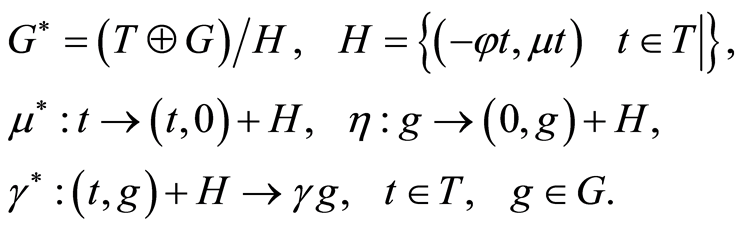
The commutativity of diagram (2.4) immediately follows from the definition of these homomorphisms.
To extension (2.3) there corresponds the sequence , where elements are defined as follows: fix a system of generators
, where elements are defined as follows: fix a system of generators 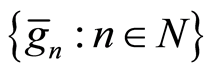 of the group
of the group ,
, 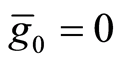 ,
,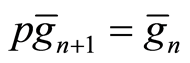 . Let
. Let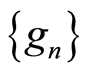 ,
, 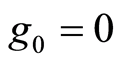 , be a system of representatives of the adjacent classes
, be a system of representatives of the adjacent classes 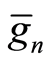 of the group
of the group ,
, 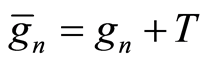 ,
, 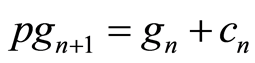 ,
,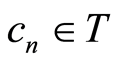 . Denote
. Denote
 .
.
Then for each ,
,
 .
.
For an endomorphism 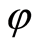 of the group
of the group 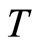 we have
we have ,
,  , and can define
, and can define
 (2.5)
(2.5)
It is obvious that the right-hand part of equality (2.5) defines the extension of an endomorphism  on
on  and if
and if  is some other endomorphism of the group
is some other endomorphism of the group , which induces
, which induces 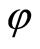 on
on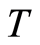 , then
, then  contains
contains  and
and 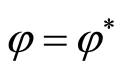 ([1] , Proposition 34.1). From (2.5) we have
([1] , Proposition 34.1). From (2.5) we have
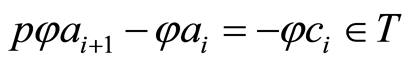 .
.
Now we can consider an element
 (2.6)
(2.6)
of the group  and with its aid define the corresponding short exact sequence.
and with its aid define the corresponding short exact sequence.
Let  be the group defined by a system of generators
be the group defined by a system of generators 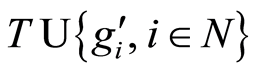 which are defined by the relations of the group
which are defined by the relations of the group 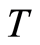 and the equalities
and the equalities ,
, 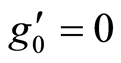 ,
,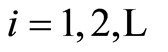 . Then
. Then
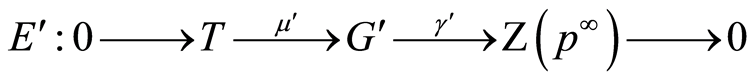 (2.7)
(2.7)
where 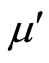 is the identical inclusion and, for each element
is the identical inclusion and, for each element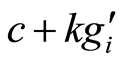 ,
, 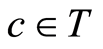 ,
,  ,
,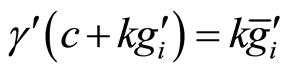 is a short exact sequence. To extension (2.7) there corresponds sequence (2.6) (see [11] , Proof of Theorem 1). Let us show that by using extensions (2.3) and (2.7) we can compose the commutative diagram
is a short exact sequence. To extension (2.7) there corresponds sequence (2.6) (see [11] , Proof of Theorem 1). Let us show that by using extensions (2.3) and (2.7) we can compose the commutative diagram
 (2.8)
(2.8)
where 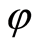 is the above-mentioned endomorphism and
is the above-mentioned endomorphism and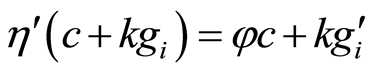 ,
,  ,
,  ,
,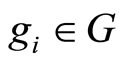 . Indeed, from the definition of a triple
. Indeed, from the definition of a triple 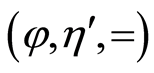 we immediately conclude that (2.8) is a commutative diagram.
we immediately conclude that (2.8) is a commutative diagram.
Thus we have shown that (2.4) and (2.8) are commutative diagrams. Then, according to ([1] , Section 50),  and
and 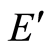 are equivalent extensions and thereby define one and the same sequence from
are equivalent extensions and thereby define one and the same sequence from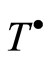 . But, by virtue of our construction,
. But, by virtue of our construction, 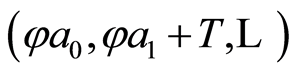 is the sequence corresponding to the extension
is the sequence corresponding to the extension ; therefore it corresponds to the extension
; therefore it corresponds to the extension , too. Thus
, too. Thus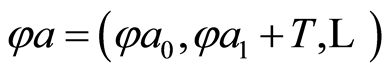 . Therefore if the endomorphism
. Therefore if the endomorphism  maps the element
maps the element 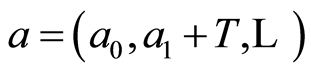 into
into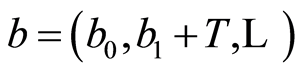 , then
, then , i.e. we have proved more than what has been mentioned at the beginning of the proof of the lemma. Thus it obviously follows that if there exists no endomorphism
, i.e. we have proved more than what has been mentioned at the beginning of the proof of the lemma. Thus it obviously follows that if there exists no endomorphism  of the group
of the group  for which
for which , then there exists no endomorphism
, then there exists no endomorphism 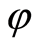 of the group
of the group 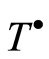 which maps the element
which maps the element 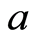 into
into , i.e.
, i.e. 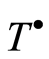 is not fully transitive. The lemma is proved.
is not fully transitive. The lemma is proved.
For the Pierce group 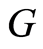 the following statement is true.
the following statement is true.
Theorem 2.1. The cotorsion hull  of the group
of the group 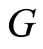 is not fully transitive.
is not fully transitive.
Proof. We use representation (2.1) of cotorsion hull elements and assume that  and
and  are elements of the group
are elements of the group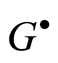 , where
, where ,
,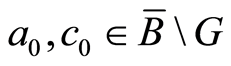 . By virtue of (11, Item 2), elements
. By virtue of (11, Item 2), elements 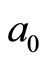 and
and 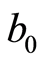 can be written in the form
can be written in the form
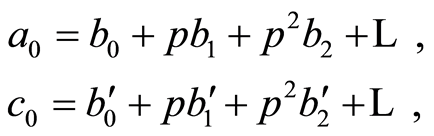
where ,
, . Since
. Since 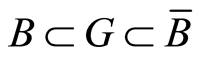 and
and  is infinite, taking into account ([14] : Lemma 15.1, Theorem 15.4) we can assume that
is infinite, taking into account ([14] : Lemma 15.1, Theorem 15.4) we can assume that
 (2.9)
(2.9)
By (2.2) we have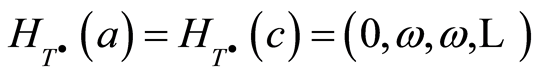 , i.e. the following condition is fulfilled
, i.e. the following condition is fulfilled
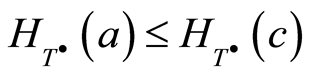 .
.
Let  be an endomorphism of the group
be an endomorphism of the group . Using (1.1) we have
. Using (1.1) we have , where
, where  is a small endomorphism of the group
is a small endomorphism of the group  and
and  is the
is the  -adic number
-adic number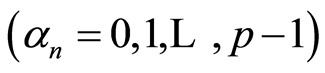
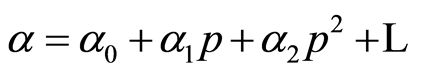 . As is known ([1] , Section 39), the endomorphism
. As is known ([1] , Section 39), the endomorphism  uniquely extends to the endomorphism
uniquely extends to the endomorphism 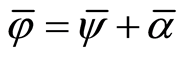 of the group
of the group 
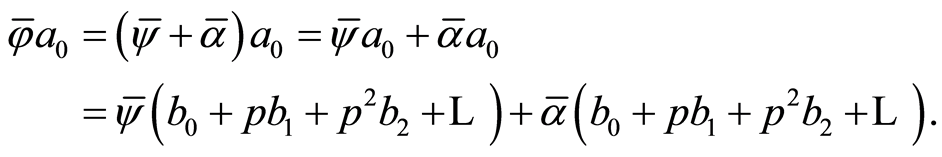
Since
 (2.10)
(2.10)
and 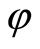 is a small endomorphism of the group
is a small endomorphism of the group 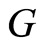 (see (1.2)), starting with some
(see (1.2)), starting with some 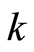 we have
we have
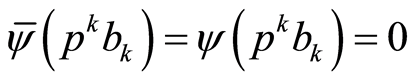 .
.
Therefore
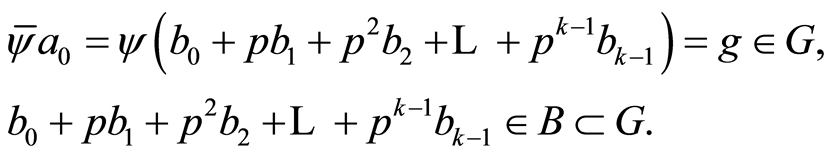
On the other hand, from (2.10) we obtain
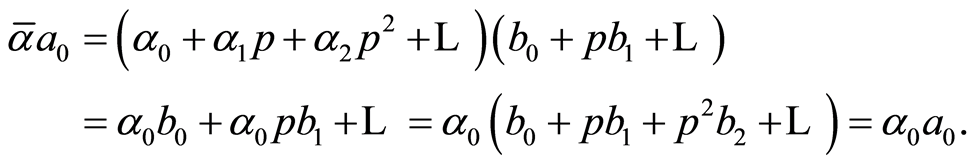
Therefore
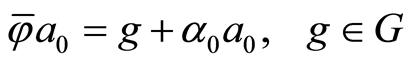
But  since
since ,
, 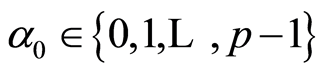 , and in that case the equality
, and in that case the equality  would contradict condition (2.9). Therefore
would contradict condition (2.9). Therefore
 .
.
Thus there exists no endomorphism  of the group
of the group 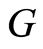 which extends to the endomorphism
which extends to the endomorphism 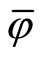 of the group
of the group 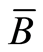 and
and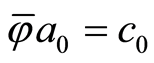 . Then from Lemma 1.1 it follows that Theorem 2.1 is valid.
. Then from Lemma 1.1 it follows that Theorem 2.1 is valid.
Note that one more example of a separable primary group, the cotorsion hull of which is not fully transitive, can be found in ([11] , item 3).
As mentioned above, if the separable primary group 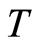 is a direct sum of cyclic
is a direct sum of cyclic 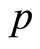 -groups or a cotorsioncomplete group, then the cotorsion hull
-groups or a cotorsioncomplete group, then the cotorsion hull  is fully transitive. In 1993, at Professor A. Fomin’s seminar A. Moskalenko made a conjecture that
is fully transitive. In 1993, at Professor A. Fomin’s seminar A. Moskalenko made a conjecture that  is fully transitive only in these two cases. The proved lemma and theorem may serve as a positive argument in favor of this conjecture.
is fully transitive only in these two cases. The proved lemma and theorem may serve as a positive argument in favor of this conjecture.
Acknowledgements
This study was supported by the grant (ATSU-2013/44) of Akaki Tsereteli University.
References
- Fuchs, L. (1970) Infinite Abelian Groups. I. Pure and Applied Mathematics, Vol. 36, Academic Press, New York.
- Fuchs, L. (1973) Infinite Abelian Groups. II. Pure and Applied Mathematics, Vol. 36-II, Academic Press, New York.
- May, W. and Toubassi, E. (1976) Endomorphisms of Abelian Groups and the Theorem of Baer and Kaplansky. Journal of Algebra, 43, 1-13. http://dx.doi.org/10.1016/0021-8693(76)90139-3
- Baer, R. (1935) Type of Elements and Characteristic Subgroups of Abelian Groups. Proceedings of the London Mathematical Society, Series 2, 39, 481-514. http://dx.doi.org/10.1112/plms/s2-39.1.481
- Kaplansky, I. (1969) Infinite Abelian Groups. The University of Michigan Press, Ann Arbor.
- Linton, R.S. (1976) On Fully Invariant Subgroups of Primary Abelian Groups. Michigan Mathematical Journal, 22, 281-284. http://dx.doi.org/10.1307/mmj/1029001528
- Moore, J.D. and Hewett, E.J. (1971/72) On Fully Invariant Subgroups of Abelian p-Groups. Commentarii Mathematici Universitatis Sancti Pauli, 20, 97-106.
- Göbel, R. (1974) The Characteristic Subgroups of the Baer-Specker Group. Mathematische Zeitschrift, 140, 289-292. http://dx.doi.org/10.1007/BF01214169
- Grinshpon, S.Ya. and Krylov, P.A. (2005) Fully Invariant Subgroups, Full Transitivity, and Homomorphism Groups of Abelian Groups. Journal of Mathematical Sciences, 128, 2894-2997. http://dx.doi.org/10.1007/s10958-005-0245-5
- Mader, A. (1970) The Fully Invariant Subgroups of Reduced Algebraically Compact Groups. Publicationes Mathematicae Debrecen, 17, 299-306.
- Moskalenko, A.I. (1989) Cotorsion Hull of a Separable Group. Algebra i Logika, 28, 207-226. http://dx.doi.org/10.1007/BF01979377
- Kemoklidze, T. (2013) The Lattice of Fully Invariant Subgroups of the Cotorsion Hull. Advances in Pure Mathematics, 3, 670-697. http://www.emis.de/journals/GMJ/vol13/contents.htm http://dx.doi.org/10.4236/apm.2013.38090
- Kemoklidze, T. (2006) On the Full Transitivity of a Cotorsion Hull. Georgian Mathematical Journal, 13, 79-84.
- Pierce, R.S. (1963) Homomorphisms of Primary Abelian Groups. In: Topics in Abelian Groups, Scott, Foresman and Co., Chicago, 215-310.
- Stringall, R.W. (1967) Endomorphism Rings of Primary Abelian Groups. Pacific Journal of Mathematics, 20, 535-557. http://dx.doi.org/10.2140/pjm.1967.20.535

