ABSTRACT

We discuss two types of maps on operator spaces. Firstly, through example we show that there is an isometry on unit sphere of an operator space cannot be extended to be a complete isometry on the whole operator space. Secondly, we give a new characterization for complete isometry by the concept of approximate isometry.

Keywords:Unit Sphere, Approximate Isometry, Complete Isometry

1. Introduction

The theory of operator spaces is very recent. It was developed after Ruan’s thesis (1988) by Effros and Ruan and Blecher and Paulsen and Pisier.

Theorem (Ruan) in [1] suppose that 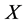is a vector space, and that for each 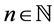we are given a norm 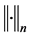on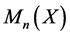. Then 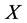is completely isometrically linearly isomorphic to a subspace of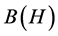, for some Hilbert space, if and only if conditions (R1) and (R2) above hold.

R1:R2:.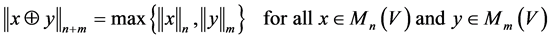

In this new category, the objects remain Banach spaces but the morphisms become the completely bounded maps. In fact, the completely bounded maps appeared in the early 1980s following Stinespring’s pioneering work (1955) and Arveson’s fundamental results (1969) on completely positive maps see [1] -[4] .

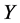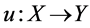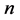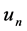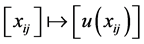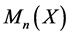Definition 1 Let and be operator spaces and that be a linear map. For a positive integer, we write for the associated map from to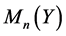. This is often called the (nth) amplification of, and may also be thought of as the map 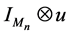on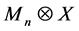. A map 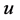is completely bounded (in short c.b.) if

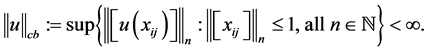
We denote by 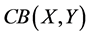the Banach space of all c.b. maps from 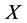into 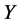equipped with the c.b. norm. If 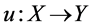is c.b. map, we have

and

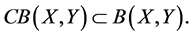
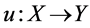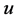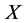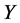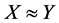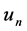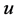The notion of isomorphism is replaced by that of “complete isomorphism”. If is a completely bounded linear bijection, and if its inverse is completely bounded too, then we say that is complete isomorphism. In this case, we say that and are completely isomorphic and we write “as operator spaces”. Similarly, if is an isometry for any, then we say that is complete isometry. We often identify two operator spaces 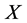and if they are completely isometrically isomorphic. In this case we often write “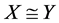as operator spaces”.

In 1932 [5] , Mazur and Ulam got the famous theorem that a surjective isometry between two real normed spaces must be linear up to translation, which started the study of the theory of isometry. Many researchers have tried to generalize it. In 1972 Mankiewicz [6] considered the extension problem for isometries and every surjective isometry between the open connected subsets of two normed spaces can be extended to a surjective affine isometry on the whole space. This result can be seen as local Mazur-Ulam Theorem. From this result, we get easily that a map’s property on unit ball of a normed space determines the relationship between distance preserving and linearity. In 1987, D.Tingley raised the following problem (the isometric extension problem) in [7] :

Problem. Suppose that 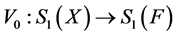is a surjective isometric mapping, does there exist a linear isometric mapping 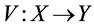such that?

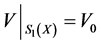D. Tingley, who is the first one to study the problem, gave some results in [7] under the condition that 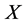and 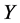are finite dimensional spaces. More precisely, the answer can be formulated as follows: Suppose that 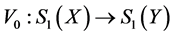is a surjective isometric mapping, then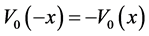, i.e. is an odd mapping. In the complex spaces, the answer to Tingleys problem is negative. For example, we take (complex plane) and. Some affirmative results have been obtained between classical real Banach spaces, which had been shown in [8] -[12] . The recent development on this problem you can find in [13] . We ask can we discuss the isometric extension problem in operator space category? Through example, we give some results on it.

2. Some Examples about Isometric Extension Problem on Operator Spaces

Theorem Let 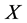be 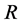(resp.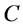, , 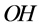, , 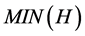, 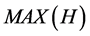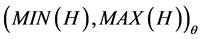etc.). Let 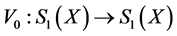be a 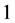-Lip operator. Then 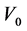can be extended to a linearly complete isometry on.

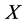Proof. By [11] , 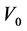can be linearly extended to the whole Hilbert space. Since 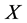are homogeneous operator space, the the result can be got directly.

How about the result on non-homogeneous operator spaces?

Theorem There exists an isometry 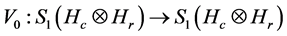such that there is no complete isometry 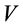on the whole space 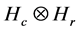satisfying.

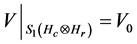Proof. Let 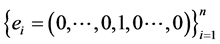be the basis of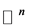. To express conveniently, we denote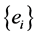 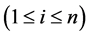to be the basis of the n-dimensional column Hilbert operator space 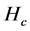and 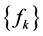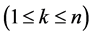be the basis of the n-dimensional row Hilbert operator space. Then 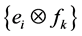constructs a basis of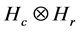. Give the 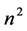elements an order defined as

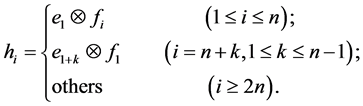
Let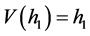, 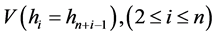and 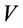maps other elements 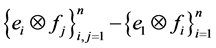of the basis t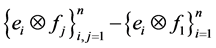o. So 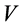forms a permutation among the basis of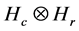. By the isometric theory on Hilbert space, 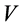is an isometry on the Banach space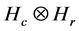. Of course let 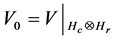is an isometry between unit sphere of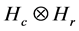. But 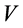is not complete isometry on.

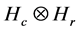Indeed, for 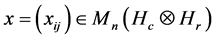where

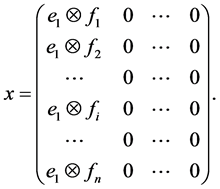
Then

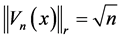It is easy to calculate that but. So 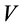is not complete isometry.

3. On Stability of (-Isometries of Operator Spaces

The study on the stability of ò-isometry is from Banach Space Theory.

Let 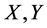be two Banach spaces and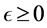. A mapping 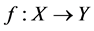is said to be an ò-isometry provided

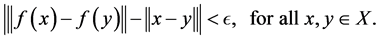
In 1945, Hyers and Ulam proposed the following question: whether for every surjective ò-isometry 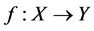with 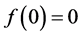there exist a surjective linear isometry 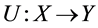and 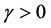such that 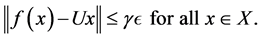After many efforts of a number of mathematicians (see, for instance [14] -[19] ) Omladi and emrl gave the sharp estimate that 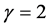in 1995 (see [20] ).

In this section, we ask whether we can discuss the the stability of ò-isometry in operator space category? We try to propose a question and give a little answer.

Firstly, we get the following result.

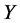Theorem Let and be operator spaces. If a mapping 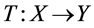satisfies that for any,

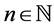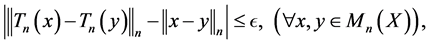
then 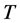is an isometry.

Proof. For any, 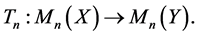Let. Specially, we put

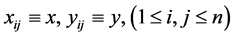, then 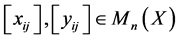and we have

Since

we get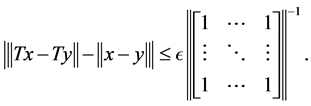

So 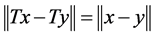holds for any. is an isometry.

Acknowledgements

A part of this work was completed when I visited the University of Illinois, Urbana. I would like to thank Professor Zhong-Jin Ruan for the invitation and great help.

The author also expresses his appreciation to Dr. Liu Rui for many very helpful comments regarding the stability of ò-isometry in operator space category.

Funding

This work is supported by the NSFC grant 11101220, 11271199 and the Fundamental Research Funds for the Central Universities.

References