Advances in Pure Mathematics
Vol.4 No.8(2014), Article
ID:48790,5
pages
DOI:10.4236/apm.2014.48047
Boolean Automorphisms of a Hypercube Coincide with the Linear Isometries
Eberto R. Morgado1, Marco V. José2
1Facultad de Matemática, Física y Computación, Universidad Central “Marta Abreu” de Las Villas, Santa Clara, Cuba
2Theoretical Biology Group, Instituto de Investigaciones Biomédicas, Universidad Nacional Autónoma de México, México D.F., México
Email: morgado@uclv.edu.cu, marcojose@biomedicas.unam.mx
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 June 2014; revised 10 July 2014; accepted 23 July 2014
ABSTRACT
Boolean homomorphisms of a hypercube, which correspond to the morphisms in the category of finite Boolean algebras, coincide with the linear isometries of the category of finite binary metric vector spaces.
Keywords:Boolean Automorphisms, Boolean Algebra, Hypercube, Linear Isometries

1. Introduction
An automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism group. It is, loosely speaking, the symmetry group of the object.
As is well known, a Boolean lattice is a partially ordered set with some special properties of its partial order relation, and it can also be envisaged as an algebraic system with two algebraic binary operations. This algebraic system is the so-called Boolean algebra, associated to the Boolean lattice. The Boolean algebra can also be provided with a ring structure, the so-called Boolean ring, associated to the Boolean lattice. It can even be regarded as a binary vector space, that is, a vector space over the binary field 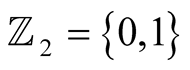 of two elements [1] . These four categories are functorial related by isofunctors that carry over the morphisms of one category over morphisms of the other [2] . The Boolean lattice is also a metric space with the so-called Hamming distance, where the morphisms are the so-called isometries.
of two elements [1] . These four categories are functorial related by isofunctors that carry over the morphisms of one category over morphisms of the other [2] . The Boolean lattice is also a metric space with the so-called Hamming distance, where the morphisms are the so-called isometries.
The aim of the present work is to show that the Boolean homomorphisms, that is, the morphisms in the category of the finite Boolean algebras, are the same to the linear isometries in the category of finite binary vector spaces when the Hamming distance is used.
2. Some Previous Definitions and Concepts
2.1. Definition
Given a Boolean algebra 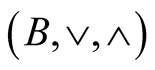 a function
a function  such that
such that 
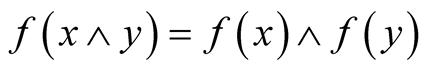 for all x, y of B, and
for all x, y of B, and 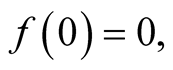
 where 0 and 1 denote the neutral elements of
where 0 and 1 denote the neutral elements of 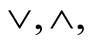 respectively, is called a Boolean endomorphism. If f is bijective, it is called a Boolean automorphism.
respectively, is called a Boolean endomorphism. If f is bijective, it is called a Boolean automorphism.
It is immediate that, for the Boolean addition +, defined as  which provides to B a structure of Abelian group, f is a group endomorphism, or a group authomorphism if it is bijective.
which provides to B a structure of Abelian group, f is a group endomorphism, or a group authomorphism if it is bijective.
It is well known that the triple 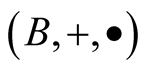 where
where  denotes the obviously defined external operation of the binary field
denotes the obviously defined external operation of the binary field  over B, is a
over B, is a 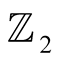 -vector space.
-vector space.
It is not difficult to prove that every group endomorphism of the Abelian group 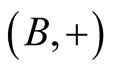 is also a linear endomorphism of the vector space
is also a linear endomorphism of the vector space 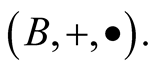
The triplet 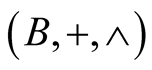 is a unitary commutative ring, such that every element
is a unitary commutative ring, such that every element  is idempotent, that is,
is idempotent, that is, 
It is easy to notice that every Boolean endomorphism is also a unitary ring endomorphism, and conversely, every unitary ring endomorphism is a Boolean endomorphism.
It is also well known that, the binary relation 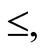 defined as
defined as 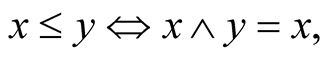 is a partial order relation with minimum and maximum 0 and 1, respectively.
is a partial order relation with minimum and maximum 0 and 1, respectively.
The ordered pair  defines a lattice, such that for every binary subset
defines a lattice, such that for every binary subset 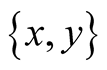 the elements
the elements 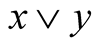 and
and 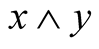 are, respectively, the least upper bound (supremum) and the greatest lower bound (infimum) of the set
are, respectively, the least upper bound (supremum) and the greatest lower bound (infimum) of the set 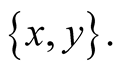
A function  is a Boolean endomorphism if, and only if, it is isotonic with respect to the partial order relation
is a Boolean endomorphism if, and only if, it is isotonic with respect to the partial order relation  that is, if
that is, if 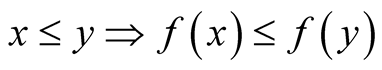 for all x, y of B..
for all x, y of B..
If the vector space 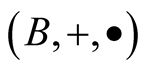 has a finite basis of n elements, we will say that the Boolean algebra
has a finite basis of n elements, we will say that the Boolean algebra  is finite-dimensional, being the number n its dimension.
is finite-dimensional, being the number n its dimension.
It can be proved that every n-dimensional Boolean algebra is isomorphic to the Boolean algebra 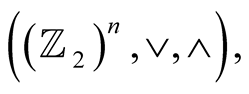 where the operations are bitwise induced by the logic operations of disjunction and conjunction, according to the following Table1
where the operations are bitwise induced by the logic operations of disjunction and conjunction, according to the following Table1
The elements 0 and 1 represent, respectively, falsity or veracity of a proposition. The Boolean algebra 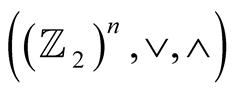 is generally called the n-dimensional hypercube. It is due to the fact that in the case
is generally called the n-dimensional hypercube. It is due to the fact that in the case  the triplets of zeros and ones are the algebraic representations of the vertexes of a cube, inserted, as a subset, in the 3-dimensional
the triplets of zeros and ones are the algebraic representations of the vertexes of a cube, inserted, as a subset, in the 3-dimensional 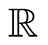 -vector space
-vector space  being
being 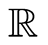 the field of real numbers.
the field of real numbers.
2.2. The Inner Product in the Hypercube 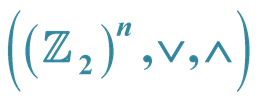
2.2.1. Definition
For two n-tuples 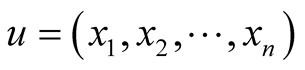 and
and 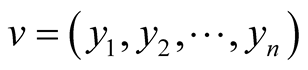 of
of  we call scalar product or inner product of u with v the number
we call scalar product or inner product of u with v the number  where the addition and the multiplication are the ordinary operations in the ring
where the addition and the multiplication are the ordinary operations in the ring 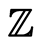 of integers.
of integers.
This inner product is the restriction to the set  of the ordinary inner product of the Euclidean n-dimensional
of the ordinary inner product of the Euclidean n-dimensional  -vector space
-vector space 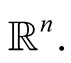
If the column matrices 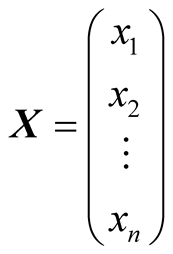 and
and 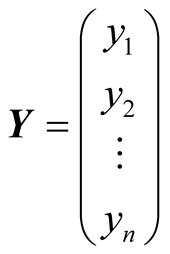 are the matrix representation of the n-tuples u and v, respectively, the inner product
are the matrix representation of the n-tuples u and v, respectively, the inner product 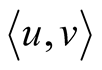 can be expressed as the matrix product
can be expressed as the matrix product 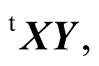 where
where  denotes the transpose matrix of X, that is, the row matrix
denotes the transpose matrix of X, that is, the row matrix 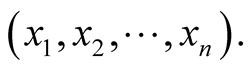
2.2.2. Definition
For a vector 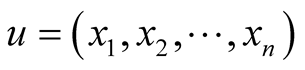 we call the norm, absolute value, or weight of u, the inner product
we call the norm, absolute value, or weight of u, the inner product 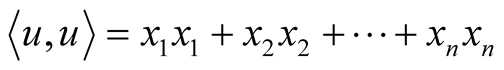 of u with itself, denoted as
of u with itself, denoted as 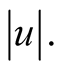 Obviously, the norm
Obviously, the norm 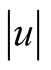 is equal to the number of times the number 1 is a component of u.
is equal to the number of times the number 1 is a component of u.
It is not difficult to notice that the inner product  of the vector u and v, is equal to the norm of the vector product
of the vector u and v, is equal to the norm of the vector product 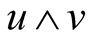 in the Boolean ring
in the Boolean ring 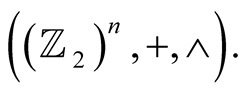
A vector u of norm 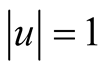 is called unitary vector. The only unitary vectors are
is called unitary vector. The only unitary vectors are
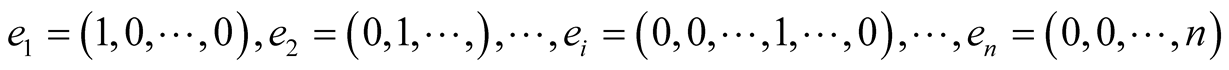 and they conform the so-called canonical basis
and they conform the so-called canonical basis 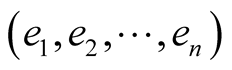 of the binary vector space
of the binary vector space 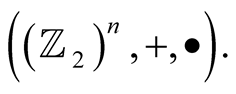
3. The Concept of Orthogonality
wang#_2title:spDefinition
We say that two vectors u and v are orthogonal or perpendicular if the inner product  is equal to 0.
is equal to 0.
4. The Hamming Distance in the Hypercube
wang#_2title:spDefinition
For two vectors u and v, we define the Hamming distance between them, as the norm 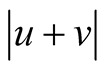 of their Boolean addition. Obviously, it is equal to the number of places where the components of both vectors are different.
of their Boolean addition. Obviously, it is equal to the number of places where the components of both vectors are different.
5. Linear Isometries of the Hypercube
Definition
A function  is called an isometry if it preserves the distance between points, that is, if
is called an isometry if it preserves the distance between points, that is, if
 for all
for all 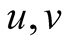 of the set.
of the set.
If the isometry f is also a linear transformation, then, the matrix A of f, with respect to the canonical basis 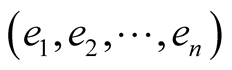 is an orthogonal matrix, that is, such that
is an orthogonal matrix, that is, such that 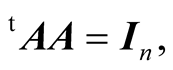 the identity
the identity 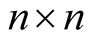 matrix.
matrix.
It is clear that a linear isometry also preserves the absolute value of any vector and the inner product of any two vectors.
The hypercube 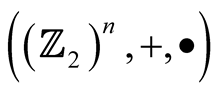 can also be envisaged as a graph, where the vertexes or nodes are the n-tuplesand the edges are the binary subsets
can also be envisaged as a graph, where the vertexes or nodes are the n-tuplesand the edges are the binary subsets 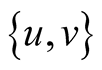 such that the distance
such that the distance  is equal to 1. Two vectors u and v of an edge
is equal to 1. Two vectors u and v of an edge 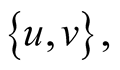 that is, such that
that is, such that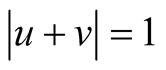 , are called adjacent points of the hypercube.
, are called adjacent points of the hypercube.
It can be proved that the Hamming distance between two points u and v is equal to the minimal length of a path between them, that is, the minimal number of edges for going from one to the other.
6. Main Results
6.1. Lemma
In the hypercube  the only set of n non-null vectors, which are pairwise orthogonal, is the set
the only set of n non-null vectors, which are pairwise orthogonal, is the set 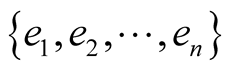 of the unitary canonical vectors.
of the unitary canonical vectors.
Proof: (Induction over n)
For n = 2 the assertion is trivially true.
Let us suppose that it is true for every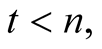 , being
, being 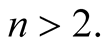
Let 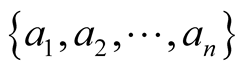 be a set of non-null and pairwise orthogonal vectors in the hypercube
be a set of non-null and pairwise orthogonal vectors in the hypercube  To prove that they are all unitary vectors let us suppose that one of them, say a1 is not unitary, that is of norm
To prove that they are all unitary vectors let us suppose that one of them, say a1 is not unitary, that is of norm 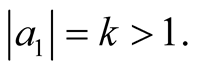 Then, the vectors
Then, the vectors 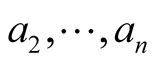 belong to the
belong to the 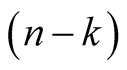 -dimensional vector subspace, which is the supplementary orthogonal vector subspace of the line
-dimensional vector subspace, which is the supplementary orthogonal vector subspace of the line  As the vectors
As the vectors 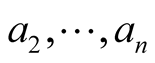 are linearly independent, then
are linearly independent, then 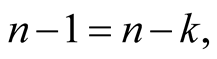 then
then  in contradiction with the assumption
in contradiction with the assumption 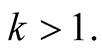 Hence, all the vectors of the set are unitary, as we wanted to show.
Hence, all the vectors of the set are unitary, as we wanted to show.
Now, we are in conditions to carry out the proof of the following.
6.2. Theorem
A function f is a Boolean automorphism if, and only if, it is a linear isometry.
Proof: If f is a Boolean automorphism it means that 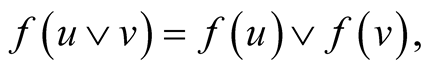
 for all u, v of
for all u, v of 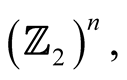 and
and 
Then, 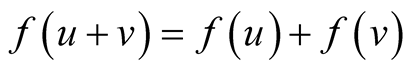 for the Boolean addition + such that,
for the Boolean addition + such that,  Hence, f is a linear transformation of the vector space.
Hence, f is a linear transformation of the vector space.
For canonical vectors 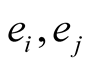 we have that
we have that 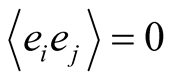 if
if , and
, and 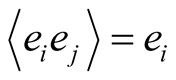 if
if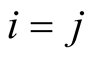 , which means that they are unitary and pairwise orthogonal. From this, we have that
, which means that they are unitary and pairwise orthogonal. From this, we have that 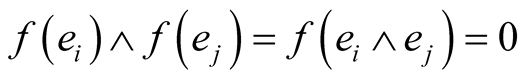 if
if 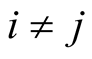 and
and 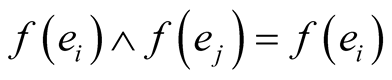 if
if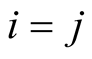 . Then, the vectors
. Then, the vectors 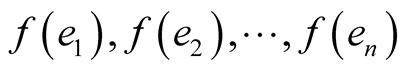 are pairwise orthogonal and, from the lemma, they are unitary vectors. Hence, the linear function f is a permutation of the canonical basis
are pairwise orthogonal and, from the lemma, they are unitary vectors. Hence, the linear function f is a permutation of the canonical basis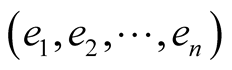 . Then, the matrix A of f, with respect to this basis, is orthogonal, that is, such that
. Then, the matrix A of f, with respect to this basis, is orthogonal, that is, such that 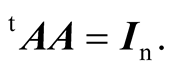 Then, f is a linear isometry of the space, as we wanted to prove.
Then, f is a linear isometry of the space, as we wanted to prove.
Conversely, if f is a Boolean isometry,  for all i and j, then for
for all i and j, then for
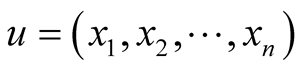 and
and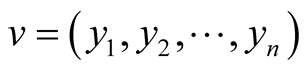 ,
, 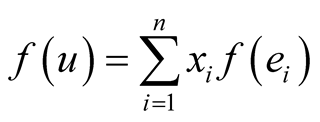 ,
,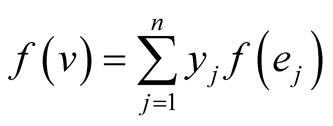 .
.
Then, 
On the other hand, it is known that 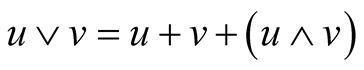 for all u and v. Then,
for all u and v. Then,
 .
.
Then, we have proved that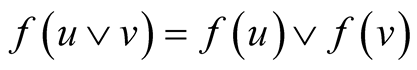 ,
, 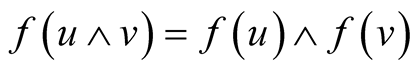 for all u, v elements of the space.
for all u, v elements of the space.
As f is linear we have 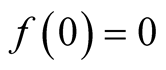 and as for every u,
and as for every u,  we obtain that
we obtain that 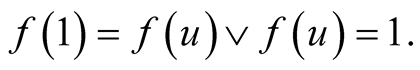
Then, we have proved that f is a Boolean homomorphism.
7. Concluding Remarks
In this work we have demonstrated that Boolean automorphisms of a hypercube are the same to the linear isometries of finite binary metric spaces taking as a metric the Hamming distance. This fundamental result becomes of much interest when characterizing the symmetry groups of polytopes [3] . The use of the theory of categories imparts novel insights for understanding and generalizing the symmetries of any object. This result is of interest in many areas of research. For example, the representation of the Universal Genetic Code as a 6-dimensional hypercube [4] [5] has permitted to study its evolution by a series of successive symmetry breakings [6] .
Acknowledgements
MVJ was financially supported by PAPIIT-IN107112, UNAM, México.
References
- Dubreil, P. and Jacotin, M.L. (1961) Lecciones de Algebra Moderna. Editorial Dunod, Francia.
- Mitchell, B. (1965) Theory of Categories. Academic Press, New York.
- Coxeter, H.S.M. (1973) Regular Polytopes. 3rd Edition. Dover Publication Inc., New York.
- José, M.V., Morgado, E.R. and Govezensky, T. (2007) An Extended RNA Code and Its Relationship to the Standard Genetic Code: An Algebraic and Geometrical Approach. Bulletin of Mathematical Biology, 69, 215-243. http://dx.doi.org/10.1007/s11538-006-9119-3
- José, M.V., Morgado, E.R., Sánchez, R. and Govesenky, T. (2012) The 24 Possible Algebraic Representations of the Standard Genetic Code in Six or in Three Dimensions. Advanced Studies in Biology, 4, 119-152.
- José, M.V., Govesenky, T., García, J.A. and Bobadilla, J.R. (2009) On the Evolution of the Standard Genetic Code: Vestiges of Critical Scale Invariance from the RNA World to Current Prokaryote Genomes. PLoS ONE, 4, e4340.http://dx.doi.org/10.1371/journal.pone.0004340


