Advances in Pure Mathematics
Vol.4 No.2(2014), Article ID:43123,5 pages DOI:10.4236/apm.2014.42006
A New Characterization of Totally Umbilical Hypersurfaces in de Sitter Space
1College of Mathematics and Information Science, Henan Normal University, Xinxiang, China
2School of Mathematics and Statistics, Nangyang Normal University, Nangyang, China
3Department of Computer Science, Henan Normal University, Xinxiang, China
Email: caolf2010@yahoo.com
Copyright © 2014 Linfen Cao et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Linfen Cao et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 4, 2013; revised December 4, 2013; accepted December 11, 2013
Keywords: de Sitter Space; Spacelike Hypersurface; Higher Order Mean Curvatures
ABSTRACT
It is shown that a compact spacelike hypersurface which is contained in the chronological future (or past) of an equator of de Sitter space is a totally umbilical round sphere if the kth mean curvature function Hk is a linear combination of Hk+1,∙∙∙, Hn. This is a new angle to characterize round spheres.
1. Introduction
Let 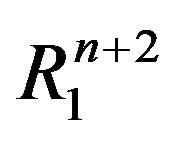 be the (n + 2)-dimensional Lorentz-Minkowski space, namely, the real vector space
be the (n + 2)-dimensional Lorentz-Minkowski space, namely, the real vector space  endowed with the Lorentzian inner product
endowed with the Lorentzian inner product  given by
given by
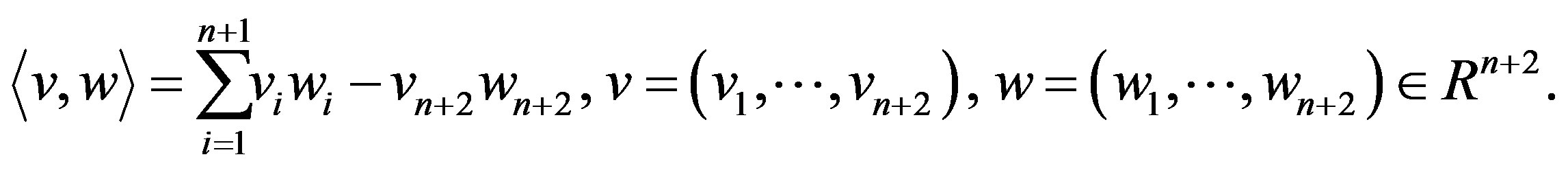
Then the n-dimensional de Sitter space is defined by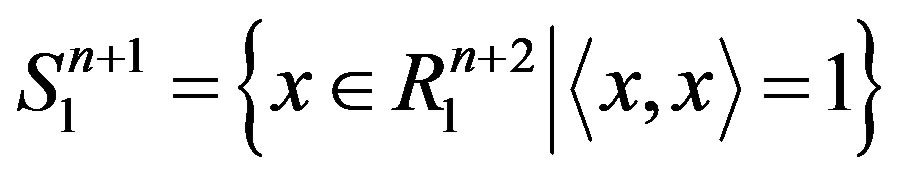 . It is well known that, for
. It is well known that, for  the de Sitter space
the de Sitter space  is the standard simply connected Lorentzian space form of positive constant sectional curvature. A smooth immersion
is the standard simply connected Lorentzian space form of positive constant sectional curvature. A smooth immersion 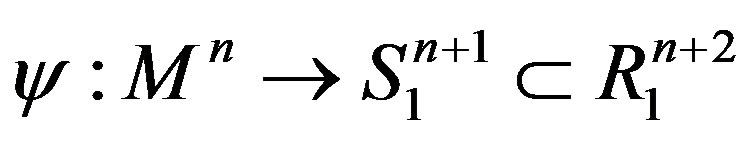 of an
of an  -dimensional connected manifold
-dimensional connected manifold  is said to be a spacelike hypersurface if the induced metric via
is said to be a spacelike hypersurface if the induced metric via 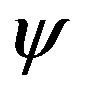 is a Riemannian metric on
is a Riemannian metric on , which, as usual, is also denoted by
, which, as usual, is also denoted by .
.
The interest for the study of spacelike hypersurfaces in de Sitter space is motivated by the fact that such hypersurfaces exhibit nice Bernstein-type properties. In 1977, Goddard [1] conjectured that the only complete spacelike hypersurfaces with constant mean curvature in  should be the totally umbilical ones. This conjecture motivated the work of an important number of authors who considered the problem of characterizing the totally umbilical spacelike hypersurfaces of de Sitter space. In [2], Montiel showed that the only compact spacelike hypersurfaces in
should be the totally umbilical ones. This conjecture motivated the work of an important number of authors who considered the problem of characterizing the totally umbilical spacelike hypersurfaces of de Sitter space. In [2], Montiel showed that the only compact spacelike hypersurfaces in  with constant mean curvature
with constant mean curvature 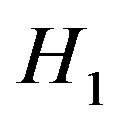 were the totally umbilical round spheres. More recently, Cheng and Ishikawa [3] have shown that the totally umbilical round spheres are the only compact spacelike hypersurfaces in de Sitter space with constant scalar curvature
were the totally umbilical round spheres. More recently, Cheng and Ishikawa [3] have shown that the totally umbilical round spheres are the only compact spacelike hypersurfaces in de Sitter space with constant scalar curvature .
.
The natural generalization of mean and scalar curvature for a spacelike hypersurface in de Sitter space are the kth mean curvature 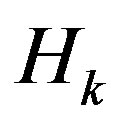 for
for . Actually,
. Actually, 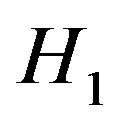 is the mean curvature and
is the mean curvature and  is, up to a constant, the scalar curvature of the hypersurface. In [4], Aledo, jointly with Alias and Romero, developed some integral formulas for compact spacelike hypersurfaces in
is, up to a constant, the scalar curvature of the hypersurface. In [4], Aledo, jointly with Alias and Romero, developed some integral formulas for compact spacelike hypersurfaces in  and applied them in order to characterize the totally umbilical round spheres of
and applied them in order to characterize the totally umbilical round spheres of .
.
Theorem 1([4], Theorem 7) Let  be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of
be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of . If
. If 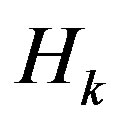 is constant for some
is constant for some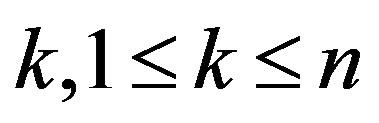 , then
, then  is a totally umbilical round sphere.
is a totally umbilical round sphere.
Since  by definition, the result above can be read as follows: if
by definition, the result above can be read as follows: if  is constant for some
is constant for some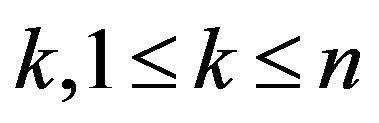 , then
, then  is a totally umbilical round sphere. In [5], Alias extended Theorem 1 in the following way.
is a totally umbilical round sphere. In [5], Alias extended Theorem 1 in the following way.
Theorem 2 ([5]) Let 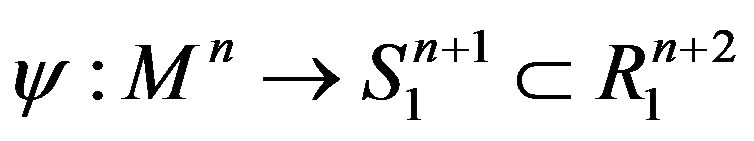 be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of
be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of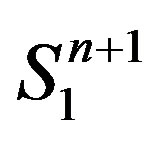 . If
. If 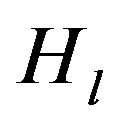 does not vanish on
does not vanish on  and the ratio
and the ratio 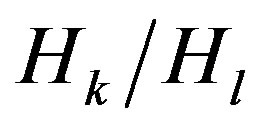 is constant for some
is constant for some , then
, then 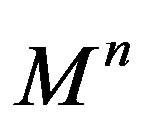 is a totally umbilical round sphere.
is a totally umbilical round sphere.
In [6] the authors considered that 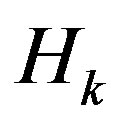 is the linear combination of
is the linear combination of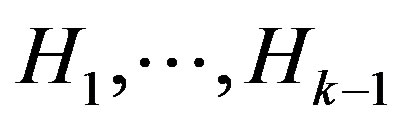 , and proved:
, and proved:
Theorem 3 ([6]) Let 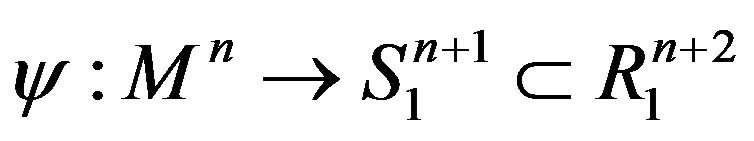 be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of
be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of . If there are nonnegative constants
. If there are nonnegative constants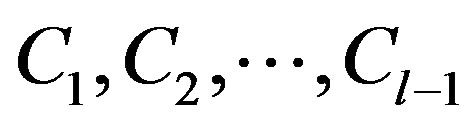 , at least one
, at least one 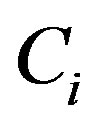 is positive, such that
is positive, such that  holds on
holds on , then
, then 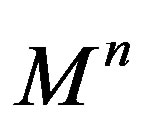 is a totally umbilical round sphere.
is a totally umbilical round sphere.
In this paper, we will show another characterization of totally umbilical round sphere, which extends Theorems 1 and 2 above.
Theorem 4 Let 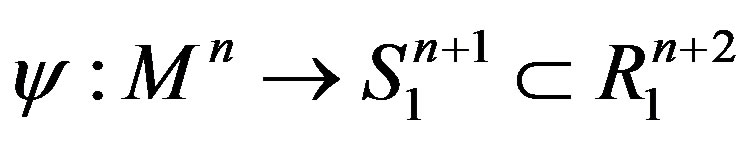 be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of
be a compact spacelike hypersurface in de Sitter space which is contained in the chronological future (or past) of an equator of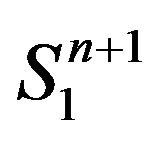 . If
. If  does not vanish on
does not vanish on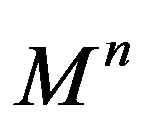 Ÿ for some fixed
Ÿ for some fixed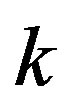 ,
, 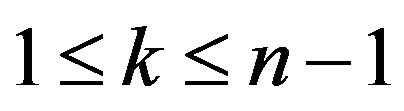 , there exist constants
, there exist constants  such that
such that
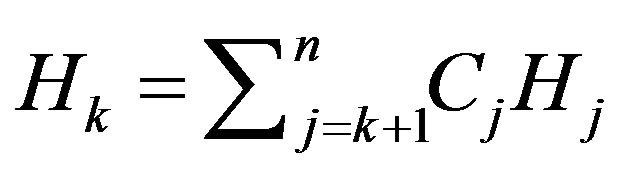 on
on , then
, then 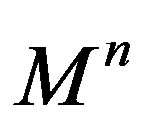 is a totally umbilical round sphere.
is a totally umbilical round sphere.
Ÿ there are 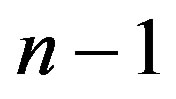 constants
constants 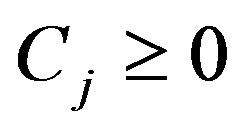 such that
such that 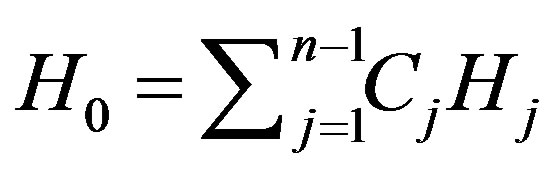 on
on , then
, then  is a totally umbilical round sphere.
is a totally umbilical round sphere.
Ÿ Remark.
Ÿ Note in some special cases the condition  does not vanish should can be dropped, for examples, only one coefficient
does not vanish should can be dropped, for examples, only one coefficient  case. However in general cases we can not drop it now.
case. However in general cases we can not drop it now.
Ÿ The corresponding theorem characterizes ellipsoids also holds in affine differential geometry.
2. Preliminaries
Throughout this paper we will deal with compact spacelike hypersurfaces in de Sitter space. Recall that every compact spacelike hypersurfaces 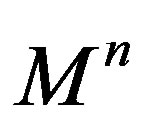 in
in  is diffeomorphic to an n-sphere [4] and, in particular, it is orientable. Then, there exists a timelike unit normal field
is diffeomorphic to an n-sphere [4] and, in particular, it is orientable. Then, there exists a timelike unit normal field  globally defined on
globally defined on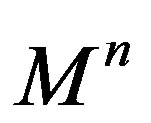 . We will refer to
. We will refer to 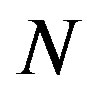 as the Gauss map of the immersion and we will say that
as the Gauss map of the immersion and we will say that 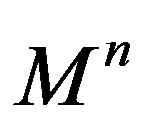 is oriented by
is oriented by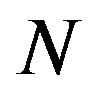 .
.
We will denote by  the shape operator of
the shape operator of 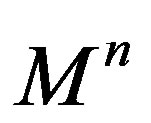 in
in  with respect to
with respect to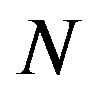 , which is given by
, which is given by

Associated to the shape operator of 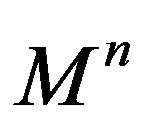 there are
there are 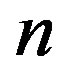 algebraic invariants, which are the elementary symmetric functions
algebraic invariants, which are the elementary symmetric functions 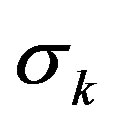 of its principal curvatures
of its principal curvatures  given by
given by
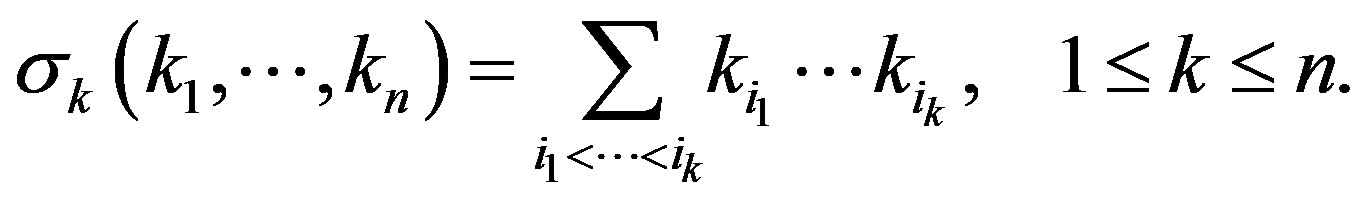
The kth mean curvature 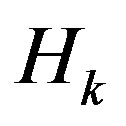 of the spacelike hypersurfaces is then defined by
of the spacelike hypersurfaces is then defined by
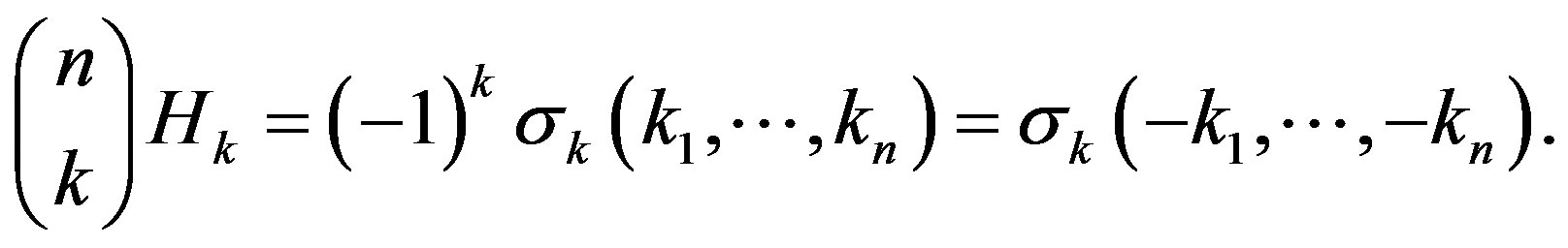
When 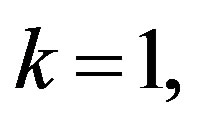
 is the mean curvature of
is the mean curvature of . On the other hand, when
. On the other hand, when 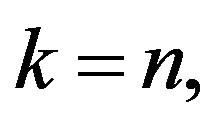
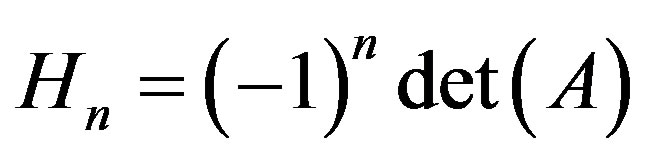 defines the Gauss-Kronecker curvature of the spacelike hypersurface, and for
defines the Gauss-Kronecker curvature of the spacelike hypersurface, and for 
 is, up to a constant, the scalar curvature
is, up to a constant, the scalar curvature  of
of , since
, since  (for details see [4]).
(for details see [4]).
The proof of our theorem makes an essential use of the following integral formulas for compact spacelike hypersurfaces in , which is developed in [4].
, which is developed in [4].
Lemma 5 (Minkowski formulas) Let 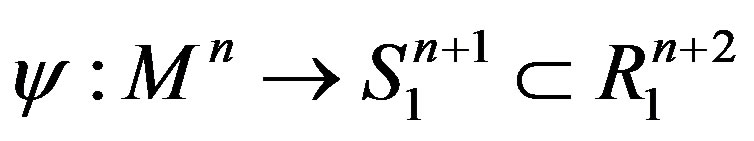 be a compact spacelike hypersurface immersed into de Sitter space and let
be a compact spacelike hypersurface immersed into de Sitter space and let  a fixed arbitrary vector. For each
a fixed arbitrary vector. For each 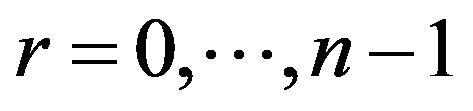 the following formula holds:
the following formula holds:
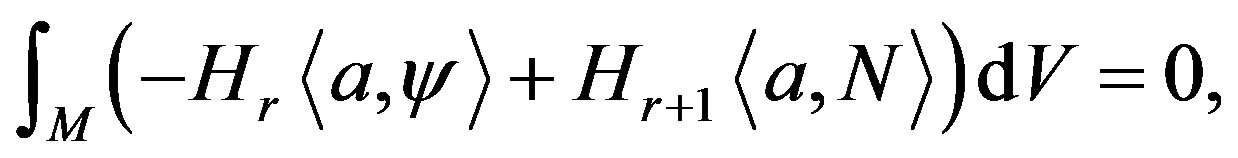
where 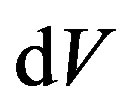 is the n-dimensional volume element of
is the n-dimensional volume element of 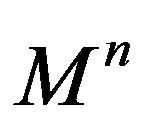 with respect to the induced metric and the chosen orientation.
with respect to the induced metric and the chosen orientation.
3. Proof of the Theorem 4
Let us assume, for instance, that the hypersurface  is contained in the future of the equator determined by a unit timelike vector
is contained in the future of the equator determined by a unit timelike vector 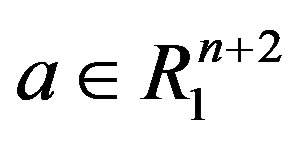 (the case of the past is similar). That means that
(the case of the past is similar). That means that

Let us orient  by the Gauss map
by the Gauss map 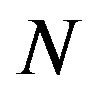 which is in the same time-orientation as
which is in the same time-orientation as , so that
, so that  Since the height function
Since the height function 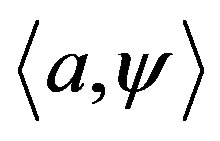 is negative on
is negative on , by compactness there exists a point
, by compactness there exists a point 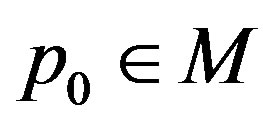 where it attains its maximum
where it attains its maximum
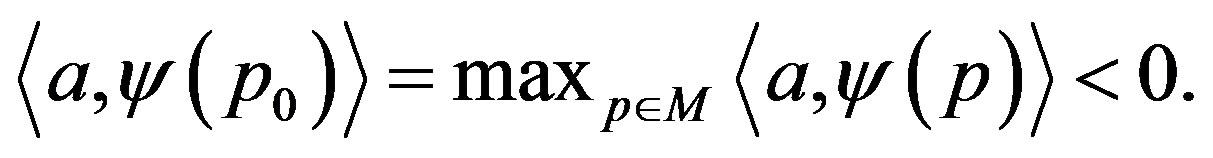
Therefore, its gradient vanishes at that point, 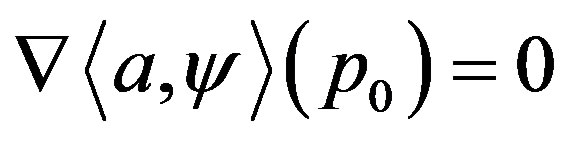 , and its Hessian satisfies
, and its Hessian satisfies
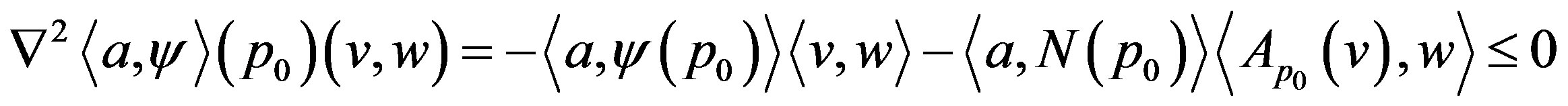
for all 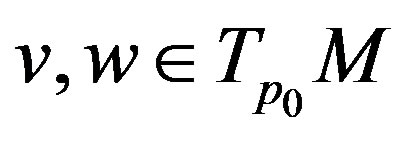 (for the details see the proof of Theorem 7 in [4]). On the other hand, since
(for the details see the proof of Theorem 7 in [4]). On the other hand, since
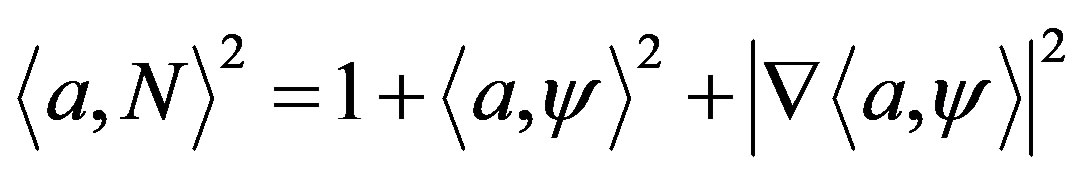
and
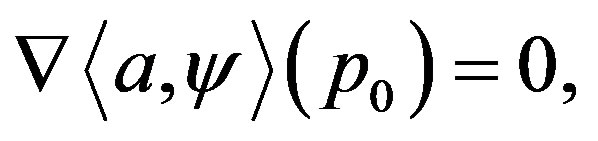
then

Therefore, choosing 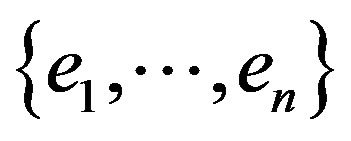 a basis of principal directions at the point
a basis of principal directions at the point 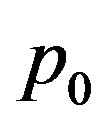 we conclude that
we conclude that
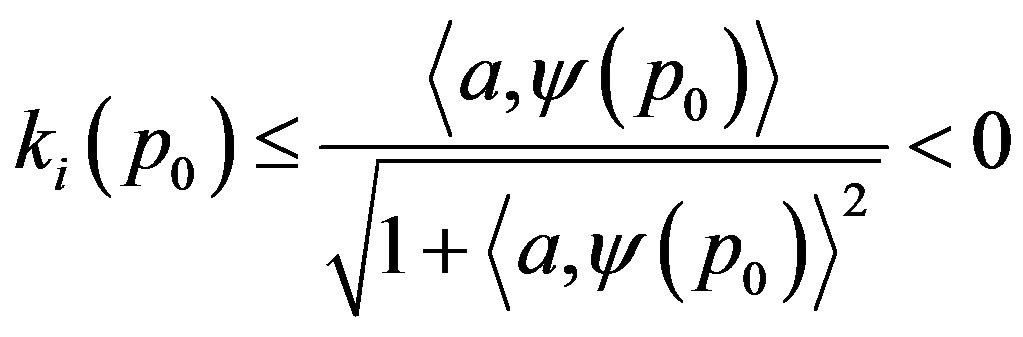 (1)
(1)
for each 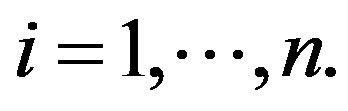 In particular,
In particular,  are positive. The mean curvature functions
are positive. The mean curvature functions  is positive on
is positive on  (recall that
(recall that  does not vanish on
does not vanish on  by assumption). Therefore, from the proof of Lemma 1 in [7] and taking into account the sign convention in our definition of the higher order mean curvature, it follows that every
by assumption). Therefore, from the proof of Lemma 1 in [7] and taking into account the sign convention in our definition of the higher order mean curvature, it follows that every 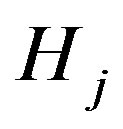 is positive for
is positive for 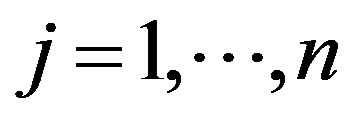 and
and
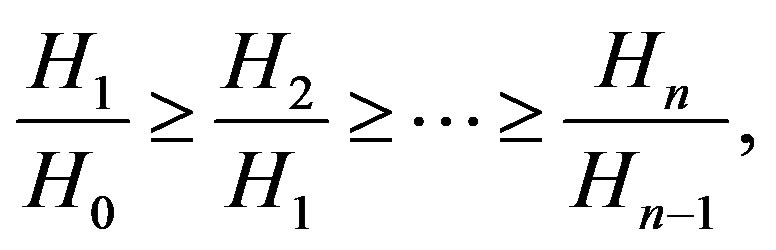 (2)
(2)
with equality at any stage only at umbilical points.
Let us start proving the first statement of Theorem 4. Using
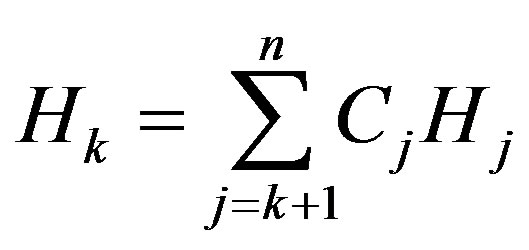
and the Minkowski formulae, we have
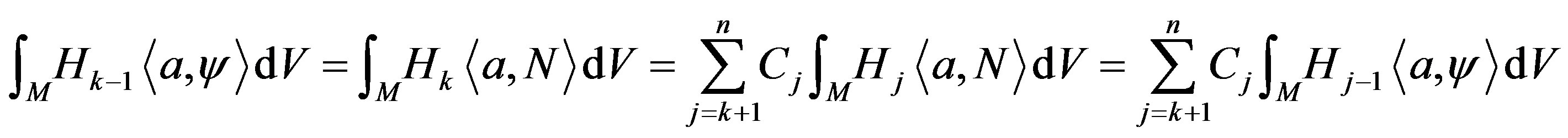
That is,
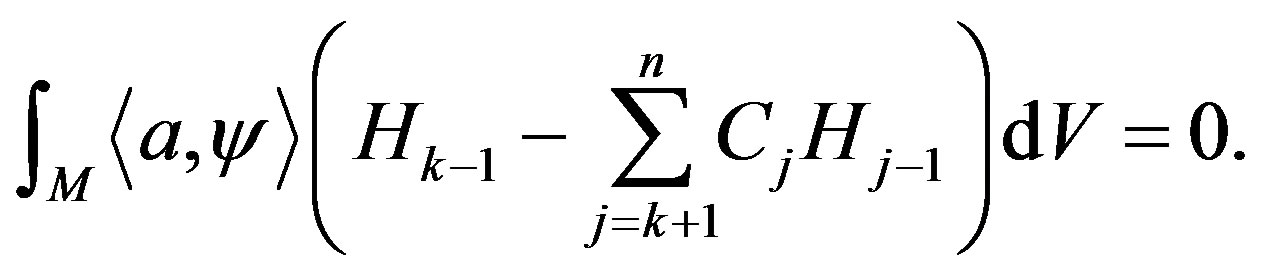
Now we claim that
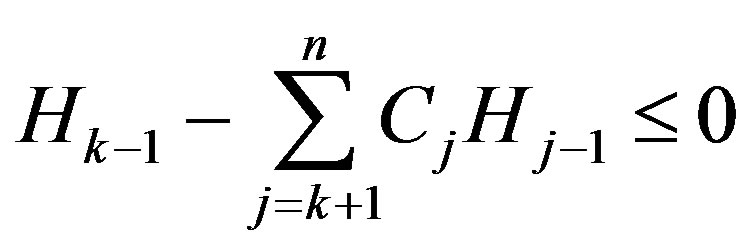 (3)
(3)
on , with equality if and only if
, with equality if and only if . Assume that (3) is true. Then, since
. Assume that (3) is true. Then, since 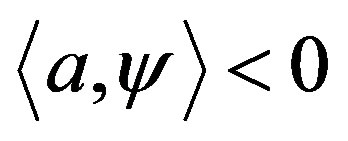 on
on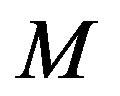 , we conclude that
, we conclude that

which implies that  is an totally umbilical round sphere.
is an totally umbilical round sphere.
It remains to prove (3). Using the assumption of theorem 4, that is  and (2), we have
and (2), we have
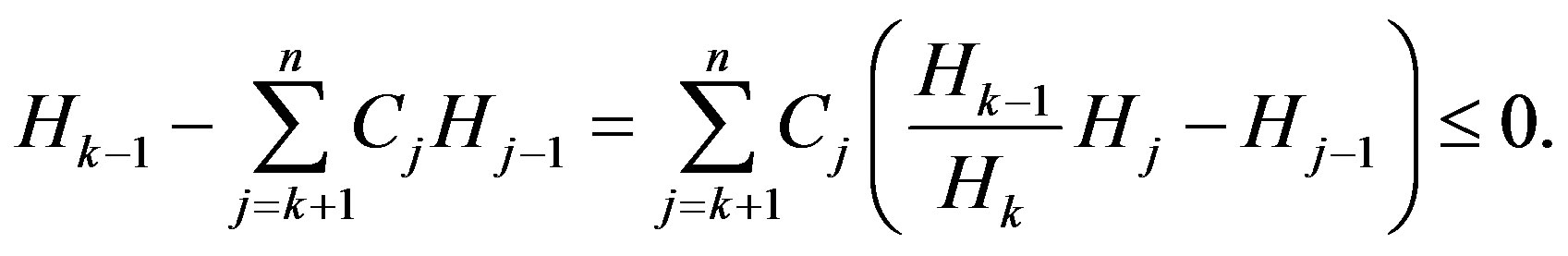 (4)
(4)
Now we prove the second statement. Using
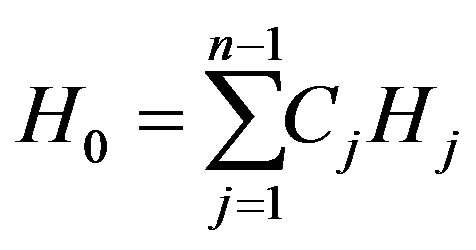
and the Minkowski formulae, we have

That is,

Now we claim that
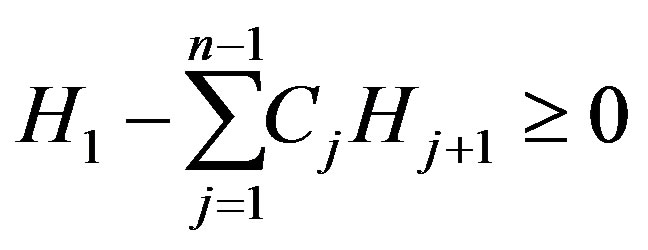 (5)
(5)
on , with equality if and only if
, with equality if and only if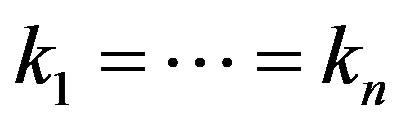 . Assume that (5) is true. Then, since
. Assume that (5) is true. Then, since  on
on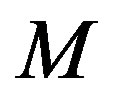 , we conclude that
, we conclude that
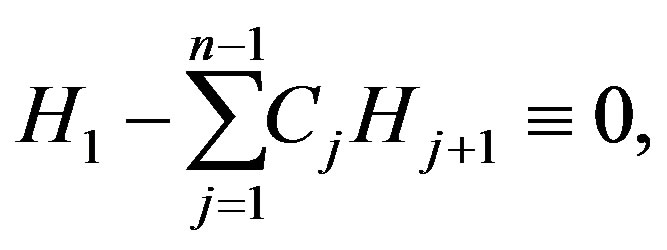
which implies that 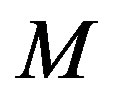 is an totally umbilical round sphere. It remains to prove (5). As in the first proof, using the assumption of theorem 4, that is
is an totally umbilical round sphere. It remains to prove (5). As in the first proof, using the assumption of theorem 4, that is , and (2) we known
, and (2) we known
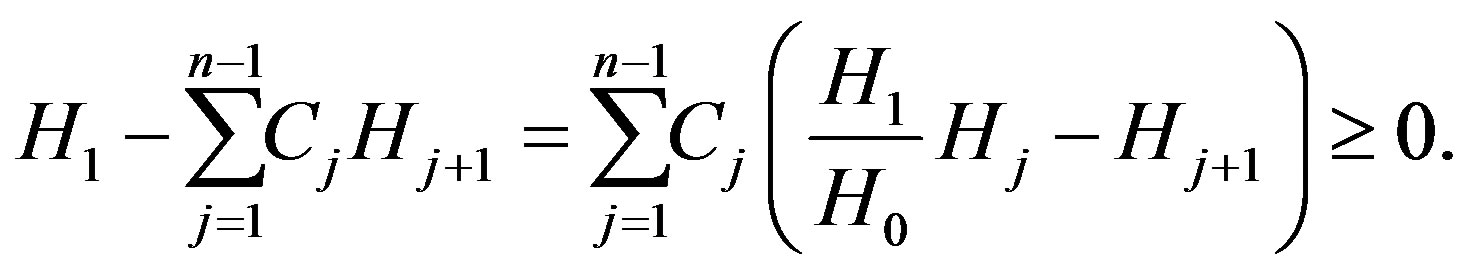
This completes the proof of the Theorem 4.
Funding
This work is supported by grant (No.U1304101 and 11171091) of NSFC and NSF of Henan Province (No.132300410141).
REFERENCES
[1] A. J. Goddard, “Some Remarks on the Existence of Spacelike Hypersurfaces of Constant Mean Curvature,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 82, 1977, pp. 489-495. http://dx.doi.org/10.1017/S0305004100054153
[2] S. Montiel, “An Integral Inequality for Compact Spacelike Hypersurfaces in de Sitter Space and Applications to the Case of Constant Mean Curvature,” Indiana University Mathematics Journal, Vol. 37, No. 4, 1988, pp. 909-917. http://dx.doi.org/10.1017/S0305004100054153
[3] Q.-M. Cheng and S. Ishikawa, “Spacelike Hypersurfaces with Constant Scalar Curvature,” Manuscripta Mathematica, Vol. 95, No. 4, 1998, pp. 499-505. http://dx.doi.org/10.1007/s002290050043
[4] J. A. Aledo, L. J. Alias and A. Romero, “Integral Formulas for Compact Space-Like Hypersurfaces in de Sitter Space: Applications to the Case of Constant Higher Mean Curvature,” Journal of Geometry and Physics, Vol. 31, No. 2-3, 1999, pp. 195-208. http://dx.doi.org/10.1016/S0393-0440(99)00008-X
[5] L. J. Alias and S.-E. Koh, “Remarks on Compact Spacelike Hypersurfaces in de Sitter Space with Constant Higher Order Mean Curvature,” Journal of Geometry and Physics, Vol. 39, No. 1, 2001, pp. 45-49. http://dx.doi.org/10.1016/S0393-0440(00)00073-5
[6] S.-E. Koh and M. S. Yoo, “A Characterization of Totally Umbilical Hypersurfaces in de Sitter Space,” Journal of Geometry and Physics, Vol. 51, No.1, 2004, pp. 34-39. http://dx.doi.org/10.1016/j.geomphys.2003.09.006
[7] S. Montiel and A. Ros, “Compact Hypersurfaces: The Alexandrov Theorem for Higher Order Mean Curvatures,” In: B. Lawson and K. Tenenblat, Eds., Differential Geometry, Longman, Essex, 1991, pp. 279-296.
[8] K. Akutagawa, “On Spacelike Hypersurfaces with Constant Mean Curvature in the de Sitter Space,” Mathematische Zeitschrift, Vol. 196, No. 1, 1987, pp. 13-19. http://dx.doi.org/10.1007/BF01179263
[9] L. J. Alias and A. G. Colares, “A Further Characterization of Ellipsoids,” Results in Mathematics, Vol. 48, No.1-2, 2005, pp. 1-8. http://dx.doi.org/10.1007/BF03322891
[10] H. Li, “Global Rigidity Theorems of Hypersurfaces,” Arkiv for Matematik, Vol. 35, No. 2, 1997, pp. 327-351.
[11] J. Ramanathan, “Complete Spacelike Hypersurfaces of Constant Mean Curvature in de Sitter Space,” Indiana University Mathematics Journal, Vol. 36, No. 2, 1987, pp. 349-359. http://dx.doi.org/10.1512/iumj.1987.36.36020
[12] Y. Zheng, “On Space-Like Hypersurfaces in the de Sitter Space,” Annals of Global Analysis and Geometry, Vol.13, No. 4, 1995, pp. 317-321. http://dx.doi.org/10.1007/BF00773403
[13] Y. Zheng, “Space-Like Hypersurfaces with Constant Scalar Curvature in the de Sitter Space,” Differential Geometry and Its Applications, Vol. 6, No. 1, 1996, pp. 51-54. http://dx.doi.org/10.1016/0926-2245(96)00006-X

