Advances in Pure Mathematics
Vol.3 No.9(2013), Article ID:40798,6 pages DOI:10.4236/apm.2013.39094
Numerical Simulation of Fluid-Structure Interaction Method on Dynamic Movement of Leukocyte in Flow Chamber
School of Mechanical Engineering, Tianjin University, Tianjin, China
Email: liwenjiao@tju.edu.cn
Copyright © 2013 Wenjiao Li. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 13, 2013; revised November 15, 2013; accepted November 25, 2013
Keywords: Fluid-Structure Interaction; Leukocyte; Jumping; Rolling
ABSTRACT
Biomechanical properties of cells play a very important role in regulating cells function. Experimental studies found that when Leukocytes move near the vessel wall, the phenomena such as rolling, jumping and adhesion will appear. Based on the non-linear fluid-structure interaction theory, leukocyte’s tiny jumping mechanism and rolling phenomenon were studied. The results were: 1) The choice of time step of leukocyte had a great influence on the movement of leukocyte. Instead of landing on the bottom of flow chamber, leukocyte jumped to a certain height and then moved periodically toward the bottom of the flow chamber again. Leukocyte had the biggest deformation when jumping; 2) Adhesion and rolling along the bottom of the flow chamber appeared in the process of moving forward, the scrolling speed was greater than that of pure rolling. Leukocytes’ movement in blood vessels was closely related with body physiological and pathological characteristics. The study of dynamic movement of leukocyte provided theoretical basis for clinical medicine.
1. Introduction
Leukocyte, also named as immune cells, is spherical. It deforms easily and charged with a lot of responsibilities. Besides swallowing foreign body, it has immunity to disease resistance. In recent years, Leukocyte’s movement under shear flow is popular. More and more schoolars focus on the transmission mechanism.
Early studies have achieved many useful results in the field of cell movement and deformation. Goldsmith et al. [1] discovered that near the vessel wall leukocyte’s adhesion and jumping phenomena will appear. In 2000, T. Yamaguchi et al. [2] simulated the movement of cells using three-dimensional computational fluid dynamics. The cell model can be adopted by the random rotation, deformation, the migration and proliferation. The cell configuration changes fluid calculation based on infinitesimal. K. C. Chang et al. [3] pointed out that there are three kinds of cell adhesion: firm adhesive, transient adhesive (rolling) and no adhesive. They also found that the unstressed dissociation rate and the bond interaction length are the most important molecular properties to control the dynamics of adhesion. In 2003, M. J. Slattery and C. Dong [4] studied human melanoma cell adhesion and migration in response to stimulation by soluble collagen IV using a modified Boyden chamber. The study of N. A. N’Dri et al. [5] showed that cell rheological properties have significant effects on the adhesion process contrary to what has been hypothesized in most literature. S. Liang et al. [6] provided a rationale and mechanistic basis for understanding of leukocyte-tumor cell interactions under flow conditions during tumor cell extravasation and metastasis. Based on the limited blood flow dynamoics, A. Sequeira et al. [7] adopted the lattice Boltzmann model to study the dynamic change of white blood cells within micro-vessels, which showed that the movement greatly depended on the white blood cell velocity and endothelial wall attraction. In 2010, the lattice Boltzmann method combined with the immersed boundary method to simulate red blood cell movement in microvessel was presented [8]. In previous studies, cells are always assumed to be rigid and solid deformation was not considered. In this study, we analyzed the movement of a single leukocyte in the flow chamber through numerical simulation of fluid-structure interaction method.
2. Materials and Methods
2.1. Equations
The fluid-structure interaction analysis is based on the governing equations of hydrodynamics, governing equations of solid mechanics and the coupling equation.
The governing equation for the fluid domain is Mass conservation equation and momentum conservation equation, which were listed as following
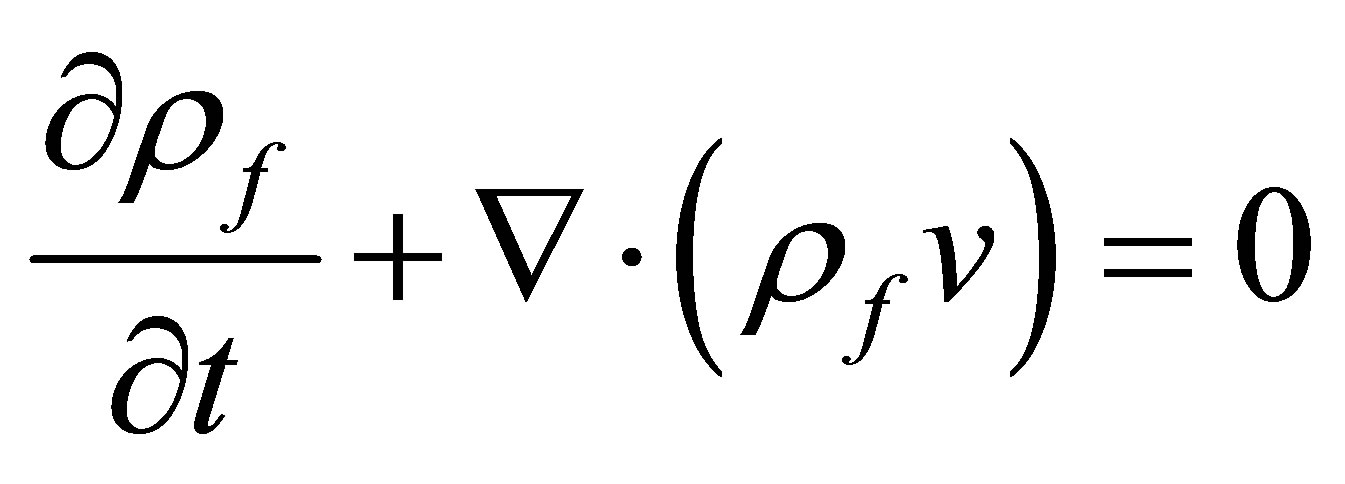 (1)
(1)
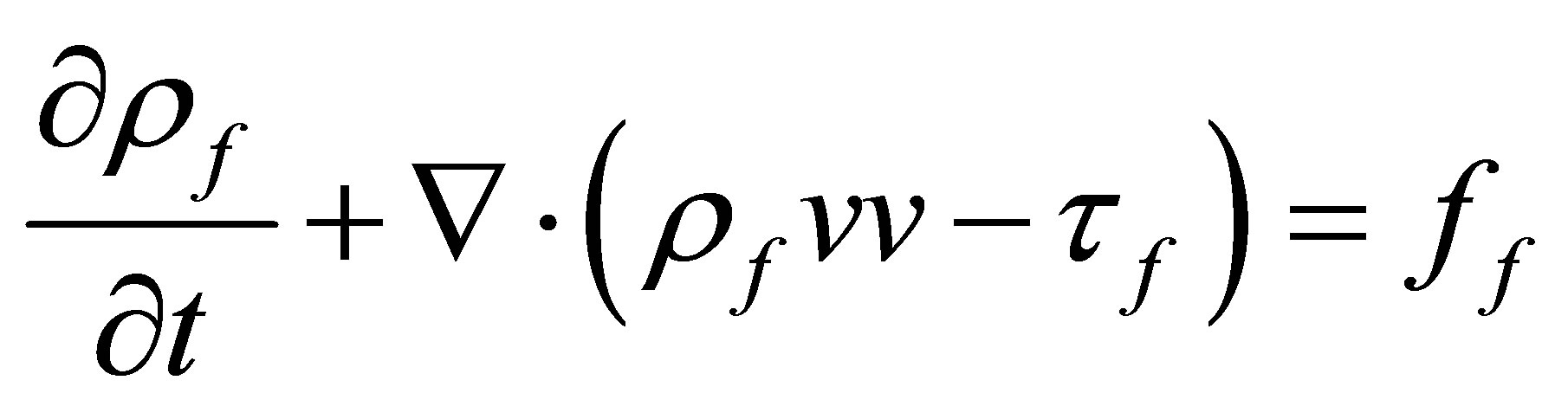 (2)
(2)
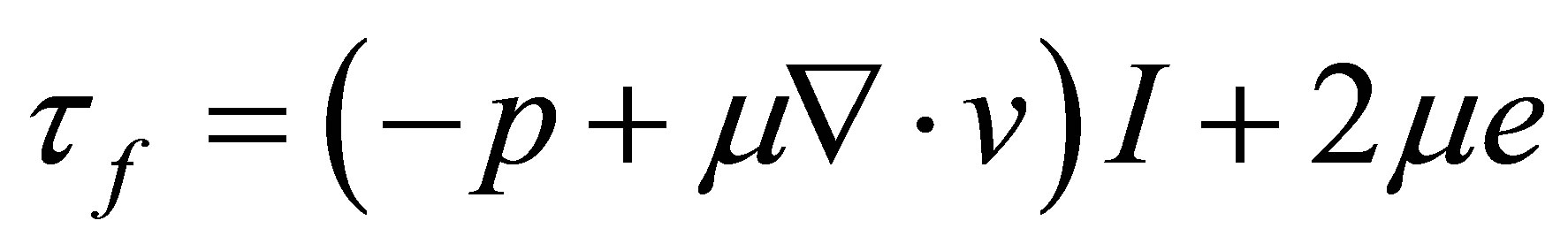 (3)
(3)
where t is time,  is the body force vector,
is the body force vector, 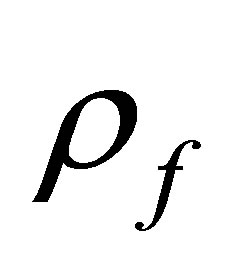 is the density of fluid, v is the fluid velocity vector,
is the density of fluid, v is the fluid velocity vector, 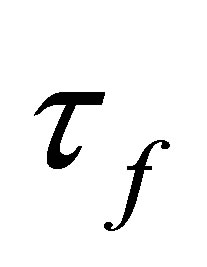 is the shear stress tensor, p is the fluid pressure, μ is the dynamic viscosity, e is velocity stress tensor
is the shear stress tensor, p is the fluid pressure, μ is the dynamic viscosity, e is velocity stress tensor
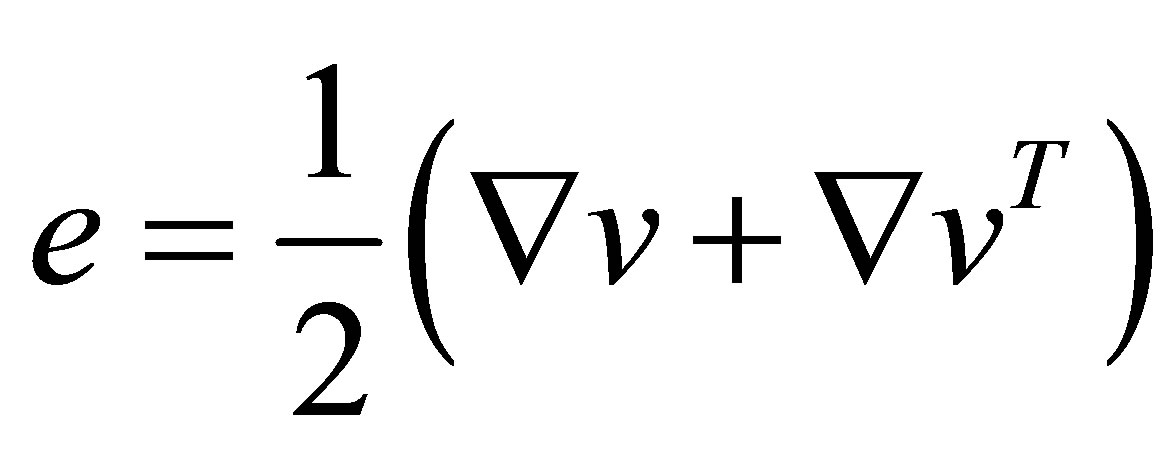 (4)
(4)
The governing equation for the solid domain is derived from Newton’s second law
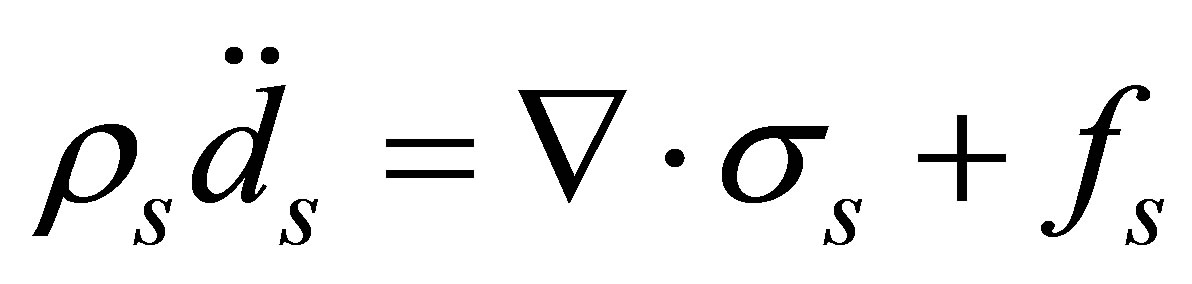 (5)
(5)
where  is solid density,
is solid density, 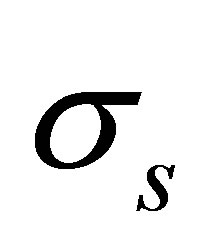 is the Cauchy stress tensor,
is the Cauchy stress tensor, 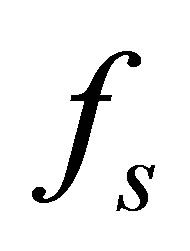 is the body force vector,
is the body force vector,  is a solid domain local acceleration vector.
is a solid domain local acceleration vector.
The variable such as stress , displacement d, heat flow q, temperature T of fluid-structure interaction interface should satisfy the following four equations
, displacement d, heat flow q, temperature T of fluid-structure interaction interface should satisfy the following four equations
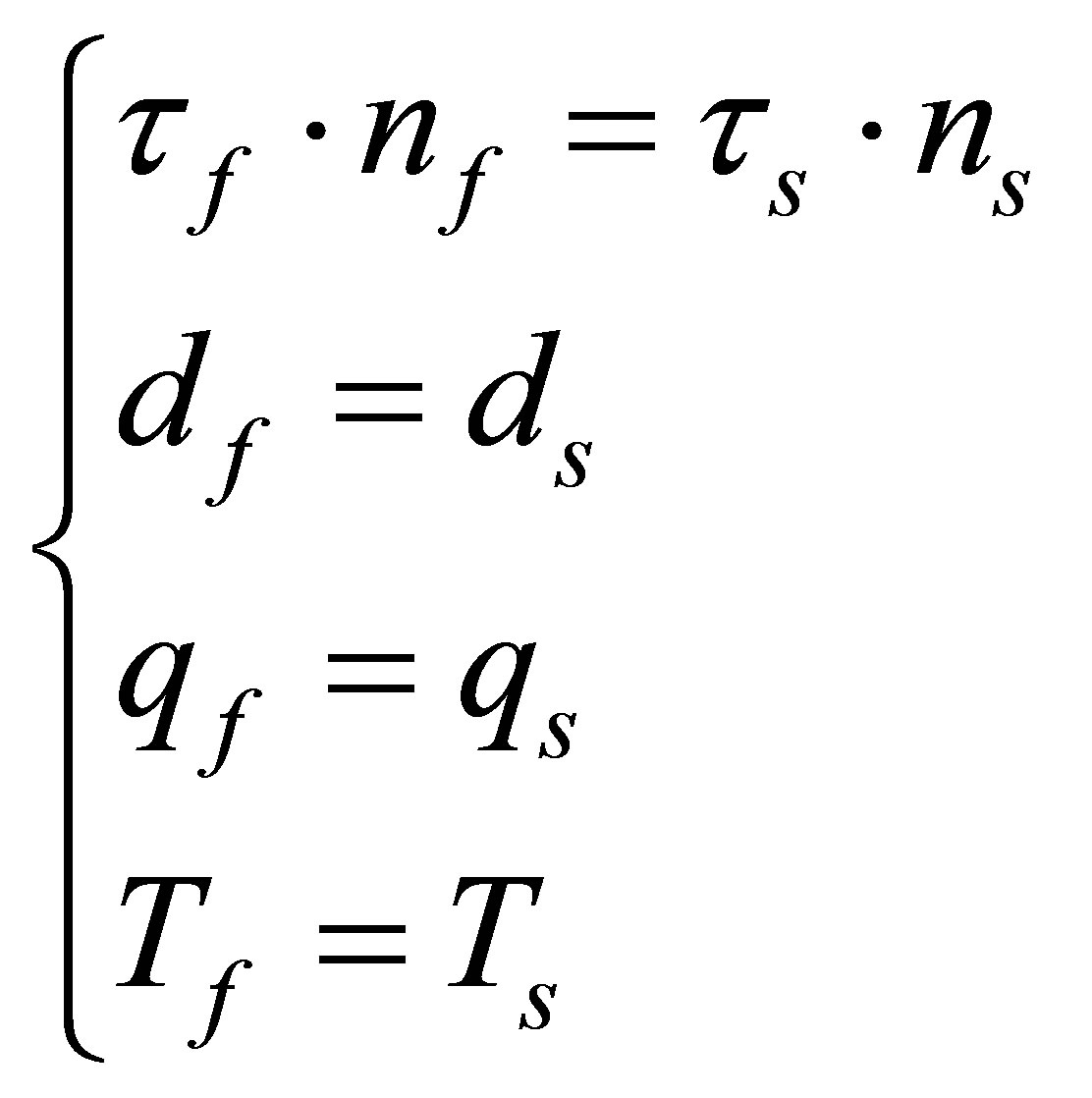 (6)
(6)
2.2. Calculation Model
In the real situation, the rectangular cell culture chamber was length 200 μm, width 100 μm, height 50 μm and the cell diameter was 6 μm. In order to improve the calculation accuracy, 1000 times increased rectangular cell culture chamber was adopted based on the similarity princeple. Then the calculating chamber was length 200 mm, width 100 mm, height 50 mm and the cell diameter was 6 mm. The left was set for fluid inlet, right for outlet. The symmetric boundary conditions were taken in the width direction. In the flow chamber, the distance of leukocyte from the bottom and the inlet was 8.3 mm and 50 mm (Figure 1). In the homogeneous incompressible fluid flow, the acceleration of gravity in the physical model was 9.8 m/s2. The modulus of elasticity and Poisson’s ratio of the leukocyte were 10,000 Pa and 0.3. Other parameters estimation in the models was listed in Table 1.
2.3. Method
The dynamic movement of leukocyte was studied through numerical simulation of fluid-structure interacttion method with FLUENT and ANSYS. The implicit solution model was used and the flow field was based on pressure. Speed inlet flow boundary conditions for the inlet and the free export for the outlet. The Reynolds number was 1.9 so that the flow was laminar. The reference pressure was set to standard atmospheric pressure. The calculation adopted SIMPLEC algorithm and second-order upwind scheme. FLUENT calculated the steady state first. Movement and deformation unsteady calculations followed the steady-state calculations.
Data transferred between FLUENT and ANSYS though the UDF (User Defined Function) procedures on fluid-solid nonlinear coupled interface. At each time step, force and moment of leukocyte in the fluid was calculated first. According to the force and moment calculated in FLUENT, the movement was analyzed by UDF motion analysis program. Then analyzed the deformation based on its force by ANSYS. Leukocyte’s deformation will return to FLUENT and continue the movement calculation, so repeated iterations.
In order to verify the accuracy of the model and method, the blood was changed to air. The ball fell free with an initial velocity of 6.67e−3m/s in x-direction. Since the force on y-direction was too small compared with other directions, we ignored the result of y direction
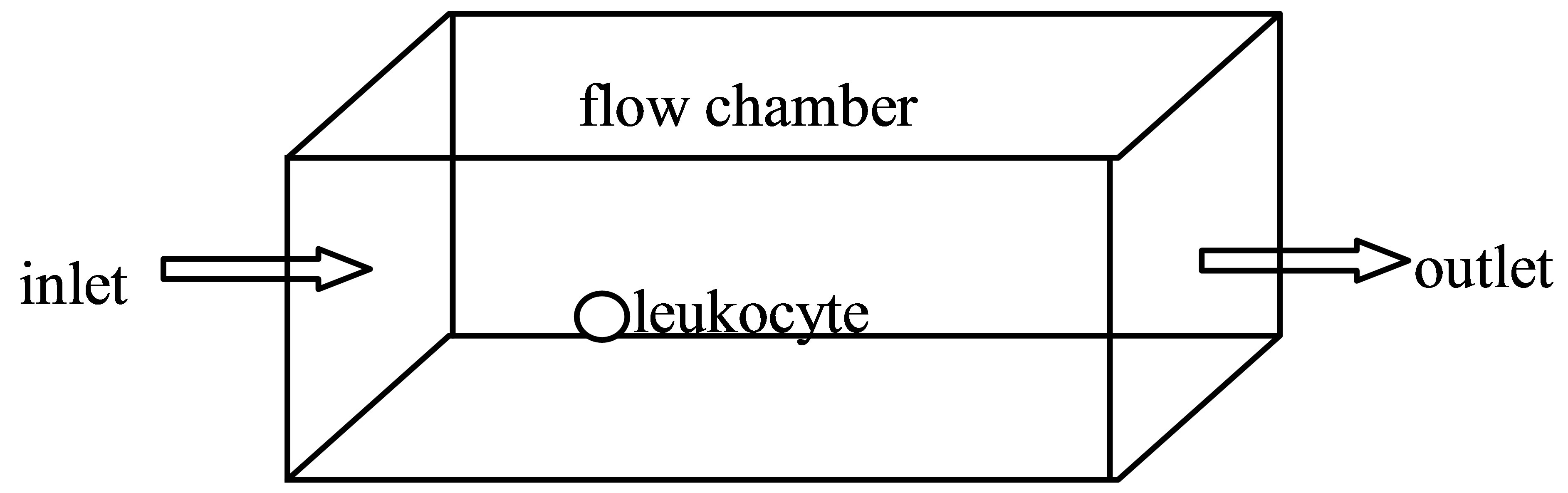
Figure 1. Schematic diagram of a flow chamber with a single leukocyte.
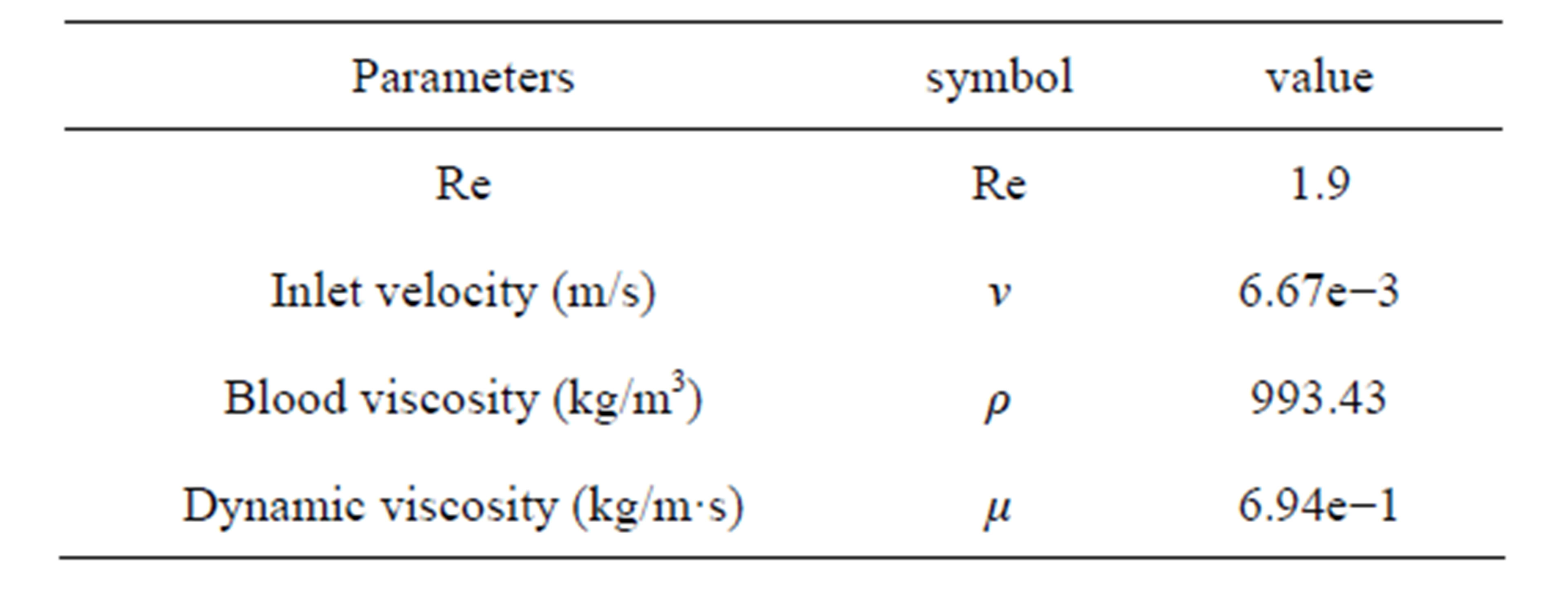
Table 1. Parameters estimation in the models.
and considered displacement and velocity in x-direction and z-direction. The maximum error between calculated values and theoretical values occurred in displacement, which was 1.22% and within the acceptable range. Therefore, the model and method can be used.
3. Results
3.1. Movement of Leukocyte
Time step 5e−4s, 6e−4s and 7e−4s conditions were adopted for calculation. In Figure 2, we can clearly saw the leukocyte bounce trajectory. Figure 2(a) was the increase of x-direction movement. It showed that leukocyte was always moves forward in the direction of blood flow. The x-displacement had a sudden change at every jumping time. After 1.25 second of movement, the leukocyte moved a distance of 3.39e−3m (5e–4 s), 4.02e− 3m (6e−4s) and 5.60e−3 m (7e−4s), with the maximum difference of 2.21e−3m, 1.1% of the total chamber length. The greater the time step, the farther the leukocyte moved in x direction.
Leukocyte moved forward in y-direction at first, followed with moving to the negative y-direction after its first jump. The y-displacement was one order of magnitude less than the other two directions. The results of three kinds of time step calculation were quite different. After 1.25 second of movement, the leukocyte moved a distance of 2.05e−5m (5e−4s), −3.91e−4m (6e−4s) and −1.88e−3 m (7e−4s). The result of time step 7e−4s was almost ten times more than time step 5e−4s and 6e−4s.
Different time steps had little effect in the process of dropping, but the leukocyte bounce time and height differs. Leukocyte dropped from the initial position to the bottom of flow chamber under the influence of gravity where the distance from the initial position to the blood vessel wall is 5.3e−3m. Z-direction movement was more regular than x-direction and y-direction. Leukocyte bounced at position 4.36e−4m instead of landing on the blood vessel wall, with jumping height of 1.69e−3m (5e− 4s). After that, leukocyte began to decline to the near vascular wall and then bounce again periodically. The results of other time step were similarity. In 1.25 second of movement, leukocyte bounced six times for time step 5e−4s, five times for time step 6e−4s and te−4s. The time and distance from bottom while leukocyte jumping were shown in Table 2. The average value and variance of leukocyte bounce cycle was shown in Table 3. Clearly, the Jumping cycle time of time step 6e−4s was the biggest and most stable. However, the height in jumping of time step 7e−4s was becoming bigger and bigger with the increase in number of hitting. Table 4 showed the leukocyte jump height in each cycle.
Figure 3 showed z-velocity of a single leukocyte due to gravity in the flow chamber. The velocity graph dem-
 (a)
(a)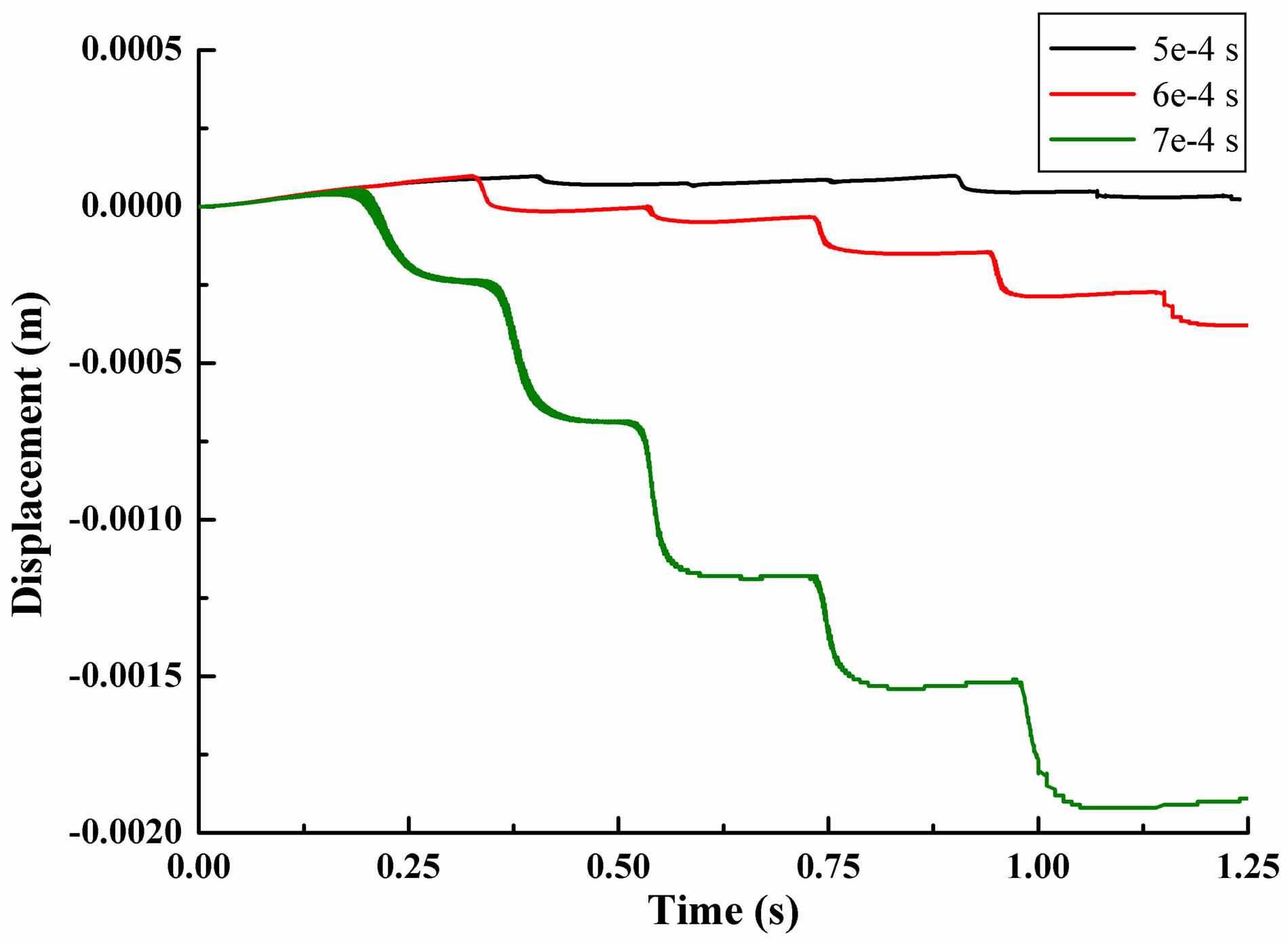 (b)
(b) (c)
(c)
Figure 2. Displacement of a single leukocyte due to gravity in flow chamber. (a) Displacement in x-direction; (b) Displacement in y-direction; (c) Displacement in z-direction.
onstrated oscillatory changes when leukocyte jumping and value increased first and then decreased. Amplitude was uniform when time step was 5e−4s and 6e−4s and increased when time step was 7e−4s. The maximum and
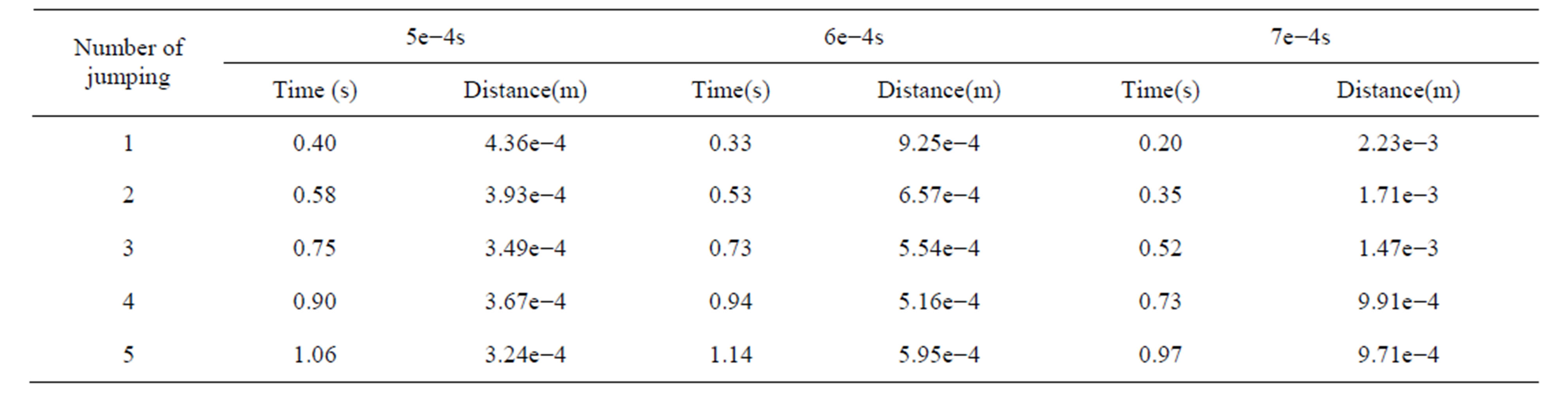
Table 2. Time and distance from bottom while leukocyte jumping.
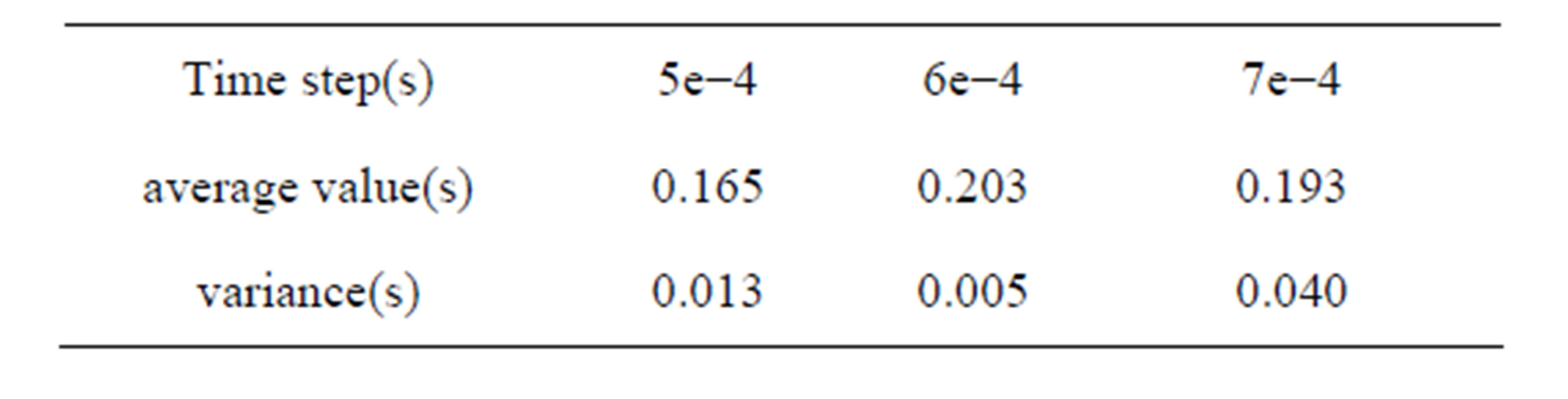
Table 3. Average value and variance of leukocyte bounce cycle.

Table 4. Leukocyte jump height.
the minimum velocity in z-direction were shown in Table 5. The time when velocity reached maximum was corresponding with the jumping time.
Graphical display of local enlargement was shown in Figure 3. Oscillate occurred in different times since difference beating time. The fastest growth and reduce rate was the velocity of time step 5e−4s, followed by time step 6e−4s and the last one was time step 7e−4s. The forces acting on the leukocyte were changed correspondingly.
3.2. Rolling of Leukocyte
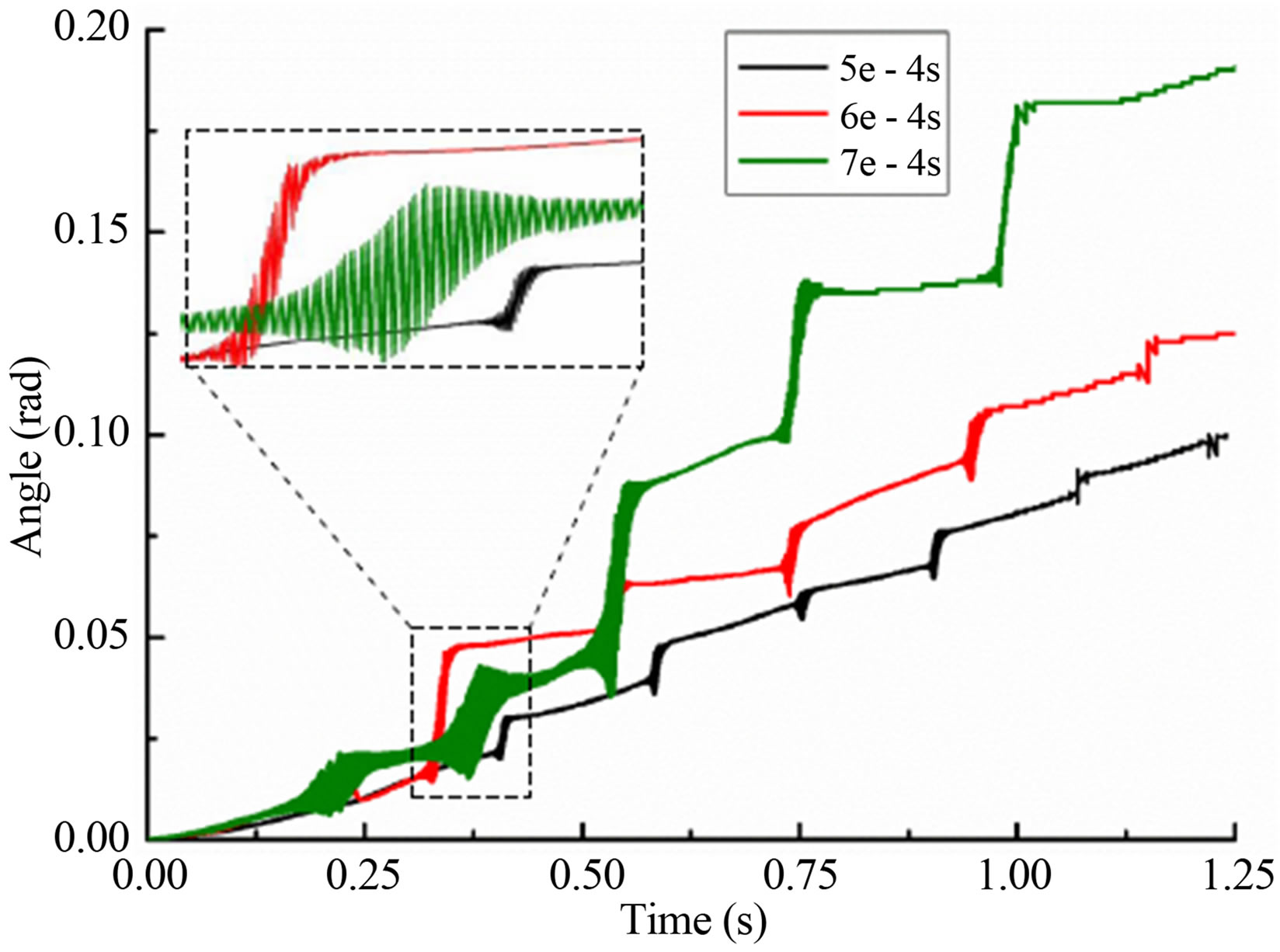
Figure 4 showed the rotation angle of a single leukocyte due to gravity in flow chamber. It was in accordance with the displacement in every jump cycle. With the increasing of time step, leukocyte angle in x direction was becoming larger and always in the positive direction. After 1.25 second, leukocyte rotated 0.099rad (5e−4s), 0.126rad (6e−4s) and 0.191rad (7e−4s). It was the first oscillation for time step 5e-4s in the graphical display of local enlargement. Oscillation time was short, only 0.02 second, while the angle of time step 6e−4s complete oscillations in 0.03 second. In contrast, changes of time step 7e−4s changed more slowly and smoothly.

Figure 3. Z-velocity of a single leukocyte due to gravity in flow chamber.
3.3. Adhesion of Leukocyte
The dynamics of motion of a single leukocyte due to gravity in flow chamber with fixed time step 5e−5s was shown in Figure 5. The initial position of leukocyte movement was seen as zero point in all three directions. Leukocyte jumped at 0.537 second with a distance of 4.7e−5m from the bottom of flow chamber. However, leukocyte dropped to the vessel wall once again and remained stable in the z direction with a distance of 6.7e− 5m from the bottom of flow chamber. Leukocyte moved 5.1e−4m in x-direction in the stable period. Assuming it was pure rolling, the corresponding rotation was 0.17 rad
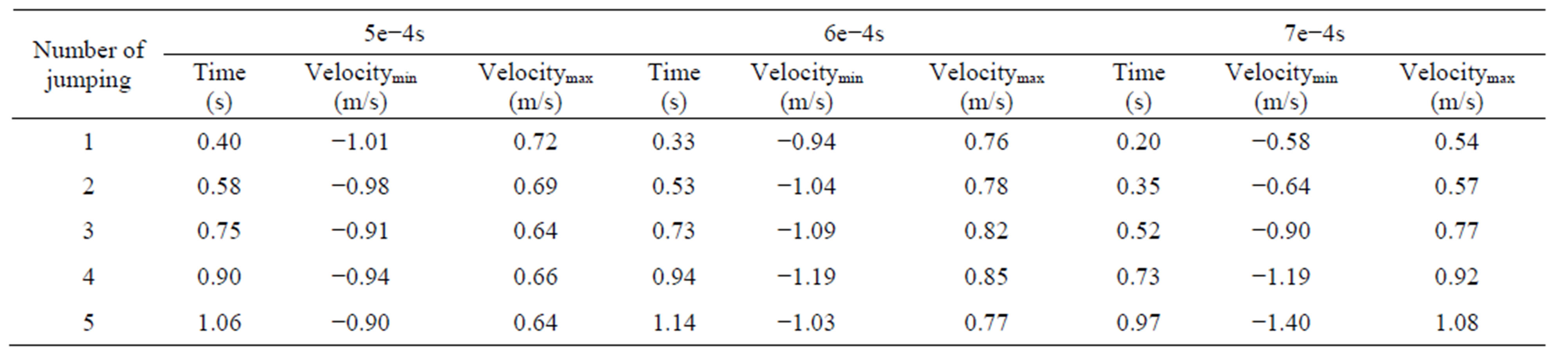
Table 5. The maximum and the minimum velocity in z-direction.
 (a)
(a)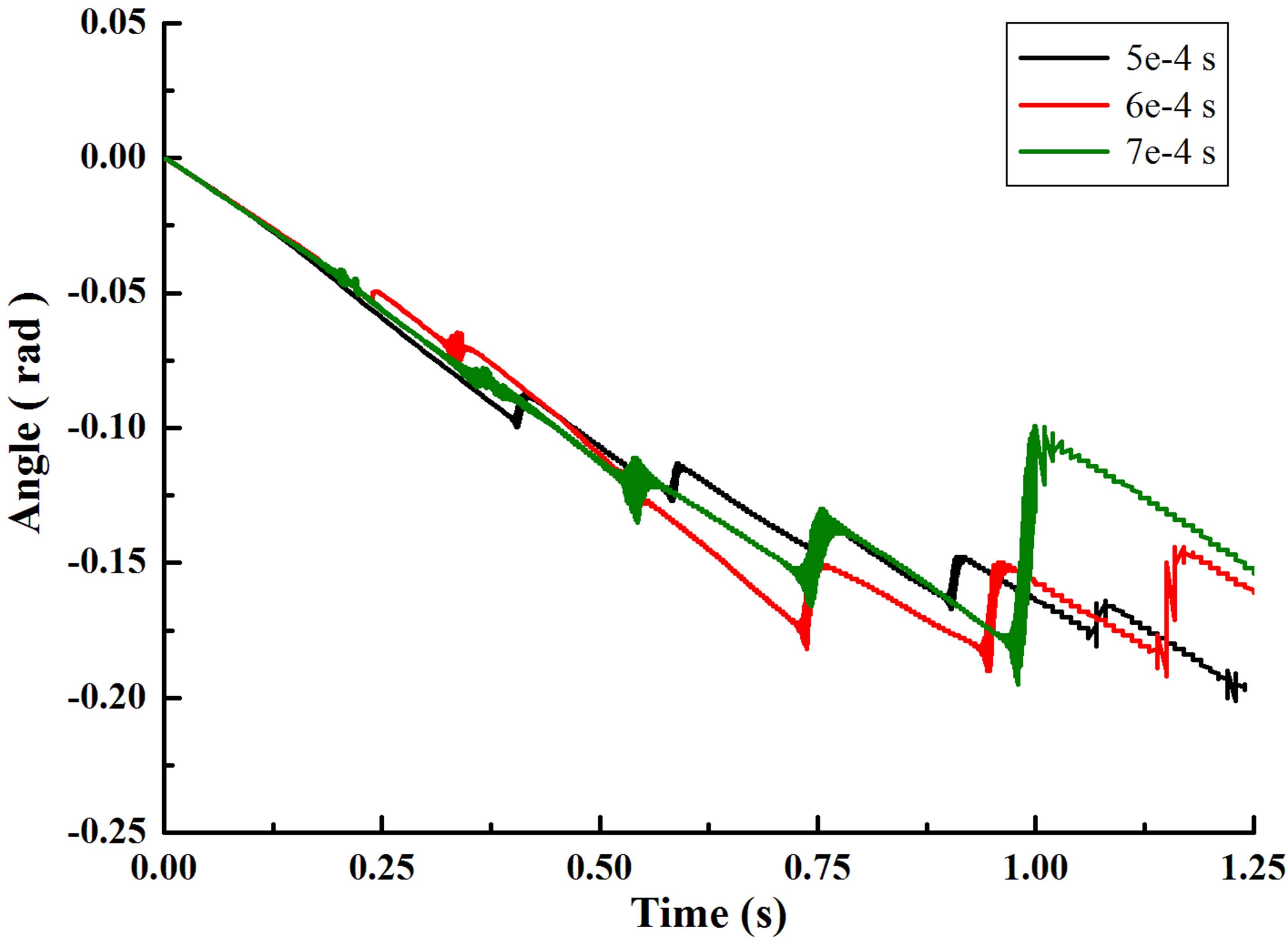 (b)
(b)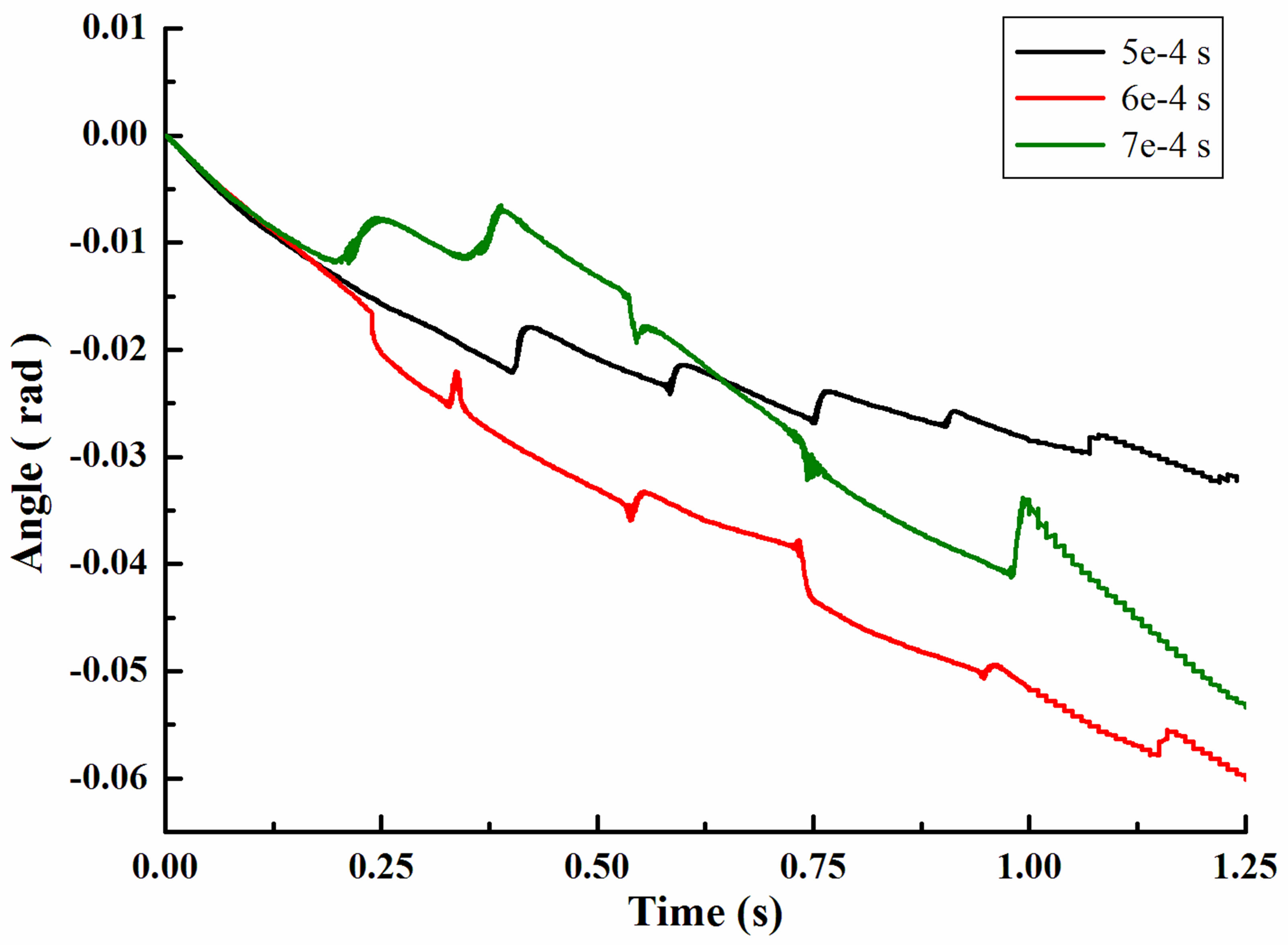 (c)
(c)
Figure 4. Rotation angle of a single leukocyte due to gravity in flow chamber. (a) Angle in x-direction; (b) Angle in ydirection; (c) Angle in z-direction.
 (a)
(a) (b)
(b)
Figure 5. The dynamics of motion of a single leukocyte due to gravity in flow chamber with fixed time step 5e−5s (a) Displacement (b) Angle.
but actually the leukocyte rotated 0.23 rad. Since then the actual angular velocity was faster than pure rolling.
4. Discussion
Leukocyte moved to the bottom of the blood vessels due to gravity. Jumping at a certain distance from the vessel wall appeared with characteristics of cyclical movement instead of directly heating the wall. When leukocyte rises to a certain height, it descends to the bottom and jumps again. The velocity showing oscillatory changes when leukocyte jumping and the forces acting on the leukocyte were also changed correspondingly. The choice of time step of leukocyte had a great influence on the movement of leukocyte. Adhesion in the vicinity of the vessel wall was another significant phenomenon. Since the shear flow was in flow chamber, velocity of leukocyte was greater than the pure rolling.
5. Acknowledgements
Project Supported by Tianjin Research Program of Application Foundation and Advanced Technology 11JCYB JC09700.
REFERENCES
- M. Long, L. Harry, Goldsmith, D. F. J. Tees and C. Zhu, “Probabilistic Modeling of Shear-Induced Formation and Breakage of Doublets Cross-Linked by Receptor-Ligand Bonds,” Biophysical Journal, Vol. 76, No. 2, 1999, pp. 1112-1128. http://dx.doi.org/10.1016/S0006-3495(99)77276-0
- T. Yamaguchi, Y. Yamamoto and H. Liu, “Computational Mechanical Model Studies on the Spontaneous Emergent Morphogenesis of the Cultured Endothelial Cells,” Journal of Biomechanics, Vol. 33, No. 1, 2000, pp. 115-126. http://dx.doi.org/10.1016/S0021-9290(99)00159-1
- K. C. Chang, D. F. Tees and D. A. Hammer, “The State Diagram for Cell Adhesion under Flow: Leukocyte Rolling and Firm Adhesion,” Proceedings of the National Academy of Sciences, Vol. 97, No. 21, 2000, pp. 11262- 11267. http://dx.doi.org/10.1073/pnas.200240897
- M. J. Slattery and C. Dong, “Neutrophils Influence Melanoma Adhesion and Migration under Flow Conditions,” International Journal of Cancer, Vol. 106, No. 5, 2003, pp. 713-722. http://dx.doi.org/10.1002/ijc.11297
- N. A. N’Dri, W. Shyy and R. Tran-Son-Tay, “Computational Modeling of Cell Adhesion and Movement Using a Continuum-Kinetics Approach,” Biophysics Journal, Vol. 84, No. 4, 2003, pp. 2273-2286.
- S. Liang, M. J. Slattery, D. Wagner, S. I. Simon and C. Dong, “Hydrodynamic Shear Rate Regulates MelanomaLeukocyte Aggregation, Melanoma Adhesion to the Endothelium, and Subsequent Extravasation,” Annals of Biomedical Engineering, Vol. 36, No. 4, 2008, pp. 661- 671. http://dx.doi.org/10.1007/s10439-008-9445-8
- A. Squeira, A. M. Artoli, A. S. Silva-Herdade and C. Saldanha, “Leukocytes Dynamics in Microcirculation under Shear-thinning Blood Flow,” Computers and Mathematics with Applications, Vol. 58, No. 5, 2009, pp. 1035-1044. http://dx.doi.org/10.1016/j.camwa.2009.02.003
- X. He, J. Cui, S. Wei and T. Yang, “Lattice Boltzmann Method with Immersed Boundary Method for Simulation RBC Movement in Micro-vessel,” Proceedings of the 8th World Congress on Intelligent Control and Automation, Jinan, 7-9 July 2010, pp. 1953-1958.

