Advances in Pure Mathematics
Vol.04 No.10(2014), Article ID:51068,9 pages
10.4236/apm.2014.410062
Irreducible Representations of Algebraic Group
 in
in
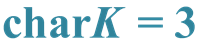
Zhongguo Zhou
College of Science, Hohai University, Nanjing, China
Email: zhgzhou@hhu.edu.cn
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 15 August 2014; revised 12 September 2014; accepted 21 September 2014

ABSTRACT
For each irreducible module
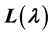 Xi Nanhua defined an element which generated this module. We use this element to construct a certain basis for
Xi Nanhua defined an element which generated this module. We use this element to construct a certain basis for
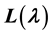 and then compute
and then compute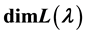 , determine its formal characters in this paper. In order to obtain faster speed we modify the algorithm to compute the irreducible characters.
, determine its formal characters in this paper. In order to obtain faster speed we modify the algorithm to compute the irreducible characters.
Keywords:
Irreducible Character, Semisimple Algebraic Group, Composition Factor

1. Introduction
The determination of all irreducible characters is a big theme in the modular representations of algebraic groups and related finite groups of Lie type. But so far only a little is known concerning it in the case when the characteristic of the base field is less than the Coxeter number.
Gilkey-Seitz gave an algorithm to compute part of characters of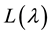 ’s with
’s with
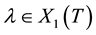 for
for
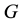 being of type
being of type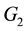 ,
,
 ,
,
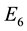 ,
,
 and
and
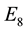 in characteristic 2 and even in larger primes in [1] . Dowd and Sin gave all characters of
in characteristic 2 and even in larger primes in [1] . Dowd and Sin gave all characters of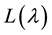 ’s with
’s with
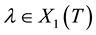 for all groups of rank less than or equal to 4 in characteristic 2 in [2] . They got their results by using the standard Gilkey-Seitz algorithm and computer. L. Scott et al. computes the characters for
for all groups of rank less than or equal to 4 in characteristic 2 in [2] . They got their results by using the standard Gilkey-Seitz algorithm and computer. L. Scott et al. computes the characters for
 when
when



An element



39.1, p. 304] and [[6] , p. 239]. This element could be used in constructing a certain basis for













2. Preliminaries
Let
















be the set of simple roots of

Let






Let


















For
Let














Then the irreducible





For
Then the Steinberg tensor product theorem tells us that
Therefore we can determine all the characters




Recall the strong linkage principle in [12] . We define a strong linkage relation







Let




















Then






gebra over




tively. They are generated by







bra, and




algebra of







particular,








with


Let





As a special case of [[5] , Theorems 6.5 and 6.7], we have
Theorem 1 Assume that




(i) The element


(ii) Let








(iii) As a



By abuse of notations, the images in









3. Characters of Irreducible Modules of
From now on we shall assume that






Now we can obtain our main theorems. Let

for all


form bases of




with

from


Let us mention our computation of



















with

For example, we assume that



It is easy to see that
For






and then we compute the rank of the set


When





Then the Steinberg tensor product theorem tells us that
Therefore, we can determine all characters





Therefore, from the two matrices






We list the matrix





4. Faster Algorithm
In paper [9] [10] , we compute the multiplicity
















For example, suppose to compute



In order to obtain the results the computer must work several days. So we must be careful to avoid error. There are facts to verity the results.
At firstly, we compute the dimension of weight space, then by Sternberg tensor formula and Weyl formula we obtain the decomposition pattern of

1). Symmetry of dimension of weight space. Checking the results the two equations are satisfied:
2). Symmetry of composition factors. From the

3). Positivity of multiplicity of composition factors. All the multiplicity of composition factors we obtained are nonnegative.
4). Linkage principle is hold. If the multiplicity of composition factors

From the representation theory of algebraic groups, all the above results should be hold, so the computational data is compatible with the theory.
5. Main Results
Theorem 2 When
Then





Remark: The table should be read as following. We list the weights in the first collum and write the multiplicity of composition factors as the others elements of tables. For example, from the third row in Table 1, we obtain 00200 0 1 1, this mean
Table 1. The linkage class (00000).
Table 2. The linkage class (00001), (10002).
Table 3. The linkage class (10210), (21021), (02102), (22010), (10010).
Table 4. The linkage class (10012), (10100).
Table 5. The linkage class (12010), (02101), (01012), (20101), (20002).
Table 6. The linkage class (00002), (00010).
Table 7. The linkage class (00100).
Table 8. The linkage class (00122), (01010), (10101), (00022).
According to the symmetry of


So we also have
Acknowledgements
We thank the Editor and the referee for their comments. This work was supported by the Natural Science Fund of Hohai University (2084/409277,2084/407188) and the Fundamental Research Funds for the Central Universities 2009B26914 and 2010B09714. The authors wishes to thank Prof. Ye Jiachen for his helpful advice.
Cite this paper
ZhongguoZhou, (2014) Irreducible Representations of Algebraic Group SL(6,K) in charK =3. Advances in Pure Mathematics,04,535-544. doi: 10.4236/apm.2014.410062
References
- 1. Gilkey, P.B. and Seitz, G.M. (1988) Some Representations of Exceptional Lie Algebras. Geometriae Dedicata, 25, 407-416. http://dx.doi.org/10.1007/BF00191935
- 2. Dowd, M. and Sin, P. (1996) On Representations of Algebraic Groups in Characteristic Two. Communications in Algebra, 24, 2597-2686. http://dx.doi.org/10.1007/BF00191935
- 3. http://pi.math.virginia.edu/~lls2l/research_undergrad.htm
- 4. http://math.rutgers.edu/~asbuch/dynkin/
- 5. Lusztig, G. (1993) Introduction to Quantum Groups. Progress in Mathematics, 110, Birkháuser.
- 6. Xi, N.H. (1996) Irreducible Modules of Quantized Enveloping Algebras at Roots of 1. Publ. RIMS, Kyoto Univ, 32, 235-276. http://dx.doi.org/10.2977/prims/1195162964
- 7. Xu, B.X. and Ye, J.C. (1997) Irreducible Characters of Algebraic Groups in Characteristic Two (I). Algebra Colloquium, 4, 281-290.
- 8. Ye, J.C. and Zhou, Z.G. (2000) Irreducible Characters of Algebraic Groups in Characteristic Two (III). Communications in Algebra, 28, 4227-4247. http://dx.doi.org/10.1080/00927870008827086
- 9. Ye, J.C. and Zhou, Z.G. (2001) Irreducible Characters for Algebraic Groups in Characteristic Three. Communications in Algebra, 29, 201-223. http://dx.doi.org/10.1081/AGB-100000795
- 10. Ye, J.C. and Zhou, Z.G. (2002) Irreducible Characters for Algebraic Groups in characteristic Three (II). Communications in Algebra, 30, 273-306. http://dx.doi.org/10.1081/AGB-120006491
- 11. Jantzen, J.C. (1987) Representations of Algebraic Groups. Academic Press, Orlando.
- 12. Andersen, H.H. (1980) The Strong Linkage Principle. Journal fur die Reine und Angewandte Mathematik, 315, 53-59.



































