ABSTRACT

An hierarchical circularly iterative method is introduced for solving a system of variational circularly inequalities with set of fixed points of strongly quasi-nonexpansive mapping problems in this paper. Under some suitable conditions, strong convergence results for the hierarchical circularly iterative sequence are proved in the setting of Hilbert spaces. Our scheme can be regarded as a more general variant of the algorithm proposed by Maingé.

1. Introduction

For a given nonlinear operator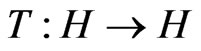, the following classical variational inequality problem is formulated as finding a point such that

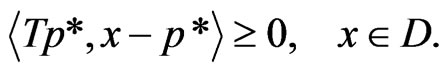
Variational inequalities were initially studied by Stampacchia [1] and ever since have been widely studied, since they cover as diverse disciplines as partial differential equations, optimal control, optimization, mathematical programming, mechanics, and finance. On the other hand, a number of mathematical programs and iterative algorithms have been developed to resolve complex real world problems.

The concept of variational inequalities plays an important role in structural analysis, mechanics and economics. Recently, the hierarchical variational inequalities and hierarchical iterative sequence problems have attached many authors’ attention (see [2-11]).

2. Preliminaries and Lemma

It is well-known that, for any, there exists a unique nearest point in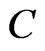, denoted by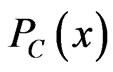, such that

.

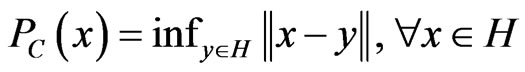Such a mapping from 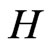onto 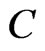is called the metric projection.

Lemma 2.1 (see [12]) The metric projection has the following basic properties:

1) 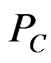is firmly nonexpansive, i.e.,

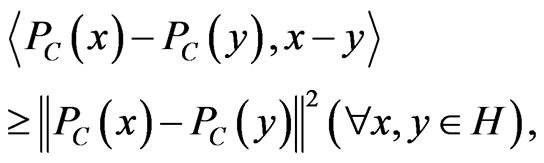
and so is nonexpansive.

2)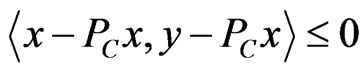, for all 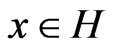and.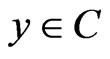

Definition 2.2

1) A mapping 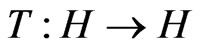is said to be 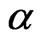-inversestrongly monotone if there exists 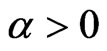such that

.

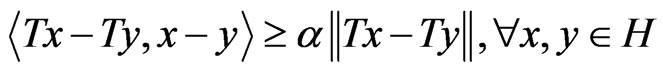2) A mapping 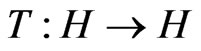is said to be 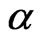-Lipschitzian if

.

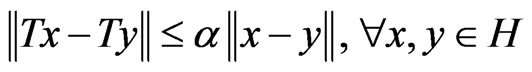3) A mapping 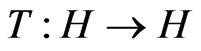is said to be quasinonexpansive if 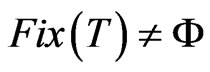and

.

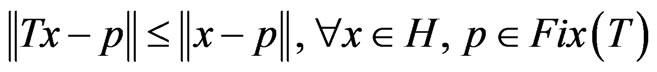4) A mapping 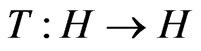is said to be strongly quasi-nonexpansive if 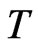is quasi-nonexpansive and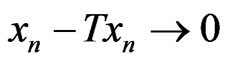, whenever 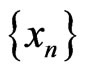is a bounded sequence in H and 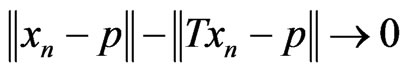for some.

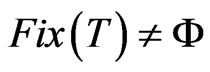5) (see [13]) A mapping is said to be -demicontractive if and

.

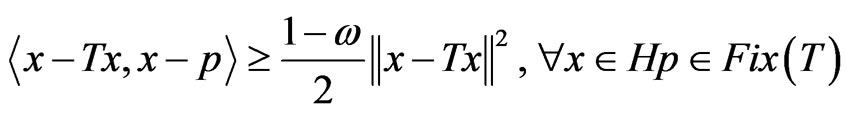Obviously, the above inequality is equivalent to

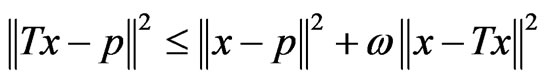and it is clear from the preceding definitions that every quasi-nonexpansive mapping is 0-demicontractive.

Lemma 2.3 (see [14]) For 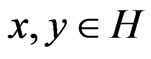and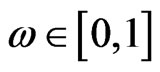, we have the following statements:

a);

b);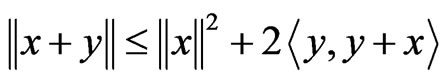

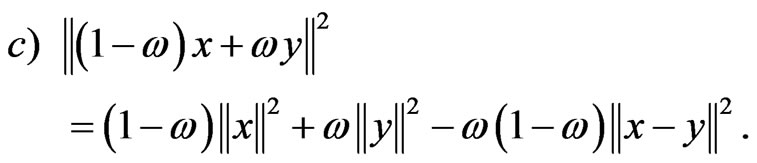
For prove our result, we give the following lemma.

Lemma 2.4 ([11]) Let 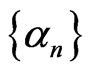be a sequence of real numbers such that there exists a subsequence 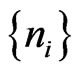of such that 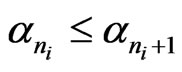for all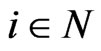. Then there exists a nondecreasing, such that

and the following properties are satisfied for all (sufficiently large) numbers sequence: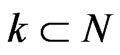

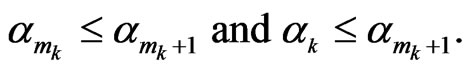
In fact,.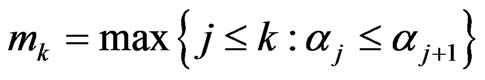

Lemma 2.5 ([11]) Assume that 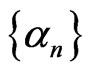is a sequence of nonnegative real numbers such that

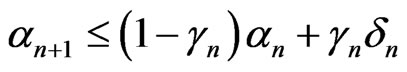where 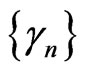is a sequence in 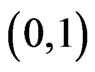and 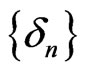is a sequence such that (a)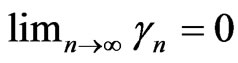, , 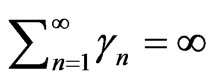(b)

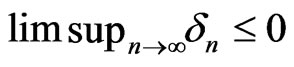. Then.

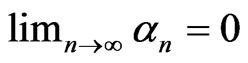Lemma 2.6 ([11]) Let,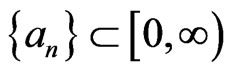

and, such that

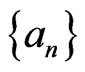• is a bounded sequence;

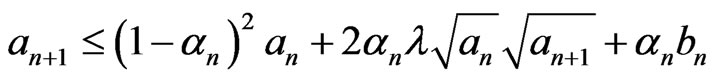• , for all;

• whenever 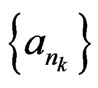is a subsequence of 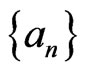satisfying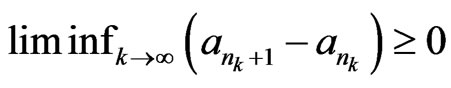, it follows that

;

• ,.

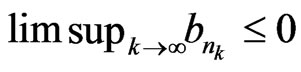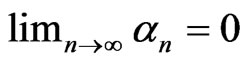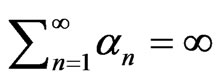Then.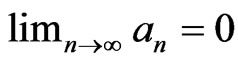

In [11], the existence and uniqueness of solutions of some related hierarchical optimization problems had been discussed.

Inspired by these results in the literature, a circularly iterative method in this paper is introduced for solving a system of variational inequalities with fixed-point set constraints. Under suitable conditions, strong convergence results are proved in the setting of Hilbert spaces. Our scheme can be regarded as a more general variant of the algorithm proposed by Maingé. The results presented in the paper improve and extend the corresponding results in [11] and other.

3. Main Results

First, we discuss the existence and uniqueness of solutions of some related hierarchical optimization problems.

Theorem 3.1 Let 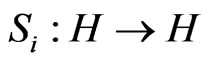be quasi-nonexpansive mappings and 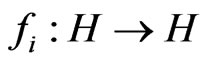be contractions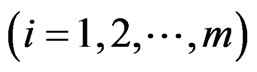. Then there exists a unique element 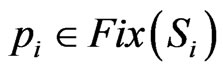such that the following inequalities,

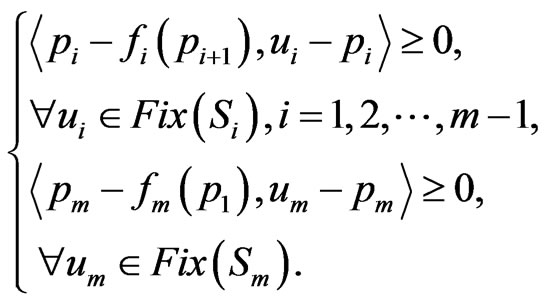(1)

Proof. The proof is a consequence of the well-known Banach’s contraction principle but it is given here for the sake of completeness. It is known that both sets 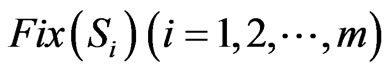are closed and convex, and hence the projections 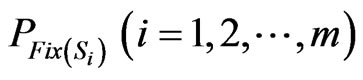are well defined. It is clear that the mapping

is a contraction. Hence, there exists a unique element 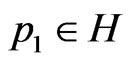such that

.

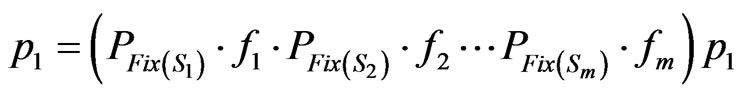Put 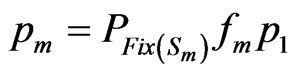and

.

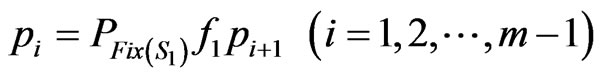Then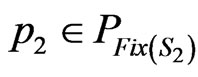, 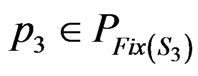and.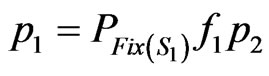

Suppose that there is an element

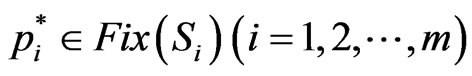such that the following inequalities,

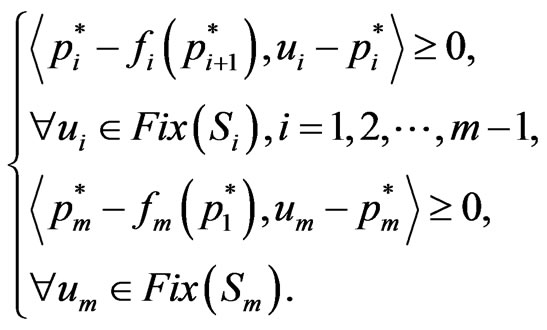
Then and

.

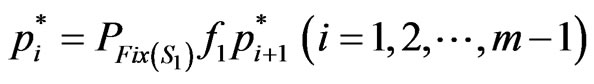Hence,

.

This implies that and hence

.

This completes the proof.

For mappings, suppose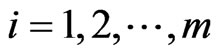we define the iterative sequences 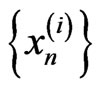by

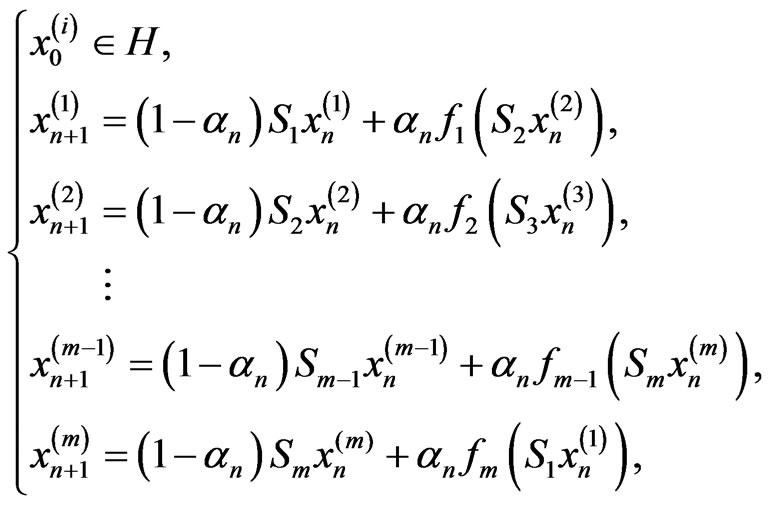(2)

where 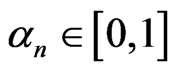satisfy,.

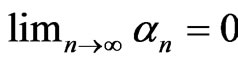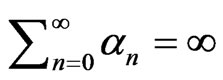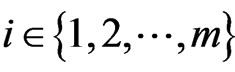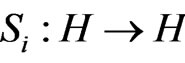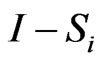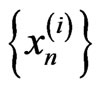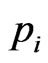Theorem 3.2 For every, let be strongly quasi-nonexpansive mappings such that are demiclosed at zero and let be contractions with the coefficient. Then the iterative sequences by (2) strong converge to, respectively, where is the unique element in 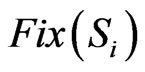verifying (1).

Recall that a mapping 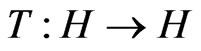is demiclosed at zero iff 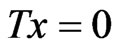whenever 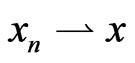and.

We split the proof of Theorem 3.2 into the following lemmas.

Lemma 3.3 The sequences 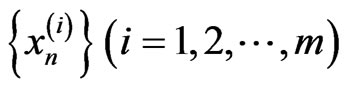are bounded.

Proof. Since 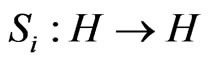be strongly quasi-nonexpansive mappings, 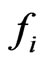be contractions with the coefficient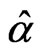. Then we have

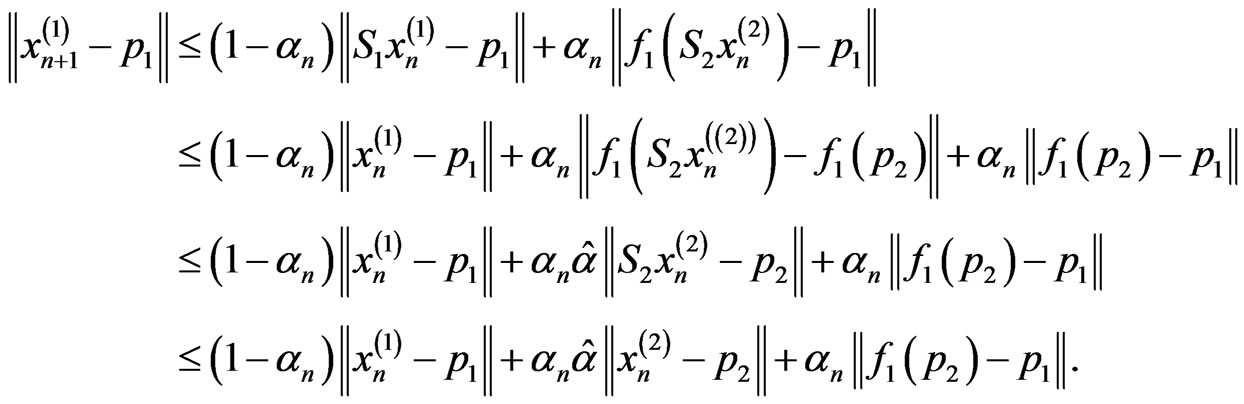
Similarly, we also have

It implies that

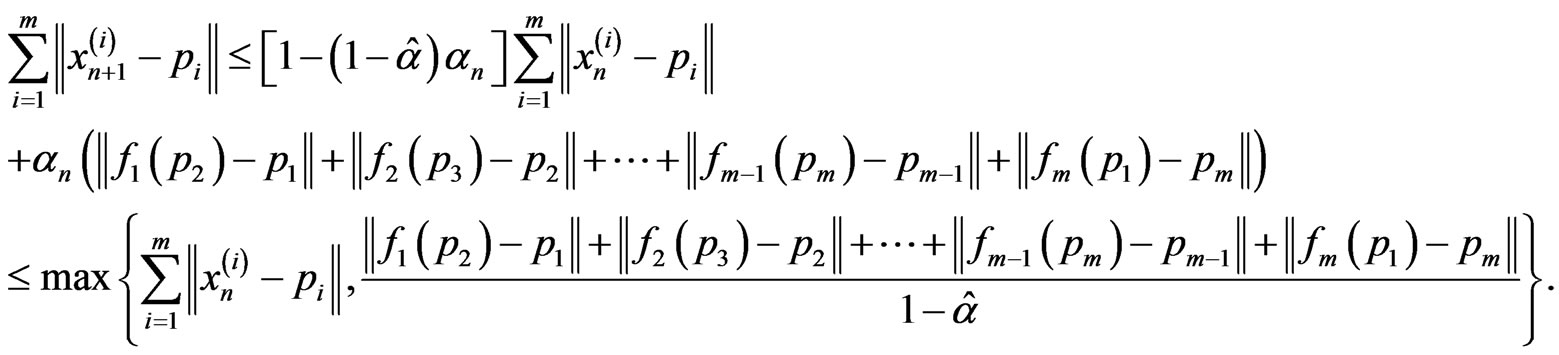
By induction, we have

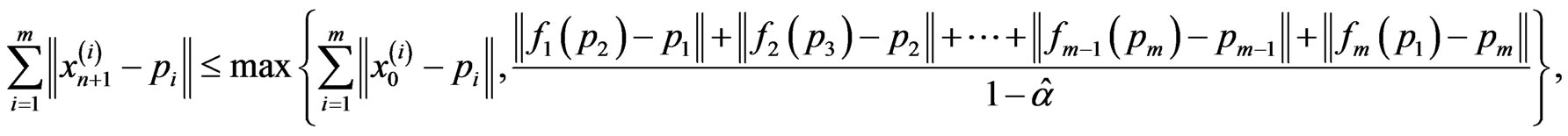
for all. In particular, sequences 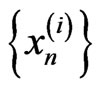are bounded. Consequently, the sequences 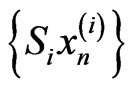are also bounded.

Lemma 3.4 For each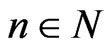, the following inequality holds:

(3)

Proof. Since

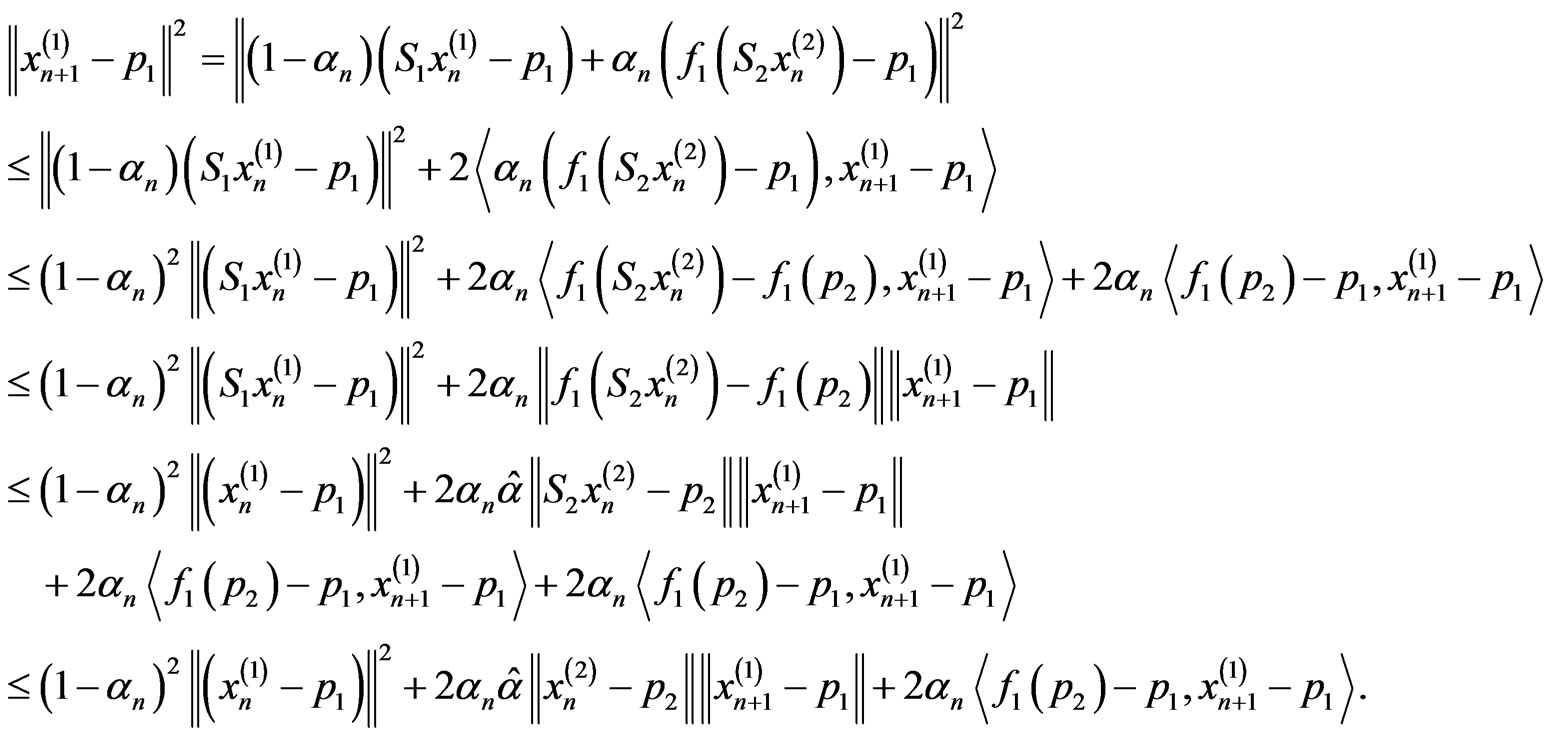
Similarly, we also have

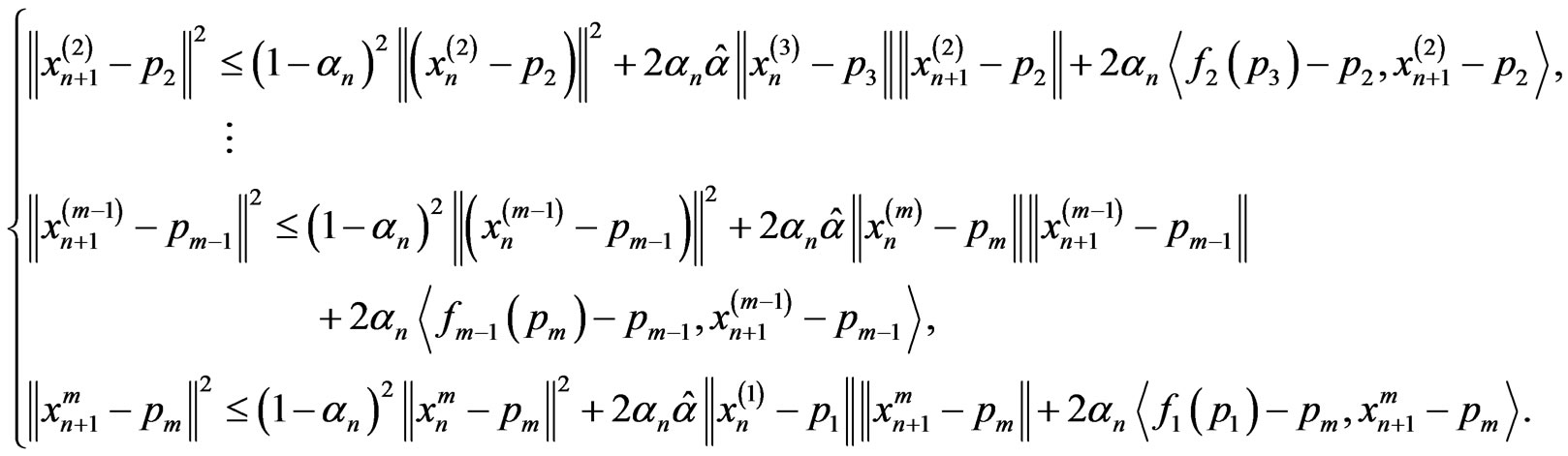
By Lemma 3.3, we give following result,

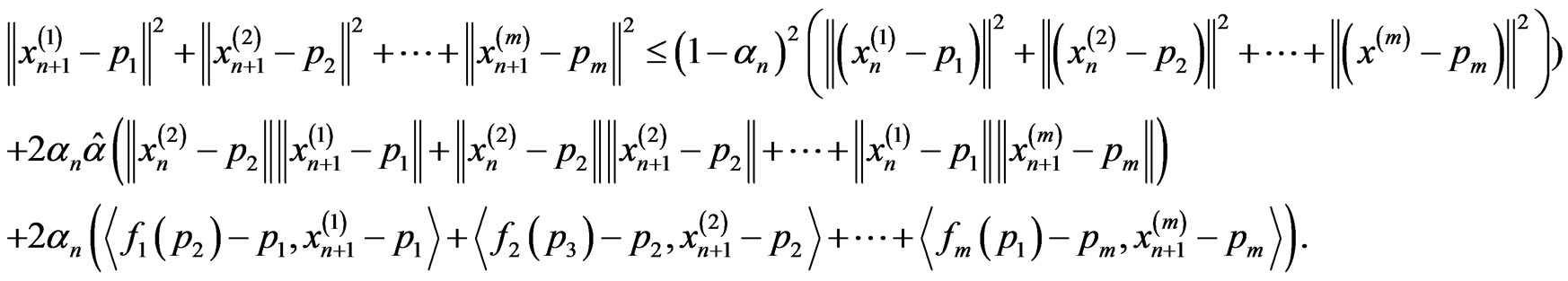(4)

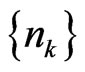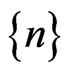Lemma 3.5 If there exists a subsequence of such that

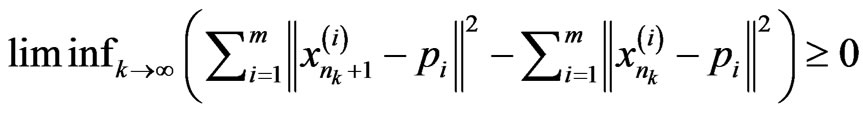then

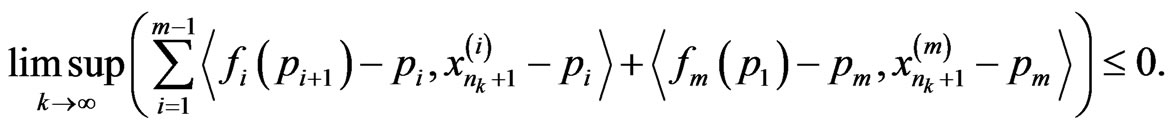(5)

Proof. In fact, we first consider the following assertion:

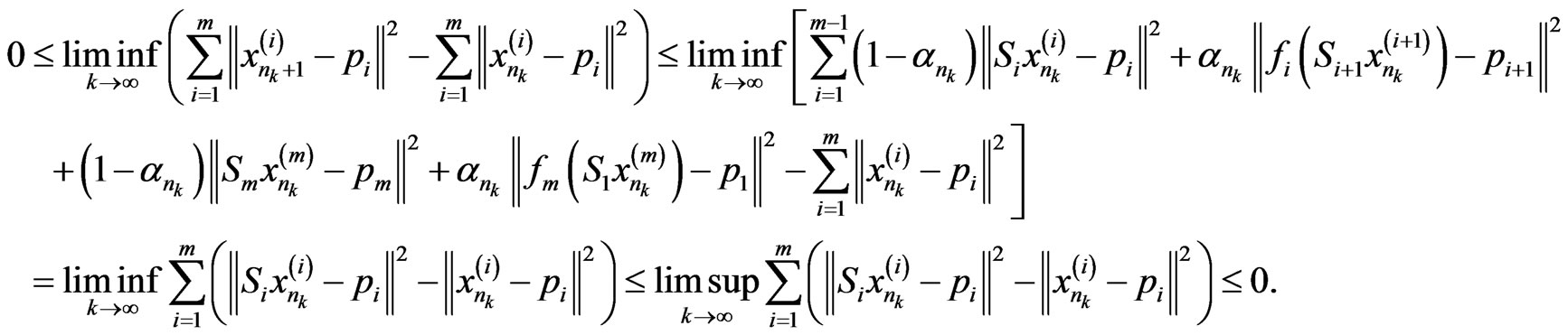
By Lemma 3.3, the sequences

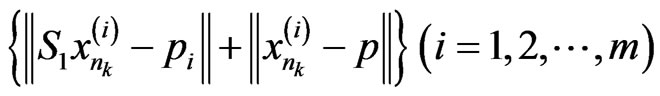
are bounded. So we have

.

Since 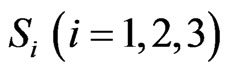are strongly quasi-nonexpansive,

.

by the iteration scheme (1), we have

.

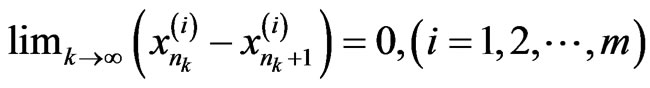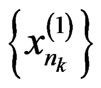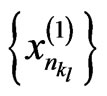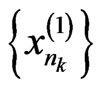It follows from the boundedness of that there exists a subsequence of such that 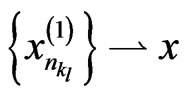and

Since 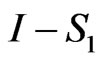is demiclosed at zero, it follows that. It follows from (1), we get

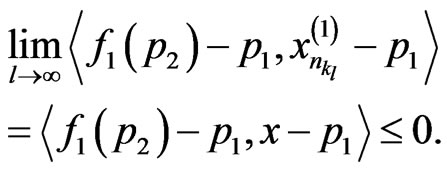
Consequently,

.

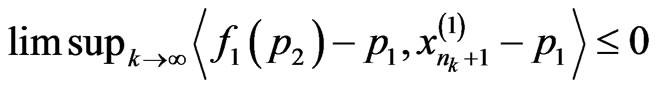By using the same argument, we have

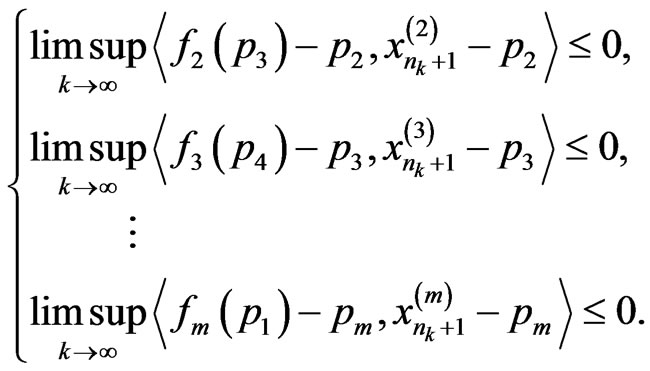
Therefore, we obtain the desired inequality (4).

Next, we prove Theorem 3.2. Denote

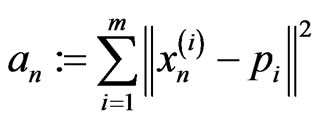
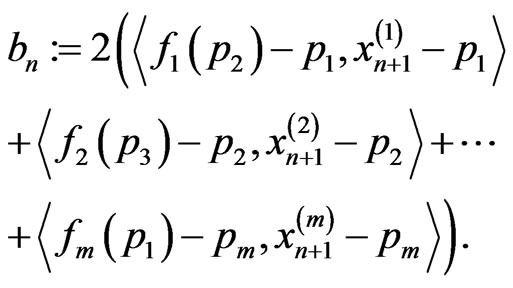
Since

We have the following statements from Lemma (3.3), Lemma(3.4) and Lemma(3.5):

• is a bounded sequence;

• , for all;

• whenever 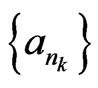is a subsequence of satisfying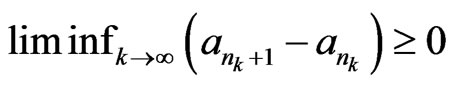, it follows that.

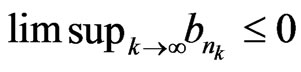Hence, it follows from Lemma 2.6 that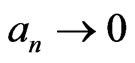, It implies that

.

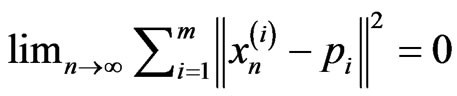This means that

.

The proof of Theorem 3.2 is completed.

REFERENCES