Advances in Pure Mathematics
Vol.3 No.9A(2013), Article ID:40323,6 pages DOI:10.4236/apm.2013.39A1002
Hausdorff Dimension of Multi-Layer Neural Networks
1Department of Applied Mathematics, National Dong Hwa University, Hualien, Taiwan
2Department of Applied Mathematics, Feng Chia University, Taichung, Taiwan
Email: jcban@mail.ndhu.edu.tw, chihhung@mail.fcu.edu.tw
Copyright © 2013 Jung-Chao Ban, Chih-Hung Chang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Jung-Chao Ban, Chih-Hung Chang. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received September 4, 2013; revised October 4, 2013; accepted October 11, 2013
Keywords: Multi-layer neural networks; Hausdorff dimension; sofic shift; output space
ABSTRACT
This elucidation investigates the Hausdorff dimension of the output space of multi-layer neural networks. When the factor map from the covering space of the output space to the output space has a synchronizing word, the Hausdorff dimension of the output space relates to its topological entropy. This clarifies the geometrical structure of the output space in more details.
1. Introduction
The multi-layer neural networks (MNN, [1,2]) have received considerable attention and were successfully applied to many areas such as signal processing, pattern recognition ([3,4]) and combinatorial optimization ([5,6]) in the past few decades. The investigation of mosaic solution is the most essential in MNN models due to the learning algorithm and training processing. In [7-9], the authors proved that the output solutions space 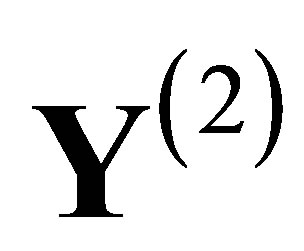 of a 2-layer MNN forms a so-called sofic shift space, which is a factor of a classical subshift of finite type. Thus, MNN model indeed produces abundant output patterns and makes learning algorithm more efficient. A useful quantity to classify the output solution space is the topological entropy
of a 2-layer MNN forms a so-called sofic shift space, which is a factor of a classical subshift of finite type. Thus, MNN model indeed produces abundant output patterns and makes learning algorithm more efficient. A useful quantity to classify the output solution space is the topological entropy  ([10]). We call the output solution space pattern formation if
([10]). We call the output solution space pattern formation if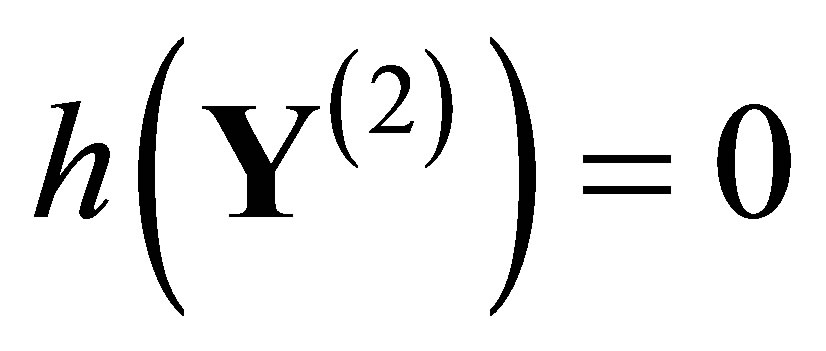 , and call it spatial chaos if
, and call it spatial chaos if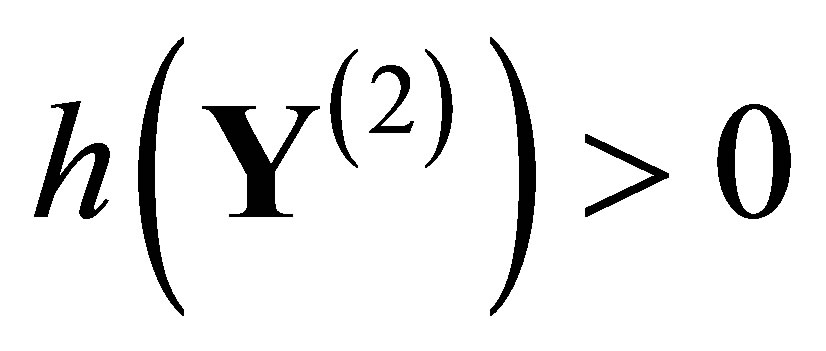 . The
. The 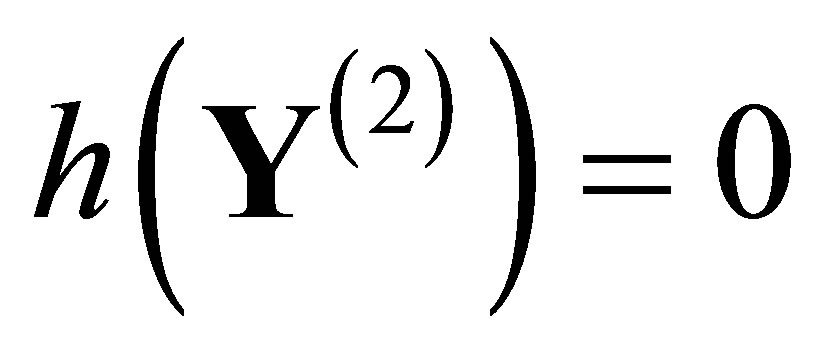 indicates that the output patterns grow subexponentially and exponentially for
indicates that the output patterns grow subexponentially and exponentially for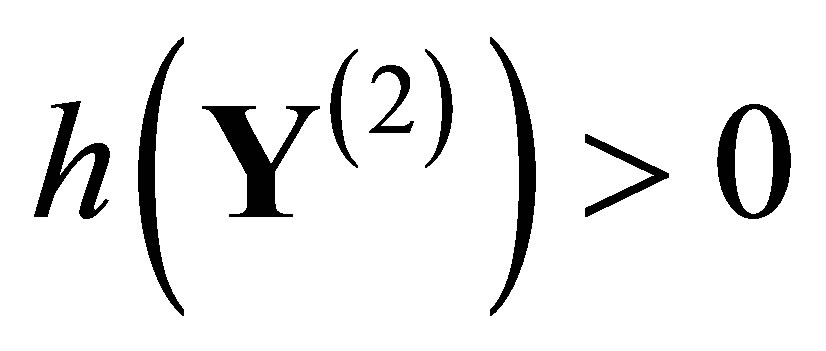 . For positive entropy systems, the explicit value of
. For positive entropy systems, the explicit value of 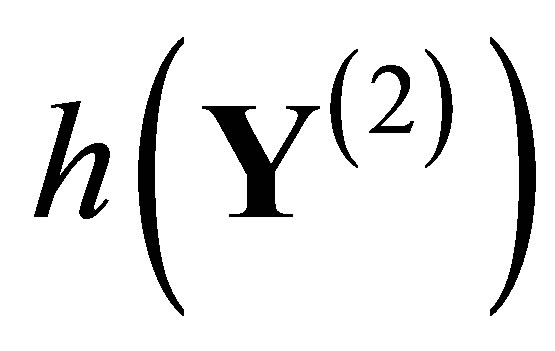 presents how chaotic the system is. In [7], Ban and Chang provided a method to compute explicit values of
presents how chaotic the system is. In [7], Ban and Chang provided a method to compute explicit values of 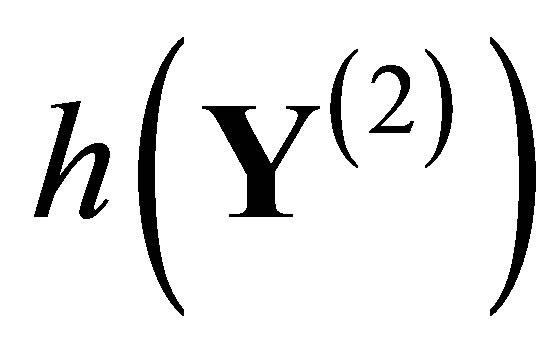 for a
for a 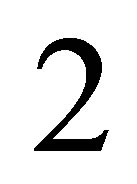 -layer MNN. The method is quite general and it makes the computation of
-layer MNN. The method is quite general and it makes the computation of  possible for arbitrary
possible for arbitrary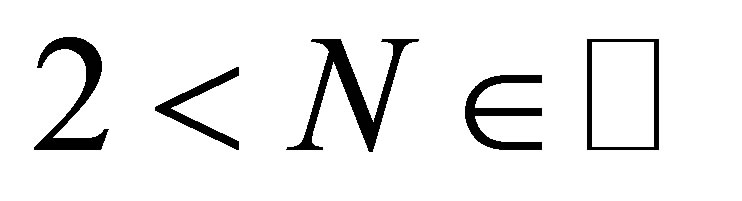 , i.e.,
, i.e., 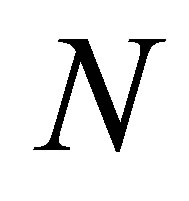 -layer MNN.
-layer MNN.
From the dynamical system (DS) point of view, the topological entropy reveals the complexity of the global patterns. However, it provides less information of the inner structure of a given DS, e.g., self-similarity or recurrent properties. The possible quantity reveals that such properties are the Hausdorff dimension (HD, [11]) since the Hausdorff dimension is an indicator of the geometrical structure. For most DS, the computation of Hausdorff dimension is not an easy task, and the box dimension (BD) is usually computed first to give the upper bound for HD. Due to the relationship of topological entropy and BD ([12]) of a symbolic DS1, the previous work ([7]) for topological entropy gives the upper bound for HD of  -layer MNN. Nature question arises: Given a MNN, how to compute the explicit value for HD? The aim of this paper is to establish the HD formula for
-layer MNN. Nature question arises: Given a MNN, how to compute the explicit value for HD? The aim of this paper is to establish the HD formula for  -layer MNNs. Using the tool of symbolic DS, the HD formula will be established for
-layer MNNs. Using the tool of symbolic DS, the HD formula will be established for 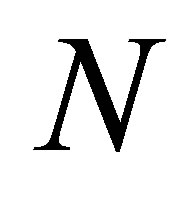 -layer MNNs which possesses a synchronizing word (Theorem 2.4). The result leads us to exploit the inner structure for a
-layer MNNs which possesses a synchronizing word (Theorem 2.4). The result leads us to exploit the inner structure for a 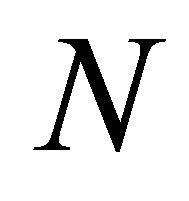 -layer MNN. We believe that further interesting applications of the results presented (or of the generalizations) can be obtained.
-layer MNN. We believe that further interesting applications of the results presented (or of the generalizations) can be obtained.
This paper is organized as follows. Section 2 contains a brief disscussion for the computation of topological entropy in [7]. The main result is stated and proved therein. Section 3 presents an MNN model for which we can compute its HD.
2. Preliminaries and Main Results
A one-dimensional multi-layer neural network (MNN) is realized as
 (1)
(1)
for some ,
, 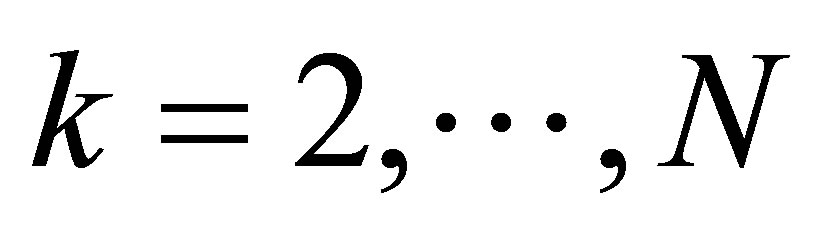 and
and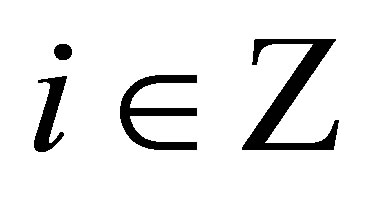 . The finite subset
. The finite subset  indicates the neighborhood, and the piecewise linear map
indicates the neighborhood, and the piecewise linear map
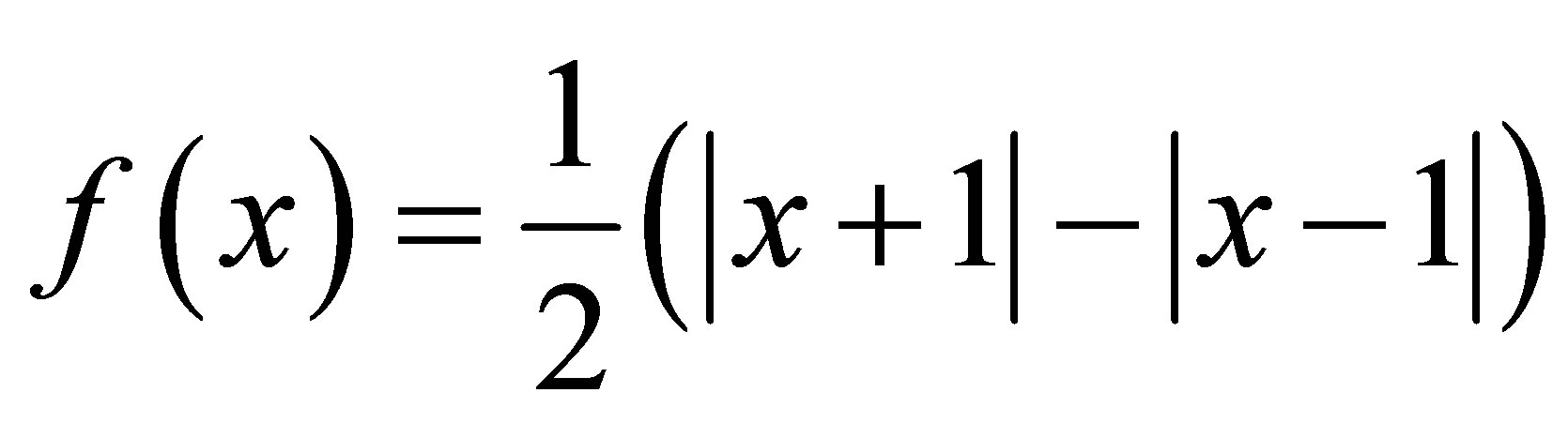
is called the output function. The template 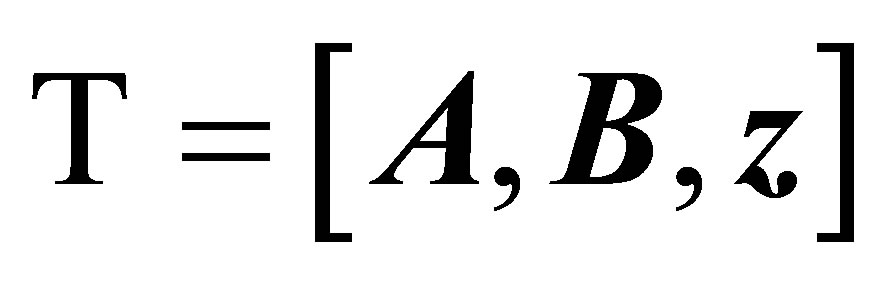 is composed of feedback template
is composed of feedback template  with
with

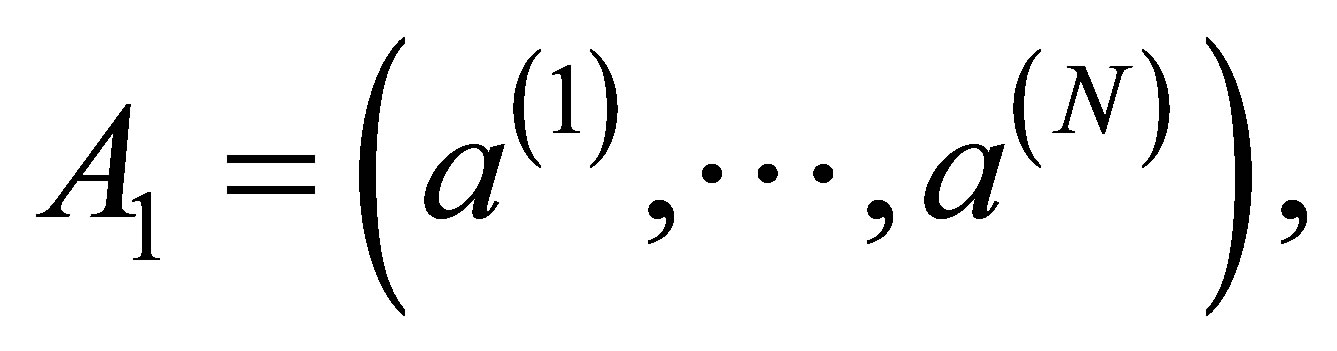 controlling template
controlling template
 and threshold
and threshold
 where
where
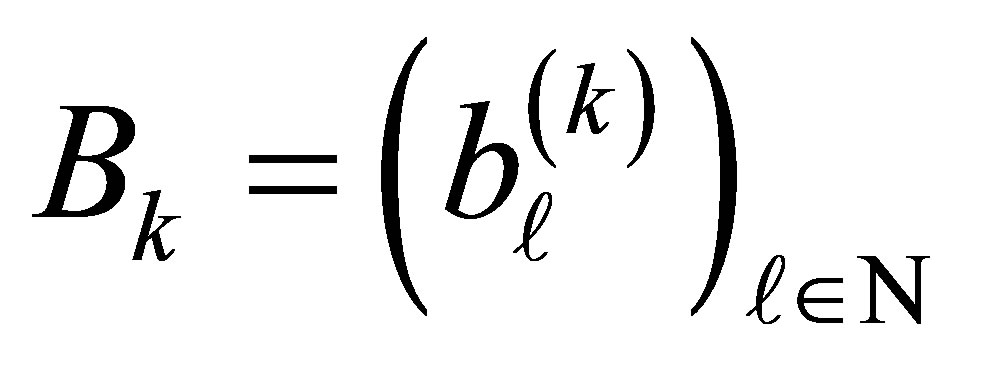 for
for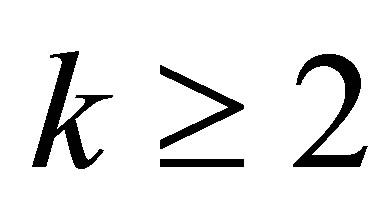 .
.
A solution
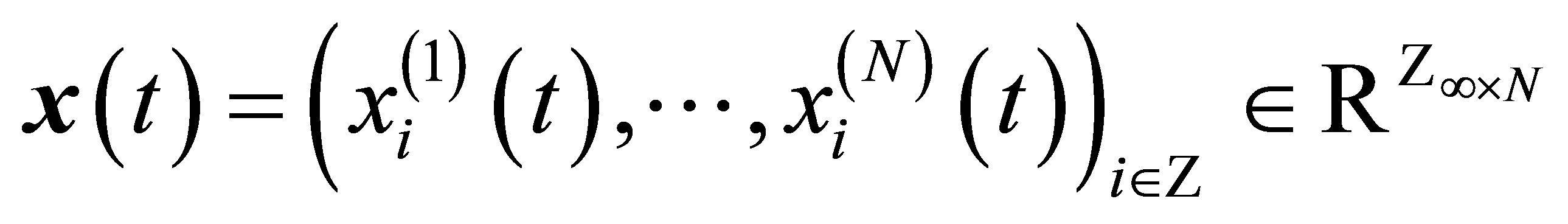
of (1) is called mosaic if

for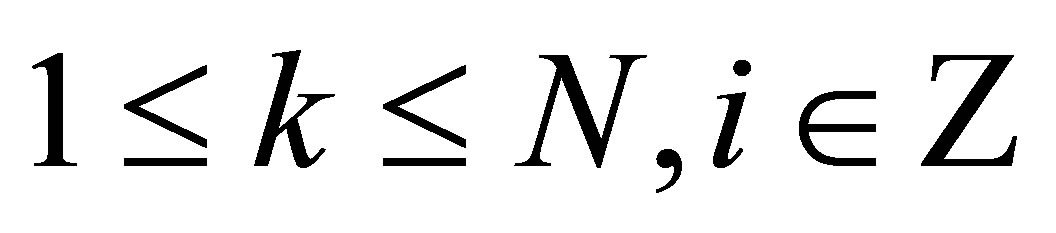 , and
, and 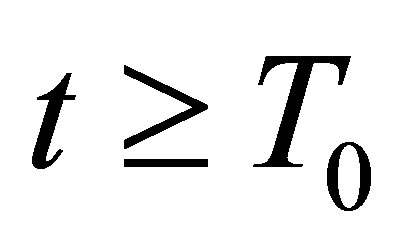 for some
for some .
.
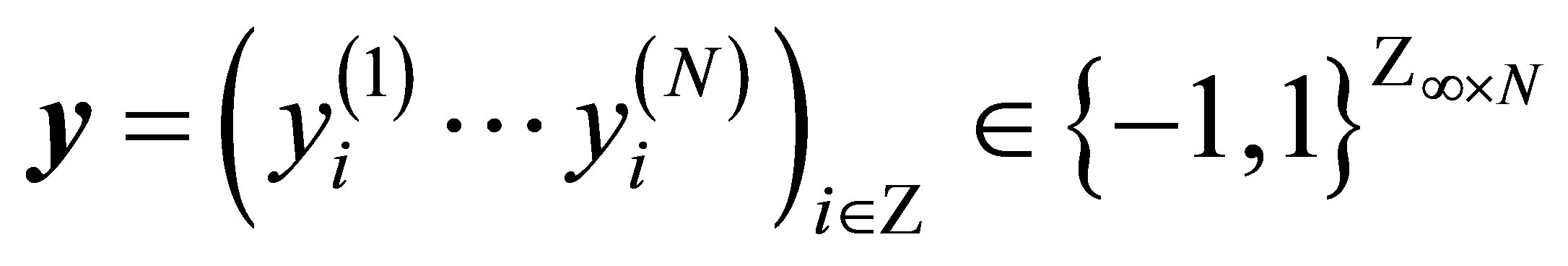
of a mosaic solution is called a mosaic pattern, where
 .
.
The solution space  of (1) stores the patterns
of (1) stores the patterns![]() , and the output space
, and the output space 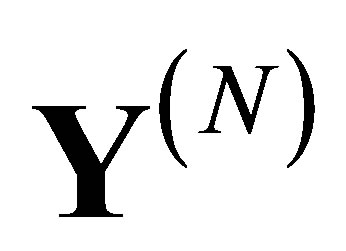 of (1) is the collection of the output patterns; more precisely,
of (1) is the collection of the output patterns; more precisely,
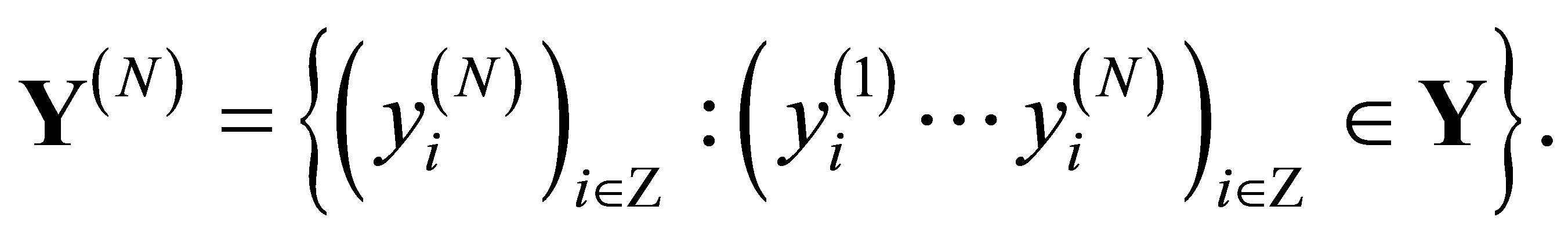
A neighborhood  is called the nearest neighborhood if
is called the nearest neighborhood if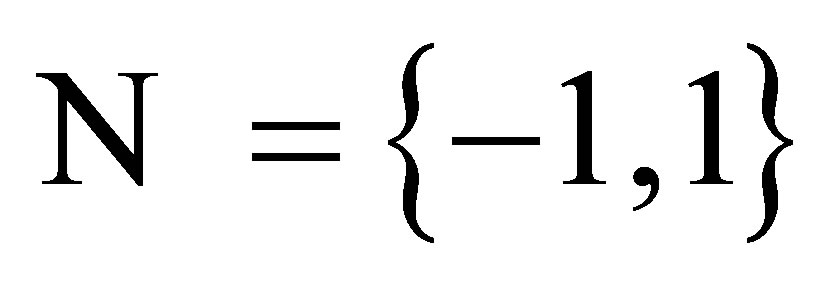 . In [7], the authors showed that
. In [7], the authors showed that  -layer MNNs with nearest neighborhood are essential for the investigation of MNNs. In the rest of this manuscript, we refer MNNs to
-layer MNNs with nearest neighborhood are essential for the investigation of MNNs. In the rest of this manuscript, we refer MNNs to  -layer MNNs with nearest neighborhood unless otherwise stated.
-layer MNNs with nearest neighborhood unless otherwise stated.
2.1. Topological Entropy and Hausdorff Dimension
Since the neighborhood  is finite and is invariant for each
is finite and is invariant for each , the output space is determined by the so-called basic set of admissible local patterns. Replace the pattern -1 and 1 by - and +, respectively; the basic set of admissible local patterns of the first and second layer is a subset of
, the output space is determined by the so-called basic set of admissible local patterns. Replace the pattern -1 and 1 by - and +, respectively; the basic set of admissible local patterns of the first and second layer is a subset of
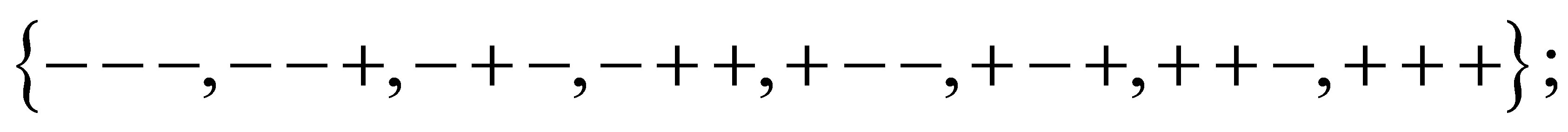 (2)
(2)
and , respectively, where
, respectively, where  denotes
denotes
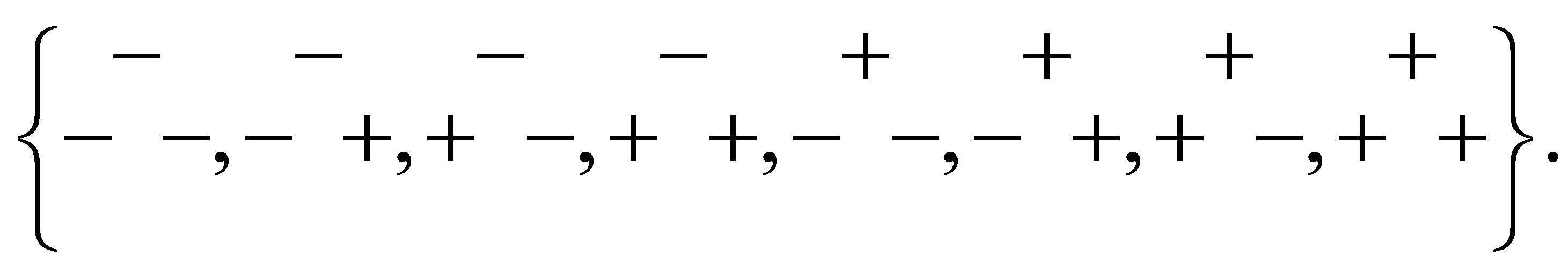 (3)
(3)
To ease the notation, we denote

by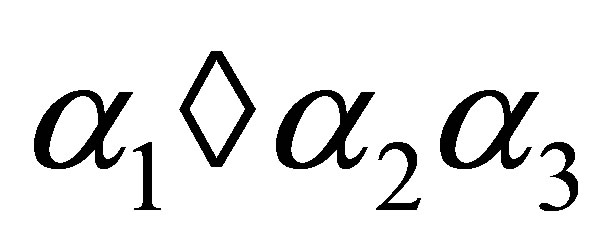 . Given a template
. Given a template![]() , the basic set of admissible local pattern
, the basic set of admissible local pattern

is determined, where  and
and 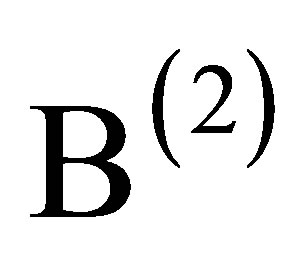 are the basic set of admissible local patterns of the first and second layer, respectively. Let
are the basic set of admissible local patterns of the first and second layer, respectively. Let
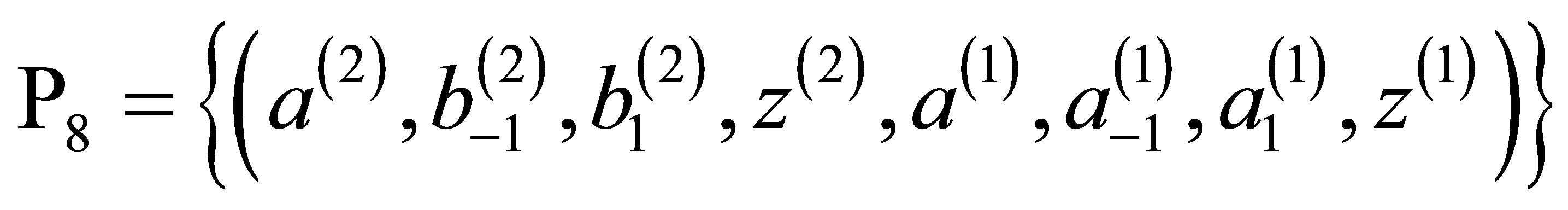
denote the parameter space of (1). Theorem 2.1 asserts that 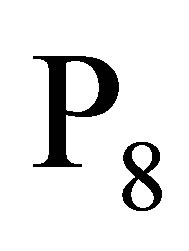 can be partitioned into finitely many subregions so that two templates in the same partition exhibit the same basic set of admissible local patterns.
can be partitioned into finitely many subregions so that two templates in the same partition exhibit the same basic set of admissible local patterns.
Theorem 2.1. (See [7]) There is a positive integer  and unique set of open subregions
and unique set of open subregions 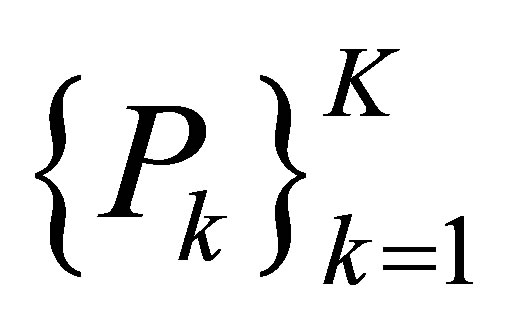 satisfying [(i)]
satisfying [(i)]
1) .
.
2) 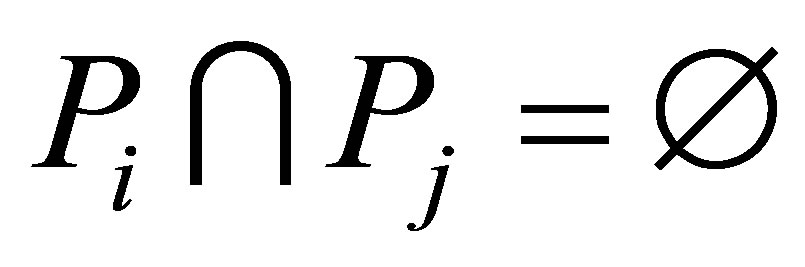 if
if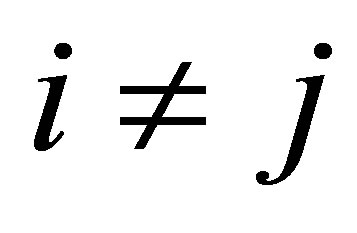 .
.
3) Templates 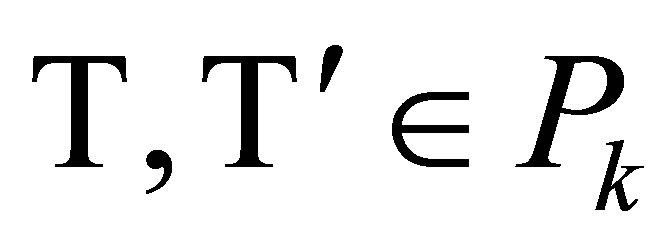 for some
for some 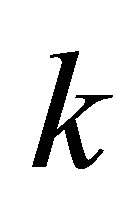 if and only if
if and only if .
.
Since the template of MNNs is spatially invariant, the so-called transition matrix is used to investigate the complexity of MNNs. The transition matrix  is defined by
is defined by
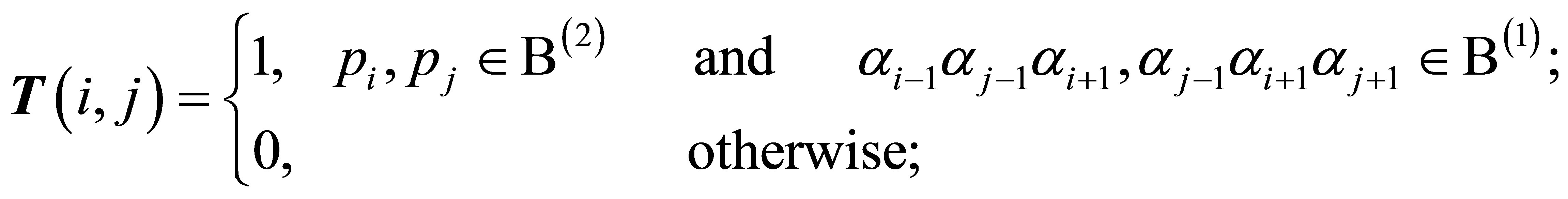 (4)
(4)
herein 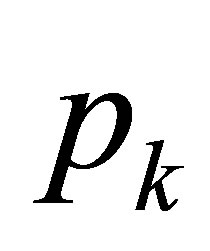 is presented as
is presented as 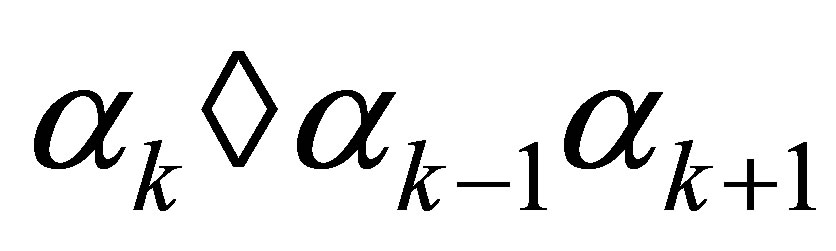 for
for . Furthermore, the transition matrix of the second layer
. Furthermore, the transition matrix of the second layer

is defined by
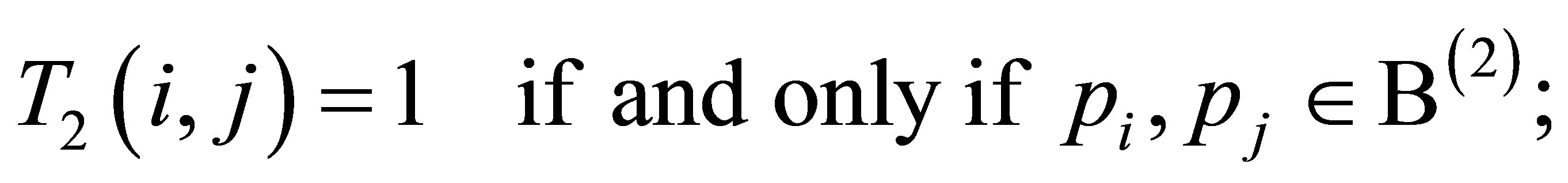 (5)
(5)
the transition matrix of the first layer

is defined by
 (6)
(6)
where

Write
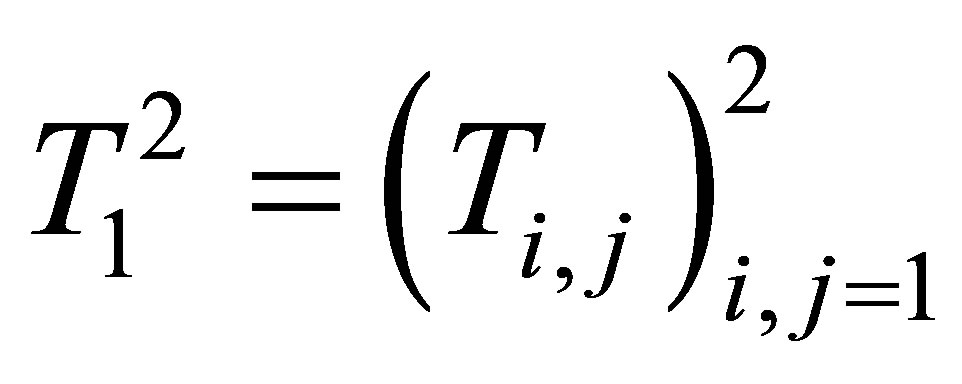
as four smaller 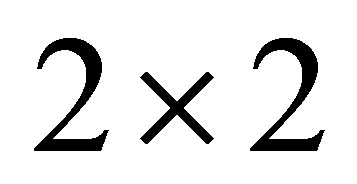 matrices. Define
matrices. Define 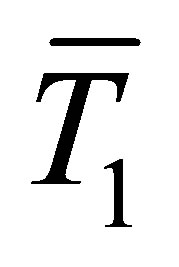 by
by
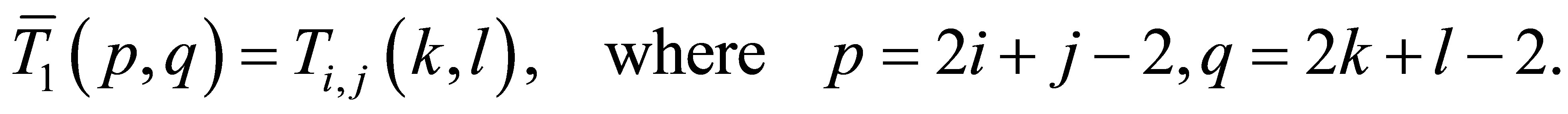 (7)
(7)
Ban and Chang [7] decomposed  as the product of
as the product of ![]() and
and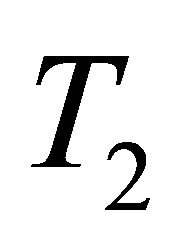 .
.
Theorem 2.2. (See [7]) Suppose 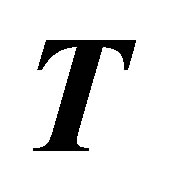 is the transition matrix of (1), and
is the transition matrix of (1), and ![]() and
and  are the transition matrices of the first and second layer, respectively. Let
are the transition matrices of the first and second layer, respectively. Let 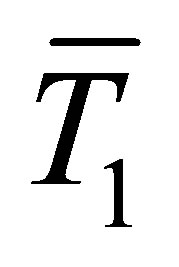 be defined as in (7). Then
be defined as in (7). Then
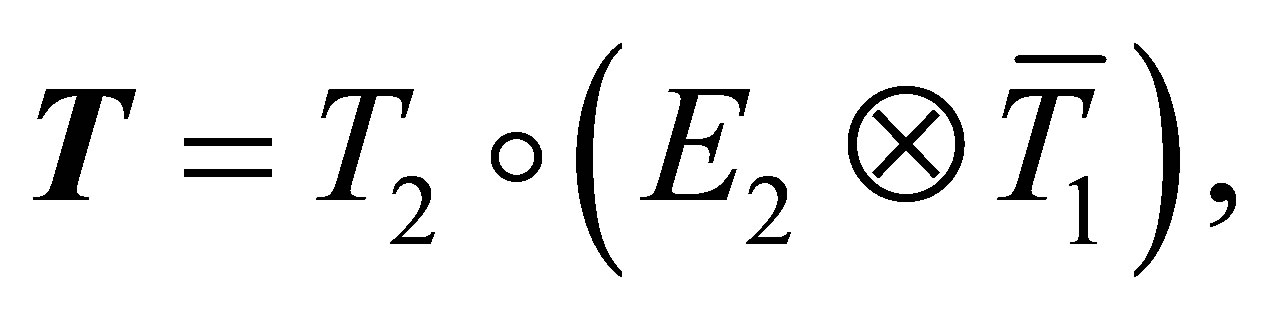 (8)
(8)
where 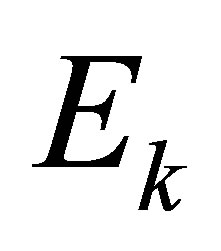 is a
is a  matrix with all entries being 1’s;
matrix with all entries being 1’s;  and
and  are the Hadamard and Kronecker product, respectively.
are the Hadamard and Kronecker product, respectively.
As being demonstrated in [7-9,13], the solution space  is a so-called shift of finite type (SFT, also known as a topological Markov shift) and the output space
is a so-called shift of finite type (SFT, also known as a topological Markov shift) and the output space  is a sofic shift. More specifically, a SFT can be represented as a directed graph
is a sofic shift. More specifically, a SFT can be represented as a directed graph 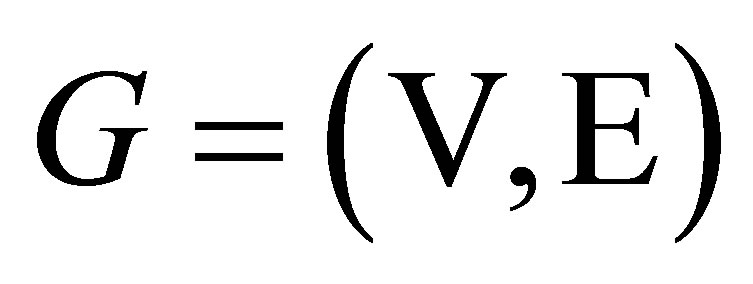 and a sofic shift can be represented as a labeled graph
and a sofic shift can be represented as a labeled graph  for some labeling
for some labeling 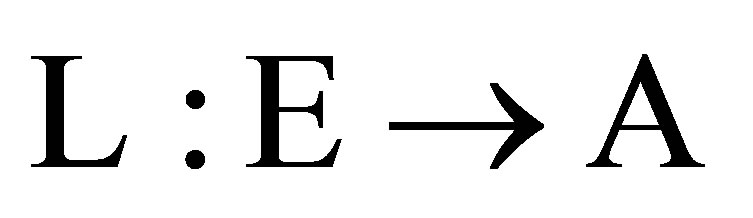 and finite alphabet
and finite alphabet . A labeled graph
. A labeled graph 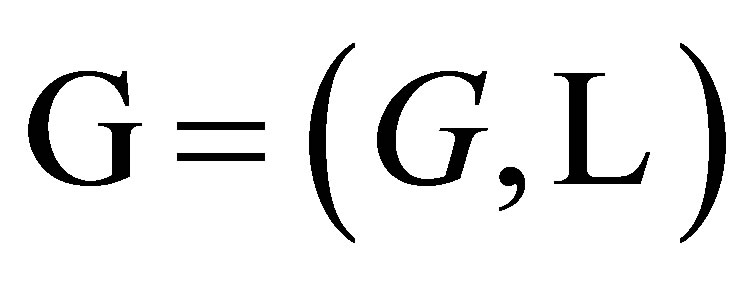 is called right-resolving if the restriction of
is called right-resolving if the restriction of  to
to  is one-to-one for all
is one-to-one for all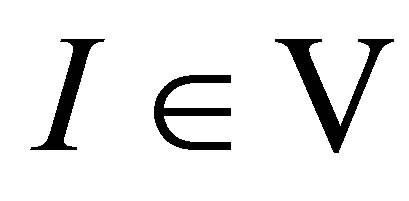 , where
, where 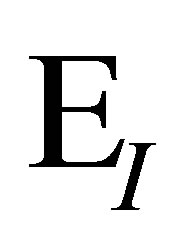 consists of those edges starting from
consists of those edges starting from . If
. If ![]() is not right-solving, there exists a labeled graph
is not right-solving, there exists a labeled graph , derived by applying subset construction method (SCM) to
, derived by applying subset construction method (SCM) to![]() , such that the sofic shift represented by
, such that the sofic shift represented by  is identical to the original space. A detailed instruction is referred to [14].
is identical to the original space. A detailed instruction is referred to [14].
One of the most frequently used quantum for the measure of the spatial complexity is the topological entropy. Let  be a symbolic space and let
be a symbolic space and let 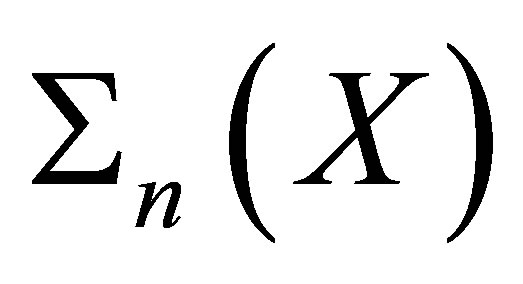 denote the collection of the patterns of length
denote the collection of the patterns of length ![]() in
in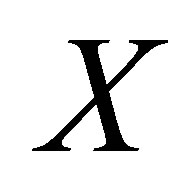 . The topological entropy of
. The topological entropy of 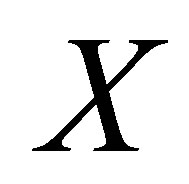 is defined by
is defined by
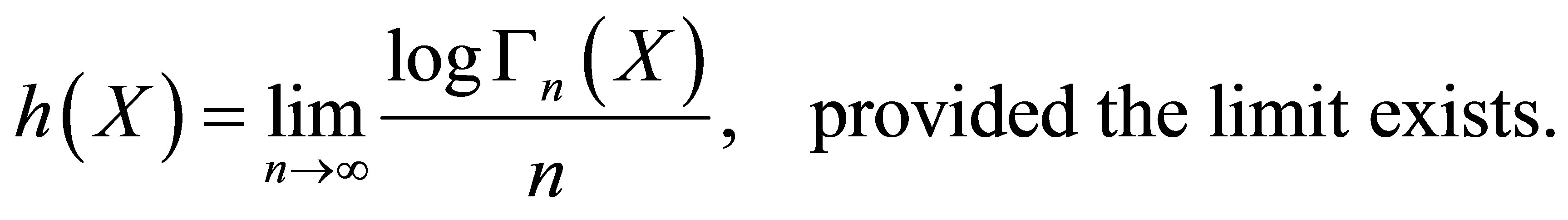
Herein
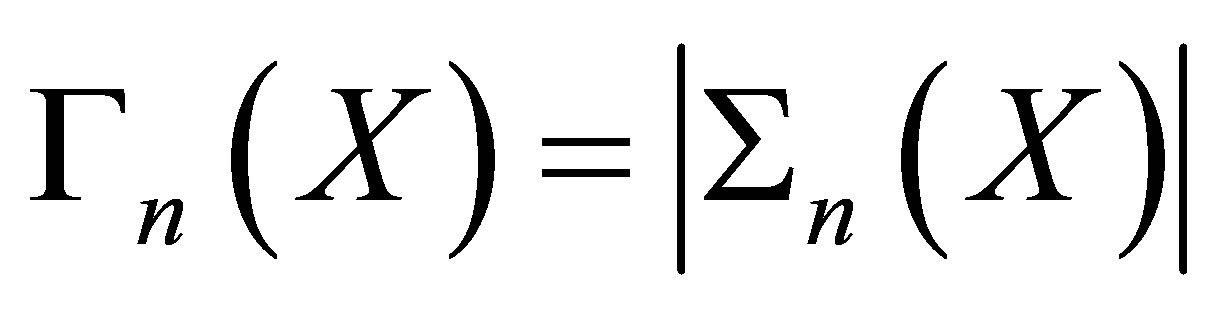
indicates the cardinality of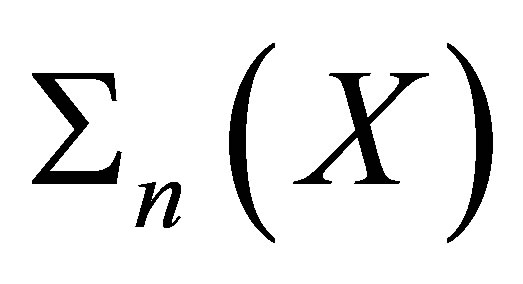 .
.
Theorem 2.3. (See [7,9,13]) Let ![]() be the labeled graph obtained from the transition matrix
be the labeled graph obtained from the transition matrix 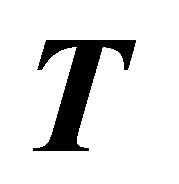 of (1). The topological entropies of
of (1). The topological entropies of  and
and  are
are 
 and
and
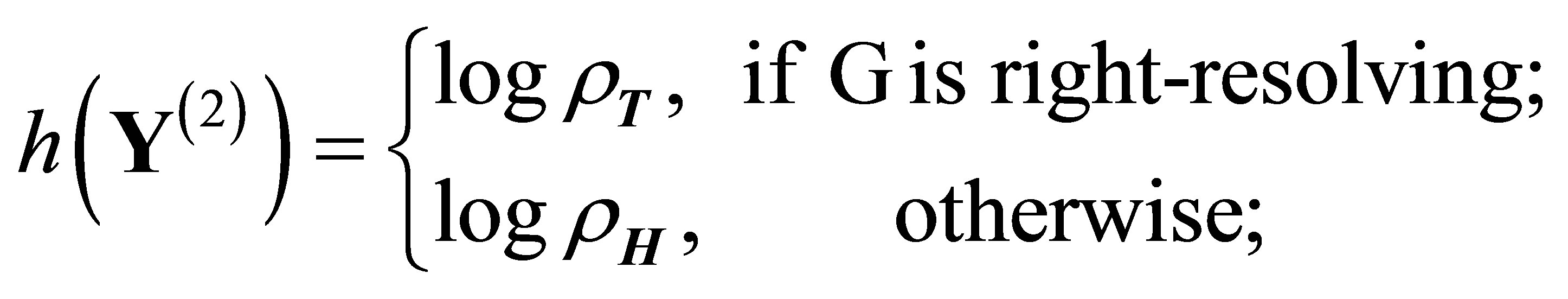 (9)
(9)
respectively, where  is the transition matrix of the labeled graph
is the transition matrix of the labeled graph  which is obtained by applying SCM to
which is obtained by applying SCM to![]() .
.
Aside from the topological entropy, the Hausdorff dimension characterizes its geometrical structure. The concept of the Hausdorff dimension generalizes the notion of the dimension of a real vector space and helps to distinguish the difference of measure zero sets. Let  be a finite set with cardinality
be a finite set with cardinality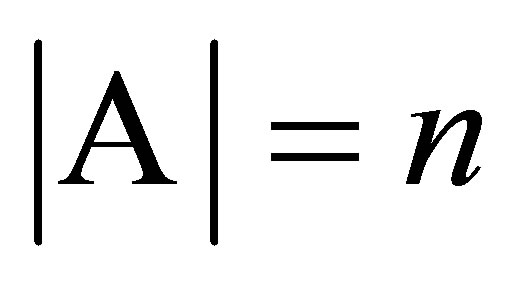 , which we consider to be an alphabet of symbols. Without the loss of generality, we usually take
, which we consider to be an alphabet of symbols. Without the loss of generality, we usually take
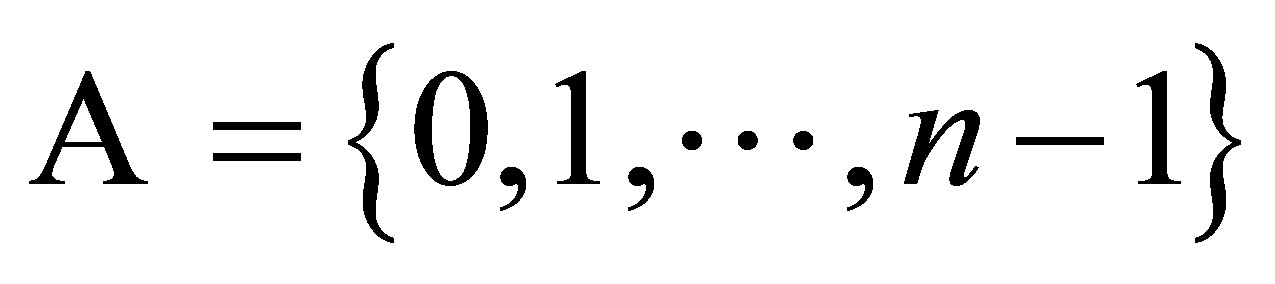 .
.
The full  -shift
-shift 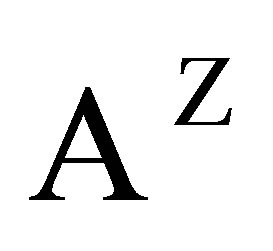 is the collection of all biinfinite sequences with entries from
is the collection of all biinfinite sequences with entries from . More precisely,
. More precisely,
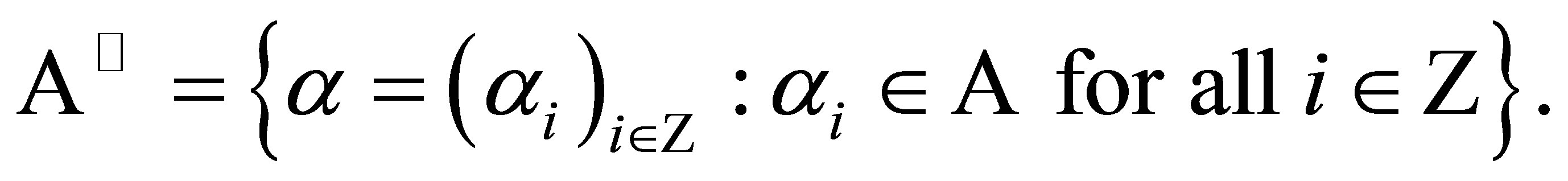
It is well-known that 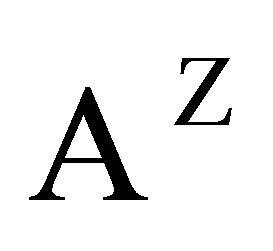 is a compact metric space endowed with the metric
is a compact metric space endowed with the metric
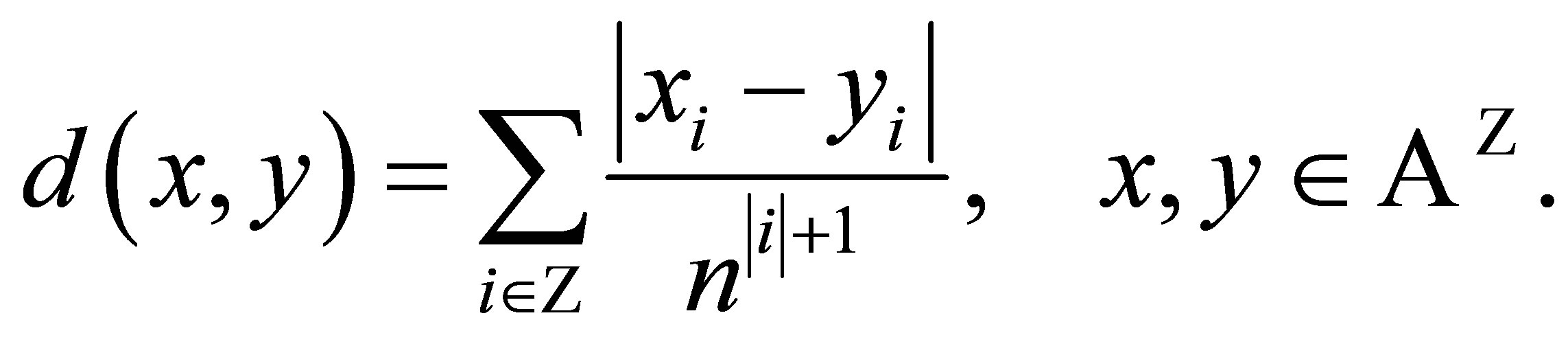
Suppose  is a subspace of
is a subspace of . Set
. Set
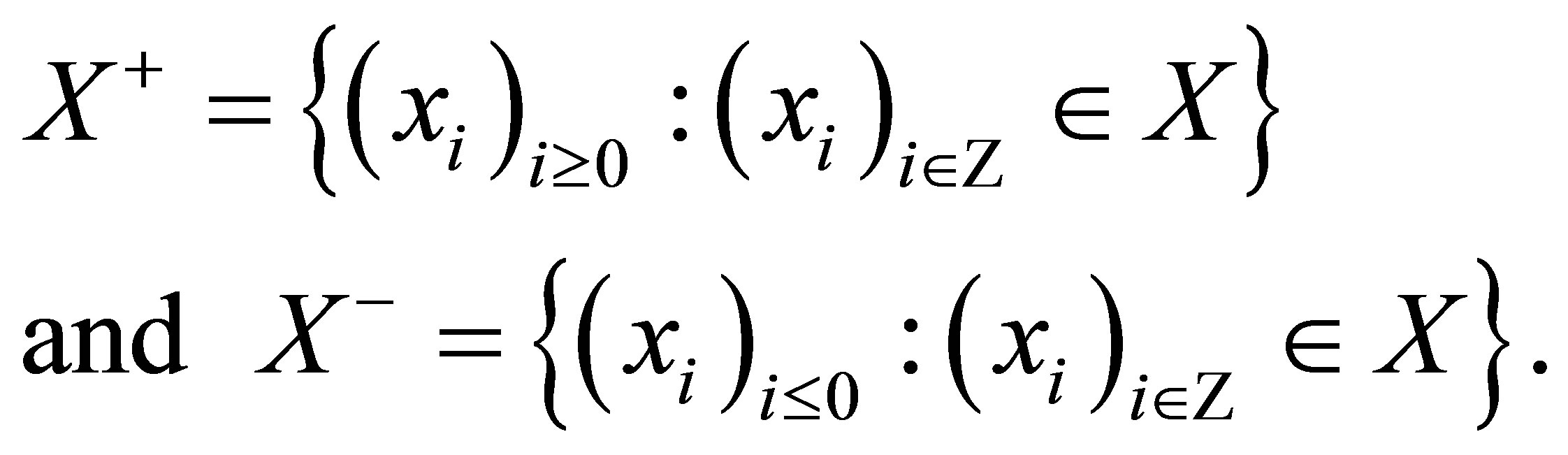
It follows that 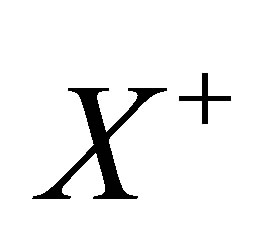 and
and  can be embedded in the close interval
can be embedded in the close interval 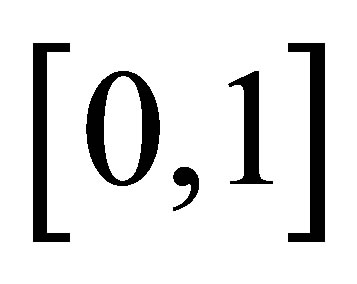 separately. Moreover,
separately. Moreover,  and
and 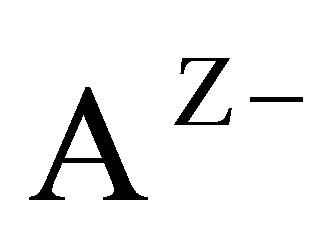 can be mapped onto the close interval
can be mapped onto the close interval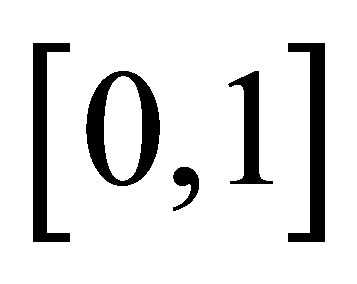 , and
, and 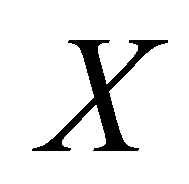 is identified with the direct product
is identified with the direct product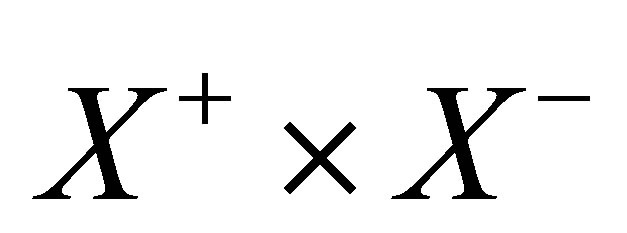 . This makes the elucidation of the Hausdorff dimension of the output space
. This makes the elucidation of the Hausdorff dimension of the output space 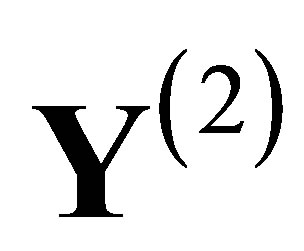 comprehensible. (Recall that the alphabet
comprehensible. (Recall that the alphabet  of
of 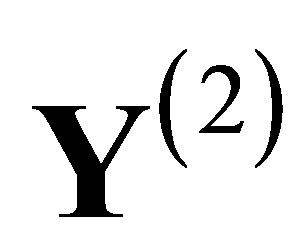 is
is ).
).
2.2. Main Result
Suppose 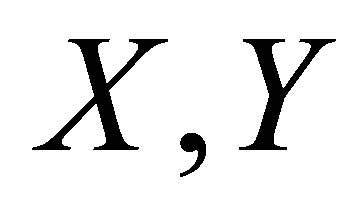 are shift spaces and
are shift spaces and  is a factor map. We say that
is a factor map. We say that  has a synchronizing word if there is a finite word
has a synchronizing word if there is a finite word  such that each element in
such that each element in 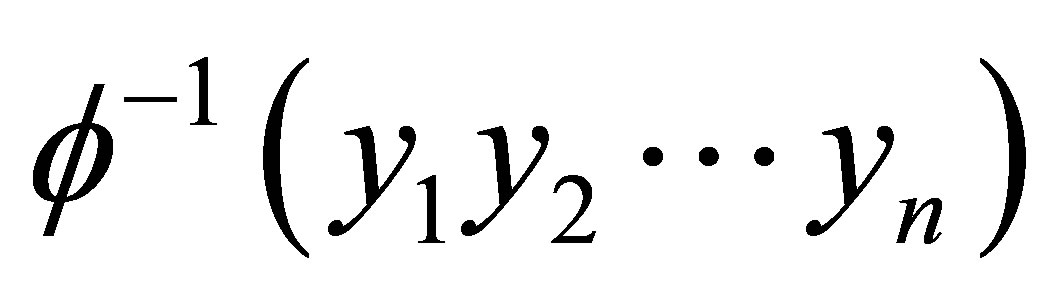 admits the same terminal entry. More precisely, for any
admits the same terminal entry. More precisely, for any
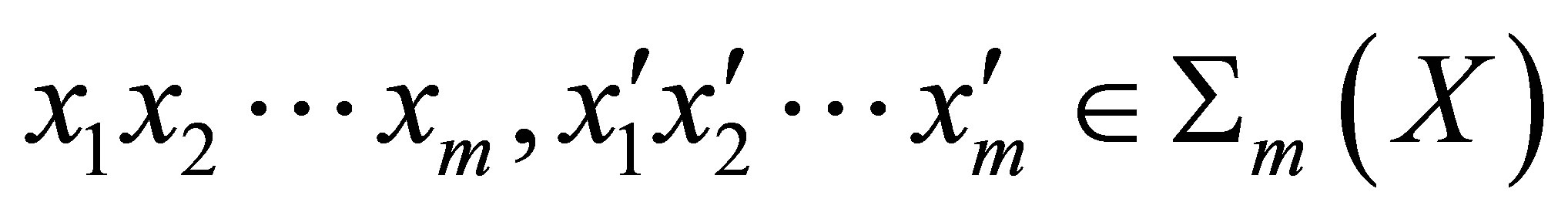
satisfying
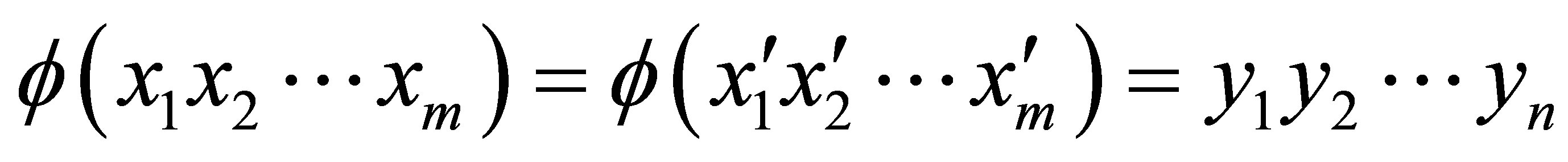 we have
we have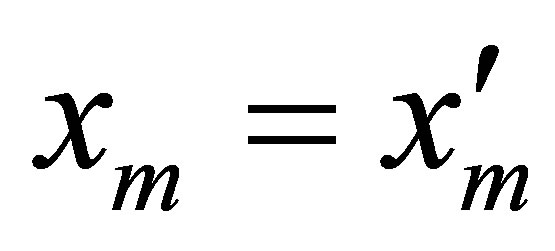 .
.
Suppose  is a labeled graph representation of the output space
is a labeled graph representation of the output space 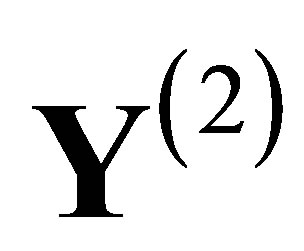 of (1). Denote by
of (1). Denote by 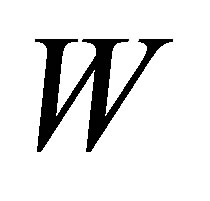 the SFT represented by the graph
the SFT represented by the graph 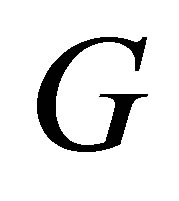 if
if ![]() is right-resolving; otherwise, denote by
is right-resolving; otherwise, denote by 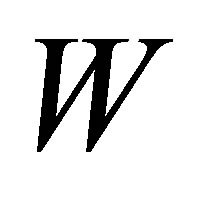 the SFT represented by the graph
the SFT represented by the graph , where
, where 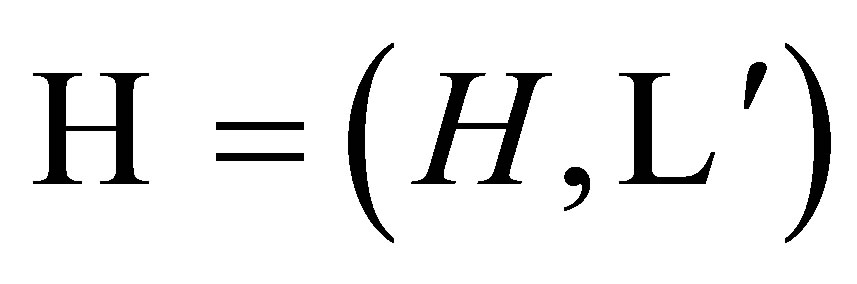 is obtained by applying SCM to
is obtained by applying SCM to![]() . It follows that
. It follows that 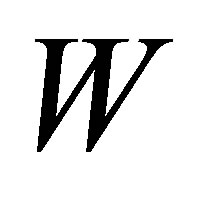 is a covering space of
is a covering space of 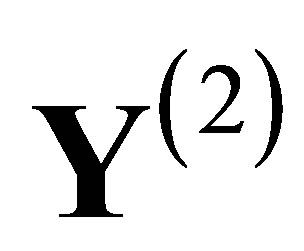 and there is a factor map
and there is a factor map 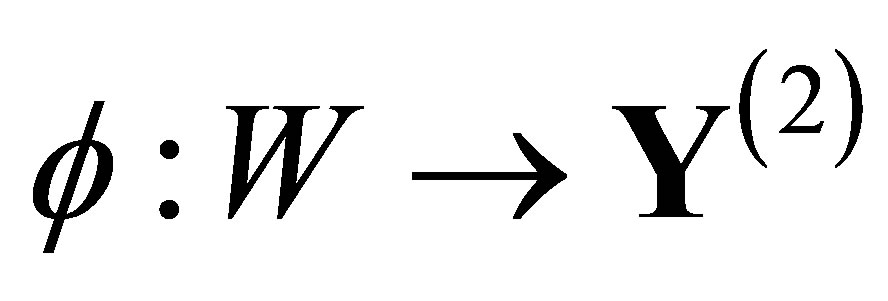 which is represented by the labeling
which is represented by the labeling 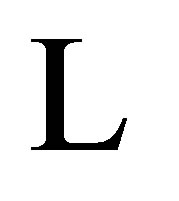 (or
(or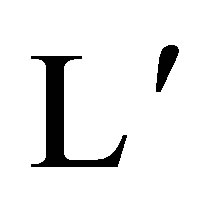 ). Theorem 2.4 asserts that the Hausdorff dimension of the output space
). Theorem 2.4 asserts that the Hausdorff dimension of the output space 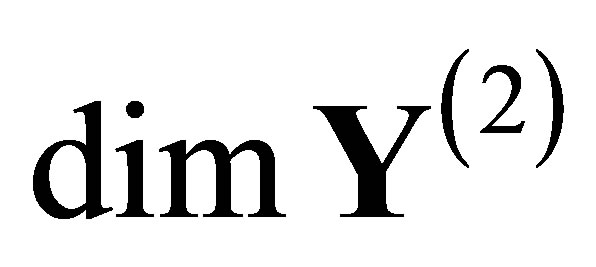 relates to the topological entropy of its covering space
relates to the topological entropy of its covering space 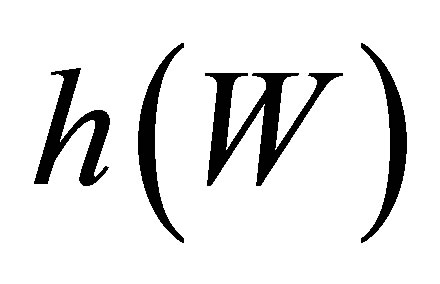 if
if  has a synchronizing word.
has a synchronizing word.
Theorem 2.4. Along with the same assumption of Theorem 2.3. Let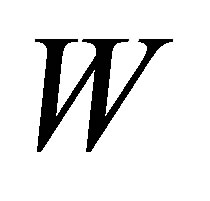 , which is represented by
, which is represented by 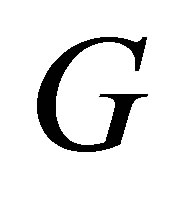 if
if ![]() is right-resolving and is represented by
is right-resolving and is represented by  otherwise, be the covering space of
otherwise, be the covering space of . Suppose the factor map
. Suppose the factor map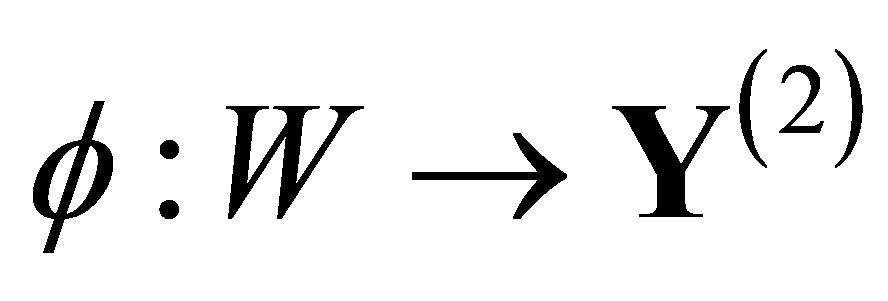 , which is represented by the labeling
, which is represented by the labeling 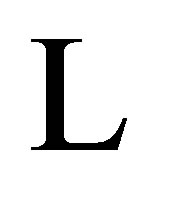 (or
(or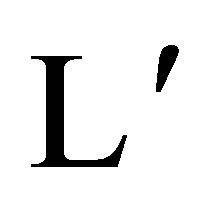 ), has a synchronizing word. Then
), has a synchronizing word. Then
 (10)
(10)
Restated,
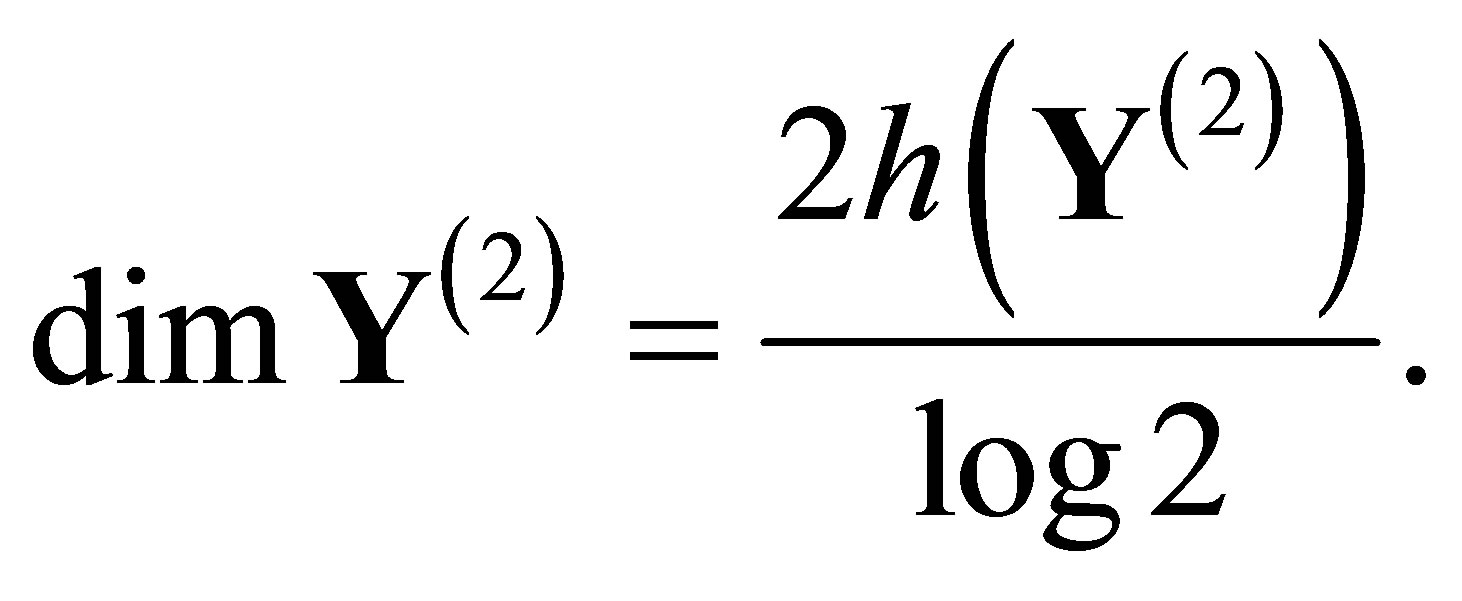 (11)
(11)
Proof. Suppose 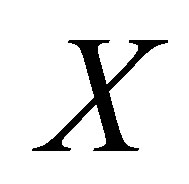 is a SFT and
is a SFT and  is an invariant probability measure on
is an invariant probability measure on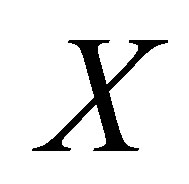 . The Variational Principle indicates that the topological entropy of
. The Variational Principle indicates that the topological entropy of 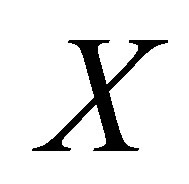 is the supremum of the measure-theoretic entropy of
is the supremum of the measure-theoretic entropy of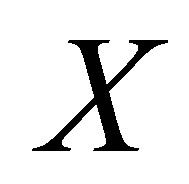 ; more precisely,
; more precisely,

A measure 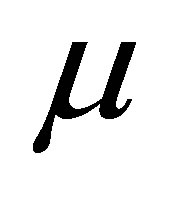 is called maximal if
is called maximal if 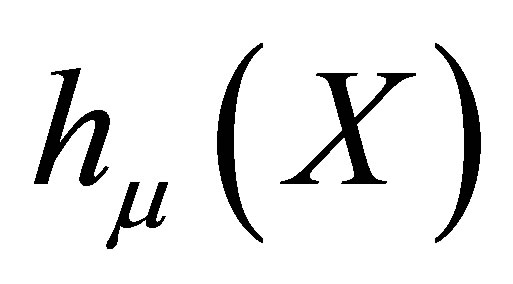 attains the supremum. Let
attains the supremum. Let 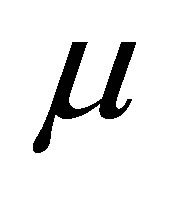 be a Markov measure which is derived from the transition matrix of
be a Markov measure which is derived from the transition matrix of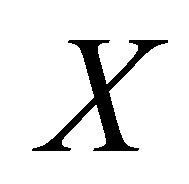 . Then
. Then 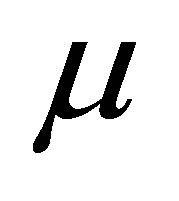 is the unique measure that satisfies
is the unique measure that satisfies
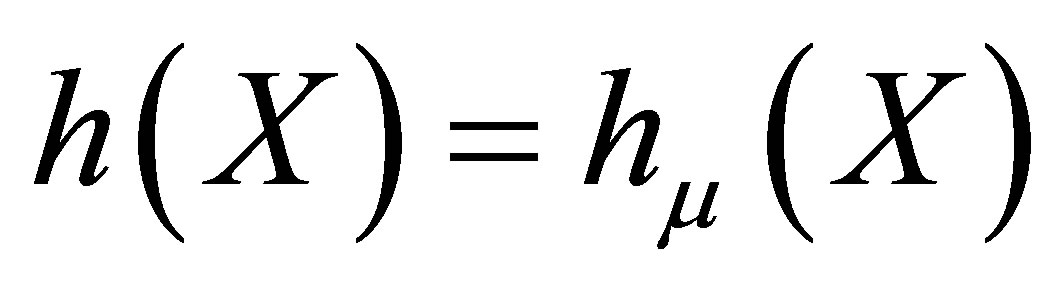
if 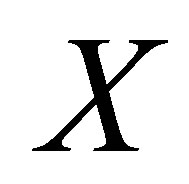 is topologically transitive (cf. [15]). Ban and Chang showed that, if
is topologically transitive (cf. [15]). Ban and Chang showed that, if 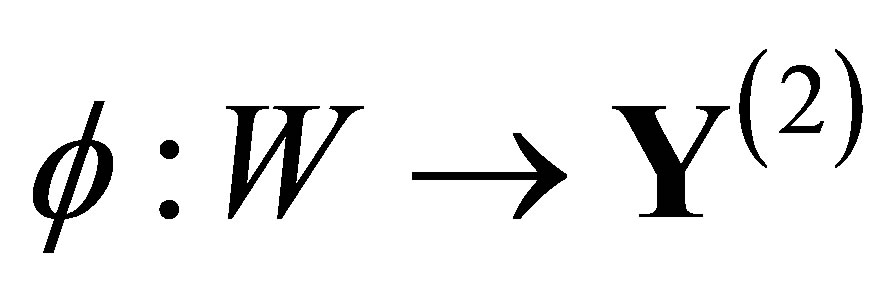 has a synchronizing word, then the Hausdorff dimension of the output space is
has a synchronizing word, then the Hausdorff dimension of the output space is
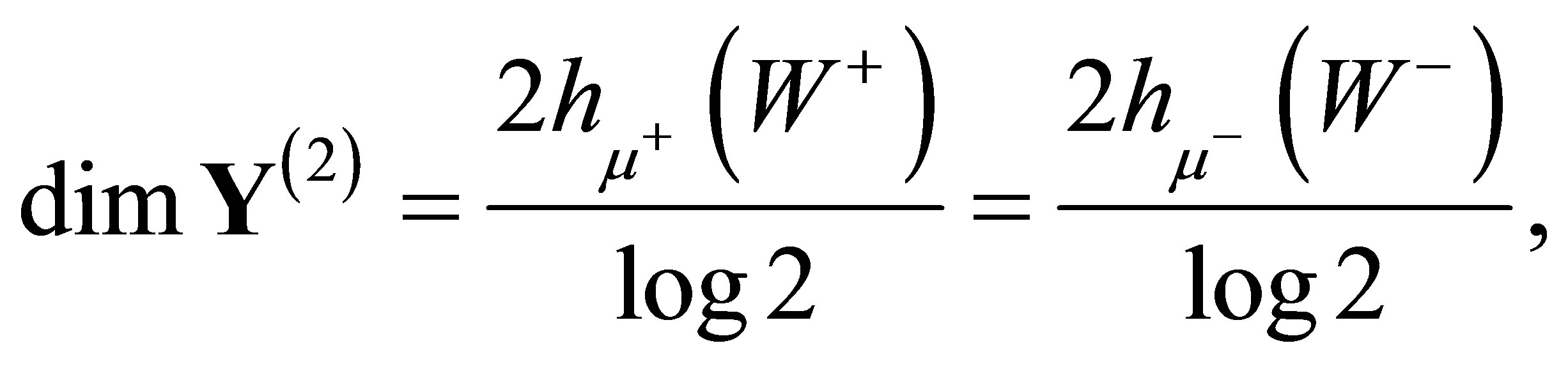
where  is a maximal measure of
is a maximal measure of  (see [16], Theorem 2.6). Since
(see [16], Theorem 2.6). Since  is right-resolving, the factor map
is right-resolving, the factor map  is finite-to-one. It follows that
is finite-to-one. It follows that
 .
.
Theorem 2.3 demonstrates that the topological entropy of the output space

(respectively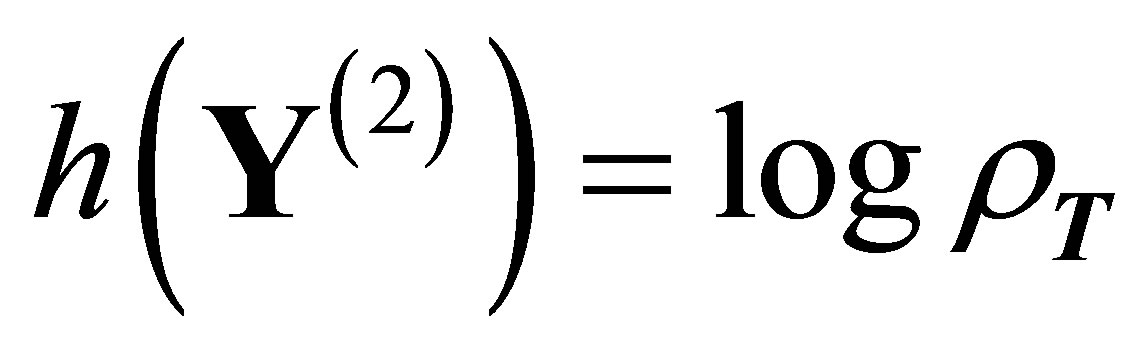 ) if
) if ![]() is not rightresolving (respectively
is not rightresolving (respectively ![]() is right-resolving). A straightforward examination infers that
is right-resolving). A straightforward examination infers that
 .
.
Hence we have

this completes the proof. 
3. Example
Suppose 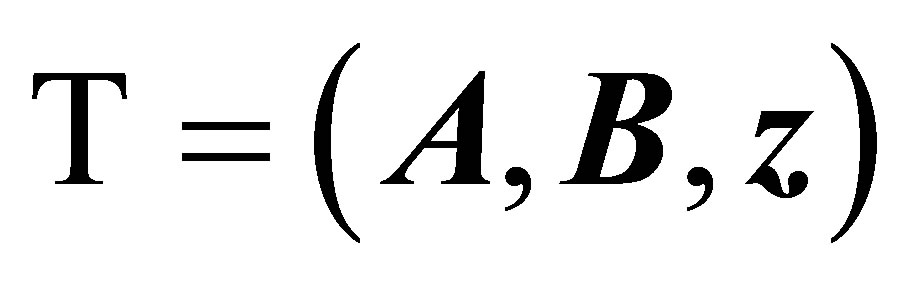 with
with
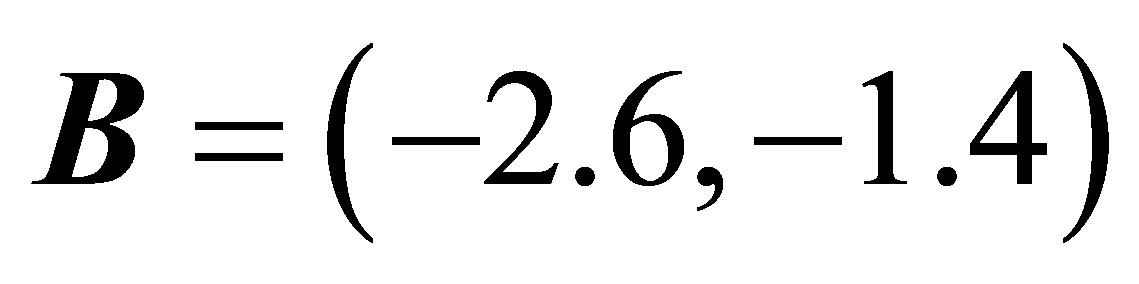

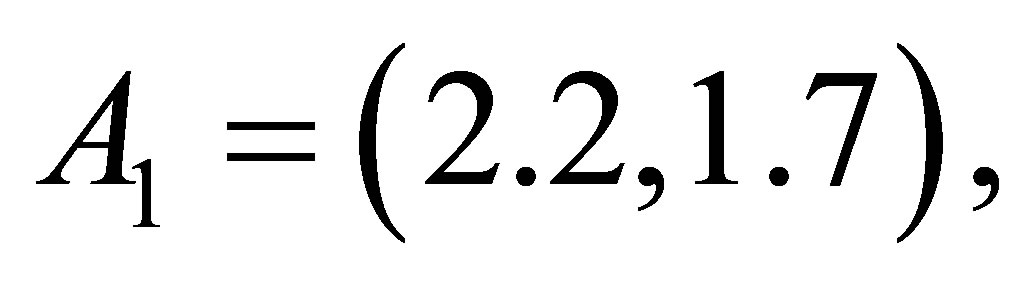 and
and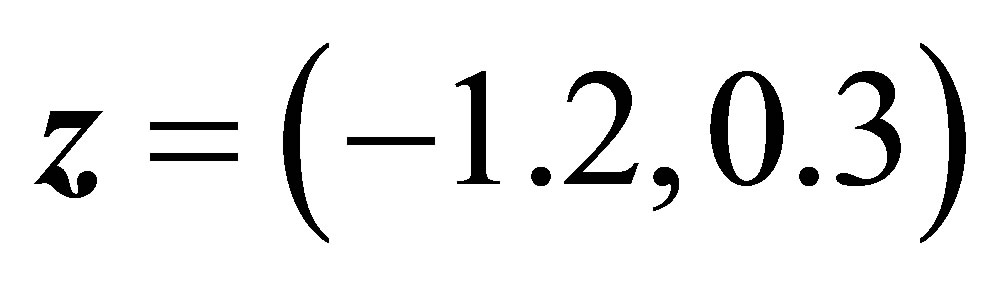 . The transition matrices for the first and second layer are
. The transition matrices for the first and second layer are
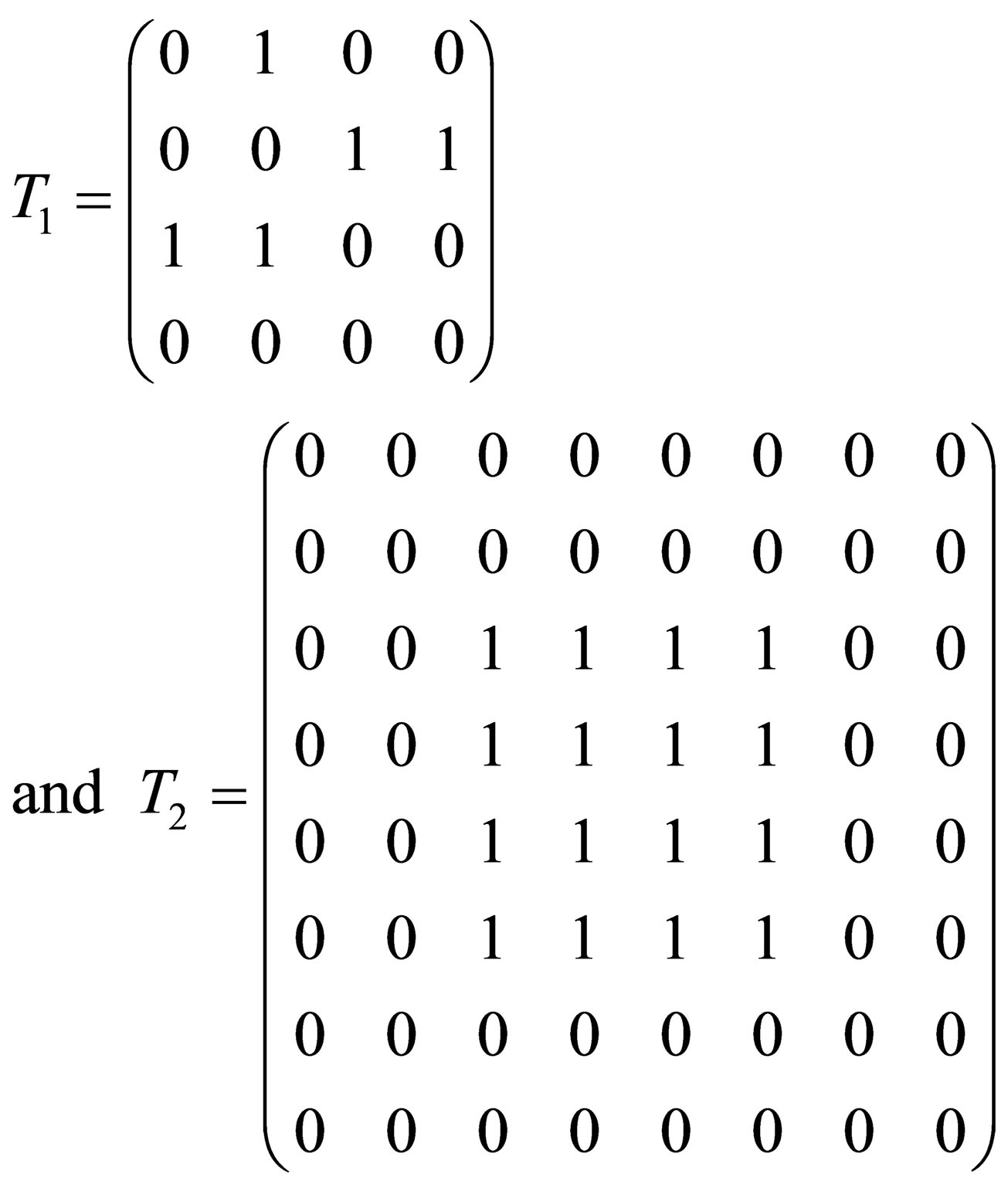
respectively. Therefore, the transition matrix and the symbolic transition matrix of the MNN are
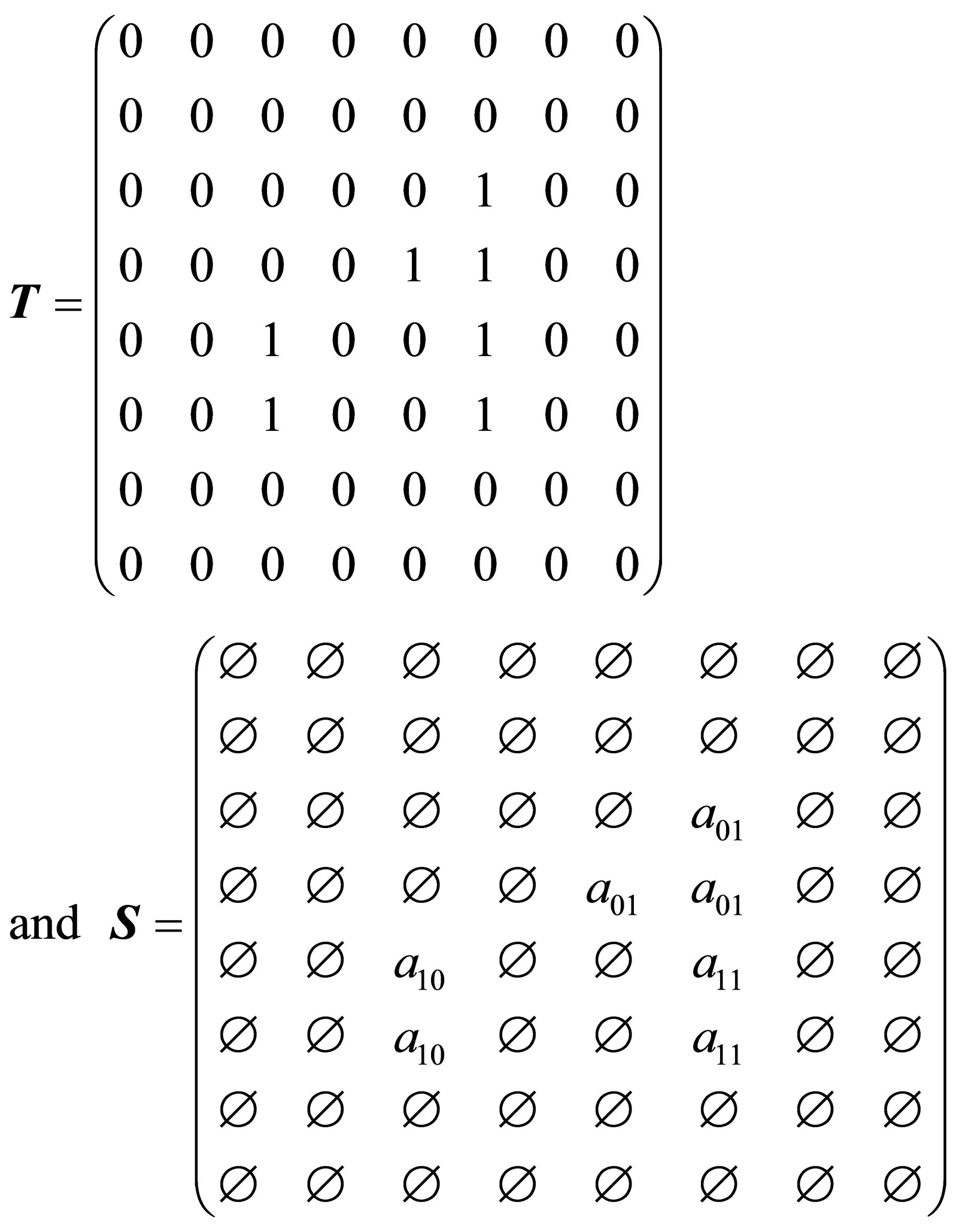
respectively, where
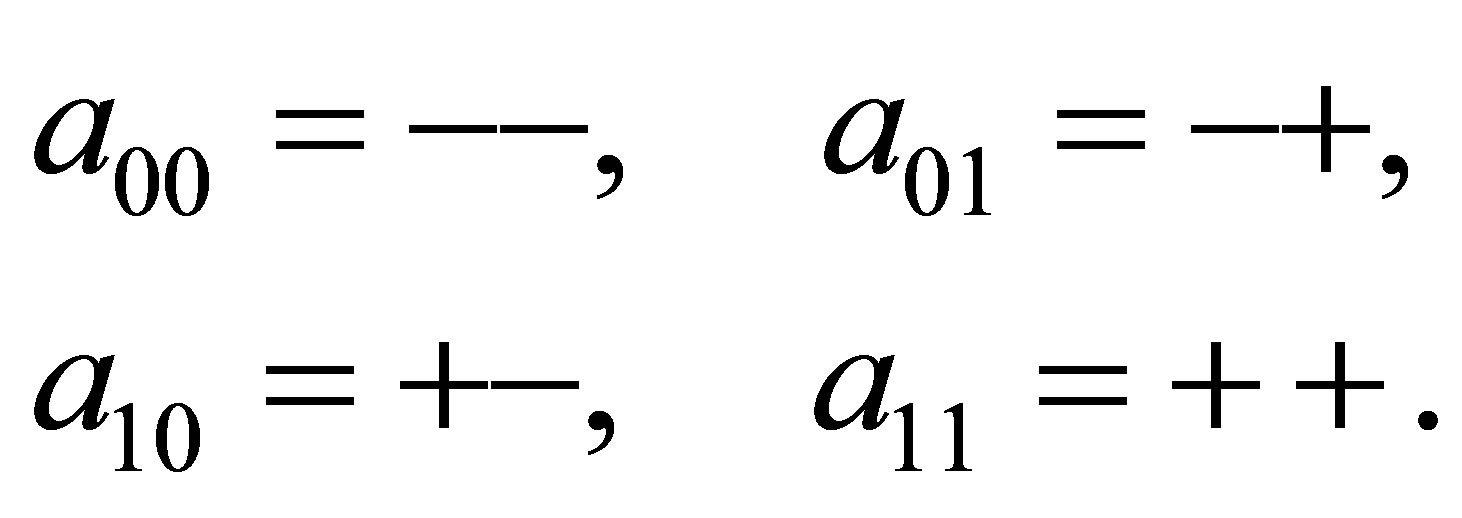
It is seen from the symbolic transition matrix  that the labeled graph
that the labeled graph ![]() is not right-resolving, and applying SMC to
is not right-resolving, and applying SMC to ![]() derives a right-resolving labeled graph
derives a right-resolving labeled graph  (cf. Figure 1). The transition matrix of
(cf. Figure 1). The transition matrix of , indexed by
, indexed by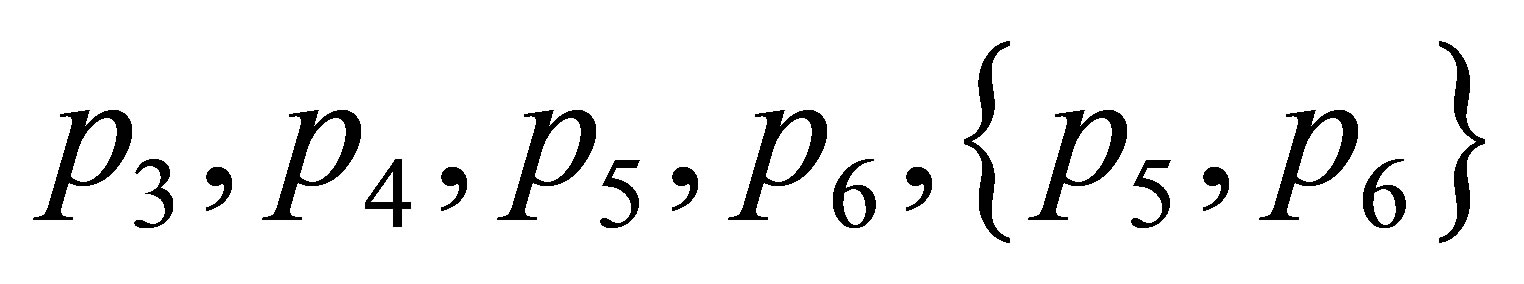 , is
, is

Theorem 2.3 indicates that
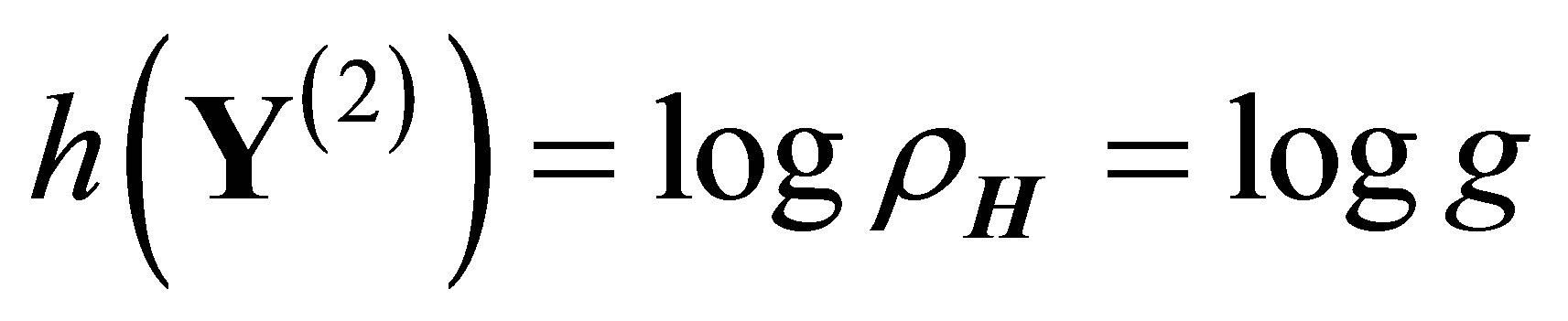 where
where

is the golden mean.
The symbolic transition matrix of  is
is
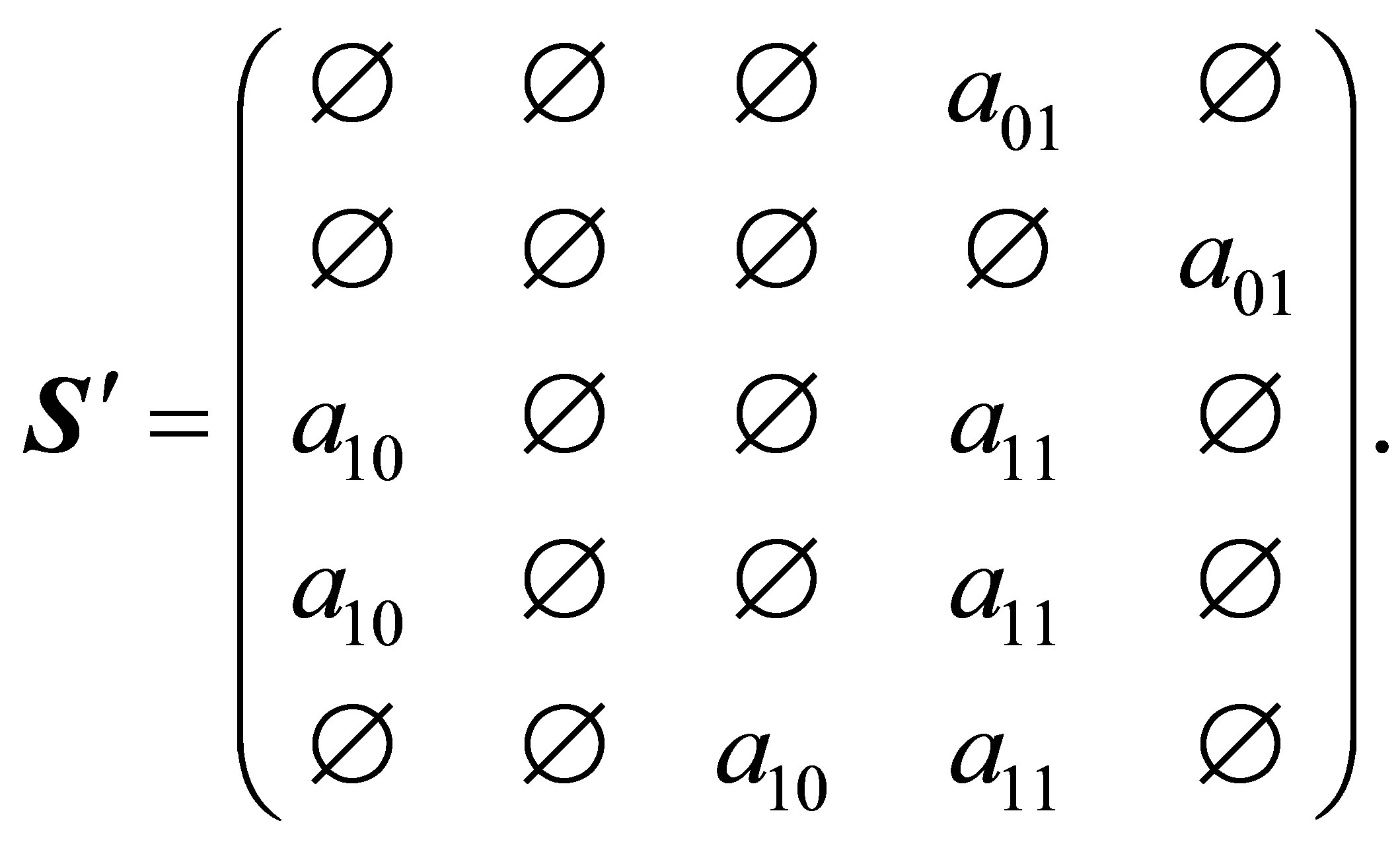
It is seen that both  and
and  are synchronizing words of
are synchronizing words of . Theorem 2.4 demonstrates that
. Theorem 2.4 demonstrates that

The fractal set of the output space  is seen in Figure 2.
is seen in Figure 2.

Figure 1. The right-resolving labeled graph  obtained by applying SCM to
obtained by applying SCM to ![]() in example. Here
in example. Here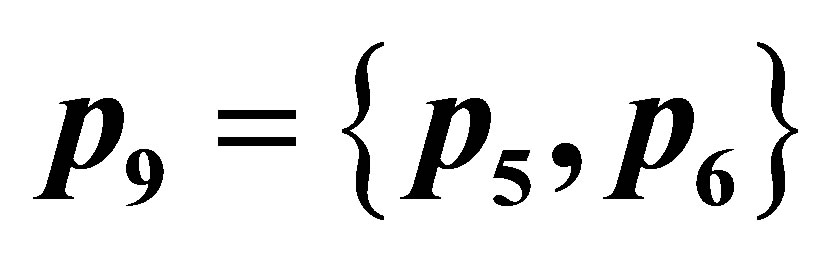 .
.
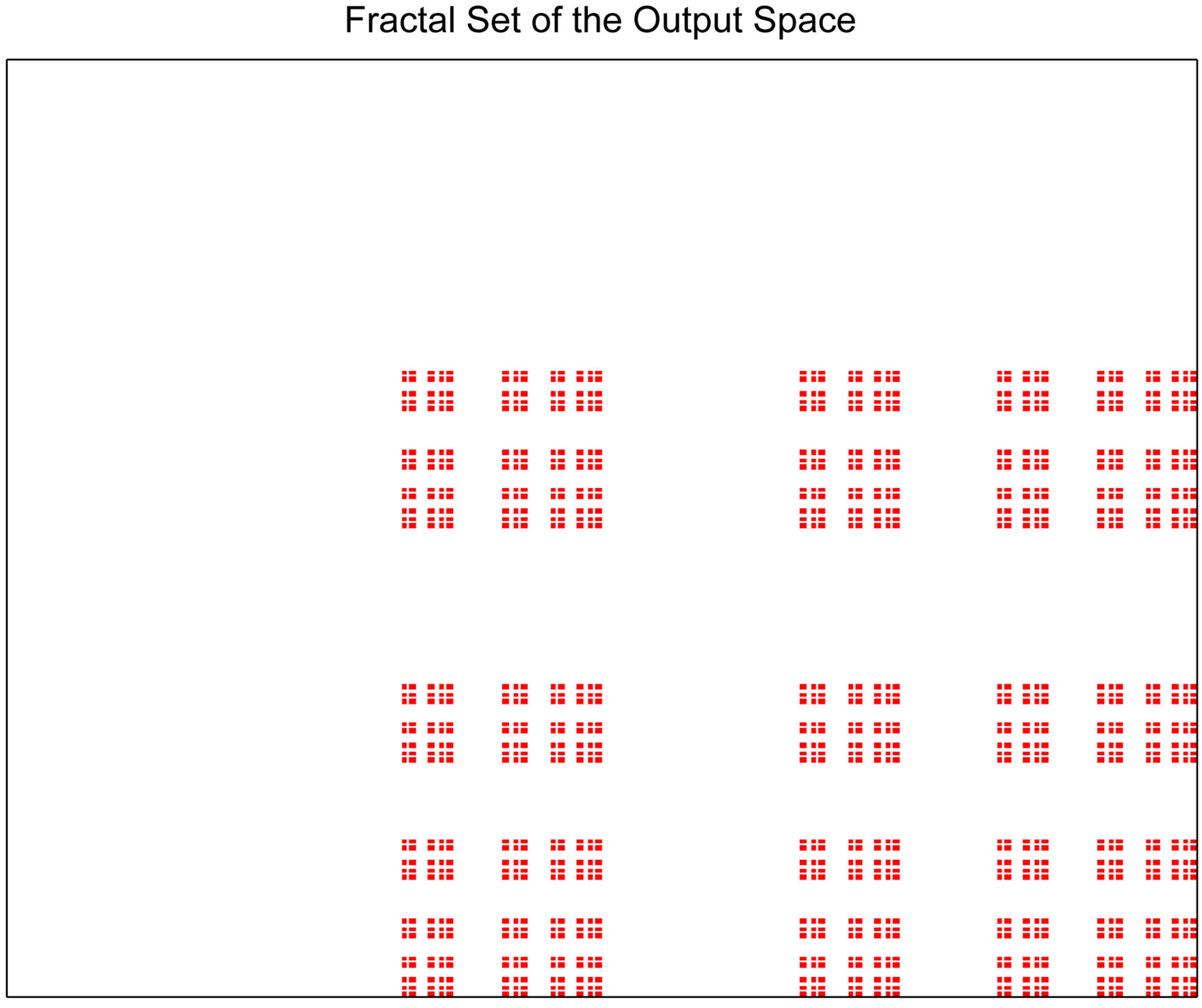
Figure 2. The fractal set of the output space .
.
REFERENCES
- K. Hornik, M. Stinchcombe and H. White, “Multilayer Feedforward Networks Are Universal Approximators,” Neural Networks, Vol. 2, No. 5, 1989, pp. 359-366. http://dx.doi.org/10.1016/0893-6080(89)90020-8
- B. Widrow and M. Lehr, “30 Years of Adaptive Neural Networks: Perceptron Madaline, and Backpropagation,” Proceedings of the IEEE, Vol. 78, No. 9, 1990, pp. 1415- 1442. http://dx.doi.org/10.1109/5.58323
- Y. A. Alsultanny and M. M. Aqul, “Pattern Recognition Using Multilayer Neural-Genetic Algorithm,” Neurocomputing, Vol. 51, 2003, pp. 237-247. http://dx.doi.org/10.1016/S0925-2312(02)00619-7
- B. Widrow, “Layered Neural Nets for Pattern Recognition,” IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 36, No. 7, 1962, pp. 1109-1118. http://dx.doi.org/10.1109/29.1638
- J. J. Hopeld and D. W. Tank, “Neural Computation of Decisions in Optimization Problems,” Biological Cybernetics, Vol. 52, No. 3, 1985, pp. 141-152.
- C. Peterson and B. Soderberg, “A New Method for Mapping Optimization Problems onto Neural Network,” International Journal of Neural Systems, Vol. 1, 1989, pp. 3-22. http://dx.doi.org/10.1142/S0129065789000414
- J.-C. Ban and C.-H. Chang, “The Learning Problem of Multi-Layer Neural Networks,” Neural Networks, Vol. 46, 2013, pp. 116-123. http://dx.doi.org/10.1016/j.neunet.2013.05.006
- J.-C. Ban, C.-H. Chang and S.-S. Lin, “The Structure of Multi-Layer Cellular Neural Networks,” Journal of Differential Equations, Vol. 252, No. 8, 2012, pp. 4563-4597. http://dx.doi.org/10.1016/j.jde.2012.01.006
- J.-C. Ban, C.-H. Chang, S.-S. Lin and Y.-H. Lin, “Spatial Complexity in Multi-Layer Cellular Neural Networks,” Journal of Differential Equations, Vol. 246, No. 2, 2009, pp. 552-580. http://dx.doi.org/10.1016/j.jde.2008.05.004
- S.-N. Chow and J. Mallet-Paret, “Pattern Formation and Spatial Chaos in Lattice Dynamical Systems: I and II,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, Vol. 42, No. 10, 1995, pp. 746-756. http://dx.doi.org/10.1109/81.473583
- K. Falconer, “Fractal Geometry: Mathematical Foundations and Application,” 2nd Edition, John Wilet & Sons, New York, London, Sydney, 2003. http://dx.doi.org/10.1002/0470013850
- Y. Pesin, “Dimension Theory in Dynamical Systems: Contemporary Views and Application,” The University of Chicago Press, Chicago, 1997. http://dx.doi.org/10.7208/chicago/9780226662237.001.0001
- J. Juang and S.-S. Lin, “Cellular Neural Networks: Mosaic Pattern and Spatial Chaos,” SIAM Journal on Applied Mathematics, Vol. 60, No. 3, 2000, pp. 891-915. http://dx.doi.org/10.1137/S0036139997323607
- D. Lind and B. Marcus, “An Introduction to Symbolic Dynamics and Coding,” Cambridge University Press, Cambridge, 1995. http://dx.doi.org/10.1017/CBO9780511626302
- B. Kitchens, “Symbolic Dynamics. One-Sided, Two-Sided and Countable State Markov Shifts,” Springer-Verlag, New York, 1998.
- J.-C. Ban and C.-H. Chang, “On the Structure of MultiLayer Cellular Neural Networks. Part II: The Complexity between Two Layers,” Submitted, 2012.
NOTES
*Ban is partially supported by the National Science Council (Contract No NSC 100-2115-M-259-009-MY2).
#Chang is grateful for the partial support of the National Science Council (Contract No NSC 101-2115-M-035-002-).
1Pesin showed that the box dimension of a shift space ![]() is the quotient of the topological entropy and the metric on
is the quotient of the topological entropy and the metric on![]() . More precisely, if the metric is defined by
. More precisely, if the metric is defined by 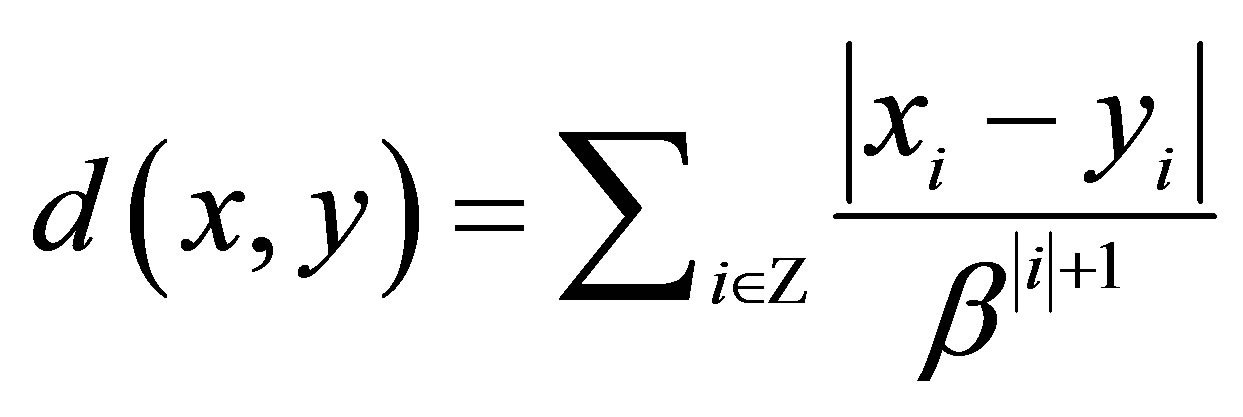 for
for , then the box dimension is
, then the box dimension is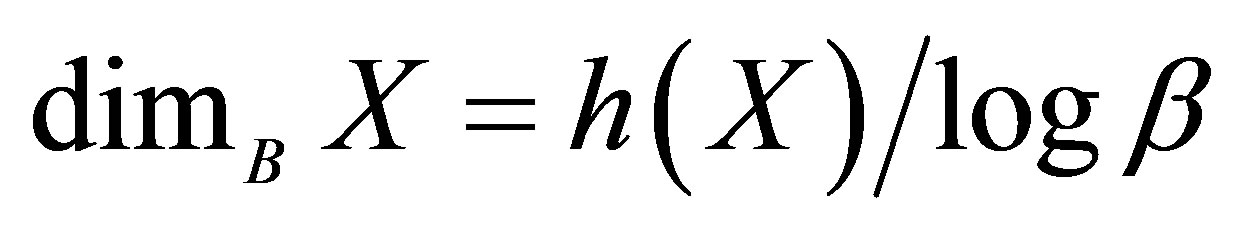 .
.

