Advances in Pure Mathematics
Vol.3 No.5(2013), Article ID:35056,7 pages DOI:10.4236/apm.2013.35064
Global Existence, Uniqueness of Weak Solutions and Determining Functionals for Nonlinear Wave Equations
Department of Mathematics, Gazi University, Ankara, Turkey
Email: ulku@gazi.edu.tr
Copyright © 2013 Ülkü Dinlemez. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 21, 2013; revised May 30, 2013; accepted July 3, 2013
Keywords: Global Existence; Uniqueness; Determining Modes
ABSTRACT
We consider the initial-boundary value problem for a nonlinear wave equation with strong structural damping and nonlinear source terms in IR. We prove the global existence and uniqueness of weak solutions of the problem and then we will study the determining modes on the phase space 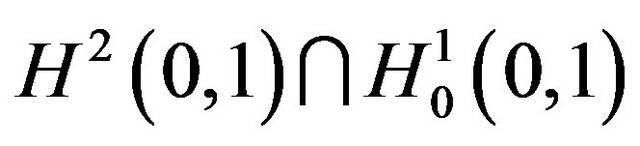 by using energy methods and the concept of the completeness defect.
by using energy methods and the concept of the completeness defect.
1. Introduction
In this paper we study the initial-boundary value problem for the following nonlinear wave equation
 (1.1)
(1.1)
with boundary conditions
 (1.2)
(1.2)
and initial conditions
 (1.3)
(1.3)
where 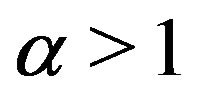 constant,
constant, 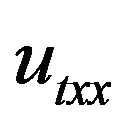 is a strong structural damping term,
is a strong structural damping term, 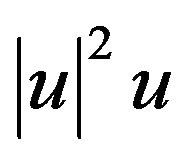 is nonlinear source term and
is nonlinear source term and 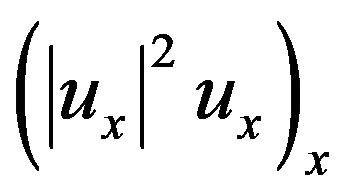 is a nonlinear strain term.
is a nonlinear strain term.
An other version of problems (1.1)-(1.3) was studied in [1-4]. In [1] Chen et al worked that the following initial boundary value problem
 (1.4)
(1.4)
 (1.5)
(1.5)
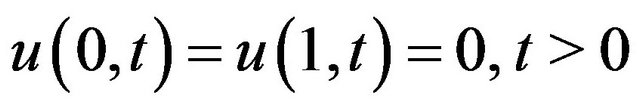 (1.6)
(1.6)
has a global solution and there exists a compact global attractor with finite dimension. In [2] Karachalios and Staurakalis studied the local existence for (1.1) with 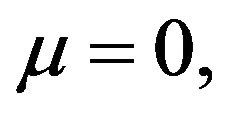 ut is a damping term and without nonlinear source term. In [3] Çelebi and Uğurlu gave the existence of a wide collection of finite sets of functionals on the phase space
ut is a damping term and without nonlinear source term. In [3] Çelebi and Uğurlu gave the existence of a wide collection of finite sets of functionals on the phase space 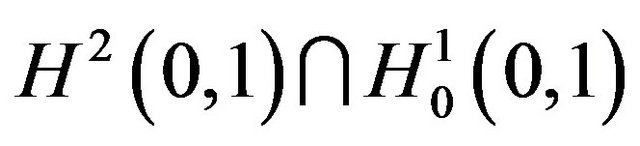 that completely determines asymptotic behavior of solutions to the strongly damped nonlinear wave equations. In [4] Chueshov presented the approach of a set of determining functionals containing determining modes and nodes that completely determines the long-time behavior of some first and second order evolution equations.
that completely determines asymptotic behavior of solutions to the strongly damped nonlinear wave equations. In [4] Chueshov presented the approach of a set of determining functionals containing determining modes and nodes that completely determines the long-time behavior of some first and second order evolution equations.
Similar results of determining modes for similar equations have been obtained in [5-7].
In this article, we take the problem defined by (1.1)- (1.3) which was not investigated in above mentioned articles. Our problem has nonlinear strain and source terms. The control of long time behavior is achieved due to the presence of restoring forces 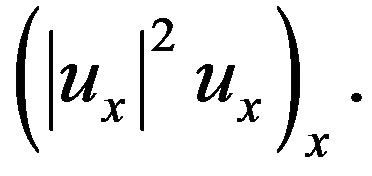 In Section 2 under conditions
In Section 2 under conditions
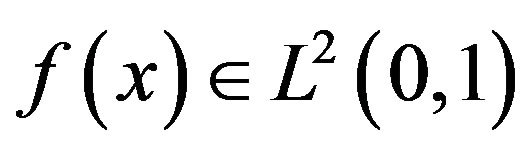
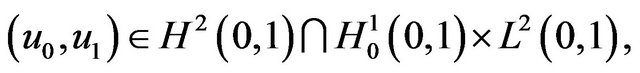 and
and 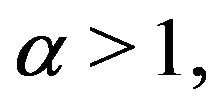 we prove the global existence and uniqueness of a weak solution u of the problems (1.1)-(1.3). In Section 3 we study determining modes on the phase space
we prove the global existence and uniqueness of a weak solution u of the problems (1.1)-(1.3). In Section 3 we study determining modes on the phase space  by using energy methods and the concept of the completeness defect.
by using energy methods and the concept of the completeness defect.
2. The Global Existence and Uniqueness of Weak Solutions
Let  be the usual Hilbert space of square integrable functions with the standard
be the usual Hilbert space of square integrable functions with the standard 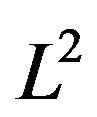 norm
norm 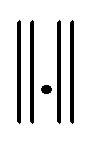 and inner product
and inner product 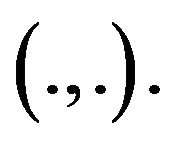 Denote
Denote 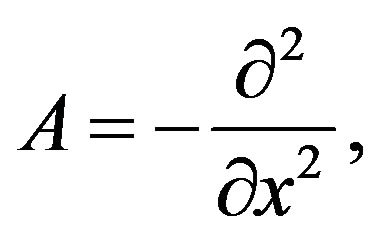 the Laplacian operator on L2 with domain
the Laplacian operator on L2 with domain  A is a sectorial operator and that
A is a sectorial operator and that 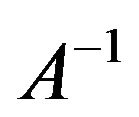 is a bounded linear operator defined in
is a bounded linear operator defined in 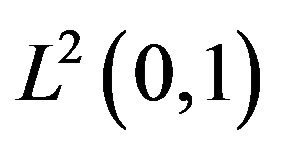 see [8]. The nonlinear source term
see [8]. The nonlinear source term 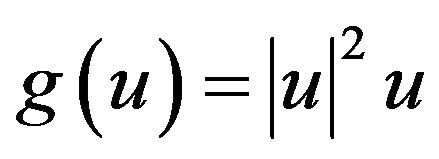 satisfies the following conditions
satisfies the following conditions
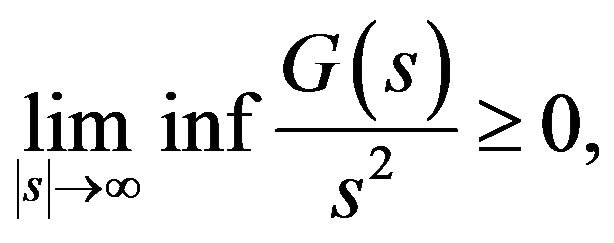
there exists a constant 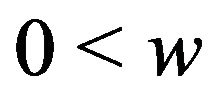 such that
such that
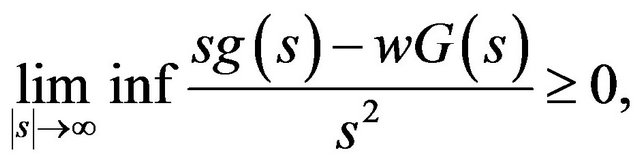
where 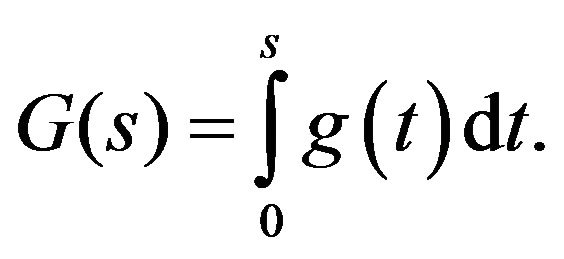 Finally we denote
Finally we denote
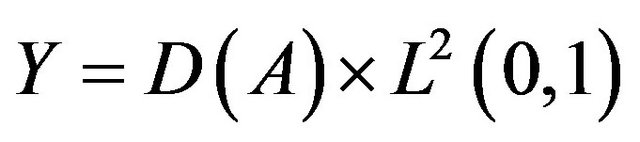 with the standard product norm
with the standard product norm
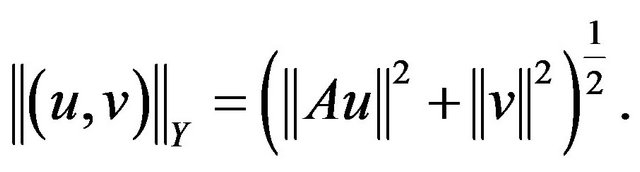 Define
Define 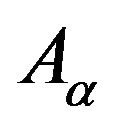 in Y by
in Y by
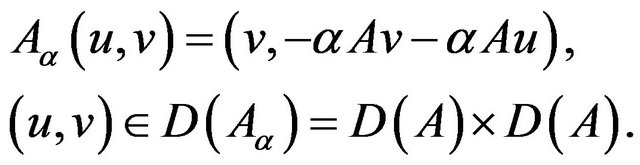 (2.1)
(2.1)
Then the following Lemma1 is valid [9].
Lemma 1 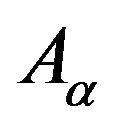 is a sectorial operator on Y.
is a sectorial operator on Y.
We define a map 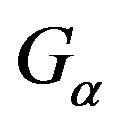 from
from 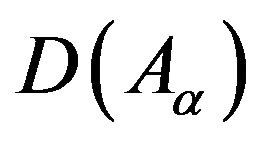 to Y by
to Y by
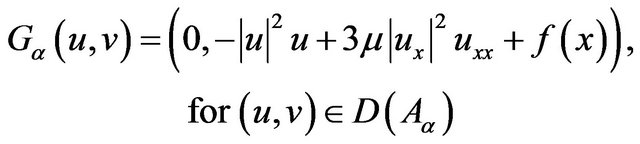 (2.2)
(2.2)
where 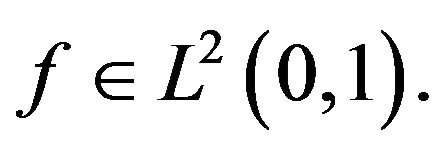
Using the Sobolev embedding theorem, we can see that 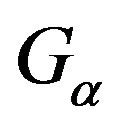 is locally Lipschitz continuous. Thus we apply the existence theorem in [8] to get the solutions of initial value problem for the following system in Y:
is locally Lipschitz continuous. Thus we apply the existence theorem in [8] to get the solutions of initial value problem for the following system in Y:
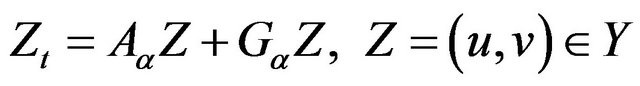 (2.3)
(2.3)
when
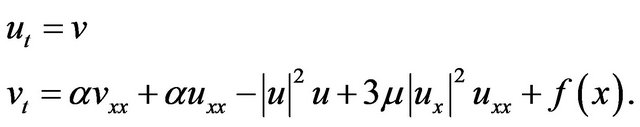 (2.4)
(2.4)
Now, we have the following theorem.
Theorem 2 (Local existence) For 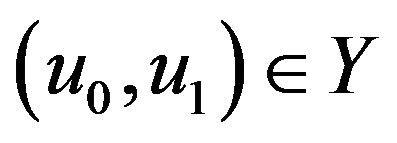 and
and 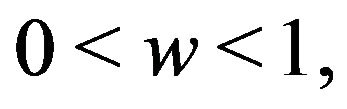 there exists
there exists  such that
such that 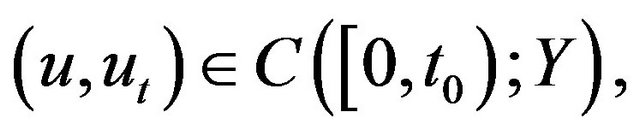
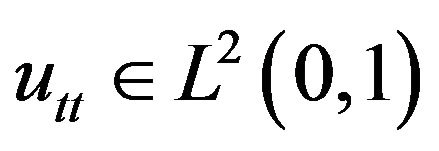 and
and 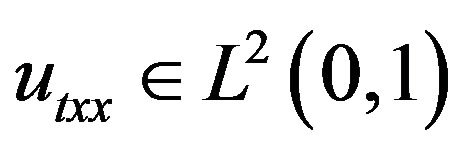 for a.e.
for a.e. 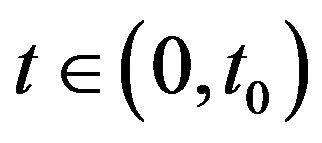 and u satisfies (1.1)-(1.3). Moreover, if
and u satisfies (1.1)-(1.3). Moreover, if ![]() is maximal, then either
is maximal, then either 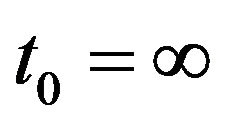 or
or 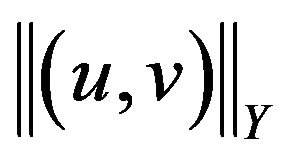 is unbounded on
is unbounded on 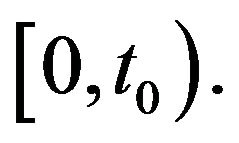
Now for the proof of the Theorem 4 (Global Existence) we give the following Lemma 3. In the proofs of Lemma 3 and Theorem 4 (Global Existence) we repeat a similar technique used in [1].
Lemma 3 For 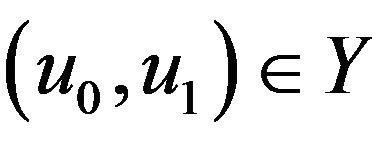 and
and 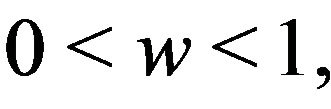 there exist constants
there exist constants 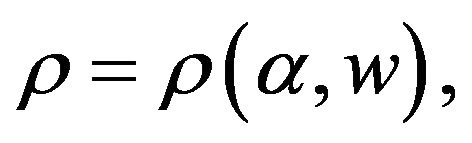
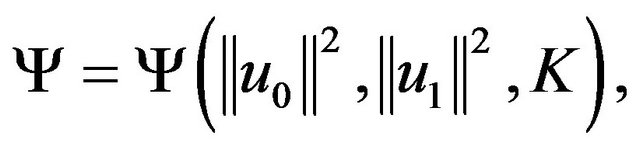
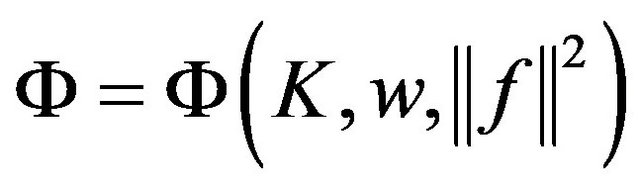 such that for
such that for 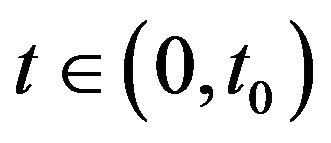
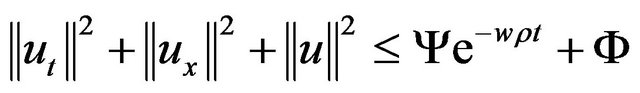 (2.5)
(2.5)
where u is the solution of (1.1)-(1.3).
Proof. Let 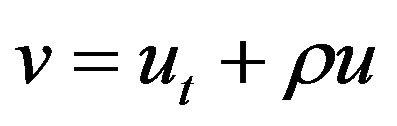 where
where  is a constant to be determined. Thus (1.1) becomes
is a constant to be determined. Thus (1.1) becomes
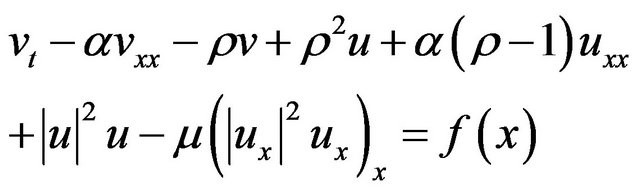 (2.6)
(2.6)
Taking the inner product of both sides of (2.6) with v and integrating the resulting equation, we have
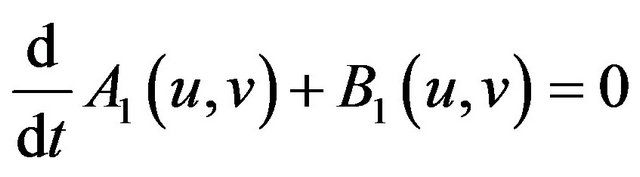 (2.7)
(2.7)
where
 (2.8)
(2.8)
and
 (2.9)
(2.9)
Now we will estimate 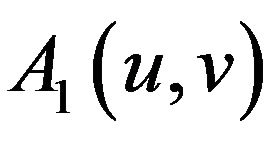 and
and 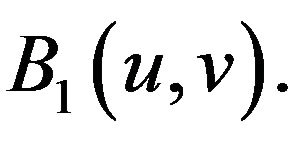 Choose
Choose  such that
such that
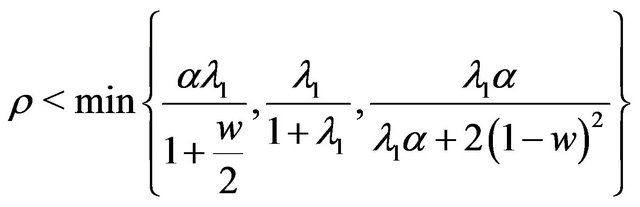 (2.10)
(2.10)
where 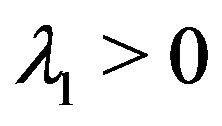 is first eigenvalue of the following problem
is first eigenvalue of the following problem
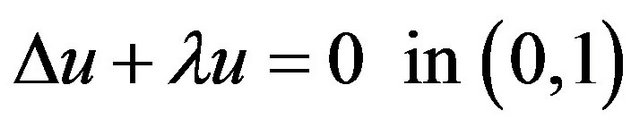
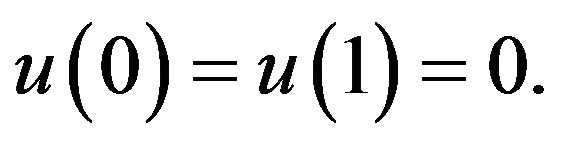
From (2.8) and (2.9) with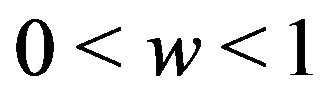 , we get
, we get
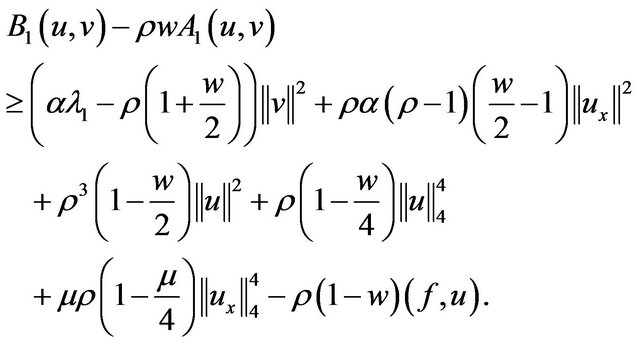 (2.11)
(2.11)
We use Young inequality, Poincaré inequality and (2.10) in (2.11) we find
 (2.12)
(2.12)
Similarly, we obtain
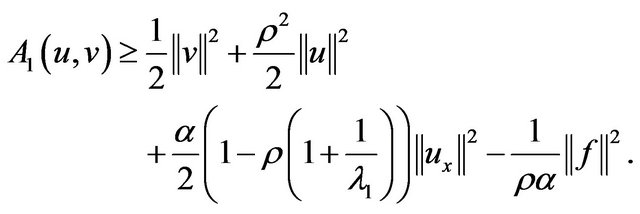 (2.13)
(2.13)
Then (2.7), (2.12) and (2.13) yield
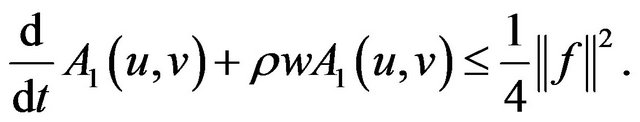 (2.14)
(2.14)
Using Gronwall’s inequality, we have
 (2.15)
(2.15)
Since 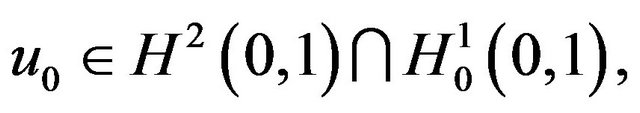 we can find that
we can find that
 by using the Sobolev embedding theorem. Thus using (2.13) in (2.15) we obtain
by using the Sobolev embedding theorem. Thus using (2.13) in (2.15) we obtain
 (2.16)
(2.16)
Taking
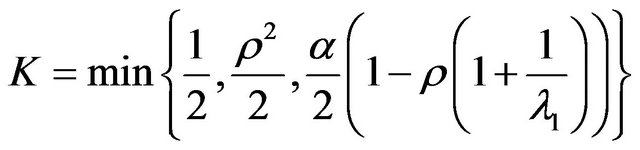
and choosing  we get (2.5).■
we get (2.5).■
Now we can prove the global existence of the problems (1.1)-(1.3).
Theorem 4 (Global Existence) For 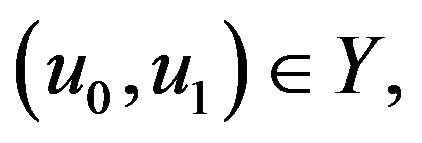 there exists a global solution u of problems (1.1)-(1.3) satisfying
there exists a global solution u of problems (1.1)-(1.3) satisfying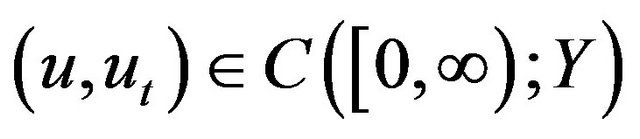 .
.
Proof. In Theorem 2 (Local Existence) we know that  for
for  and
and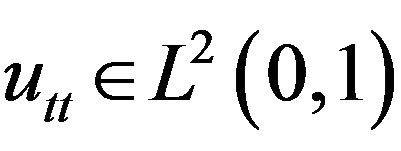 ,
,  for a.e.
for a.e. 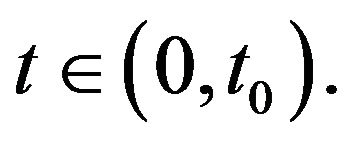 In Lemma 3 we find that
In Lemma 3 we find that 
 and
and  are uniformly bounded for all
are uniformly bounded for all 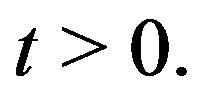 Now we prove the global existence of the solution u. To do this we need to show that
Now we prove the global existence of the solution u. To do this we need to show that 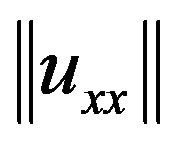 is uniformly bounded for
is uniformly bounded for 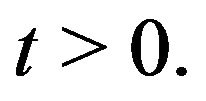
Now, taking the inner product of both sides (1.1) in  with
with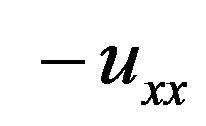 , we have
, we have
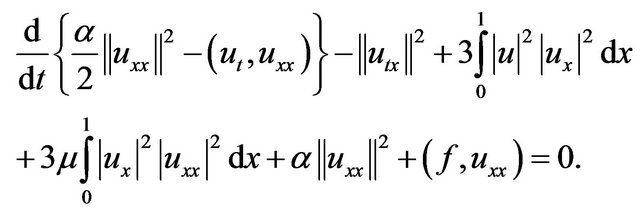 (2.17)
(2.17)
Then we multiply both sides of (2.17) by ![]() and add to (2.7) to obtain
and add to (2.7) to obtain
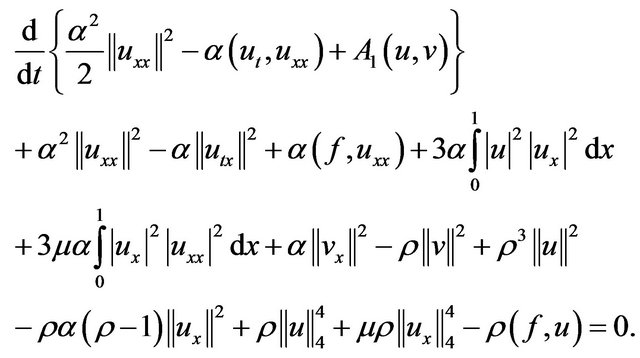 (2.18)
(2.18)
Using Poincaré inequality and (2.10) in (2.18), we have
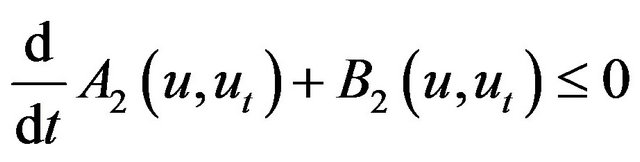 (2.19)
(2.19)
where
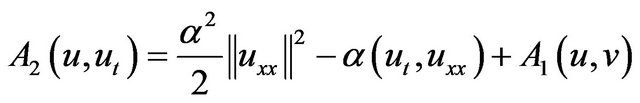 (2.20)
(2.20)
and
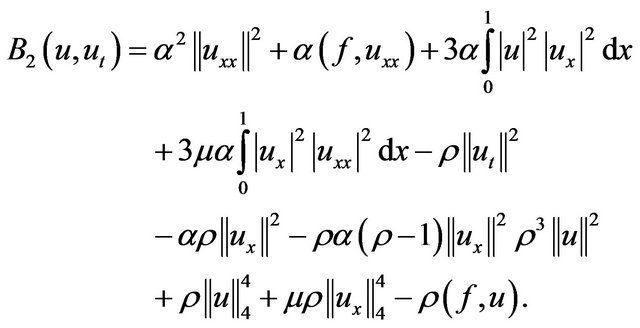 (2.21)
(2.21)
Then thanks to Young inequality we obtain
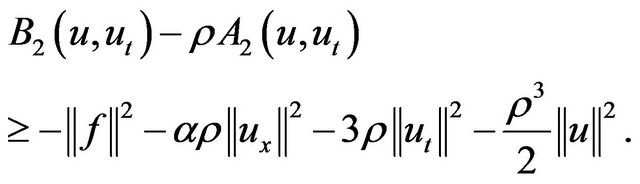 (2.22)
(2.22)
Taking 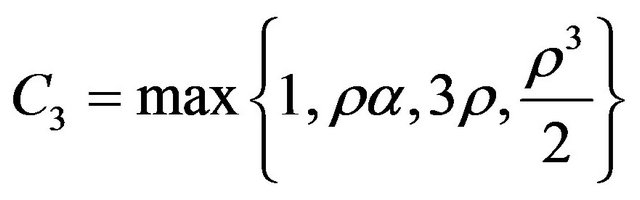 in (2.22) we get
in (2.22) we get
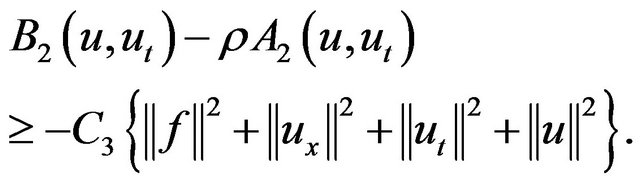 (2.23)
(2.23)
Using (2.19), (2.23) and Gronwall’s inequality we get
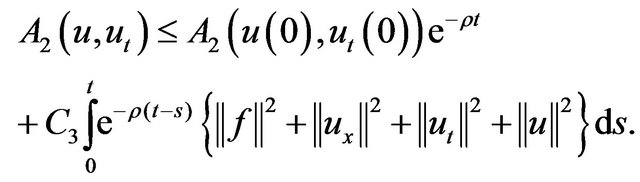 (2.24)
(2.24)
Thus (2.24) and Lemma 3 imply that 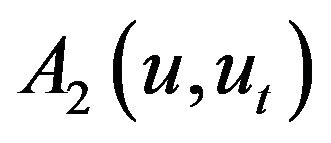 is uniformly bounded in
is uniformly bounded in  because of
because of
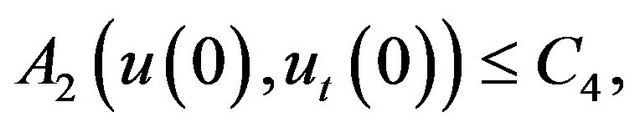 for some constant
for some constant
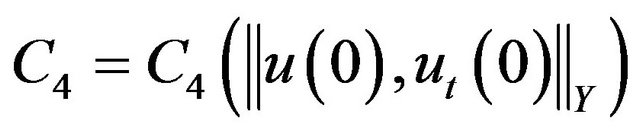 and we have
and we have
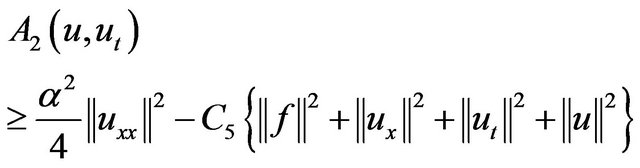 (2.25)
(2.25)
where 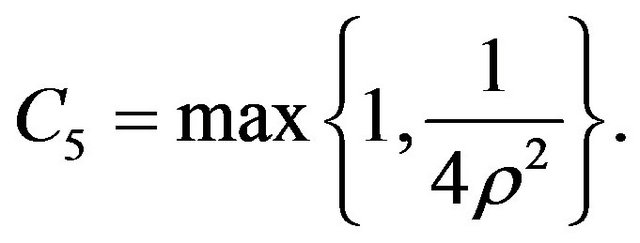 Finally, using Sobolev embedding theorem and Lemma 3 we obtain that
Finally, using Sobolev embedding theorem and Lemma 3 we obtain that 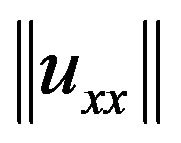 is uniformly bounded in
is uniformly bounded in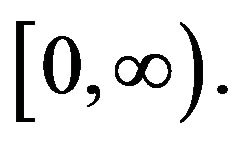 ■
■
Theorem 5 (Uniqueness of weak solution) A weak solution of (1.1)-(1.3) is unique.
Proof. Let u and v be two distinct solutions to (1.1)- (1.3) for the same initial and boundary data. We define the difference of these solutions as ![]() Then from (1.1)-(1.3), w satisfies
Then from (1.1)-(1.3), w satisfies
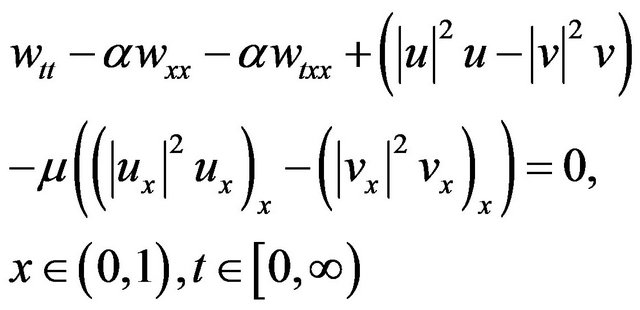 (2.26)
(2.26)
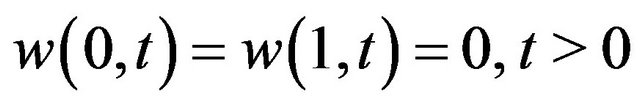 (2.27)
(2.27)
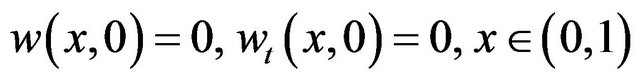 (2.28)
(2.28)
Taking the inner product of (2.26) by 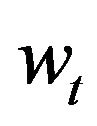 in
in 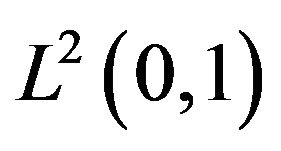 and integrating by parts gives
and integrating by parts gives
 (2.29)
(2.29)
By means of the inequality
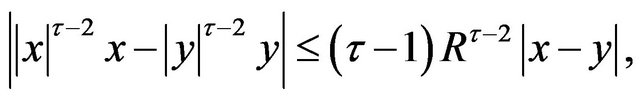 (2.30)
(2.30)
which holds for all 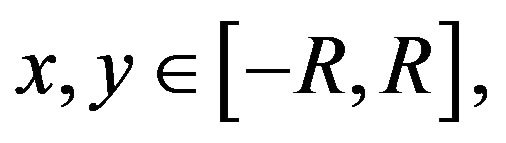
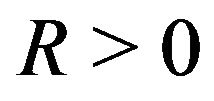 and
and 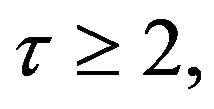 it follows from (2.29) that
it follows from (2.29) that
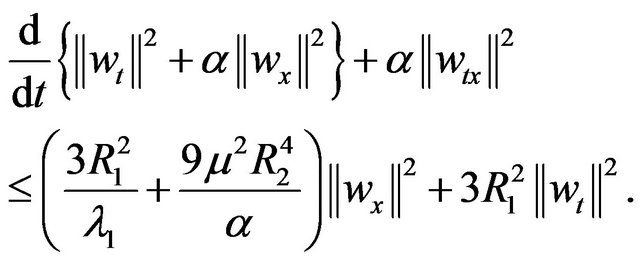 (2.31)
(2.31)
Thus we get
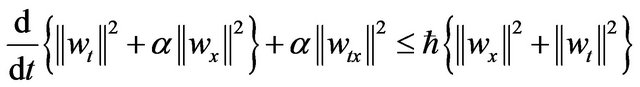 (2.32)
(2.32)
where  Consequently the differential form of Gronwall’s inequality implies to give
Consequently the differential form of Gronwall’s inequality implies to give 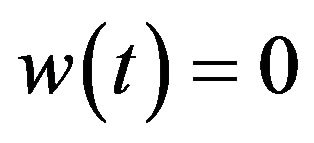 on
on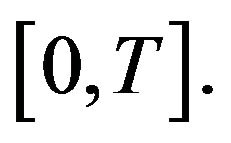 ■
■
3. Existence of Determining Functionals
Now we give some definitions, theorems and corollary for proving existence of determining functionals.
Definition 6 [4] Let 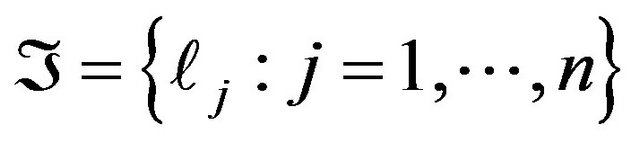 be a finite set of linear continuous functionals on
be a finite set of linear continuous functionals on
 We will say that
We will say that ![]() is a set of determining functionals for (1.1)-(1.3) when for any two solutions
is a set of determining functionals for (1.1)-(1.3) when for any two solutions 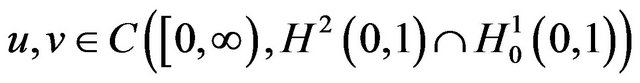 with
with 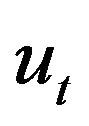
and 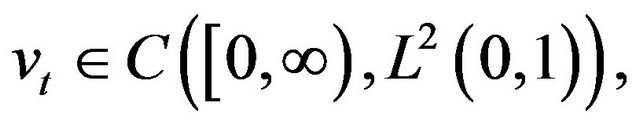 the conditions
the conditions
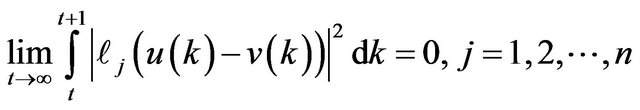 (3.1)
(3.1)
imply
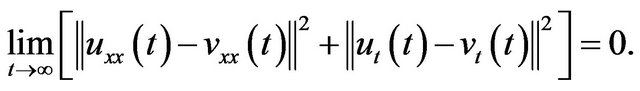 (3.2)
(3.2)
Definition 7 [4] Let V and H be the reflexive Banach spaces and V be continuously and densely embedded into H. Let 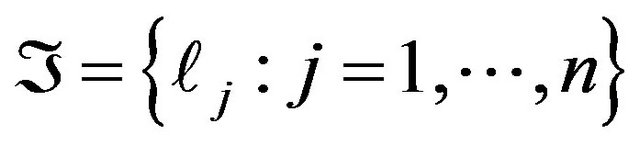 be a set of linear functionals on V. We define the completeness defect
be a set of linear functionals on V. We define the completeness defect 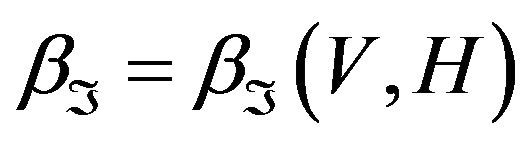 of the set
of the set ![]() with respect to the pair of the spaces V and H by the formula
with respect to the pair of the spaces V and H by the formula
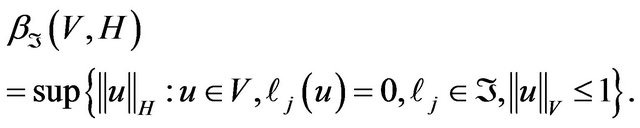 (3.3)
(3.3)
The following assertion gives the spectral characterization of the completeness defect in the case when V and H are the Hilbert spaces.
Theorem 8 [4] Let V and H be the separable Hilbert spaces such that V is compactly and densely embedded into H. Let K be the self-adjoint, positive and compact operator in the space V defined by the equality
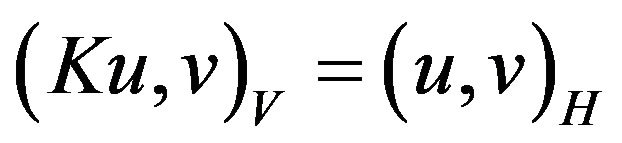
for  Then the completeness defect
Then the completeness defect 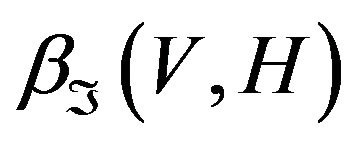 of a set
of a set ![]() of linear functionals on V can be evaluated by the formula
of linear functionals on V can be evaluated by the formula
![]()
where 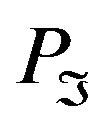 is the orthoprojector in the space V on the annihilator
is the orthoprojector in the space V on the annihilator
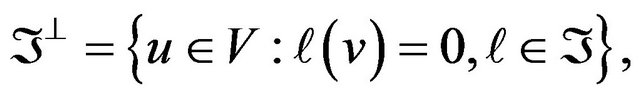
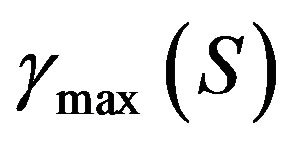 is the maximal eigenvalue of the operator S.
is the maximal eigenvalue of the operator S.
Corollary 9 [4] Let the conditions of Theorem 8 be hold and let us denote by  the orthonormal basis in the space V that consists of the eigenvectors of the operator K:
the orthonormal basis in the space V that consists of the eigenvectors of the operator K:
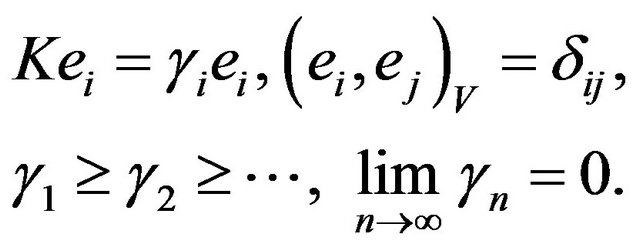 (3.4)
(3.4)
Then the completeness defect of the set of functionals,
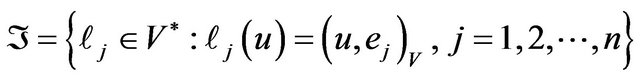
can be evaluated by the formula
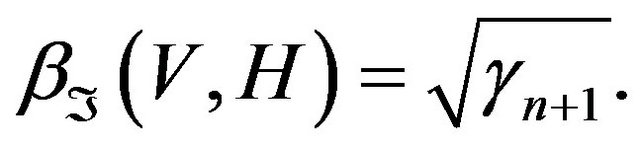
The following theorem establishes a relation between the completeness defect and the set 
Theorem 10 [4] Let  be the completeness defect of a set
be the completeness defect of a set ![]() of linear functionals on V with respect to H. Then there exists a positive constant
of linear functionals on V with respect to H. Then there exists a positive constant 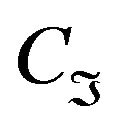 such that
such that
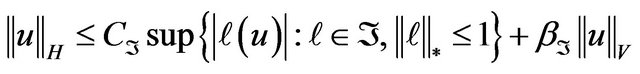 (3.5)
(3.5)
for any  where
where ![]() is the closed linear span of the set
is the closed linear span of the set ![]() in
in  the dual space of V and
the dual space of V and 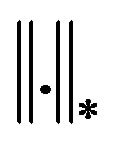 is the norm in
is the norm in 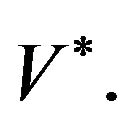
The following version of Gronwall’s lemma is also needed to determine behavior of solutions as 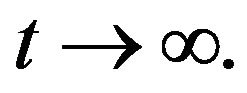
Lemma 11 [4] Let ![]() be a locally integrable real valued function on
be a locally integrable real valued function on  satisfying for some
satisfying for some
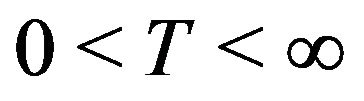 the following conditions
the following conditions
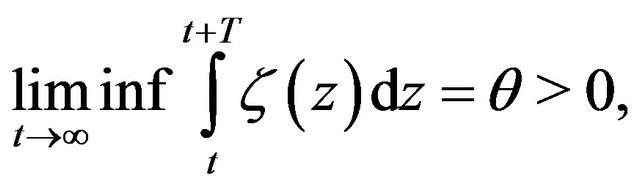 (3.6)
(3.6)
 (3.7)
(3.7)
where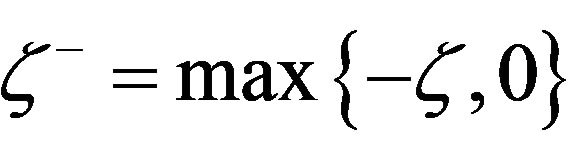 . Further, let κ be a real valued locally integrable function defined on
. Further, let κ be a real valued locally integrable function defined on 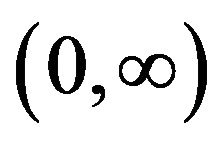 such that
such that
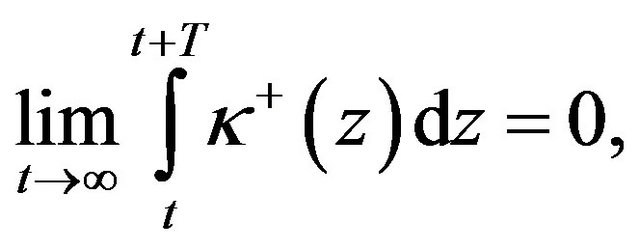 (3.8)
(3.8)
where 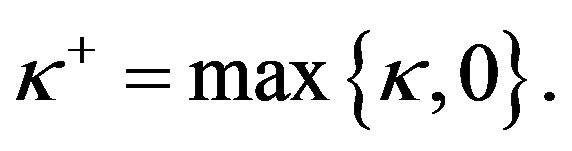 Suppose that
Suppose that ![]() is an absolutely continuous non-negative function on
is an absolutely continuous non-negative function on  such that
such that
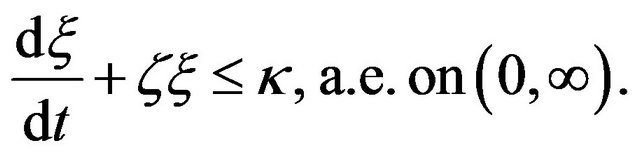 (3.9)
(3.9)
Then  as
as 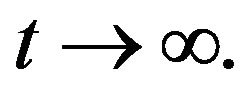
Now we can prove the main result concerning existence of a set of determining functionals of solutions to problems (1.1)-(1.3).
Theorem 12 Let 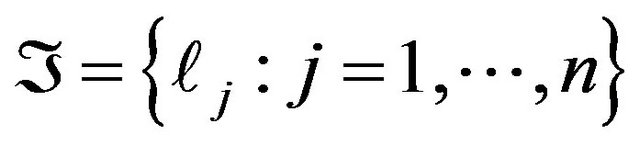 be a set of linear continuous functionals on the space
be a set of linear continuous functionals on the space 
 and let
and let 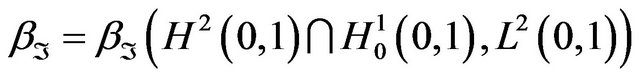 be a positive number satisfying
be a positive number satisfying
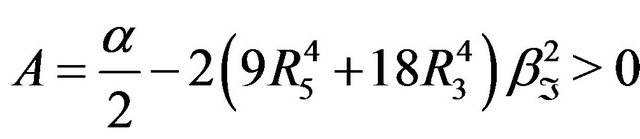 where
where 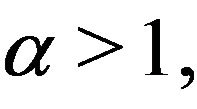 R3, R5 positive constants. Then,
R3, R5 positive constants. Then, ![]() is a set of determining functionals for (1.1)-(1.3).
is a set of determining functionals for (1.1)-(1.3).
Proof. Let u and v be two solutions of problems (1.1)- (1.3). Let ![]() be the difference of these solutions. Thus w satisfies (2.26)-(2.28). Now taking the
be the difference of these solutions. Thus w satisfies (2.26)-(2.28). Now taking the 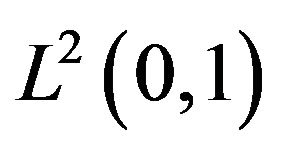 inner product of (2.26) by
inner product of (2.26) by  we get
we get
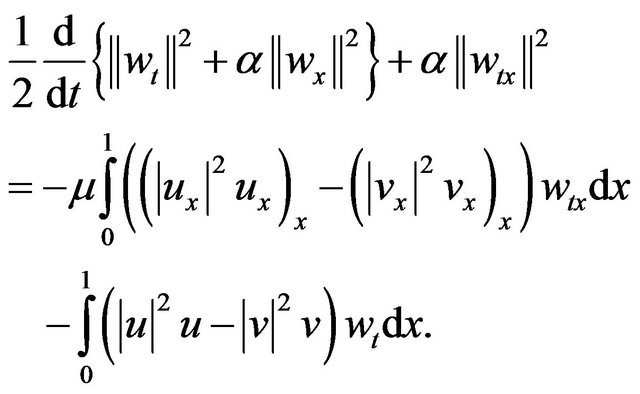 (3.10)
(3.10)
Using (2.30) and Young inequality in right hand side of (3.10) we obtain
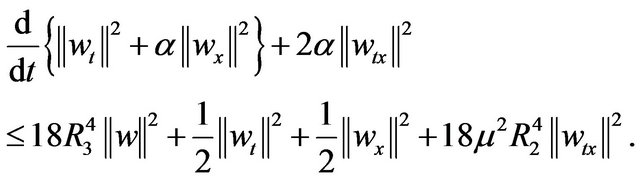 (3.11)
(3.11)
On the other hand, the 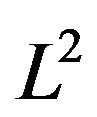 inner product of (2.26) by
inner product of (2.26) by 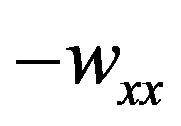 and integration by parts over
and integration by parts over  yields
yields
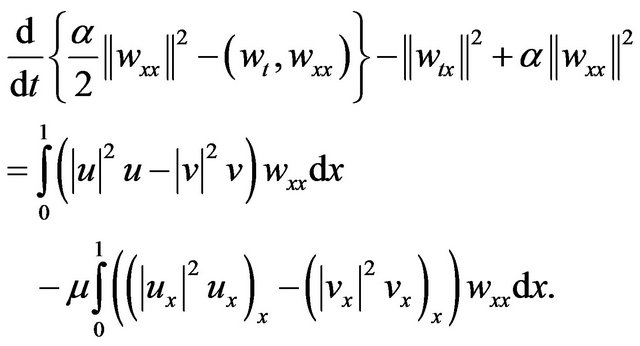 (3.12)
(3.12)
We assume that for some  and any small v, v1,
and any small v, v1, 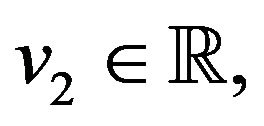 the nonlinear function
the nonlinear function  satisfies
satisfies
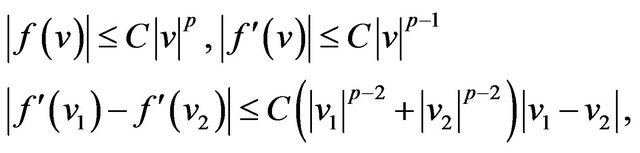 (3.13)
(3.13)
where C is independent of v, v1, v2 [10]. Using (2.30) and (3.13) in (3.12) we have
 (3.14)
(3.14)
Using the Hölder, Young and Sobolev inequalities in right hand side of (3.14) we obtain the estimate
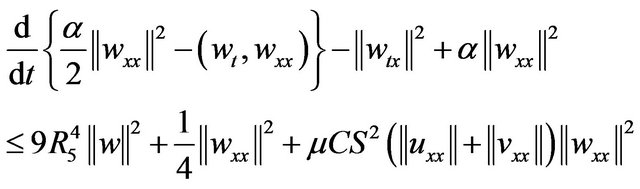 (3.15)
(3.15)
where ![]() is the constant in the Sobolev inequality. Since
is the constant in the Sobolev inequality. Since  there exists a positive constant D such that
there exists a positive constant D such that  Then we get
Then we get
 (3.16)
(3.16)
Adding (3.16) to (3.11) and using Poincaré inequality we obtain
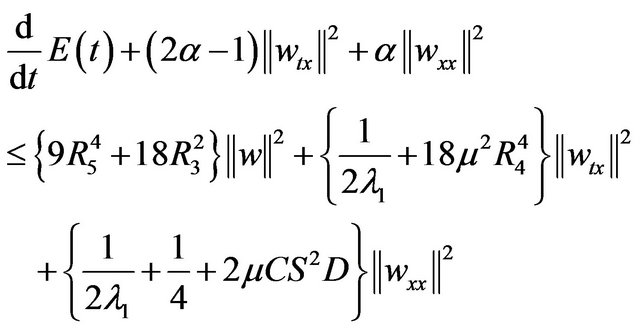 (3.17)
(3.17)
where 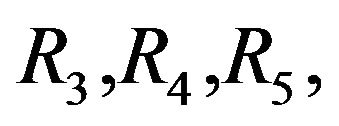 are positive constants and
are positive constants and
 .
.
Choosing
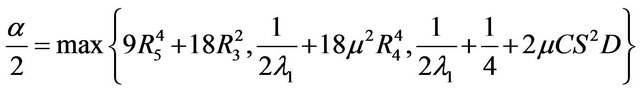
in (3.17) leads to
 (3.18)
(3.18)
Let 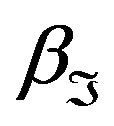 denote the completeness defect between
denote the completeness defect between 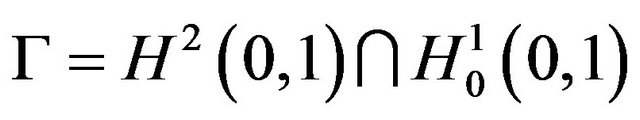 and
and 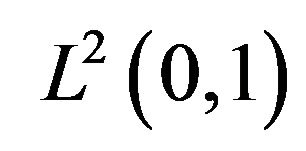 and that is
and that is
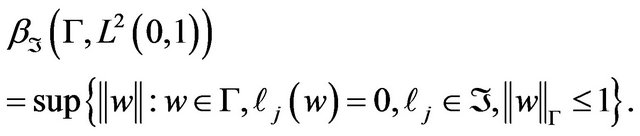 (3.19)
(3.19)
From Theorem 10 we have
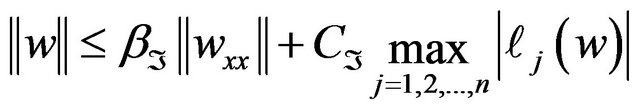 (3.20)
(3.20)
for all 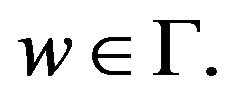 Squaring both sides of (3.20) and using Cauchy’s inequality we obtain
Squaring both sides of (3.20) and using Cauchy’s inequality we obtain
 (3.21)
(3.21)
Combining (3.21) in (3.18) leads to
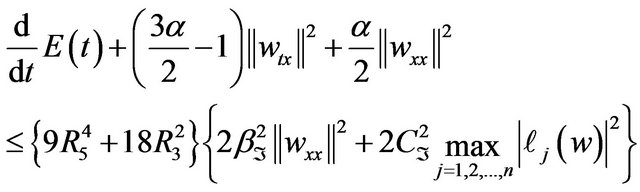 (3.22)
(3.22)
Then we choose 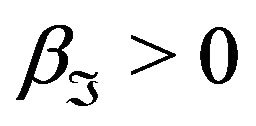 as small as possible so that
as small as possible so that
 Hence, from (3.22) we have
Hence, from (3.22) we have
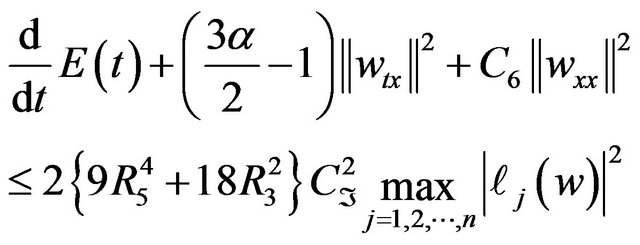 (3.23)
(3.23)
and using Poincaré inequality in (3.23) we find
 (3.24)
(3.24)
Now we find upper and lower bounds for the functional 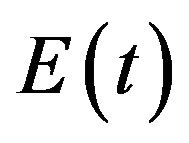 owing to the Cauchy-Schwartz and the Cauchy inequalities:
owing to the Cauchy-Schwartz and the Cauchy inequalities:
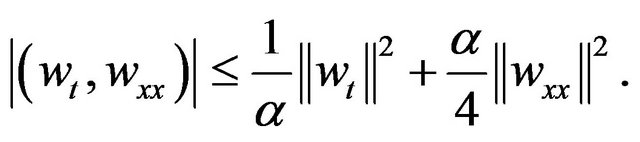 (3.25)
(3.25)
Therefore, using (3.25) and from the definition of , we can find that
, we can find that
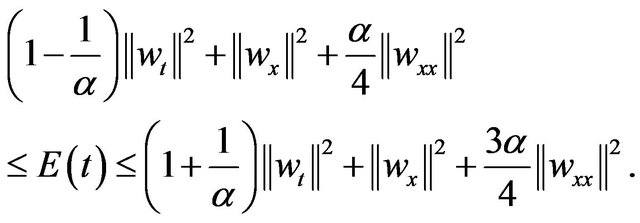 (3.26)
(3.26)
Hence, from (3.26) we can obtain that there exists a positive constant
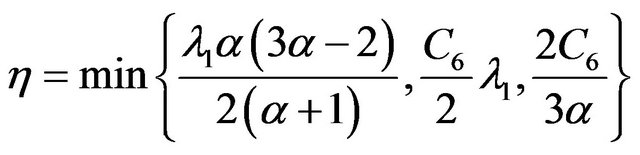
such that
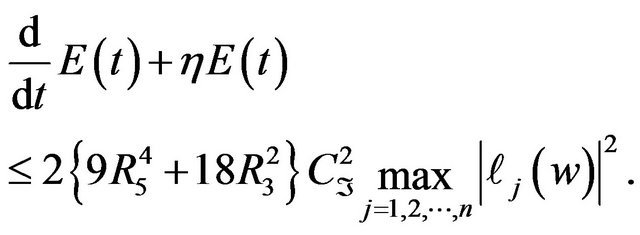 (3.27)
(3.27)
Applying Lemma 11 to (3.27) with
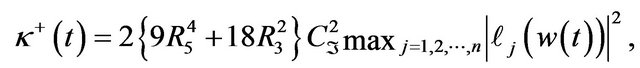
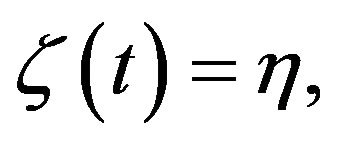 and
and 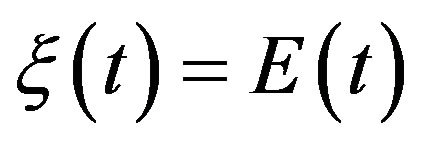 and using a result of Lemma 11 we see that if
and using a result of Lemma 11 we see that if
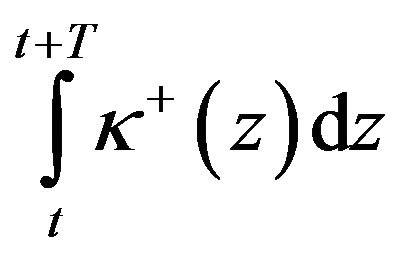
tends to zero as 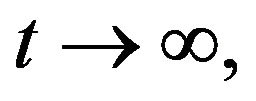 then
then  Thus we obtain that
Thus we obtain that

or
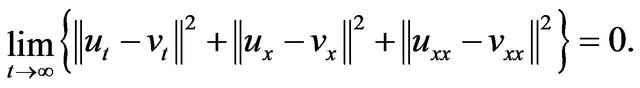
As a result from Definition 6, the set ![]() defined on
defined on ![]() is a set of determining functionals for (1.1)-(1.3). Therefore we complete the proof of Theorem 12.■
is a set of determining functionals for (1.1)-(1.3). Therefore we complete the proof of Theorem 12.■
4. Acknowledgements
The author thanks Professor A. Okay Çelebi for valuable hints and discussions.
REFERENCES
- F. Chen, B. Guo and P. Wang, “Long Time Behavior of Strongly Damped Nonlinear Wave Equations,” Journal of Differential Equations, Vol. 147, No. 2, 1998, pp. 231- 241. doi:10.1006/jdeq.1998.3447
- N. I. Karachalios and N. M. Staurakakis, “Global Existence and Blow up Results for Some Nonlinear Wave Equations on
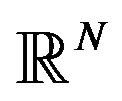 ,” Advances in Differential Equations, Vol. 6, No. 2, 2001, pp. 155-174.
,” Advances in Differential Equations, Vol. 6, No. 2, 2001, pp. 155-174. - A. O. Çelebi and D. Uğurlu, “Determining Functionals for the Strongly Damped Nonlinear Wave Equation,” Journal of Dynamical Systems and Geometric Theories, Vol. 5, No. 2, 2007, pp. 105-116. doi:10.1080/1726037X.2007.10698530
- I. D. Chueshov, “Theory of Functionals That Uniquely Determine Long-Time Dynamics of Infinitive Dimensional Dissipative Systems,” Russian Mathematical Surveys, Vol. 53, No. 4, 1998, pp. 1-58. doi:10.1070/RM1998v053n04ABEH000057
- I. D. Chueshov and V. K. Kalantarov, “Determining Functionals for Nonlinear Damped Wave Equations,” Matematicheskaya Fizika, Analiz, Geometriya, Kharkovskii Matematicheskii Zhurnal, Vol. 8, No. 2, 2001, pp. 215- 227.
- B. Cockburn, D. A. Jones and E. S. Titi, “Determining Degrees of Freedom for Nonlinear Dissipative Systems,” Comptes Rendus de I’Académie des Sciences Paris Série I Mathématique, Vol. 321, 1995, pp. 563-568.
- J. Duan, E. S. Titi and P. Holmes, “Regularity, Approximation and Asymptotic Dynamics for a Generalized Ginzburg-Landou Equation,” Nonlinearty, Vol. 6, No. 6, 1993, pp. 915-933. doi:10.1088/0951-7715/6/6/005
- D. Henry, “Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Mathematics,” Springer-Verlag, New York, 1981.
- P. Massatt, “Limiting Behavior for Strongly Damped Nonlinear Wave Equations,” Journal of Differential Equations, Vol. 48, No. 3, 1983, pp. 334-349. doi:10.1016/0022-0396(83)90098-0
- H. Takeda and S. Yoshikawa, “On the Initial Value Problem of the Semilinear Beam Equation with Weak Damping II: Asymptotic Profiles,” Journal of Differential Equations, Vol. 253, No. 11, 2012, pp. 3061-3080.

