Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24364,4 pages DOI:10.4236/apm.2012.26054
A Note on Nilpotent Operators
Department of Mathematics, Duquesne University, Pittsburgh, USA
Email: gaura@duq.edu
Received July 16, 2012; revised September 11, 2012; accepted September 19, 2012
Keywords: Numerical Range; Numerical Radius; Nilpotent Operator Weighted Shift; Eigenvalues
ABSTRACT
We find that a bounded linear operator T on a complex Hilbert space H satisfies the norm relation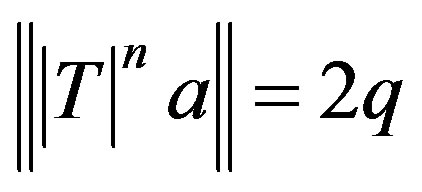 ,
, 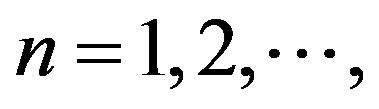 for any vector a in H such that
for any vector a in H such that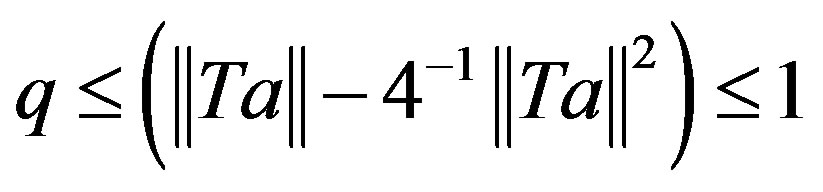 . A partial converse to Theorem 1 by Haagerup and Harpe in [1] is suggested. We establish an upper bound for the numerical radius of nilpotent operators.
. A partial converse to Theorem 1 by Haagerup and Harpe in [1] is suggested. We establish an upper bound for the numerical radius of nilpotent operators.
1. Introduction
The motivation for this note is provided by the results obtained in [1-4]. Let T be a bounded linear operator on a complex Hilbert space H. The numerical range of T, denoted by W(T), is the subset of the complex plane and

The numerical radius of T is defined as,

The following lemma is known and is an easy consequence of the definitions involved.
Lemma 1.1.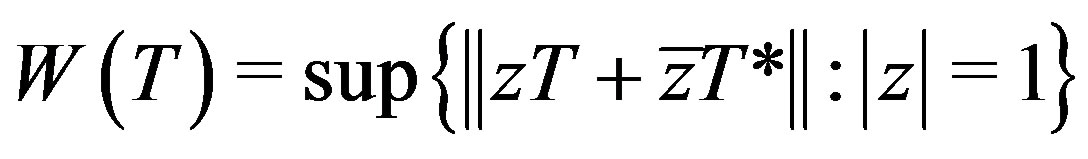 , where T* is the adjoint operator of T and
, where T* is the adjoint operator of T and 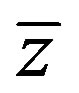 is the complex conjugate of
is the complex conjugate of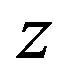 .
.
Berger and Stampfli in [2] have proved that if 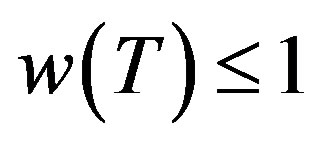 and
and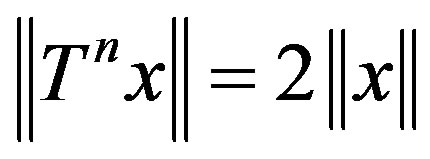 , for some n, then
, for some n, then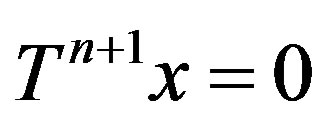 . Also, they gave an example of an operator T and an element
. Also, they gave an example of an operator T and an element  such that
such that 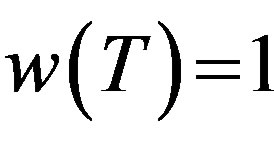 implies that
implies that 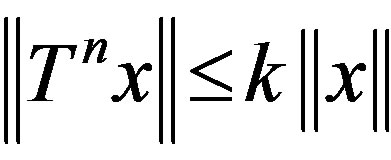 and
and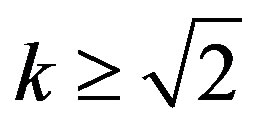 . In Theorem 2.1, we present a different proof of their result in [2] and show that
. In Theorem 2.1, we present a different proof of their result in [2] and show that 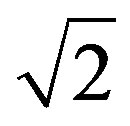 is indeed the best constant.
is indeed the best constant.
Theorem 2.1 also generalizes the result in [4] and provides a partial converse to Theorem 1 in [1, p. 372].
Our next main result in Theorem 2.3 gives an alternative and shorter proof of Theorem 1 in [1].
Applying Lemma 2 and Proposition 2 of [1], a new result on the numerical range of nilpotent operators on H is obtained in Theorem 2.4. This gives a restricted version of Theorem 1 in [3].
Finally, two examples are discussed. Example 3.1 deals with the operator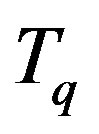 , where 1 is not the eigenvalue of
, where 1 is not the eigenvalue of 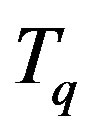 if
if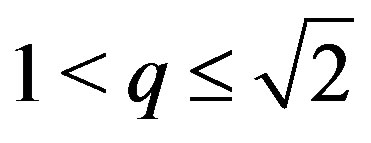 . Example 3.3 justifies why
. Example 3.3 justifies why 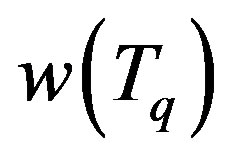 fails to increase until and unless
fails to increase until and unless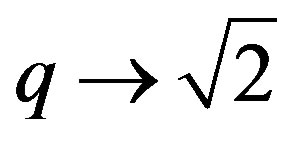 .
.
2. Main Results
Theorem 2.1. The following statements are true for a bounded linear operator T on a Hilbert space H with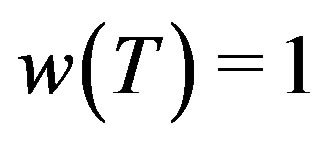 .
.
1) 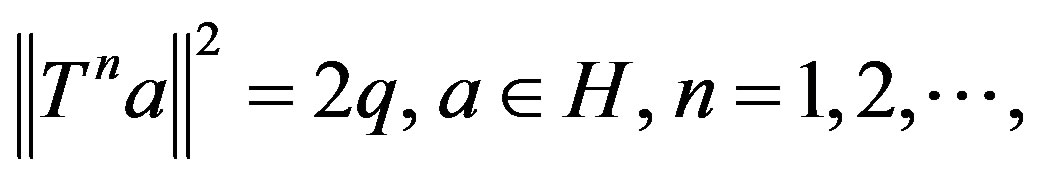 such that
such that
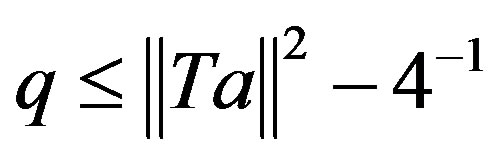 ,
, .
.
2) If 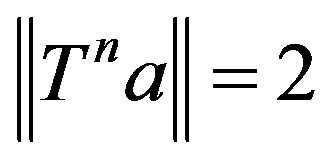 for some integer n, then
for some integer n, then
 and
and .
.
3) The set 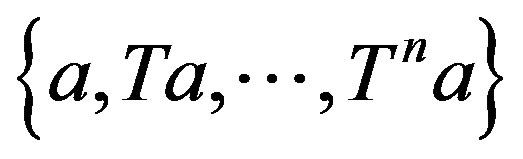 forms a nontrivial subspace of T so that its orthogonal complement is invariant.
forms a nontrivial subspace of T so that its orthogonal complement is invariant.
Proof. 1) For each real number  and a postive integer, n, let
and a postive integer, n, let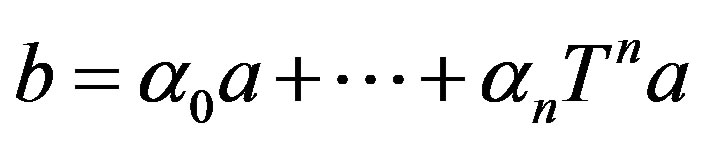 . Then the inner product relation
. Then the inner product relation 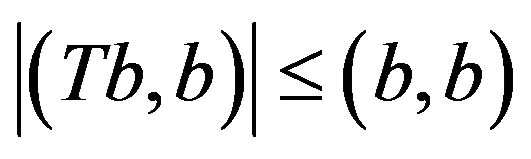 implies that
implies that

That is,
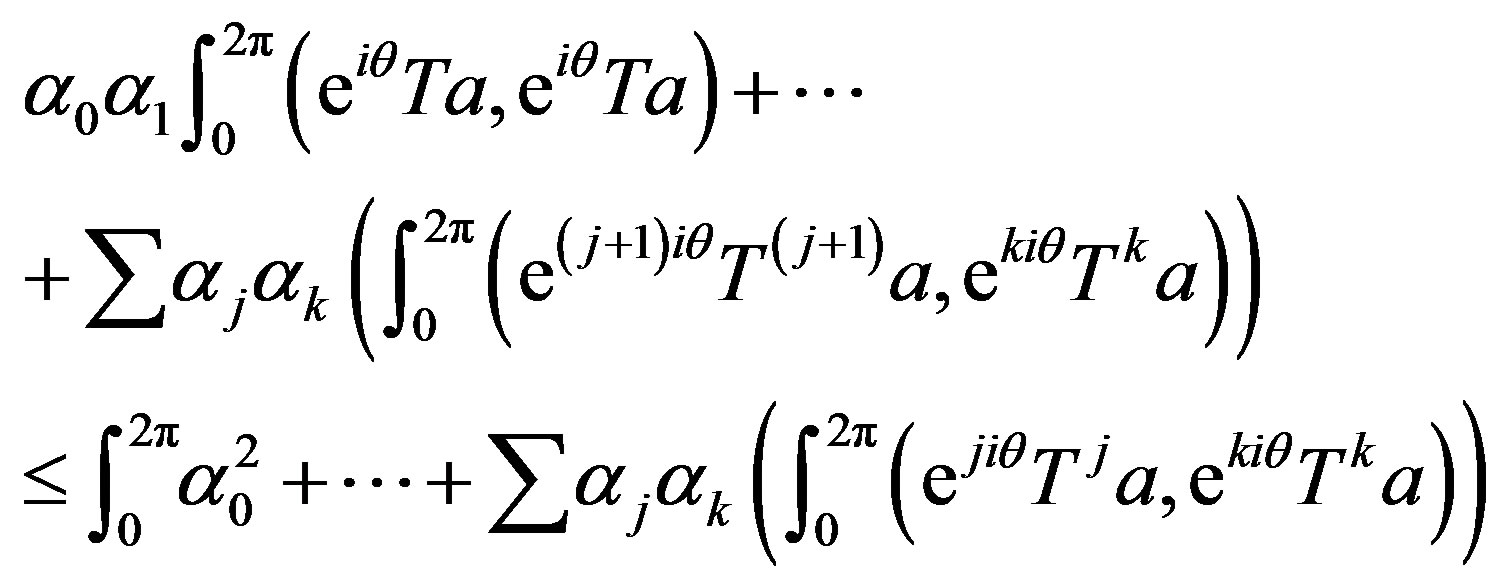
Hence,
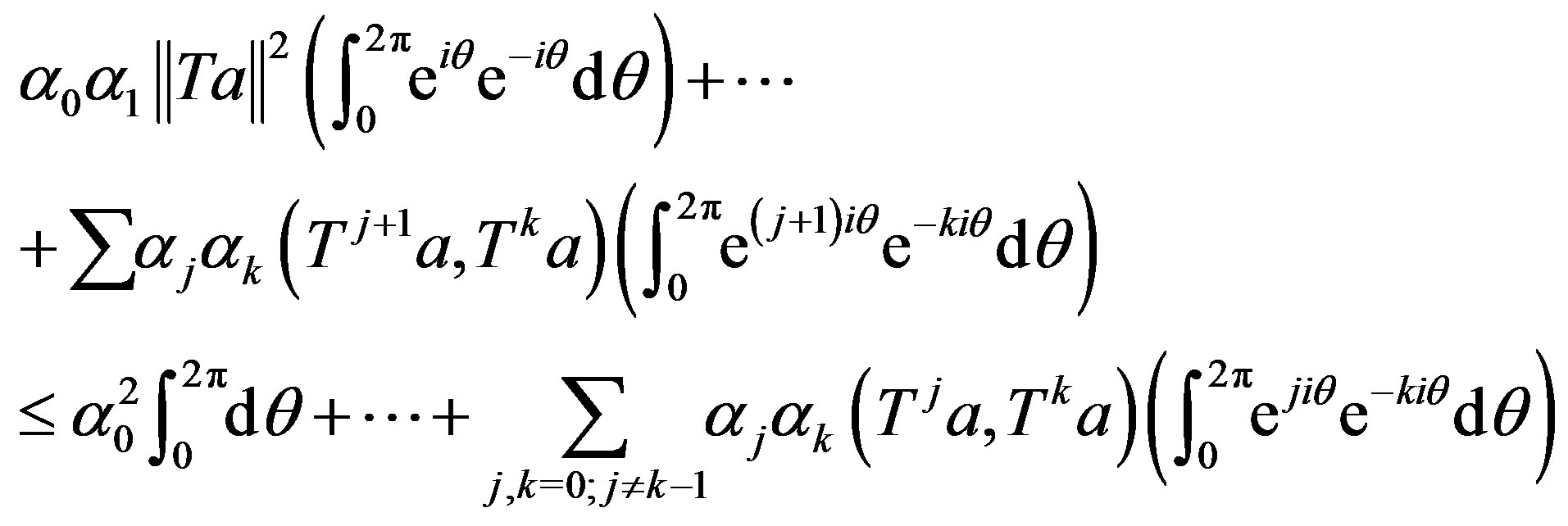
Since
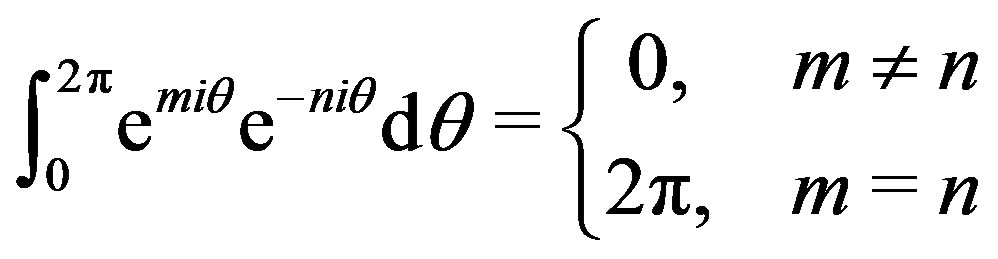
it follows that
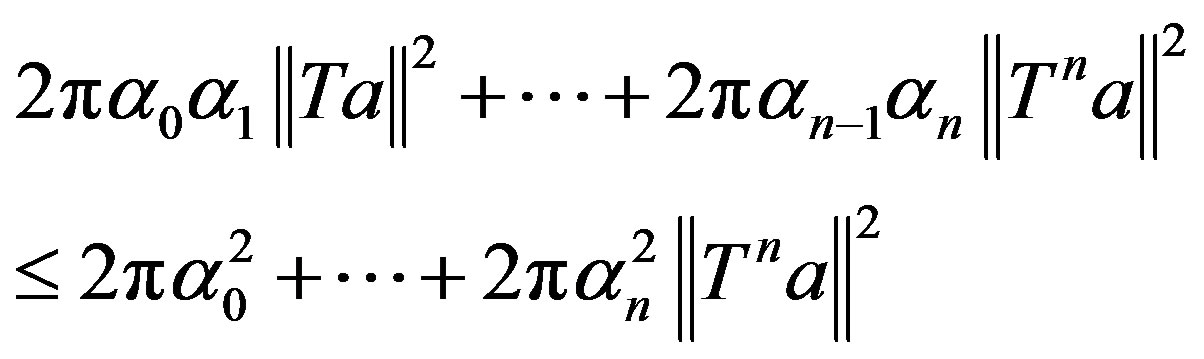
Dividing the above inequality by , we have
, we have

Let  be the following block-diagonal matix of order n and
be the following block-diagonal matix of order n and
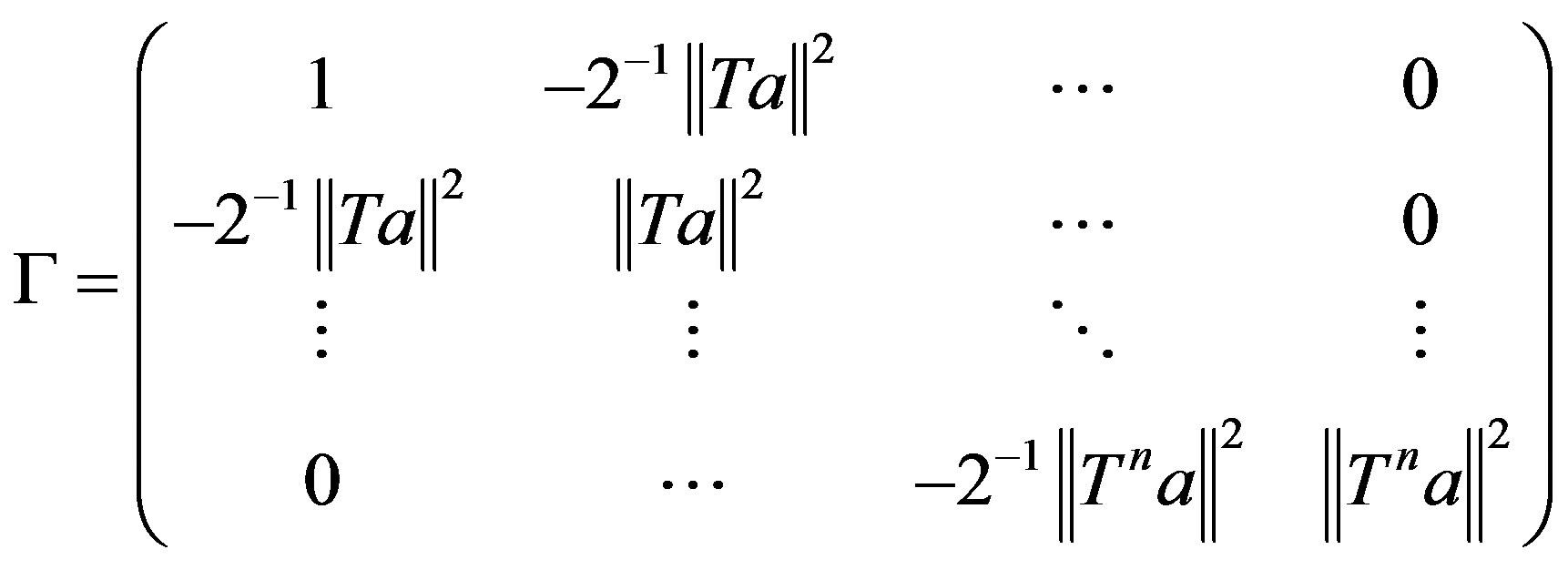
If γn denotes the determinant of  such that
such that 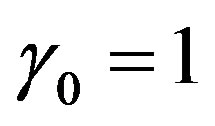 then the value of γn is positive because all principal minors of
then the value of γn is positive because all principal minors of 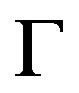 are nonnegative. Suppose that
are nonnegative. Suppose that 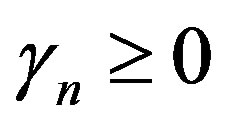
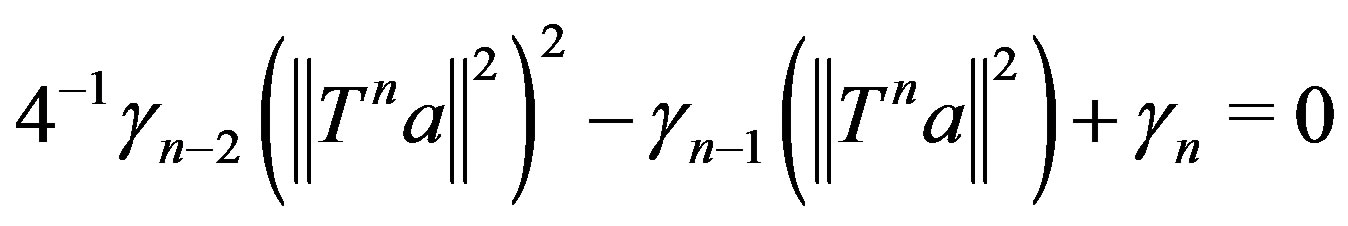 (2.1)
(2.1)
We consider the following cases:
Case 1. If for the least
for the least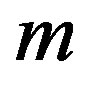 then
then
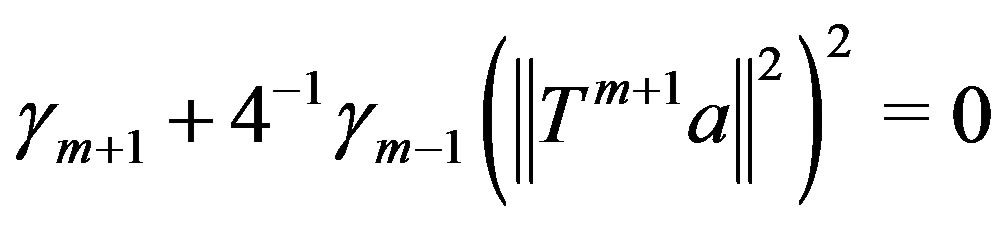 and
and 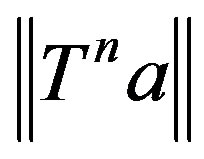 converges to zero.
converges to zero.
Case 2. Let 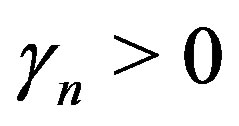 for all
for all . Then
. Then
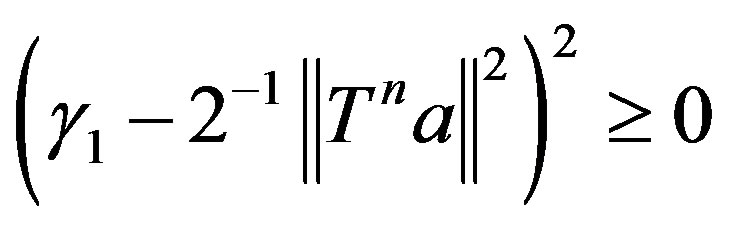 and by induction
and by induction
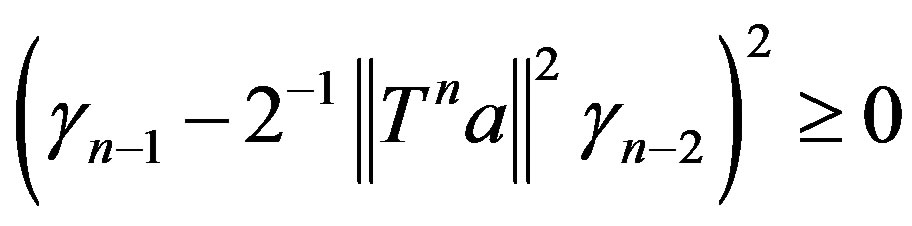
Further, the inequality

implies that 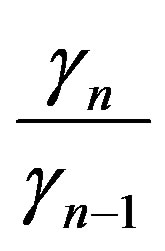 converges to q as n goes to infinity for some q ≥ 0. Therefore from Equation (2.1),
converges to q as n goes to infinity for some q ≥ 0. Therefore from Equation (2.1), 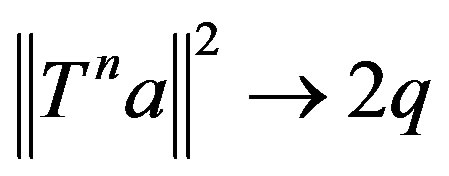 as
as . Thus
. Thus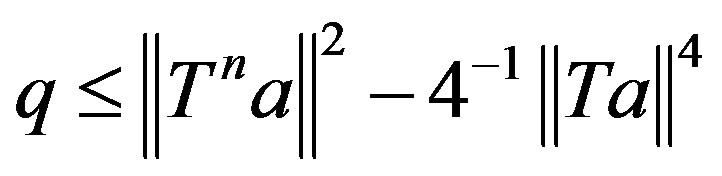 . Obviously, q = 1 only if
. Obviously, q = 1 only if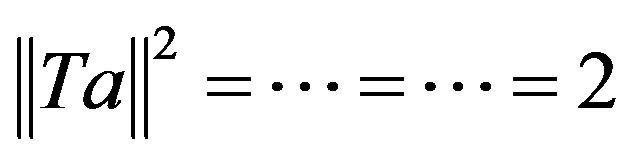 .
.
2) By the assumption,  for some positive integer n. Now fom Equation (2.1), we obtain:
for some positive integer n. Now fom Equation (2.1), we obtain:

and 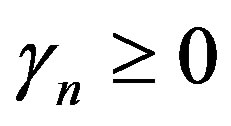 so that
so that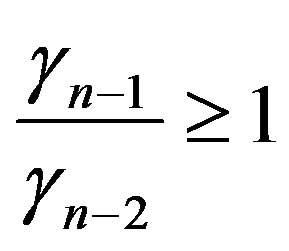 . The equality,
. The equality,
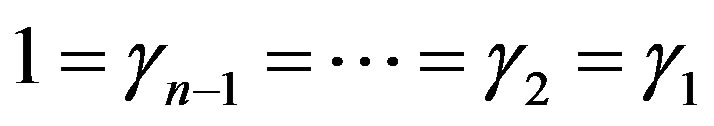 now follows from (a) and thus
now follows from (a) and thus . Also,
. Also, 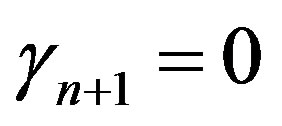 which gives
which gives 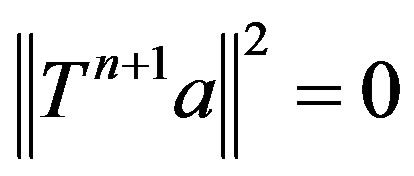 since
since .
.
3) To prove this case, we assume that if the vector 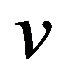 is orthogonal to the spanning set
is orthogonal to the spanning set 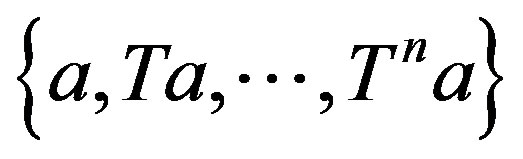 then
then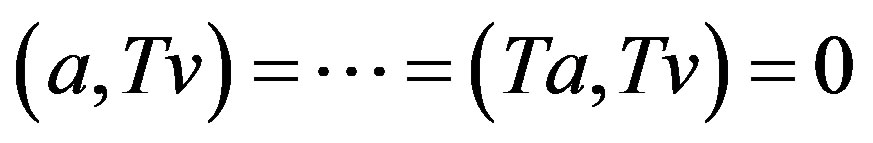 . Let
. Let
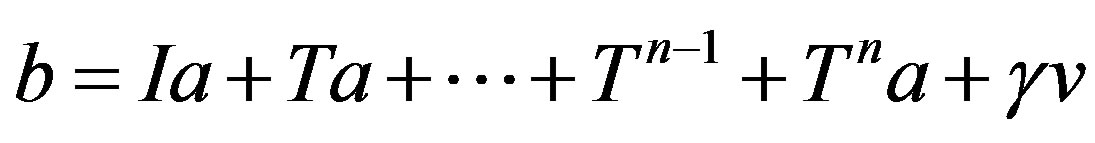 , for
, for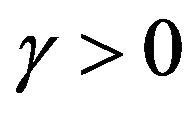 . Then
. Then
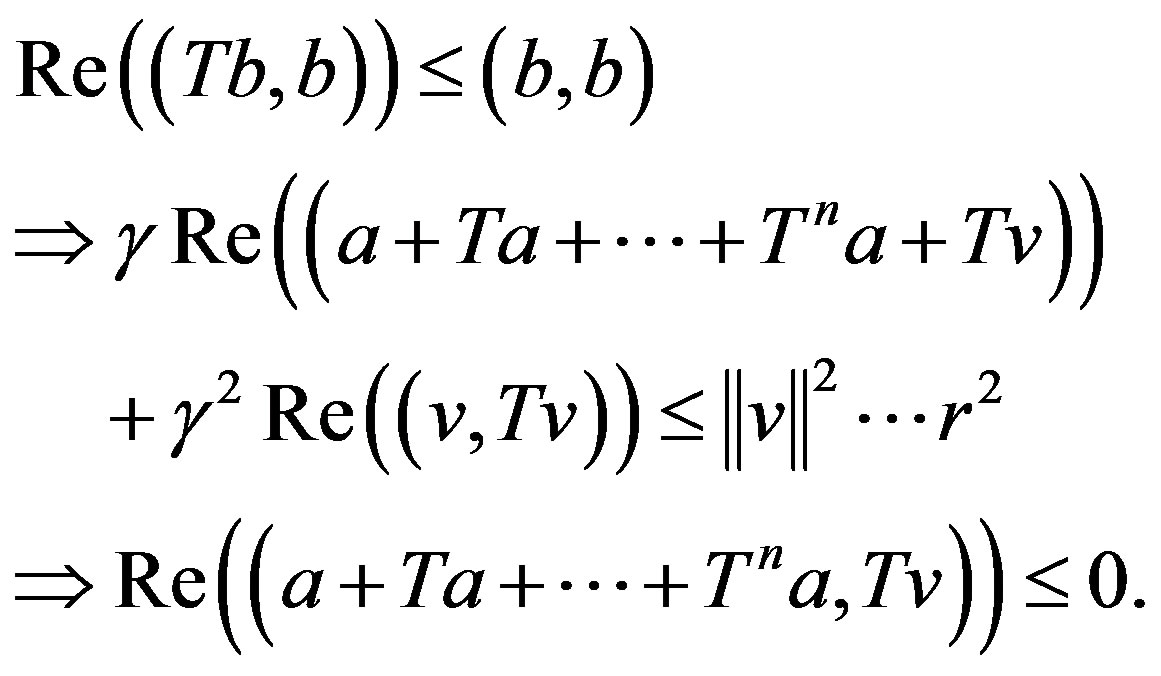
Hence, 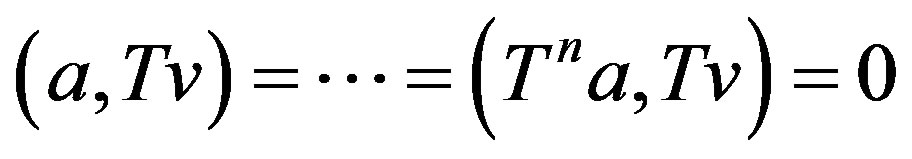 for
for  and the spanning set
and the spanning set 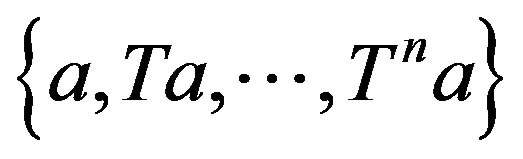 is a non-trivial invariant subspace on T.
is a non-trivial invariant subspace on T.
In [2, p. 1052], an example of an operator T on  and an element x in H with
and an element x in H with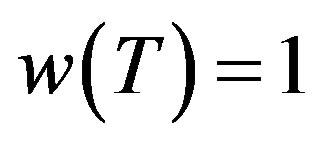 , is given where
, is given where
 . Theorem 2.1 above establishes that
. Theorem 2.1 above establishes that 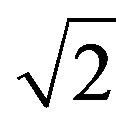 is the best constant in this case.
is the best constant in this case.
Remark 2.2. An operator A on H is hyponormal if
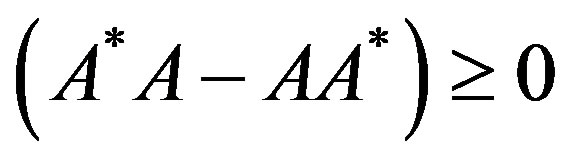 . Let
. Let  then
then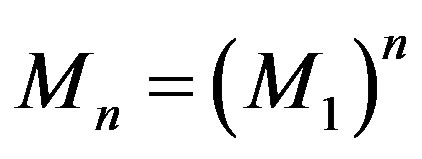 if A is a hyponormal operator. Hence,
if A is a hyponormal operator. Hence,  ,
,  and the set of vectors
and the set of vectors 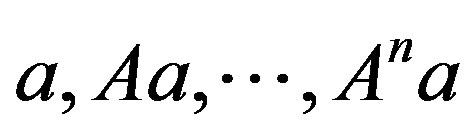 forms a reducing subspace of A.
forms a reducing subspace of A.
A natural connection between Feijer’s inequality and the numerical radius of a nilpotent operator was estaplished by Haagerup and Harpe in [1]. They proved, using positive definite kernals, that for a bounded linear operator T on a Hilbert space H such that 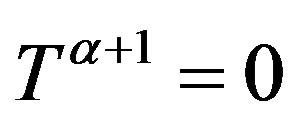 and
and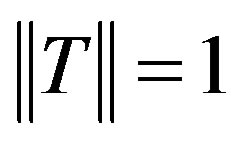 then
then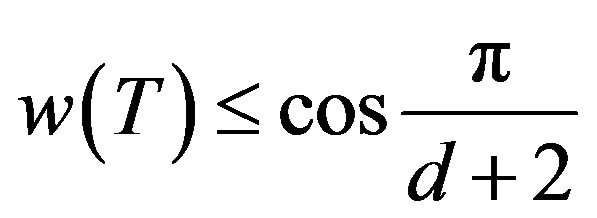 . The external operator is shown to be a truncated shift with a suitable choice of the vector in H. The inequality is related to a result from Feijer about trigonometric polynomials of the form
. The external operator is shown to be a truncated shift with a suitable choice of the vector in H. The inequality is related to a result from Feijer about trigonometric polynomials of the form
 with
with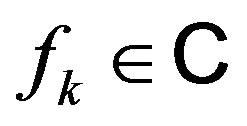 . Such a polynomial is positive if
. Such a polynomial is positive if  for all
for all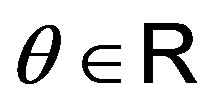 . Here, we present a simplified proof of Theorem 1 in [1].
. Here, we present a simplified proof of Theorem 1 in [1].
Theorem 2.3. For an operator N on H with 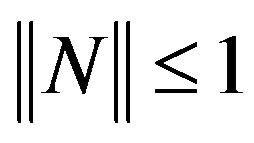 and
and , we have
, we have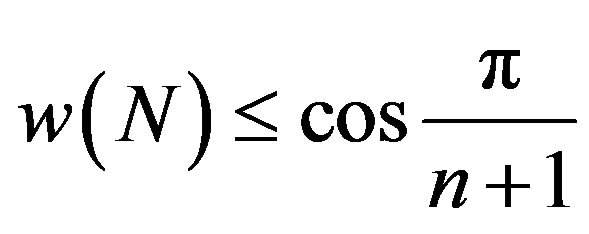 .
.
Proof. We will follow the notations of Theorem 1 in [1]. Let S be the operator on 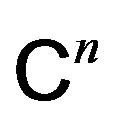 and
and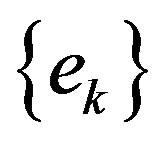 ,
, 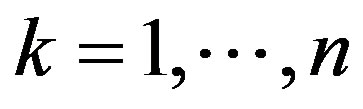 be the basis in
be the basis in . We define the operator S as follows:
. We define the operator S as follows:
 and
and 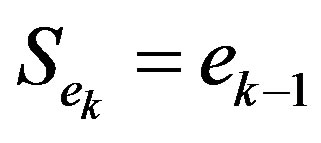 for
for 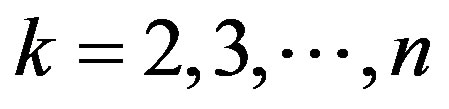
The matrix for S gives a dialation for T. Let A be the matrix for S and
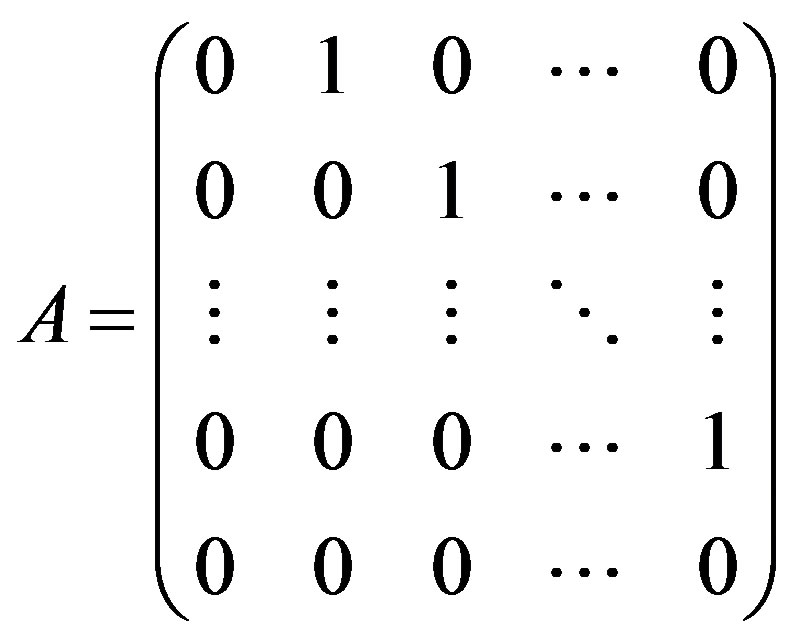
If  is a unitary operator on
is a unitary operator on  with diagonal
with diagonal  then
then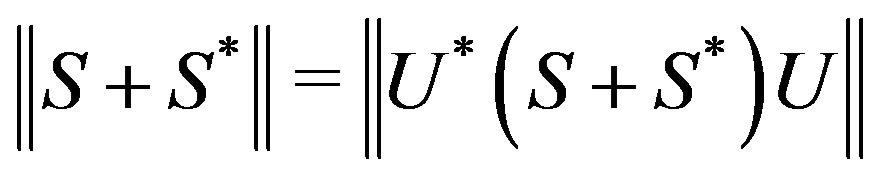 . By Lemma 1, we have:
. By Lemma 1, we have:
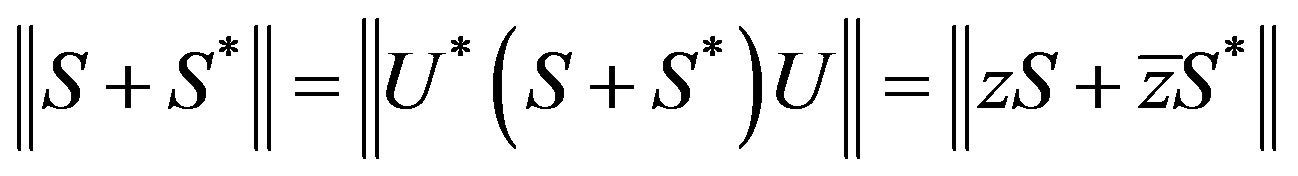
This helps to define the characteristic function of a contraction.
For the operator N on H, let 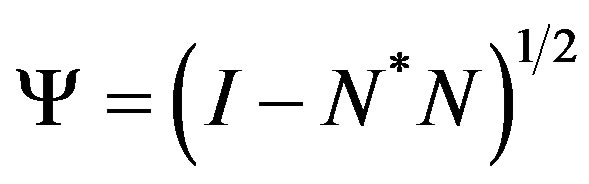 then
then
 is a positive operator and
is a positive operator and  depends on N. Let the range of
depends on N. Let the range of  be denoted by
be denoted by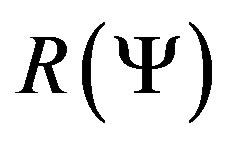 . Then the tensor product,
. Then the tensor product, 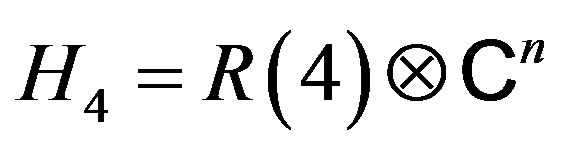 , is a Hilbert space. We define the map
, is a Hilbert space. We define the map 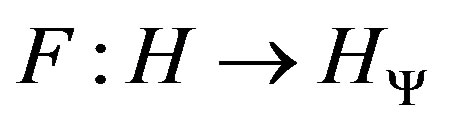 so that F is an isometry.
so that F is an isometry.
For λ, let  where
where 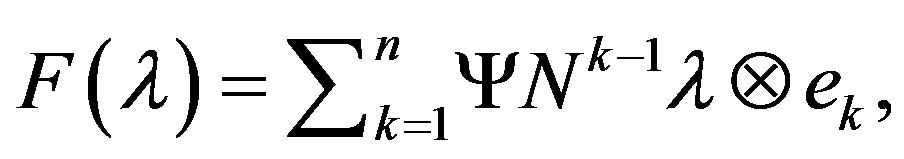 I is the identity operator, and
I is the identity operator, and 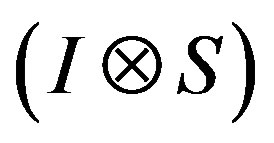 is an operator on
is an operator on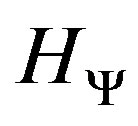 .
.
Therefore  and
and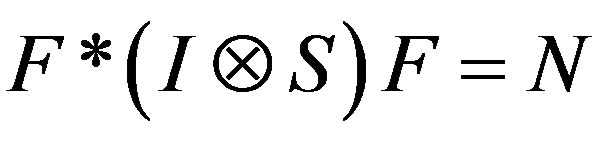 .
.
Now, we claim that , for we hope that
, for we hope that  By Lemma 1.1
By Lemma 1.1
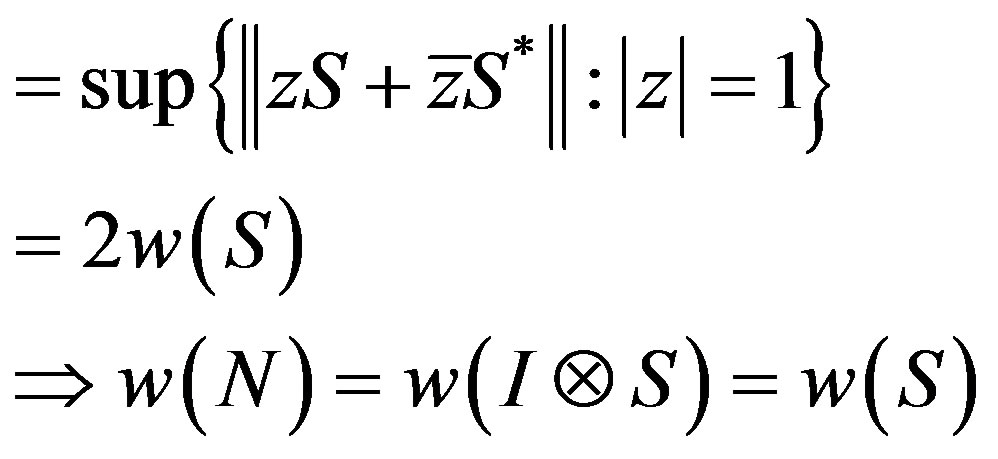
That is,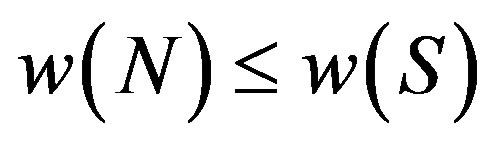 .
.
Since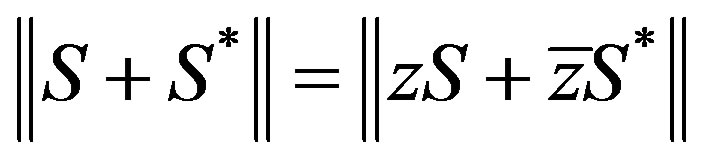 , we have:
, we have:

and

where 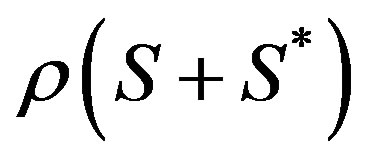 is the spectral radius of
is the spectral radius of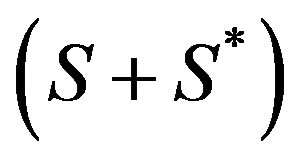 . By the definition of the spectral radius, we have the characteristic polynomial f such that
. By the definition of the spectral radius, we have the characteristic polynomial f such that 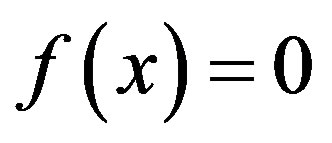 by [5, p. 179, Example 9], the roots of
by [5, p. 179, Example 9], the roots of 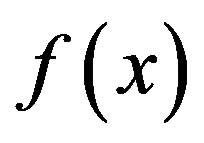 are given by
are given by
 ,
, and
and 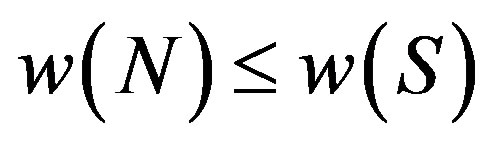 and
and
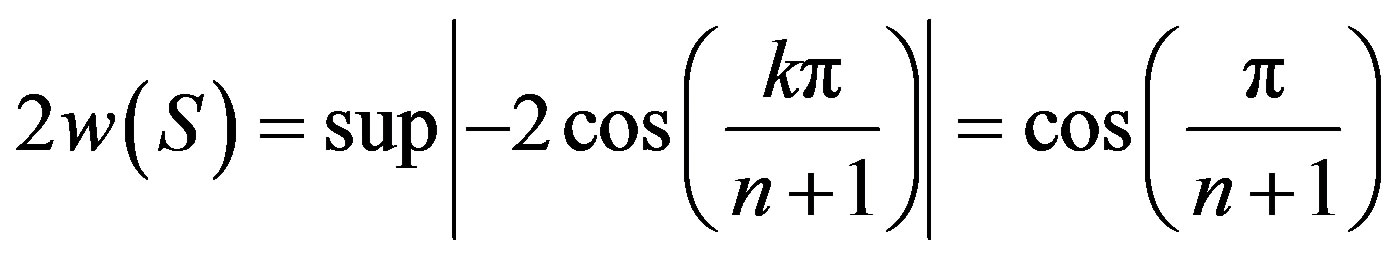 .
.
Karaev in [3] has proved, using Theorem 1 in [1] and the Sz.-Nagy-Foias model in [6] that the numerical range 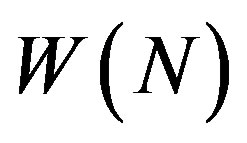 of an arbitrary nilpotent operator N on a complex Hilbert space H is an open or closed disc centered at zero with radius less than or equal to
of an arbitrary nilpotent operator N on a complex Hilbert space H is an open or closed disc centered at zero with radius less than or equal to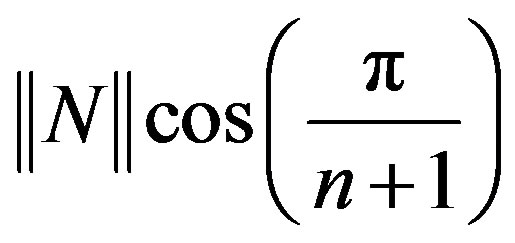 ,
, 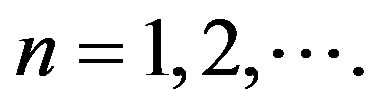
Using Theorem 2 and the assumption that
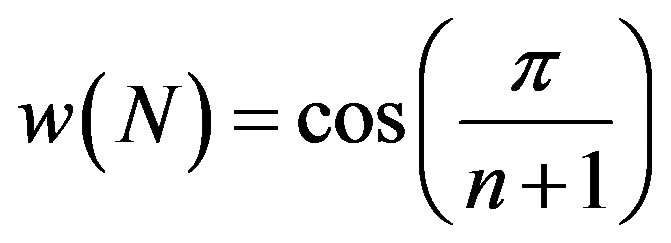 ,
, 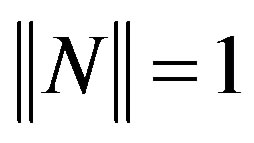 , we have
, we have  as a closed or an open disc centered at zero with radius equal to
as a closed or an open disc centered at zero with radius equal to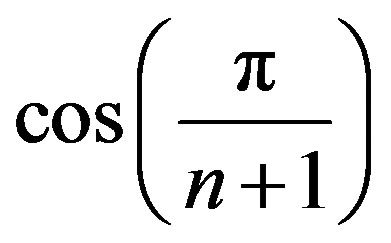 . In fact, we have the following theorem.
. In fact, we have the following theorem.
Theorem 2.4. For a nilpotent operator N on H with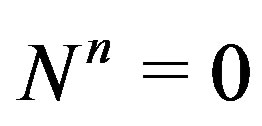 ,
, 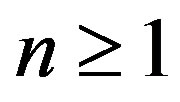 and
and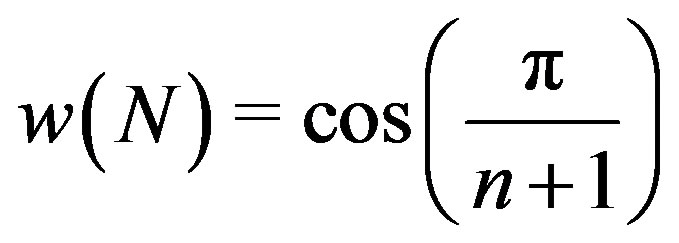 , the numerical range
, the numerical range 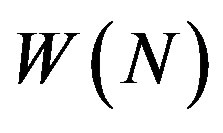 is a disc centered at zero with radius
is a disc centered at zero with radius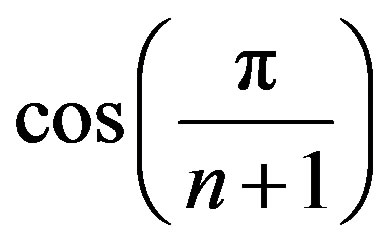 .
.
Proof. For any  we must claim that
we must claim that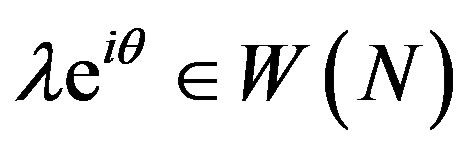 , for
, for 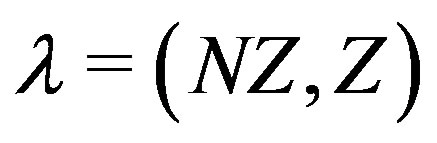 and
and  is a vector in
is a vector in .
.
From [1, p. 374, Proposition 2], we have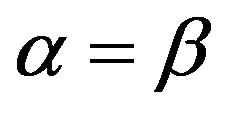 . Also, for some
. Also, for some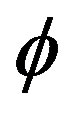 ,
,
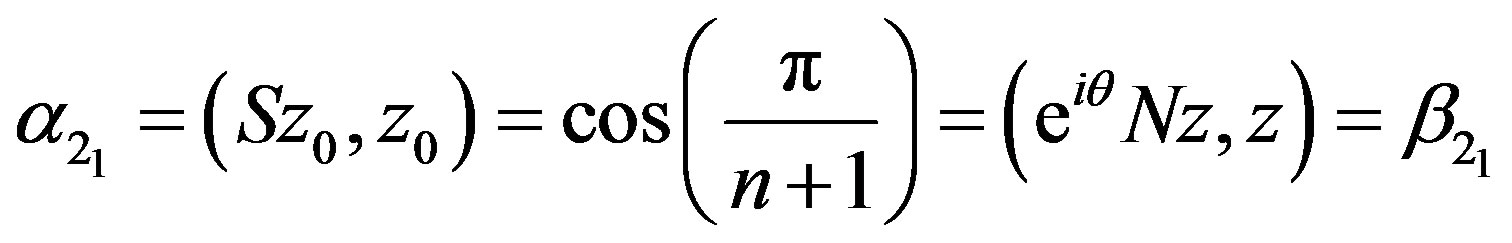 . Now by [1] [P.375, Lemma 2], we obtain:
. Now by [1] [P.375, Lemma 2], we obtain:
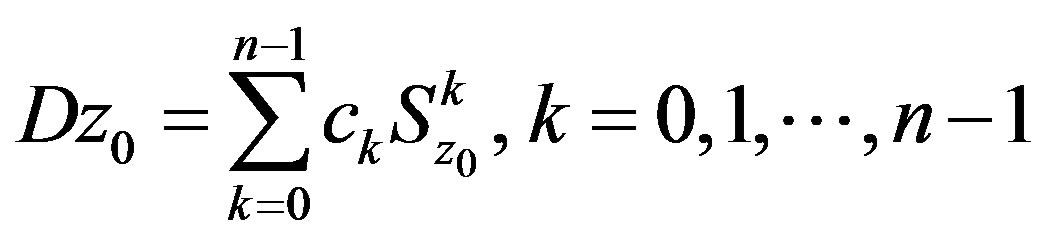
and

Let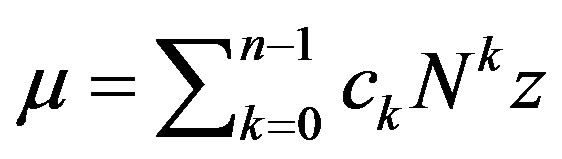 . Then:
. Then:
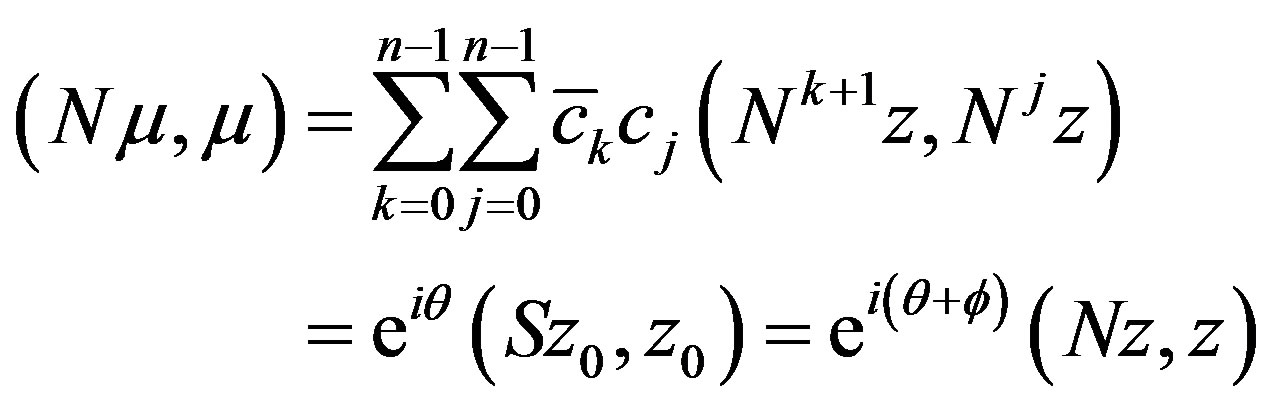
and the theorem follows from above since  is arbitrarily chosen.
is arbitrarily chosen.
3. An Application
An operator A is a unilateral weghted shift if there is an orthonormal basis 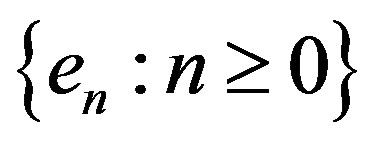 and a sequence of scalers
and a sequence of scalers 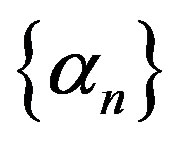 such that
such that 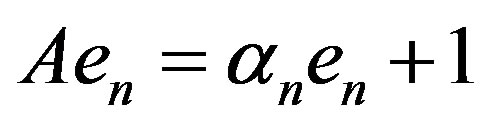 for all
for all . It is easy to see that
. It is easy to see that  where S is the unilateral shift and D is the diagonal operator with
where S is the unilateral shift and D is the diagonal operator with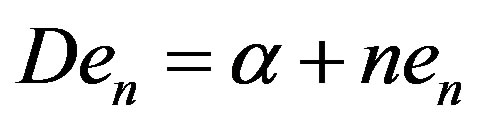 , for all n.
, for all n.
Thus, 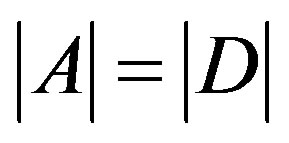 and
and  for all n. So
for all n. So 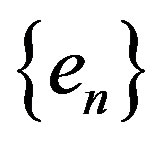 is the basis of eigenvectors for
is the basis of eigenvectors for . Also, note that A is bounded if
. Also, note that A is bounded if  is bounded.
is bounded.
If A is a unilateral shift then 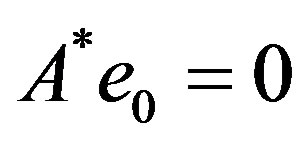 and
and  for
for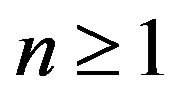 . Consequently, for a hyponormal operator A,
. Consequently, for a hyponormal operator A,  and
and 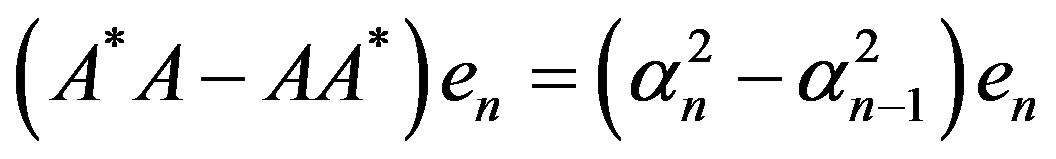 for
for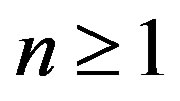 . A wighted shift is hyponormal if and only if its weight sequence is increasing.
. A wighted shift is hyponormal if and only if its weight sequence is increasing.
Example 3.1. Let 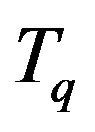 be an operator on
be an operator on 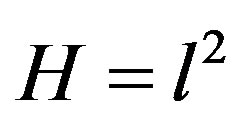 such that
such that 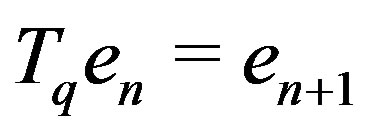 and
and  for
for 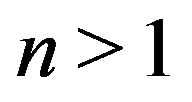 and
and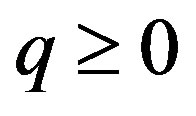 . Here, we show that
. Here, we show that  is not an eigenvalue of
is not an eigenvalue of 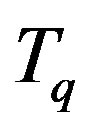 if
if
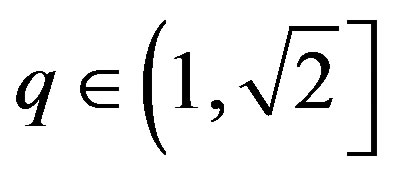 . We prove our claim by contradiction Let
. We prove our claim by contradiction Let 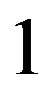 be an eigenvalue of
be an eigenvalue of . Then, there exists
. Then, there exists 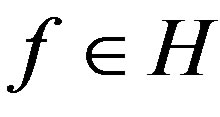 with
with 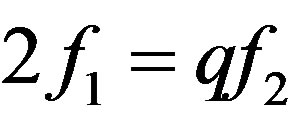 and
and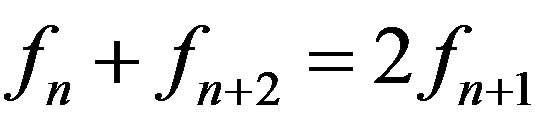 , n = 2, 3, ···. It is not hard to see that:
, n = 2, 3, ···. It is not hard to see that:
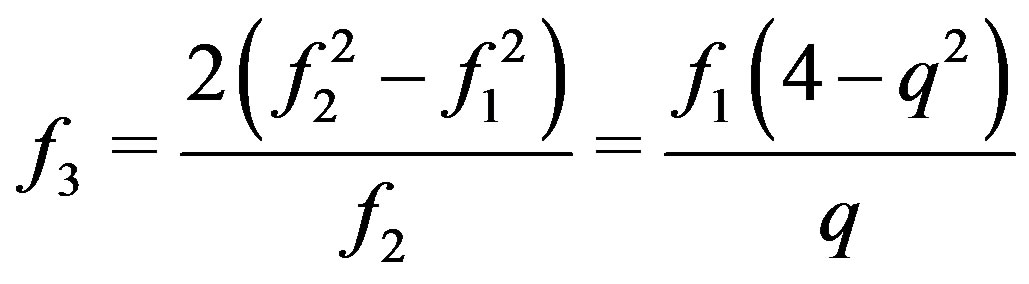
For , we have
, we have  and thus
and thus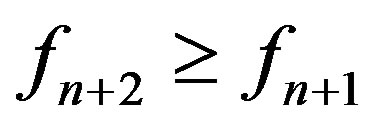 , which shows that
, which shows that , contrary to our assumption. Thus,
, contrary to our assumption. Thus, 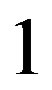 is not an eigenvalue of
is not an eigenvalue of 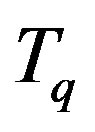 if
if
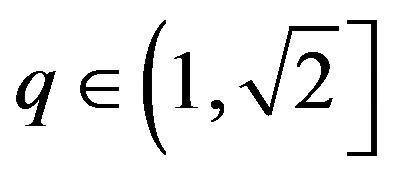 .
.
Remark 3.2. Following [2], if 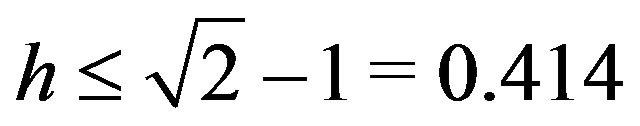 then
then
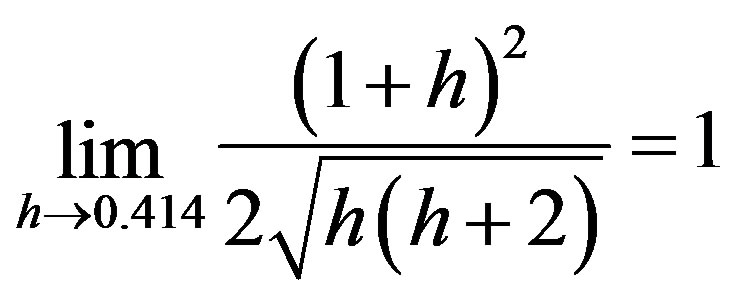
Therefore, the numerical radius, 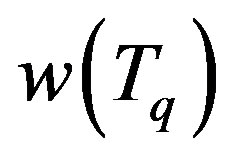 is equal to 1.
is equal to 1.
The example below shows that there exists an operator  such that
such that 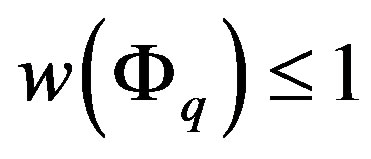 for
for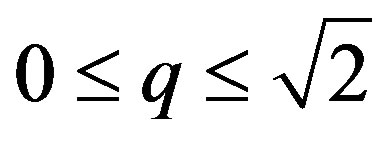 .
.
Example 3.3. Let  be a unilateral shift. If
be a unilateral shift. If  is the orthogonal projection of
is the orthogonal projection of  onto the spanning set of vectors
onto the spanning set of vectors  then
then  and
and  has the usual matrix representation. Let
has the usual matrix representation. Let
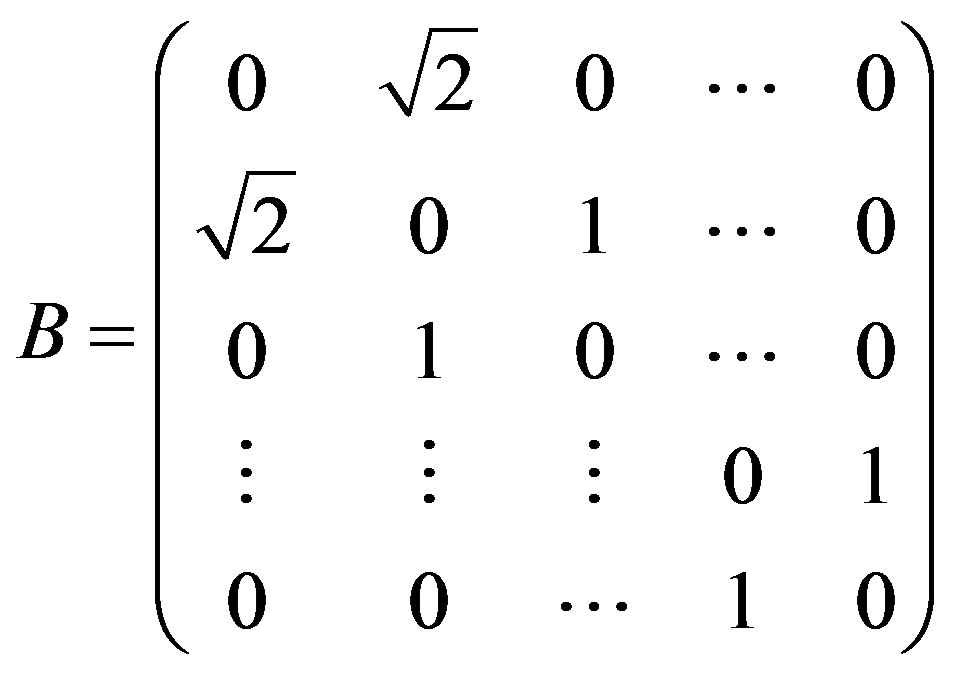
Then the characteristic polynomial of 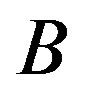 is given by a Chebyshev polynomial
is given by a Chebyshev polynomial 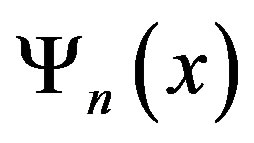 of the first kind. Let
of the first kind. Let 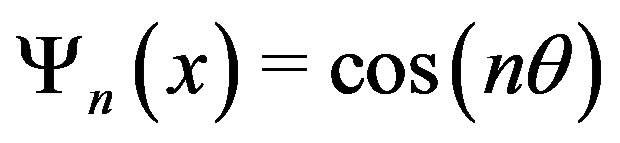 where
where . Then:
. Then:
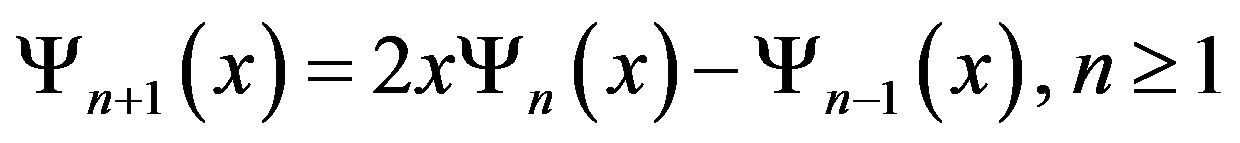
(easily proven by trigonometric identities) and 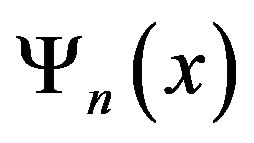 for
for  is a linear combination of powers of xk. Also, det
is a linear combination of powers of xk. Also, det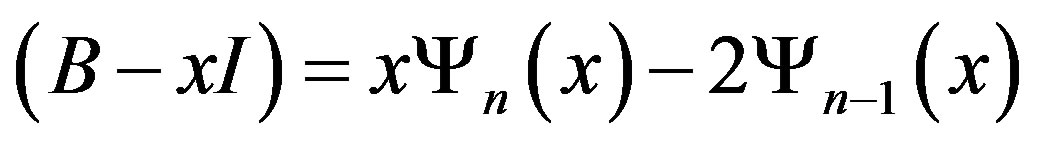 . If
. If 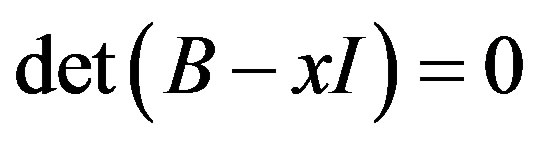 then the roots are given by the Chebyshev polynomial of the first kind. The roots can be found by finding the eigenvalues of matrix B. By [2, p. 179, Example 9], the eigenvalues of B are given by
then the roots are given by the Chebyshev polynomial of the first kind. The roots can be found by finding the eigenvalues of matrix B. By [2, p. 179, Example 9], the eigenvalues of B are given by
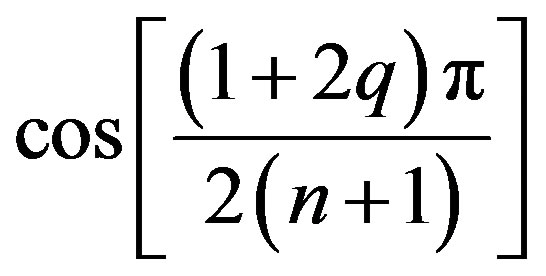 , for
, for .
.
Suppose that
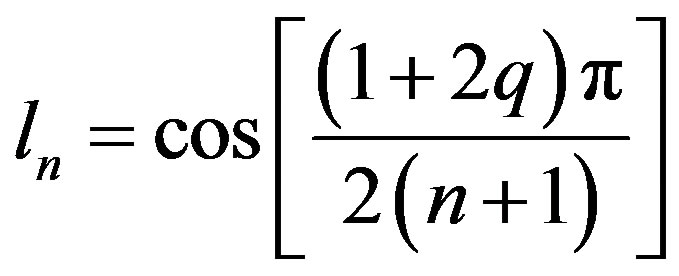
then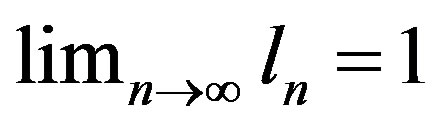 . Hence,
. Hence, 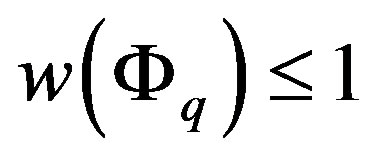 if
if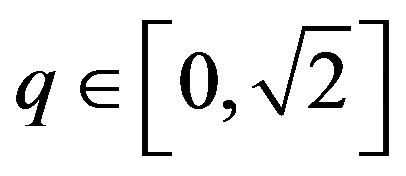 .
.
REFERENCES
- U. Haagerup and P. de la Harpe, “The Numerical Radius of a Nilpotent Operator on a Hilbert Space,” Proceedings of the American Mathematical Society, Vol. 115, 1999, pp. 371-379.
- C. A. Berger and J. G. Stampi, “Mapping Theorems for the Numerical Range,” American Journal of Mathematics, Vol. 89, 1967, pp. 1047-1055.
- M. T. Karev, “The Numerical Range of a Nilpotent Operator on a Hilbert Space,” Proceedings of the American Mathematical Society, Vol. 132, 2004, pp. 2321-2326.
- J. P. Williams and T. Crimmins, “On the Numerical Radius of a Linear Operator,” American Mathematical Monthly, Vol. 74, No. 7, 1967, pp. 832-833. doi:10.2307/2315808
- J. T. Scheick, “Linear Algebra with Applications,” International Series in Pure and Applied Mathematics, McGraw-Hill, New York, 1997.
- B. Sz.-Nagy and C. Folias, “Harmonic Analysis of Operators on a Hilbert Sapce,” North Holland, Amsterdam, 1970.

