Advances in Pure Mathematics
Vol.2 No.5(2012), Article ID:22796,4 pages DOI:10.4236/apm.2012.25042
On Discrete Adomian Decomposition Method with Chebyshev Abscissa for Nonlinear Integral Equations of Hammerstein Type
Department of Mathematics, Sciences Faculty for Girls, King Abdulaziz University, Jeddah, KSA
Email: h.o.bak@hotmail.com, darwishma@yahoo.com
Received April 10, 2012; revised May 11, 2012; accepted May 19, 2012
Keywords: Discrete Adomian decomposition method; Hammerstein; Chebyshev
ABSTRACT
We study approximate solutions of a nonlinear integral equation of Hammerstein type. We describe the principle of discrete Adomian decomposition method (DADM). DADM is considered in the case we evaluate numerical integration by using Chebyshev roots. This technique gives an accurate solutions as will shown by illustrate examples.
1. Introduction
Nonlinear integral equations appears very often in many applications. For example, it occurs in solving several problems arising in economics, engineering, and physics. One of the most important frequently investigated nonlinear integral equations is the Hammerstein integral equation (cf. [1-5]).
In this paper we study the problem of approximate solutions for the nonlinear integral equations of Hammerstein type, namely
 (1)
(1)
Adomian decomposition method (ADM) for solving integral equations has been presented by G. Adomian [6,7]. In [8,9], Wazwaz extended ADM to solve Volterra integral equations and boundary value problems for higher-order integro-differential equations. Numerous works have been focusing on the development of more advanced and efficient methods for nonlinear integral equations such as implicitly collocations methods [10], product integration method [11] and Adomian decomposition method [9,12]. There are significant interest in applying Adomian decomposition method (ADM) for a wide class of nonlinear equations. For example, ordinary and partial differential equations, integral equations and integro-differential equations, see [13-16] and references therein.
In [17], Behiry et al. introduced a discrete version of the Adomian decomposition method and applied it to Equation (1). This method is called a discrete Adomian decomposition method (DADM). DADM arises when the quadrature rules are used to approximate the definite integrals which can not be computed analytically. The DADM gives the numerical solution at nodes used in the quadrature rules.
It is worthwhile mention that Behiry and other [17] applied Simpson rule with  subinterval and step size
subinterval and step size
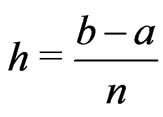 . It is occasionally useful, both theoretically and practically, to have interpolatory formulas on sets of abscissas other than the equidistant set. A common choice is the set of zeros of an orthogonal polynomial. By using the fact that the Chebyshev polynomials are one of the best orthogonal polynomials that have important role particularly in numerical analysis, we choose the nodes of the quadrature rule to be the zeros of Chebyshev polynomials in order to minimize the discretization error.
. It is occasionally useful, both theoretically and practically, to have interpolatory formulas on sets of abscissas other than the equidistant set. A common choice is the set of zeros of an orthogonal polynomial. By using the fact that the Chebyshev polynomials are one of the best orthogonal polynomials that have important role particularly in numerical analysis, we choose the nodes of the quadrature rule to be the zeros of Chebyshev polynomials in order to minimize the discretization error.
2. Chebyshev Polynomials
It is worth mentioning that, Chebyshev polynomials are everywhere dense in numerical analysis [18].
Definition 2.1. The Chebyshev polynomial  of the first kind is a polynomial in
of the first kind is a polynomial in  of degree
of degree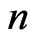 , defined by the following relation
, defined by the following relation
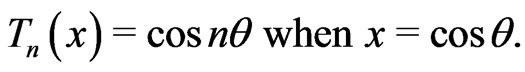 (2)
(2)
From Formula (2), the zeros for 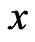 in
in 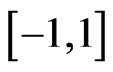 of
of 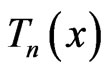 must correspond to the zeros for
must correspond to the zeros for  in
in 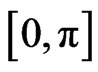 of
of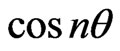 , so that
, so that

Hence, the zeros of 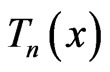 are
are
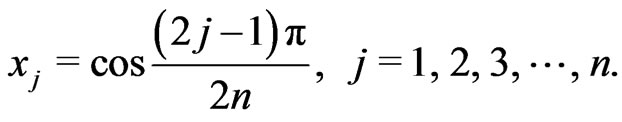 (3)
(3)
The internal extrema of 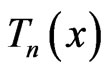 correspond to the extreme values of
correspond to the extreme values of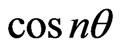 , namely the zeros of
, namely the zeros of , since
, since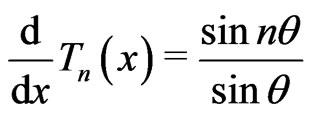 . Hence, including those at
. Hence, including those at
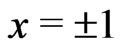 , the extrema of
, the extrema of  on
on  are
are
 (4)
(4)
3. DADM with New Nodes
The Adomian decomposition method (ADM) is now known as an efficient and accurate tool for deriving analytical solutions without linearization or perturbation for large classes of linear and nonlinear operator equations in different fields of applied mathematics, engineering and physics.
By applying ADM, the solution 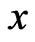 of Equation (1) is given by the following series form
of Equation (1) is given by the following series form
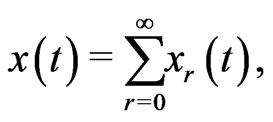 (5)
(5)
where the components ,
, 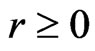 , can be computed later on. We represent the nonlinear term
, can be computed later on. We represent the nonlinear term  by the Adomian polynomials,
by the Adomian polynomials, 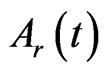 , as follows:
, as follows:
 (6)
(6)
where 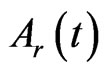 can be evaluated by the following formula, [7],
can be evaluated by the following formula, [7],
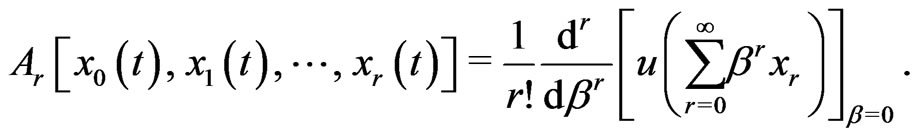 (7)
(7)
By substituting from (5) and (6) into (1), we obtain
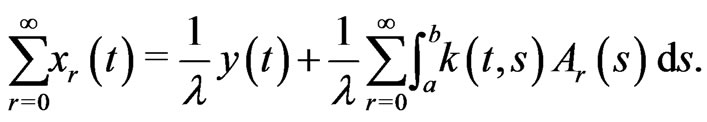 (8)
(8)
Now, we can compute the components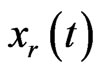 ,
, 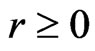 , by using the following recursive relations [19]
, by using the following recursive relations [19]
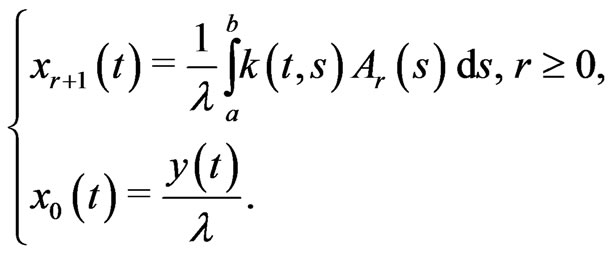 (9)
(9)
It is noticed that the computation of each component ,
,  , requires the computation of an integral in Equation (9). If the evaluation of integral in (9) is analytically impossible, the ADM can not be applied. So the quadrature rules are used to approximate the definite integrals. Now, we consider a numerical integration scheme given by the formula
, requires the computation of an integral in Equation (9). If the evaluation of integral in (9) is analytically impossible, the ADM can not be applied. So the quadrature rules are used to approximate the definite integrals. Now, we consider a numerical integration scheme given by the formula
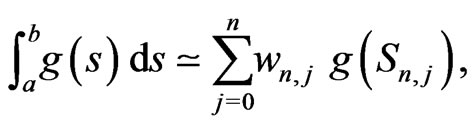 (10)
(10)
where  is a continuous function on
is a continuous function on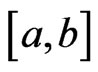 ,
,
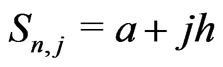 are the nodes of the quadrature rule,
are the nodes of the quadrature rule,
 and
and ,
,  , are the weight functions. From (9) and (10), we obtain
, are the weight functions. From (9) and (10), we obtain
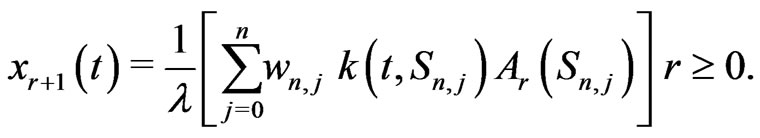 (11)
(11)
By collocating transformed Equation (11) at  points
points ,
, 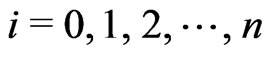 , which are the same points of quadrature rule, we get
, which are the same points of quadrature rule, we get
 (12)
(12)
The approximate solution of Equation (1) by using DADM can be obtained by summing the approximate values to the components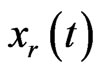 ,
,  , represented by Equation (12) at nodes
, represented by Equation (12) at nodes ,
,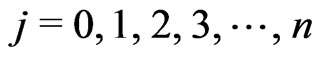 . In [17], Behiry et al. applied Simpson rule with number of subinterval
. In [17], Behiry et al. applied Simpson rule with number of subinterval 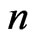 and step size
and step size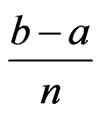 , Simpson’s rule is given by the formula
, Simpson’s rule is given by the formula
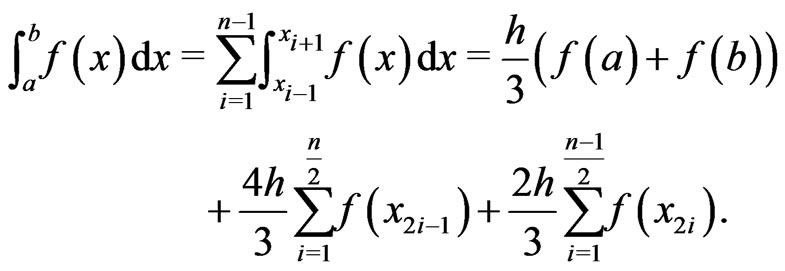 (13)
(13)
Approximating the definite integral in Equation (9) by applying formula (13) to get
 (14)
(14)
Then, discrete the independent variable at the nodes used for the quadrature rule in Equation (14).
Quadrature rules that are based on an expansion of the integrand in terms of Chebyshev polynomials employ a change of variables and use a discrete cosine transform approximation for the cosine series which have fast converging accuracy comparable to another quadrature rules. A cosine series converges very rapidly for functions that are even, periodic, and sufficiently smooth. This is true when we used Chebyshev polynomial to approximate the integrand function, since  is even and periodic in
is even and periodic in  and is
and is 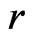 -times differentiable. In order to use numerical integration method with orthogonal polynomial as Chebyshev, we transform the interval
-times differentiable. In order to use numerical integration method with orthogonal polynomial as Chebyshev, we transform the interval  into the interval
into the interval 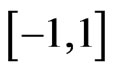 by using the transformation
by using the transformation
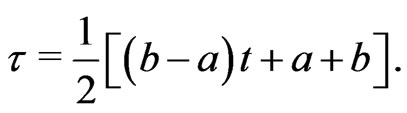
Applying this formula to Equation (9), we get
 (15)
(15)
Then we approximate the definite integral in Equation (15) by any quadrature rule using the zeros of Chebyshev polynomials form Equation (9) we can improve the accuracy of DADM as we show in the following examples.
4. Illustrative Examples
In this section we apply our methods to some integral equations of Hammerstein type. These examples show the efficient and accuracy of our method.
Example 4.1. Consider the nonlinear integral equation
 (16)
(16)
Here, 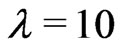 ,
, 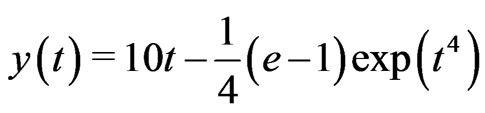 ,
,
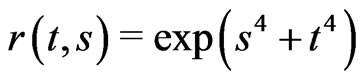 and
and . Equation (16) has an exact solution
. Equation (16) has an exact solution , [20].
, [20].
Let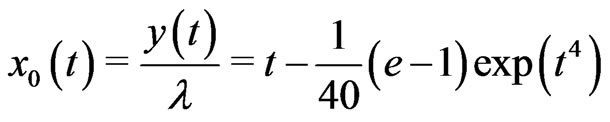 .
.
By using DADM with Simpson’s rule, the effect of 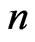 in absolute error at
in absolute error at 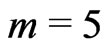 is shown in Table 1 while the effect of
is shown in Table 1 while the effect of 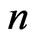 in absolute error at
in absolute error at 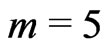 by using DADM with Chebyshev nodes is shown in Table 2.
by using DADM with Chebyshev nodes is shown in Table 2.
Example 4.2. Consider the nonlinear integral equation
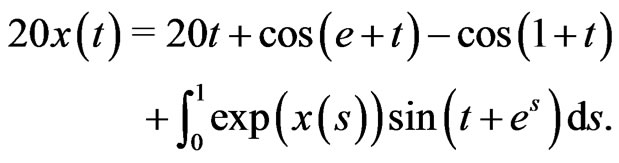 (17)
(17)
Here,  ,
, 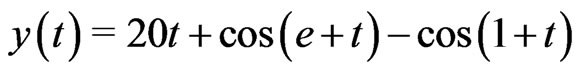 ,
,
 and
and . Equation (17) has an exact solution
. Equation (17) has an exact solution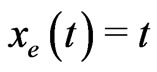 , [20].
, [20].
Let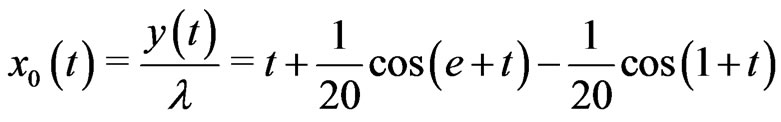 .
.
By using DADM with Simpson’s rule, the effect of  in absolute error at
in absolute error at  is shown in Table 3 while the effect of
is shown in Table 3 while the effect of  in absolute error at
in absolute error at  by using DADM with Chebyshev nodes is shown in Table 4.
by using DADM with Chebyshev nodes is shown in Table 4.

Table 1. The effect of n in absolute error at m = 5 by using DADM with Simpson’s rule.
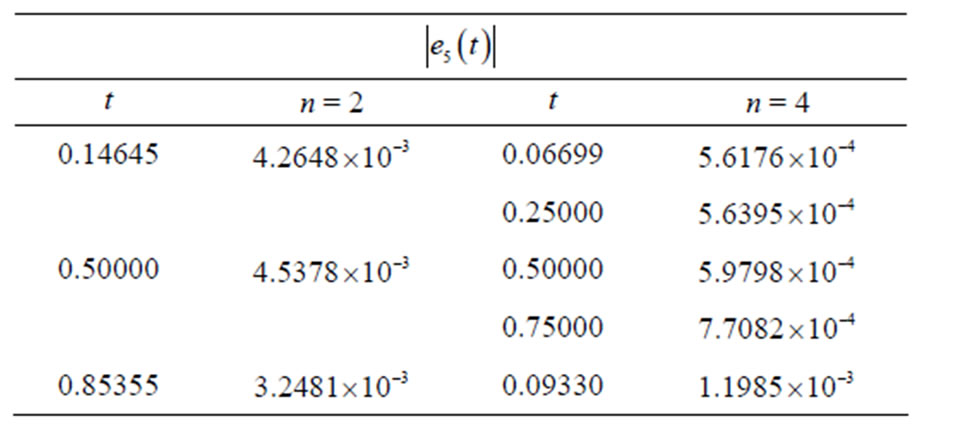
Table 2. The effect of n in absolute error at m = 5 by using DADM with Chebyshev nodes.

Table 3. The effect of n in absolute error at m = 5 by using DADM with Simpson’s rule.
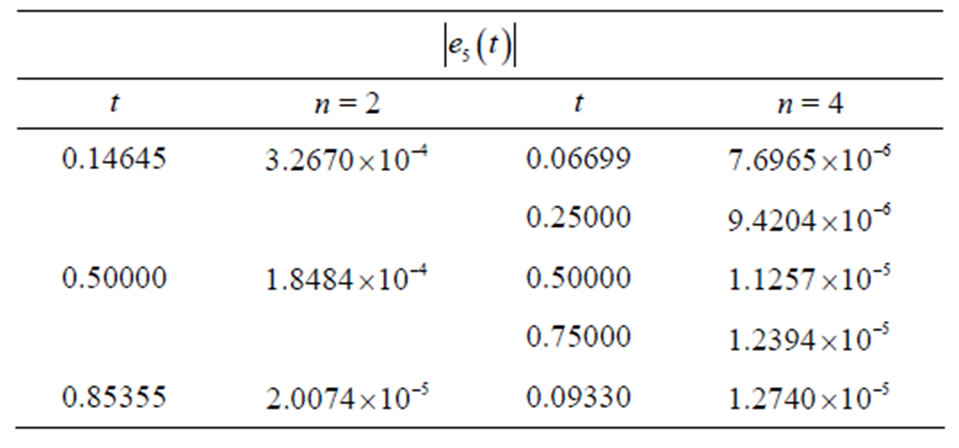
Table 4. The effect of n in absolute error at m = 5 by using DADM with Chebyshev nodes.
5. Conclusion
We have solved the nonlinear integral equation of Hammerstein type by using DADM and the zeros of Chebyshev polynomial. The properties of Chebyshev roots are used to rise the accuracy of the DADM. Our examples demonstrate the validity of the proposed method. The method can be extended and applied to the system of nonlinear integral equations and nonlinear integral equations of Volterra type, but some modifications are required.
REFERENCES
- J. Appell and C. Chen, “How to Solve Hammerstein Equations,” Journal of Integral Equations and Applications, Vol. 18, No. 3, 2006, pp. 287-296. doi:10.1216/jiea/1181075392
- K. Deimling, “Nonlinear Functional Analysis,” SpringerVerlag, Berlin, 1985. doi:10.1007/978-3-662-00547-7
- A.A. El-Bary, “Sobolev’s Method for Hammerstein Integral Equations,” Computers & Mathematics with Applications, Vol. 11, No. 2, 2006, pp. 91-94.
- X. Liu, “On a Nonlinear Hammerstein Integral Equation with a Parameter,” Nonlinear Analysis, Vol. 70, No. 11, 2009, pp. 3887-3893. doi:10.1016/j.na.2008.07.038
- D. O’Regan and M. Meehan, “Existence Theory for Nonlinear Integral and Integrodifferential Equations,” Kluwer Academic Publishers, Dordrecht, 1998. doi:10.1007/978-94-011-4992-1
- G. Adomian, “A Review of the Decomposition Method in Applied Mathematics,” Journal of Mathematical Analysis and Applications, Vol. 135, No. 2, 1988, pp. 501-544. doi:10.1016/0022-247X(88)90170-9
- G. Adomian, “Solving Frontier Problems of Physics: The Decomposition Method,” Kluwer Academic Publishers, Dordrecht, 1994.
- A. M. Wazwaz, “A Reliable Treatment for Mixed Volterra-Fredholm Integral Equations,” Applied Mathematics and Computation, Vol. 127, No. 2-3, 2002, pp. 405-414. doi:10.1016/S0096-3003(01)00020-0
- A. M. Wazwaz and S. M. El-Sayed, “A New Modification of the Adomian Decomposition Method for Linear and Nonlinear Operators,” Applied Mathematics and Computation, Vol. 122, No. 3, 2001, pp. 393-405. doi:10.1016/S0096-3003(00)00060-6
- H. Brunner, “Implicitly Linear Collocation Methods for Nonlinear Volterra Equations,” Applied Mathematics and Computation, Vol. 9, No. 3-5, 1992, pp. 235-247.
- T. Tang, S. McKee and T. Diogo, “Product Integration Methods for an Integral Equation with Logarithmic Singular Kernel,” Applied Numerical Mathematics, Vol. 9, No. 3-5, 1992, pp. 259-266. doi:10.1016/0168-9274(92)90020-E
- N. Bildik and M. Inc, “Modified Decomposition Method for Nonlinear Volterra-Fredholm Integral Equations,” Chaos Solitons Fractals, Vol. 33, No. 1, 2007, pp. 308- 313. doi:10.1016/j.chaos.2005.12.058
- H. L. Arora and F. I. Abdelwahid, “Solution of NonInteger Order Differential Equations via the Adomian Decomposition Method,” Applied Mathematics Letters, Vol. 6, No. 1, 1993, pp. 21-23. doi:10.1016/0893-9659(93)90140-I
- M. M. Hosseini and H. Nasabzadeh, “Modified Adomian Decomposition Method for Specific Second Order Ordinary Differential Equations,” Applied Mathematics and Computation, Vol. 186, No. 1, 2007, pp. 117-123. doi:10.1016/j.amc.2006.07.094
- D. Kaya, “The Use of Adomian Decomposition Method for Solving a Specific Nonlinear Partial Differential Equations,” Bulletin of the Belgian Mathematical Society Simon Stevin, Vol. 9, No. 3, 2002, pp. 343-349.
- S. Shah, A. Shaikh and S. H. Sandilo, “Modified Decomposition Method for Nonlinear Volterra-Fredholm Integrodifferential Equation,” Journal of Basic & Applied Sciences, Vol. 6, No. 1, 2010, pp. 13-16.
- S. H. Behiry, R. A. Abd-Elmonem and A. M. Gomaa, “Discrete Adomian Decomposition Solution of Nonlinear Fredholm Integral Equation,” Ain Shams Engineering Journal, Vol. 1, No. 1, 2010, pp. 97-101. doi:10.1016/j.asej.2010.09.009
- J. C. Mason and D. C. Handscomb, “Chebyshev Polynomials,” CRC Press, New York, 2003.
- A. M. Wazwaz, “A First Course in Integral Equations,” World Scientific Publishing, Singapore City, 1997.
- A. Jerri, “Introduction to Integral Equations with Applications,” John Wiley & Sons, New York, 1999.

