ABSTRACT

A chemical non-equilibrium equation for binding of massless quarks to antiquarks, combined with the spatial correlations occurring in the condensation process, yields a density dependent form of the double-well potential in the electroweak theory. The Higgs boson acquires mass, valence quarks emerge and antiparticles become suppressed when the system relaxes and symmetry breaks down. The hitherto unknown dimensionless coupling parameter to the superconductor-like potential becomes a re- gulator of the quark-antiquark asymmetry. Only a small amount of quarks become “visible”―the valence quarks, which are 13% of the total sum of all quarks and antiquarks―suggesting that the quarks-antiquark pair components of the becoming quark- antiquark sea play the role of dark matter. When quark-masses are in-weighted, this number approaches the observed ratio between ordinary matter and the sum of ordinary and dark matter. The model also provides a chemical non-equilibrium explanation for the information loss in black holes, such as of baryon number.

Keywords:

Confinement of Quarks, Higgs Mechanism, Emergence of Mass, Dark Matter, Valence Quarks, Antiquark Suppression, Black Holes, Dark Energy

1. Introduction

Two ways for explaining the origin of mass, QCD and confinement of quarks and the Higgs-mechanism in the electroweak (EW) theory have been discussed by Wilczek: “Superficially those mechanisms appear quite different, but at a fundamental level they are essentially the same” [1] . Such a relationship is derived here in a chemical non- equilibrium model for binding massless quarks to their respective antiquarks. The model yields the same type of superconductor-like potential that generates mass in the EW theory, however the earlier unknown dimensionless coupling to the potential becomes a regulator of the quark-antiquark asymmetry. Only a fraction of the quarks, 13% of the total sum of all once free quarks and antiquarks, become “visible” as valence quarks, suggesting that excited pairs of the “invisible” non-valence quarks and the “invisible” antiquarks could play the role of dark matter in a remote quasi-free state. The model also provides an explanation as to how valence quarks emerge by suppression of antiquarks.

The Sakharov constraints [2] ―violation of C and CP symmetry and baryon number conservation, in a thermodynamic non-equilibrium Universe which still expands from a super-dense state―are partly relevant also for these studies. However, to create a pro- ton or neutron, with massive valence quarks and a spatially correlated quark-antiquark sea from a gas-like state of equal densities of free massless quarks (q) and antiquarks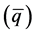, the gas must also condense and the number (density) of quarks must increase relative to the number (density) of antiquarks. This implies that the binding of quarks to antiquarks takes place at chemical non-equilibrium conditions. In combination with strong spatial correlations that emerge in the condensation process, such conditions― an increasing density of quark-antiquark 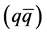-pairs (ψ) and a density of quarks (becoming valence quarks) that increases relative to that of antiquarks―are very unfortunate, because the grand canonical ensemble then admits only fluctuations (fugacity) about a constant number of particles [3] . The problem therefore also goes beyond lattice QCD, which relies on the grand canonical ensemble and more “thermotropic” type conditions [4] .

Quark-gluon interaction is strong at distances of about a nucleon diameter (10⁻¹⁵ m), but weakens at high energies (temperatures) where quarks interact at shorter distances. Already at about 150 MeV (~2 × 10¹² degrees K), nuclear matter boils down to a quark- gluon plasma (QGP) [4] , which behaves like a fluid with small shear viscosity (short mean free path) and a very high opaqueness towards color, not unlike electromagnetic Debye screening in a usual plasma. At infinite energy, quarks become asymptotically free [5] [6] and attain the same density as antiquarks. Conversely, when nuclear matter cools down and condenses, the couplings and spatial correlations between quarks and antiquarks become strong and a surplus of valence quarks emerge. Neither transport theory can solve this chemical non-equilibrium problem [4] . Apart from that, QCD also has a complicated singular infrared behavior [7] [8] that flaws calculations of bound states.

This paper identifies and suggests solutions to some of these problems that underlie the standard model. Section 2 describes the chemical non-equilibrium equation for binding of quarks (fermions) to antiquarks (antifermions). The binding equation, combined with a coherent (local) formulation of the strong spatial (non-local) correlations between the condensing particles, as shown in Section 3, yields the Ginsburg-Landau (GL) like potential used in EW theory, however, with a density-dependent order parameter. Section 4 provides an explanation as to how mass, dark matter, and valence quarks emerge by suppression of antiquarks. It is shown that the coupling to the GL- like potential becomes a regulator of the -asymmetry, leaving only valence quarks, which are about 13% of the total sum of all quarks and antiquarks, “observable”. When the different effective quark-masses are in-weighted, this value approaches the observed ratio between ordinary and dark matter. Section 5 discusses possible implications of this density-dependent model for general relativity (GR), black holes, gravitational waves, and expansion and inflation of the Universe.

2. Nonequilibrium Quark-Antiquark Binding

The chemical non-equilibrium conditions exclude usual quantum field theory methods, such as the Bethe-Salpeter equation and eikonal type models [9] [10] , to describe the binding of quarks or leptons to their respective antiparticles. Instead, the model is founded on three dynamical constraints: 1) an equation for chemical non-equilibrium binding of massless quarks to massless antiquarks, 2) the initial boundary constraints for the quark and antiquark scalar field amplitudes q and, which are assumed equal for left- and right-handed fermions, and 3) the strong spatial correlations between the -pairs. These field amplitudes, which measure the non-equilibrium deviations from the usual chemical equilibrium type quantum fields, are linearly proportional to the respective particle numbers and can hence be treated as “densities”as long as the particles are massless and unobservable.

The rate-equation for chemical non-equilibrium binding of massless quarks to antiquarks when the system cools down, is given by

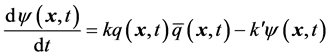, (1)

k and being the binding and unbinding constants. Spinors are not needed, because quarks (fermions) can bind to antiquarks (antifermions) only when the particles are approximately at rest relative to each other and then exchange only soft quanta. Equation (1) thus corresponds to a form of coherent approximation. Recall that the aim is not to describe relativistic scattering of differently handed chiral fermions, but just the increase in the numbers (densities) of bound 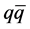-states and valence quarks. This does not exclude that k and k’ may depend on scattering effects. Observe also that Equation (1) goes in both directions―to the right when the system cools down and to the left when the temperature (energy) increases―and should hence be suitable to describe hadronization-fragmentation processes.

Equation (1) also obeys the initial boundary constraints

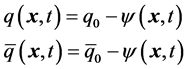, (2)

and that the initial “free” quark and antiquark amplitudes, q₀ and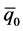, should be equal in magnitude at the big bang, in extremely high-energy proton-proton collisions, and supposedly also in the central region of black holes.

After insertion of these constraints, Equation (1) reads

(3a)

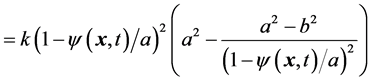, (3b)

where, , and.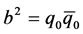

The solution to Equation (3) is

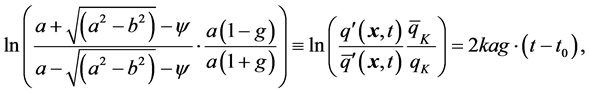(4)

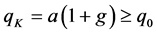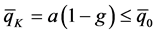where the “short-hand” notations and are the screening and screened initial quark and antiquark field amplitudes, and is a dimensionless parameter. Accordingly, and are the corresponding time- dependent field amplitudes in analogy with Equation (2). It is assumed that the binding process starts with a small fluctuation in favour of quarks, which is then maintained by Equation (3). Free massless quarks then compete to bind free massless antiquarks, but it may well be the opposite. The physical meaning of q_K and becomes more directly clear when K approaches zero. The screening effect then decreases with, and at the fields q_K, , and become the usual “bare” fields q₀, , q and, g vanishes and Equation (1) then yields the rate of stable binding only.

To quantify the screening effect and study the emergence of valence quarks, mass and dark matter by suppression of antimatter when the system cools down, however, Equation (3) must be first combined with the spatial correlations between the - pairs that encompass their condensation into hadrons. Like in a freely jointed chain (FJC) [11] , but regardless of whether the particles are tethered or not, the conformational distribution of the increasing indefinite number of -pairs over an infinite set of sites in the volume of a becoming baryon or a Higgs boson is

. (5)

However, to make the emerging particles point-like, Equation (5) must be contracted and synchronized to a fictitious “centre of mass”,. By this approximation, implying that ψ(x, t) is also instantly equalized within the small particle volume after each binding, Equation (5) becomes a geometric series that can be combined with Equation (3) provided that. Similar conditions should prevail in high-energy proton collisions. Should the Higgs boson turn out to have an internal structure, one possibility would be to describe this by the radius of gyration, which would yield a form factor [12] [13] .

After a certain time, , before the -pairs have started to become stably bound, unstable bindings are assumed to attain a stationary state,. Equation (5) then acquires a constant zero order term y_s, which can be factorized out also from higher order terms. If ψ_s is identified with, the joint probability density φ(x, t) of having a constant density of unstably bound -pairs, and an increasing indefinite density (number) of stably bound -pairs in the hadron at time t, becomes

, (6)

which can be combined with Equation (3). Equation (6), which has the form of a Bose- Einstein distribution, also corresponds formally to the grand partition function, with playing the role of “fugacity” [3] . However, is here driven off chemical equilibrium by Equation (3), which regulates the time-evolution of the system of valence quarks and stable and unstable -pairs in a density dependent manner.

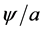
To obtain the relaxation dynamics and time evolution of the correlated system, Equation (6) must be linked to Equation (3). The time derivative of Equation (6),

, (7)

combined with Equation (3) then yields

, (8)

which has the solutions

. (9)

To create a baryon with a small finite number (one or two) of valence quarks (Figure 1(c)) of a certain flavour, and a sea of -pairs in which all antiquarks are bound by quarks, or a boson (Figure 1(b)), massless antiquarks must be exposed to massless quarks for a certain time. It is also required for the system to relax and the symmetry to break down. The field j(t) can then be normalized by a topological quantization [14] , , where N_p is the number of stably

bound -pairs with mass m_p, and. But N_p is also proportional to the number of valence quarks of a certain flavour, Q_f, because equals the difference between the “densities” of quarks and antiquarks. In principle, any finite number of valence quarks of a certain flavour could be factorized out like in Figure 1(c), by first dividing the alternating sequence in Figure 1(b) into Q_f identical infinite sequences, each of which is then rearranged as in Figure 1(c).

By the topological quantization, the stationary zero order term of unstable -pairs in Equation (6), , is automatically subtracted out. The flaw with negative density, , is as usual remedied by a field displacement, , which causes the symmetry breakdown (Figure 2). However, contrary to the ad hoc displacement in EW theory, the symmetry break is here due to the relaxation of a defined density-dependent collective dynamics, by which the system’s mass increases from zero to (Figure 2(b)). Also noteworthy is that the infinite number of massless -pairs in Figure 1(c) has decreased after the topological quantization, to a definite finite number N_p of massive pairs.

3. Derivation of a GL-Like Potential

By the contraction of all (x, t) to a fictitious “centre of mass” (x, t)―an approximation needed to derive the dynamics and to make all particles point-like―the internal structure and dynamics of the system were neglected. However, in principle, Equation (5)

could correspond to any arbitrary structure and dynamics.

For simplicity the time dependent solution in Equation (9) is interpreted as a travelling wave on a string-like 1D lattice of -pairs (Figure 1(b) and Figure 1(c)), with a travelling wave velocity equal to the binding rate constant k. Equation (8) can then be written as

, (10)

hence

. (11)

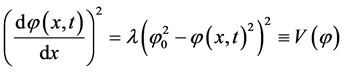
This V(φ), which corresponds to a continuum approximation dynamics [15] of the discrete “lattice” in Equation (5), now equals the GL-like potential of the scalar field component that remains non-zero in the unitary gauge of the EW model, and λ = g² as the hitherto unknown dimensionless parameter [16] . However, in this collective model, V(φ) is the density-dependent, hence lyotropic [17] , potential energy of the chemical non-equilibrium system of quarks and antiquarks (Figure 2(c)), and leptons and antileptons, and λ = g² has become a regulator of the antiparticle suppression as will be further explained below.

The derivative of Equation (11) yields the spatial part of the equation of motion

, (12)

albeit for a particle with imaginary mass. This flaw too is restored by the displacement. The potential energy then changes into (Figure 2(d))

, (13)

and the corresponding equation of motion reads

. (14)

The mass term is now real and identified with the Higgs boson mass. The solution to Equation (14) has become positive definite and describes the gradual emergence of mass, i.e. the gradual approach to (Figure 2(b)).

. (15)

However, the corresponding field displacement caused by the relaxation and condensation of the actual many-body system, does not take place until after all quarks except for a small number of valence quarks (Figure 1(c)), have been pairwise stably bound to antiquarks.

4. Quark-Antiquark Asymmetry

This chemical non-equilibrium model yields a quark-antiquark asymmetry, and, by which antiquarks become suppressed relative to quarks according to with. All antiquarks, except those in the stationary state, thus vanish in the limit. A small dominance of quarks―becoming valence quarks―over antiquarks, with, suffices for all antiquarks to bind to quarks and become supressed in the -sea. This type of relaxation dynamics is assumed to take place after a big bang and after high-energy proton- proton collisions, and probably also in black holes. The value of g is derived from m_H = 2gφ₀, and with m_H = 125.09 GeV and φ₀ = 174.22 GeV [16] one has , hence.

This determines in turn the dimensionless parameter which now yields the -asym- metry, , the probability to observe the surplus of valence quarks, relative to the sum of all quarks and antiquarks. As explained below, this expression is approximately equal to the ratio between the amount of visible mass and the sum of visible and “invisible” (dark) masses, because the density of valence quarks is proportional to the density of nucleons in the Universe. The theoretically derived λ ≈ 0.13 agrees well with the 4.9/30.8 = 0.159 observed [18] , and has also the same correct order of magnitude as the ratio 380,000 years after big bang. It thus appears as if that the Higgs boson is just a quark-antiquark condensate, which is obviously not so because leptons, photons and gluons also contribute to the particle masses [1] . However, g still depends only on the quark or lepton field amplitudes regardless of flavour and mass.

The topological quantization, , in combination with the contraction of Equation (5) to Equation (6), provides a model-explana- tion as to how the infinite gas-like system of equal amounts of uncorrelated massless quarks and antiquarks, hence without a surplus of quarks, is condensed into a finite system of -pairs which also contains valence quarks. Equation (1) first generates the highly excited, infinite lattice in Equation (5) of massless -pairs (N_p ® ¥; m_p ® 0). The condensation implied by Equation (6) can then proceed in two different ways, leading to absence (Figure 1(b)) or presence (Figure 1(c)) of valence quarks. However, the existence of massive valence quarks in baryons indicates that the -pairing driven by Equation (1) has proceeded as in Figure 1(c). The topological quantization can then hopefully help to explain how the infinite system of massless -pairs, in this model represented by Equation (6), cools down and relaxes into a finite sea of massive -pairs described by Equation (15), a classical kink event [14] with amplitude.

Since quarks are initially free and massless, at infinite energies essentially only photons contribute to the infinite energies to the initial binding of quarks by antiquarks and to the induction of mass, and gluons contribute later at finite energies. The number of valence quarks Q_f ≤ 2, with flavour f and mass m_f, is related to the number N_p of -pairs and to the Higgs boson mass by. One may speculate that three valence quarks of two different flavours, such as in protons and neutrons, should require a two-dimensional lattice. The first bracket in bold types Figure 1(b) could similarly illustrate how a massive boson would become frozen out from the infinite lattice of pairs. A combination of such a system with the previous one could then yield massive baryons with three, five [19] [20] , seven or even more quarks.

These model derivations, which should hold for each separate flavour, also hold for charged leptons, which contribute similarly to the ratio between ordinary and dark matter. For instance, a condensate of massless electrons and positrons can produce para-positronium spin-zero atoms with a lifetime τ_p that decreases from infinity to 2ħ/(m_ec²α⁵)~1.25 × 10⁻¹⁰ s when the electron mass m_e increases from zero to 511 keV, α being the fine structure constant. Since τ_p is about 10¹² times longer than the lifetime of a Higgs boson, τ_H = 1.56 × 10⁻²² s, such a lepton condensate can thus also contribute to the GL-like potential and to the Higgs boson. Leptons probably contribute much less than baryons to the total mass of the Universe [1] , however, this is also a question of abundance, such as of neutrinos and maybe other weakly interacting massive particles (WIMPs).

The actual model can also explain the binding of massless neutrinos (n_K) to massless anti-neutrinos () if the binding force carrier underlying the contact interaction in Equation (1) is the soft initially massless Z⁰-boson. The coupling g then acquires the same form as given by Sakharov without proof in 1967, , and from which he estimated the C asymmetry to about 10⁻⁹ [2] . Accordingly, the ratio between the ordinary mass and the sum of ordinary and dark masses has the same form and value for all quarks and leptons, hence with g² = 0.13, explaining why all antiparticles are so rarely observed outside laboratories. As is well-known neutrino flavour oscillations yield information about the neutrino mass differences [21] [22] . But obviously, neutrinos do not slow down from the velocity of light and acquire mass instantly, because the pair-creation process with concomitant emergence of mass proceeds gradually (Figure 2(b)). However, since neutrinos are the lightest and most abundant massive particles, they might eventually contribute more information about dark matter and dark energy than other massive particles.

A softly bound condensate of up and down -pairs, becoming neutral pions, with a lifetime 84 × 10⁻¹⁸ s much longer than that of a Higgs boson, can hence also contribute to the scalar field and the Higgs boson. Since g equals the Higgs boson mass divided by, which is about two top-quark masses. One might hence speculate that the anti-top- quark is a major contributor to dark matter. However, clearly precursor condensates of all type of quarks, with lifetime decreasing from infinity down to the respective finite lifetime, when the mass increases from zero to the actual mass, can contribute too. The asymmetric contribution is apparently the sum of non-valence quarks, , and antiquarks, both of which are not directly visible.

To derive one tacitly had to assume that all valence quarks, non-valence quarks and antiquarks have the same effective mass, about 340 MeV. All particles in the denominator of l were hence weighted equally by a phenomenological factor θ = 1. This is the maximal mass acquired by valence quarks in the confined state in nucleons, which also contain the -sea. In the actual model, this mass is identified as the ordinary mass that has emerged gradually as a classical kink event [14] after a completed relaxation-conden- sation process and after symmetry breakdown of dynamics at the very end of the classical kink [14] in Equation (15).

The dark mass candidates available in this model are thus identified as the -pair components of the becoming -sea, before the end of the classical kink (Figure 2(b)). Therefore, these components should have a lower average effective mass, implying that in the denominator of λ should be weighted by a factor θ < 1, whereas valence quarks still have full effective mass (θ = 1) at the end of the curve in Equation (15). With and θ = 85%, the dimensionless coupling g equals which yields λ = g² = 0.159 in agreement with the value observed [18] .

If quarks and antiquarks in the stationary state can acquire mass before symmetry breakdown, their masses should have opposite signs and their gravitational contributions, one attractive and one repulsive, should cancel if quarks and antiquarks are not too far separated. However, at larger separations, such a repulsive form of gravitation could eventually drive the expansion of the universe. The same reasoning should hold for leptons.

5. Summary and Conclusions

A density-dependent, hence lyotropic [17] , form of the double-well potential employed in EW theory has been derived from a chemical non-equilibrium dynamics that describes the confinement of quarks. The model, which is a mean-field theory, shows that the Higgs mechanism and the confinement of quarks are essentially the same [1] . This relationship obtains by combining three different keys: Equation (1), the chemical non-equilibrium binding of quarks to antiquarks, Equation (2), the initial boundary constraints for these two reactants, and Equation (6), the strong spatial correlations between quark-antiquark pairs that emerge when the system cools down. One also had to redefine the initial quark field amplitudes, q₀ and, as and, hence, in accordance with the fluctuations that probably started big bang. The combination of these tools was in turn key to solve the underlying statistical mechanical problem, allowing for an increasing chemical potential in a system of strongly correlated particles. The model provides explanations to the emergence of mass, dark mass and valence quarks, by suppression of antiquarks.

It is still not possible to predict the mass of the Higgs boson. However, in this model, yields an estimate of the quark- antiquark asymmetry, the “observable” ratio between the densities of valence quarks and the sum of quarks and antiquarks, which can be related to the ratio between visible mass and all masses in the universe. The denominator, , which like the numerator has dimension mass, suggests that an amount equal twice that of antiquarks―the sum of non-valence quarks and antiquarks in hot condensates of such pairs, i.e. components of the becoming -sea―play the essential role of dark mass. Even without the phenomenological correction, θ = 0.85, the derived λ = 0.13 has the correct order of magnitude and thus yields a realistic estimate of the observed ratio, 0.159 [18] , between the amount of visible mass and the sum of visible and dark masses.

This chemical non-equilibrium type of dynamics is assumed to have controlled the relaxation dynamics after big bang when baryonic matter with a “surplus” of valence quarks was frozen out from a hot gaseous Universe with equal amounts of massless quarks and antiquarks. It is assumed to also control the relaxation after high-energy proton-proton collisions, and probably also essential parts of the dynamics in black holes.

Obviously, it would have been preferable to obtain the binding of quarks to antiquarks by exchange of gauge particles in 4D. However, the emergence of valence quarks―an increasing number of quarks relative to the number of antiquarks―implies chemical non-equilibrium conditions. In combination with strong spatial correlations, here represented by Equation (6), that emerge when quarks condense via a plasma phase [4] into point-like particles, the chemical non-equilibrium becomes a crucial statistical mechanical problem [3] beyond reach for the grand canonical ensemble which allows, at most, fluctuations about a constant number of particles, and hence beyond lattice QCD. Such non-equilibrium conditions also go beyond transport theories and string models, and a Bethe-Salpeter calculation of the binding mechanism in QCD would become too complicated even at equilibrium conditions. Unable to obtain the quark-antiquark binding by exchange of photons and gluons, the actual two-steps approach to the questions of emergence of mass, dark matter, and valence quarks, thus seems to be the best option at this stage; first the density-dependent GL-like potential is derived, by combing Equation (3) with Equation (6), and then this potential is inserted into the EW theory.

The Nielsen-Olesen (NO) string [23] can perhaps illustrate how the abelian part of the EW theory would behave with variable field amplitudes. The cosmic NO-type string would then as usual be defined by two coaxial core cylinders, one with a radius equal to the penetration depth λ = 1/m_Z of the gauge vector field A, and one with a radius equal to the coherence length ξ = 1/m_H, the inverse of the Higgs boson mass (Figure 3).

The inverse mass m_Z of the Z-boson plays the role of penetration length in this density-dependent superconductor-like model [24] . However, the penetration depth and the coherence length are here regulated by the lyotropic conditions, with and, implying firm restrictions for the string’s existence. Except for this density dependence and constraints, the derived collective GL-like potential seems to work almost in the same way as in the usual EW theory.

Spontaneous symmetry breaking occurs in many condensed matter systems such as superconductors, ferromagnets and crystals. In the actual chemical non-equilibrium den- sity-dependent [17] liquid crystal-like system, mass and valence quarks (baryons) emerge

as topological defects [14] (hence no ether) in an otherwise empty space, except for electro-magnetism and gravitation. Unstably bound particles and antiparticles, such as those in the stationary state, exist only in and about excited hot areas in space. The model works equally well driven backward by Equation (1), suggesting that it could also simulate the excitatory dynamics in black holes when the mass-energy density increases infinitely towards the central singular region, leading to creation of pairs of dust-like particles, which finally become massless in a dynamics with restored symmetry (Figure 2(c)). However, if antiparticles acquire a negative mass, as suggested before, this should imply a repulsive form of gravitation alongside with the normal attractive one. This could reduce the infinite increase of gravitation and singular behaviour of GR in the central region of black holes. At longer distances, such a negative gravitation could perhaps also drive the observed expansion of the Universe attributed to the cosmological constant (dark energy) in GR.

Given that 4.9% of all mass is visible (m_v), the actual model yields 25.9% dark mass (m_d), which leaves 69.2% dark energy (e_d). The model thus gives the correct order of magnitude for the ratio between visible and non-visible mass. However, since both the visible and the dark masses started from zero at the big bang, this model should comply better with inflation than an exploding Universe containing massive objects from start. The actual model suggests that the dark energy equals the kinetic energy of the dark mass. This energy, which was neglected together with the structure in Equation (6), is estimated to. During say 3/4 of the initial relaxation, where almost massless quarks propagate almost freely, the travelling wave velocity k should approach the velocity of light (c = 1). In the remaining 1/4 more plasma-like part, where most mass should emerge but quarks can still move rather freely, the wave is assumed to slow down to the velocity of sound [25] . The average velocity then becomes, hence F(k) = 2.340, which with m_d = 0.259 yields a dark energy e_d ≈ 0.606.

Similar to the “atomistic” theory of matter and electricity proposed by Einstein and Rosen [26] , this model reduces the warping of space-time implied by the Schwarzschild metric factor (1 - 2GM/rc²), but in a different manner. When energy increases, the chemical non-equilibrium model dynamics goes backwards. M then becomes replaced by, and vanishes with φ(t) (Figure 2(b)) for t ® -t₀ according to Equation (15), R > 0 being a factor to be determined. This also reduces the amplitude of gravitational waves from black hole events, such as formation and coalesce of black holes, making such waves extremely hard to detect [27] .

When mass vanishes, the dust-like particles accelerate to the velocity of light and their clocks stop ticking, at least until they become rematerialized. The question is whether the negative gravitation and negative energy are sufficient to permit rematerialized particles to return to our own world sheet from the interior of black holes [26] . The existence of relativistic jets seems to support such a possibility, but it is also a question whether these jets are driven by the accretion disk [28] [29] , or by the black hole itself. However, it is doubtful that tidal forces outside or at the event horizon can drive Equation (1) backward and trigger pair-creation.

Clearly, this chemical non-equilibrium interaction is but an attempt to model what actually takes place in the real Universe, however, it seems to be first to go beyond the grand canonical ensemble in a system containing strong spatial correlations, and it also seems to work reasonably well. Observe that transport theories have not succeeded to solve this type of chemical non-equilibrium problem, and have thus not solved the problem for lattice QCD [4] . The actual model, which starts with massless particles, also provides a novel aspect on the mysterious wave-particle duality. After symmetry breakdown, both minima of the double-well potential―one corresponding to the de Broglie/Schrödinger wave nature of electrons without mass and one corresponding to electrons with mass (Figure 2(d))―have become equally physically probable. Hence, since the massless wave, which coexists with the corresponding massive particle, allows non-local interactions by infinite wavelength quanta, which are in principle non-loca- lizable, this might resolve some of the worst controversies between quantum mechanics and relativity, such as signals propagating faster than light.

It is also interesting to compare the -sea of the actual model with the Dirac-sea [30] , which used ideas from condensed matter hole-theory. However, there was then no acute reason to go further and study condensed matter properties and collective phenomena of vacuum, because QED admitted massive particles already from start, and so did QCD.

Acknowledgements

I thank Ludvig Faddeev for stimulating discussions on this matter many years ago at CERN, where I first got the idea for the model.

Cite this paper

Matsson, L. (2016) Higgs-Like Mechanism by Confinement of Quarks in a Chemical Non-Equilibrium Mo- del. World Journal of Mechanics, 6, 441-455. http://dx.doi.org/10.4236/wjm.2016.611031

References