Received 20 January 2016; accepted 26 March 2016; published 29 March 2016

ABSTRACT

Relativity theory formulation is proposed, based not on the axiomatic postulation of its main principles but on their inference out of a thought experiment. With this approach, the experimentally observed independence of the speed of light from the motion of source and observer is a necessary consequence of the finiteness of propagation speed of all kinds of information. The mechanism of relativistic effects origination is described; the formulas of Lorentz transformations, Doppler quadratic effect, electromagnetic interaction and centrifugal force of inertia are derived.

Keywords:

The Principle of Relativity, The Measurement Process, Lorentz Group, Doppler Effect, Mach’s Principle

Judgements of any theory concern the correlations between solid bodies (coordinate systems), clocks and electromagnetic processes. Insufficient understanding of this fact is the root of those difficulties which the electrodynamics of the moving bodies has to overcome now.

Albert Einstein

1. Introduction

The task which at the end of XIX century was set to electrodynamics of the moving bodies by the accumulated experimental data was solved by Einstein: Galilean relativity principle was expanded; along with the mechanical phenomena it now included electrodynamic ones. This required postulating the independence of the speed of light in vacuum from the motion of both the source and the observer―otherwise the experimental indistinguishability of the inertial reference systems was unattainable. Over the past 110 years, the huge database of more and more accurate experimental data unequivocally confirmed both this postulate by itself and conclusions of the theory.

In the theory of relativity the principle of the light speed constancy is introduced as the axiom; purely mathematical following to this axiom necessarily leads to Lorentz transformations. Physical mechanism that provides for the validity of the light speed constancy, i.e. the analysis of the measurement process, is beyond the theoretical framework.

In the present article, exactly such analysis is carried out. Consideration of thought experiments involving measurement of segment lengths and time intervals in inertial reference systems moving relative to each other allows one to build a logically closed scheme. Out of this scheme, the postulates of the relativity theory are derived not as absolute mathematical principles, but as a result of experiments that are carried out with currently achievable accuracy.

The thought experiments proposed in this article are designed according to the same scheme. The basis of this scheme is as follows. We start with a hypothetical reference system in which the information on any physical event propagates in vacuum in all directions with the same speed. An observer located in this initial reference system―also hypothetical―explores other uniformly moving reference systems. At that he initially uses the line of reasoning as if he possessed the ability to obtain information on the physical events without delay, i.e. instantly. Observers in the moving systems perform clock synchronization and information acquisition using those real signals which are propagated isotropically in the initial reference system.

The task is to describe the results of experiments performed by the moving observers, specifically the measurement of segment lengths and time intervals.

* * *

Since rigorous tracking of all the mathematical calculations requires significant time, their purely computational parts were moved to the appendixes.

2. Kinematics

Absolute (Abs) will be called the imaginary observer who is situated in the initial reference system and is able to receive the information without delay. The real method of infinitely fast transmission of information for such theoretical analysis is not necessary―this is exclusively the imaginary experiment. In further consideration the need in such observer will be no longer relevant and imaginary experiments will be related to the reality.

Further on, there are two reference systems moving uniformly relative to the initial one. In each of them there is the resting observer, who uses the light signals. Light signals are propagated relative to the initial reference system in all directions with the speed of c. This is the only one initial assumption. Out of it there will be derived the properties of light, observed in the other inertial reference systems.

2.1. Lengths of the Moving Segments

Let’s assume that from the viewpoint of Abs the situation is as follows: at rest the lengths of two segments are equal. Since Abs receives the signals without delay (infinitely fast), then for him these segments will be of equal length in the motion as well. The segments move relative to the initial system with the speeds and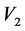, the observer is located in the middle of each segment.

System E “overtakes” system F, at that the contact of A and B points and A' and B' points from the viewpoint of Abs occurs simultaneously (Figure 1). Abs observer sees: the signal from the contact of B and B' points reached F observer prior to the signal from A and A' contact by

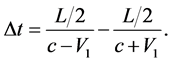
This means that from the point of view of the F observer, who synchronizes the clock by light signals and uses Einstein’s definition of simultaneity concept of the distinct located events, the A'B' segment in E system is longer than the AB segment in the F system.

Detailed calculations―see Appendix 1.

As the result we have the following: in relation to the length transformation of moving segment in comparison to its length at rest, there is the asymmetry (depending on whether the observer is in the “overtaking” or “lagging” reference system, the length either increases or decreases). On the contrary, in the case of comparing the segment

lengths that are already in motion, with the segments arranged in the laboratory reference system, there is the complete symmetry: if from the point of view of the laboratory reference system, some “B” segment, located in the moving system, is equal to the “A” segment located in the laboratory system, then from the point of view of the moving system, the “A” segment is shorter than the “B” segment, and the reduction factor is equal to

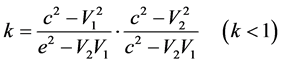―this is true “in any direction”. (1)

Important remark.

Direct experimental comparison of the length of the solid body at rest with its length in the motion would have required technically unreachable measurement accuracy and speed. Said is also true with the respect to the second (symmetrical) statement, however, consequences from it, derived below (and also symmetrical), are available for such verification.

In reality, the observed asymmetry of “overtaking” and “lagging” reference systems can prove itself in the electrodynamic experiment. Such experiment would allow to answer the question whether the proposed here logical constructions are purely speculative or they are related to the physical reality.

See details in paragraph 6.

2.2. Light Speed

Let us find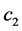―the longitudinal light speed measured in the E reference system. Let the light goes from A' to B'. From the Abs point of view, A' and B' clocks, which are synchronized in E system, are not synchronous: A' clock

are fast in respect to B' clock by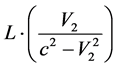. (Difference of time intervals expended by the synchronizing light signal to cover the distance 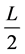from point E―center of A'B' segment―to A' and B' points: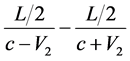.) So, the time of light advancing of the length L in the E system, measured by the clock in E, will be less than:

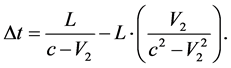
We get:

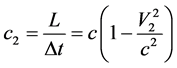(2)

(Of course, for the light impulse that moves from B' to A', we get the same result.)

Analogous, the light speed measured in the F is equal

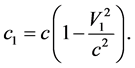(3)

2.3. Relative Velocities of the Reference System’s Motion

Let us find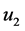―the speed of F system measured in the E system. Considering that the clock A' with respect to the clock B' is fast by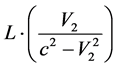, the time, within which F point flies over all the L length in the E reference system, will be measured by E observer “with error”: F flies to the left, therefore the time will be longer:

;

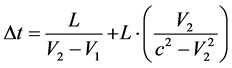Speed of F system measured in E system:

, where (4)

Exactly the same reasoning lead to the formula for the speed of E system, measured by F observer:

, where (5)

(at we get. True.)

Assuming the value of one of the speeds equal to zero, we get: the real observer using the light signals, located in the initial reference system, when measuring the length of the moving segment, the speed of the moving system or light speed, will obtain the same result as the hypothetical absolute Abs observer, i.e. the “true” value. Another could not happen.

Important remark.

If any of observers measure the speed of another observer using as the measurement unit the light speed obtained by himself, their results will be identical:

;―relative speed of reference systems in SRT.

Analogous statement is correct for any kinematic measurements carried out in one of the uniformly moving reference systems, since the observer in each reference system uses his own standards of length and time. That is―“own” light speed.

To find out the asymmetry having the ideal measurement instruments, the observers could in one of two cases. Variant the first, theoretical: the both moving systems remain to be inertial, in each of them there is the observer and these observers have the agreement on the standards of “meter” and “second” (for example, on the basis of the specific atomic standard of frequency and wave length). Variant the second, real: the observer is located in the reference system which is not strictly inertial, for example, it moves along the circumference. This will allow him to compare the measurement results, for example, the light speed in various time moments. At the real speeds and dimensions of the reference systems, as will be shown below, in the both cases the currently unattainable precision would be needed for such measurements.

2.4. Time Terms

The scheme with two reference systems and the absolute observer (Figure 1). The first case: two events are one- place-located in the E reference system. Let these events―contact of the E observer with the origin and the end of AB segment, located in F (its length at rest―i.e., from F viewpoint―is equal L). From E viewpoint the length of this

segment:. The speed of F system from the E viewpoint is equal. Therefore, the time term that splits the considered events, from E viewpoint is equal:

(From Abs viewpoint this time term will be the same, as those for the “light” observer located in the initial reference system, no “transformations” are needed: when measurement of moving segment lengths and time terms, he obtains the “true” results. When change in formulas of the value for the zero value, just such result is obtained.)

The same two events from F viewpoint are divided by time

;

Hence:

; (6)

(The events are one-place-located in the “overtaking” reference system E.)

Formula for transformation of the time term, splitting the events that are one-place-located in the F system, is derived in the similar way. We will obtain it, however, in another way which is more obvious and does not require the use of the previously derived formulas for the length and speed. From observer viewpoint in the initial ref-

erence system, the time of flight by F point of the A'B' segment in the E system is equal. The F observer by himself, within whose system two events take place, will get the same result:. From E system viewpoint the time of F point passing by A'B' segment is longer, than so far as, from the viewpoint of the initial reference system, the A' clock are fast relative to B' clock, i.e. for:

Therefore:

; (7)

(Events are one-place-located in the “lagging” reference system F.)

2.5. Velocity Addition Theorem

Three reference systems designated as “1”, “2” and “3” move along a straight line from the viewpoint of initial reference system and their velocities measured by the observer in it, are equal, and accordingly (Figure 2). At that the speed of number 2 system measured by the observer in number 1 system is equal u, and “number 3” speed measured by “number 2”, is equal w.

Calculations―see Appendix 2.

We get:

(8)

(9)

Important remark.

Resulting speed, obtained when addition of two speeds, each of which is less than C, is always less than C. The reason of this is obvious: the reference system moves with the velocity not exceeding―by condition―the light speed, and the observers from another systems measure the speed of its motion; it is understood that obtained by them results do not exceed the light speed in their reference systems.

If in the nature there existed available for observation body having the faster than light velocity, then in the point of “finish” it would be earlier than the light signal emitted simultaneously with it. Under conditions of clock synchronization, the time term that such body would expend to overpass the specified segment, pure formally would be negative. Here is no causality violation.

Considered correlations do not “prohibit” the existence of the velocity that exceeds С. No physical phenomenon (inertia growth with velocity growth) is behind these correlations, the matter is only in the finiteness of the rate of information transmission.

2.6. Group Properties of Obtained Transformations

The validity of the mandatory property of the obtained correlations, without which they could not be considered closed, should be verified. Just the consequent application of transformations (whether it is the transformation of segment length, time term, speed or application of the “velocity addition” law) during the transition from one system to another, and from it, in its turn, to the third, should give the same results, that when transition from the first reference system directly to the “number three” reference system. In other words, our transformations should form the group.

In the simplest case, this looks as following.

Let the velocities of the reference systems with numbers from “1” to “4”, measured in the laboratory reference system are equal, correspondingly, from to, and the relative velocities measured in each of the systems are equal u, w and q, as it is shown in Figure 3. Let obtain the velocity value by two methods, using Formula (8). As in case with the Einstein formula of the velocity addition, the results are the same. However, the difference is vital. Einstein formula of the velocity addition, as the whole group of Lorentz transformations, is obtained from the axiomatic requirement of light speed constancy at its measurement in any inertial reference system. Pure ma- thematical succession to the specified axiom leads to such form of velocity addition law. Contrary, the derived here regularities are obtained as the result of measurement process consideration. In particular, there actually

happens no real “velocity addition” and in spite of the obvious resembling of Formula (9) and Einstein formula of the velocity addition, the key point of described by this formula laws is different.

2.7. Accordance with Reality

Let show that obtained within the described above theoretical scheme, physical laws accord to the axiom system formulated by Einstein.

Observers, acting under the accepted conditions, when carrying out measurements of the light speed and relative speed of the uniformly moving systems with the available for them accuracy (i.e., carrying out those measurements that are actually available), will receive the results which lead them to the following hypothesis: indistinguishability of the uniformly moving reference systems, i.e. relativity principle, covering any experiments including the experiments with light; and therefore―the principle of light speed constancy: at the measurement it is obtained equal regardless of source or observer motion.

Within the framework of the proposed hypothesis, it is possible to carry out the following theoretical reason- ing.

Having excluded the non-existent “absolute” observer, let us consider the new actually admissible experiment.

Light speed from the viewpoint of E reference system is equal c. By E observer located in the center of motionless segment with the length of L, with the velocity u flies the segment, the ends of which simultaneously contact the ends of segment in the E system (the light signals from the contacts come to the segment center at one and the same moment). The picture from the viewpoint of the observer in E system is: (Figure 4)

E observer argues. F point moves to the left, i.e., towards the signal from the contact of left ends and moving away from the signal from the right. Signals, that come to the E point simultaneously, will come to the F point with variable timing. This discrepancy measured by the E observer is equal

.

From the fact, that the signal from left comes to the F observer earlier than the signal from right (this fact is absolute), F observer by himself, who also reasons in the framework of the accepted axiom, may make the only one conclusion: the segment in the moving E system is shorter than the segment in his system. From the viewpoint of the F reference system, wherein the clock is synchronized by the light pulses, the picture looks like this: (Figure 5)

(To carry out all these reasoning, the real observer situated in the F system is not needed―the objective fact of the variable timing of signal coming in the F system center is enough, in other respects the E observer may theoretically reason.)

Continuing to form up the logics on the hypothesis that all the uniformly moving reference systems are equivalent, we have now to find out such transformations for the segment lengths and time terms, which in the framework of this axiomatic would consistently describe the existing experimental situation: the observer in one of the systems sees, that “resting” and “moving” segments are equal, and the observer in another system―that the length of the same segments are different: “moving” segment is shorter, than the segment resting in his reference system. At such setting up, the task has the single solution: the segment which length at the rest is equal to L, being

measured in motion, has smaller dilatational length:; (), where u―the motion speed of this segment, c―the light speed: the function of the length transformation cannot depend on any other parameters. Our

axiom system comprises the statement on the space uniformity (also experimentally confirmed), therefore the linear dependence was chosen.

Following the same logics, let us consider two events, one-place-located in the F reference system. If between them, according to the F clock, passed the time, then, according to E clock, between the same events passed the longer time:.

It is proved in the following way: events, that are one-place-located in F, leave on the segment, located in E system, the marks, the distance between which from the F viewpoint is equal. Since these marks limit the segment that is motionless in the E system, then its length, measured by the F observer, is shorter than the very same measured by E observer by times. That is, its length in the E system is equal. And since the motion speed of the point, located in the F system, wherein these two events have taken place, measured by E, is equal u, therefore, the time term, which this point would have spent to overpass this segment is equal.

Applying the obtained correlation to the discrepancy time between two events, which are one-place- located in the F reference system, we get:.

Further, form the F observer viewpoint the segment in the E system is shorter than the segment in his system by. At that the E system length from the F viewpoint is equal, i.e. the segment length in the F system from the viewpoint of the F system itself is equal:

At the same time, the segment length in F system from the viewpoint of E system is equal L, and length ratio “(segment length in F from viewpoint of F)/(segment length in F from the viewpoint of E)”―this is just. We apply to:

, from which.

Thus, remaining in the framework of the accepted axiomatic, we obtain the Lorentz transformations. As it was shown, there is no symmetry in the scheme with the initial reference system, in those systems, where clock are synchronized by the light signals, another picture is observed: for the reference system that moves with respect to the initial one with the speed, there takes place the length increase of the segment which moves with the speed, compared to its length at the rest, otherwise there takes place the length decrease. However, the direct experimental verification of theses correlations at the available measurement accuracy is impossible. And the experiment for comparison of the lengths of two different segments, one of which moves (in contrast to comparison of the length of one and the same segment in motion and at rest) gives the symmetrical results at any measurement accuracy.

Let us apply to this experiment the statement on reduction of moving segment length in comparison to its length at rest by times―and we will obtain the following. E and F reference systems move with the velocities and (the scheme in Figure 1). From the E viewpoint some segment, located in the F system, is equal to the segment in the E system, having the length L. In the framework of the hypothesis about the length reduction this means, that at rest its length (F observer measuring the length of “his” segment, would obtain the value). At the same time, from Formula (1) it is known that the direct measurement (without any axiomatic constructions) will show the following: from the viewpoint of the F observer, the segment located in E, is shorter than “his own” with the reduction factor k, i.e. its segment length, located in E from the viewpoint of F is equal. But once from the E viewpoint the segment in the E system has the length L, then its length measured by the F

observer should be equal. Hence:, i.e.

(10)

Both this result and measurement results of the relative motion speed of the systems and light speed do not contrary to the hypothesis on that all uniformly moving reference systems are equivalent, if these measurements are carried out in the systems, the speed of which relative to the initial system is of the order of one thousandth of the light speed, and the measurement accuracy is insufficient to notice the differences of the order of one part per million. Let us show this. To make the approximate estimate, let us consider the example with the specific speed

values of the both reference systems relative to the initial one. Let the velocities of two observers and relative to the initial reference system are of the order of, and their relative speed is.

For such velocities we obtain the difference of the experimental results from those that STR predicts―not more than in the sixth decimal place (calculations―see Appendix 3). This calculation relates not only to the length reduction, but to the light speed measurements and relative motion speed of the reference systems.

2.8. Transformation of Coordinates and Time

Let us derive the transformation formulas when transition from one uniformly moving reference system to another:

Let from the viewpoint of the initial reference system the velocities of systems K and are co-directional and are equal and correspondingly, at that (“shaded” reference system―overtaking) (Figure 6).

From the viewpoint of K system, the segment length that is motionless in the system, is equal, where―the speed of system, measured from the K system. The length of this segment when measuring from the system:

(11)

The segment of length x, located in the K system, form the viewpoint of has the length. The point with coordinate in the system “started” in the “zero” time moment according to the clock, and by the time according to the clock reached the point, this means, that according to the clock had passed the time

(12)

From Formulas (4) and (5):

(13)

(14)

Inserting (13) and (14) into (11) and (12), we get the transformations of time and coordinates at the transition from one uniformly moving reference system―to another (in the simplest case, of motion along one line in the initial reference system):

(15)

(16)

(Direct verification of the group properties of this transformation for the simplest special case is as follows: we consider three reference systems moving in the initial system along the single line with velocities, and.

Passing from system 1 to the system 3 by two methods―“in chain order” and “directly”, we obtain the equal expressions for transformation of coordinate and time.)

In matrix form:

(17)

Matrix in this expression may be written in the form of the product:

where―relative speed of the reference systems in SRT.

If for the reference system having the absolute velocity, instead of the used time and coordinate, introduce the new:

, (18а)

And, similarly, for the reference system having the absolute velocity:

, (18b)

then transformation will be as follows

(19)

that coincides with Lorentz transformation form.

In the new coordinates the kinematic parameters take on the symmetry property.

Replacing in Formulas (13) and (14) time t and coordinate x by and, we obtain the formulas for relative velocities:

;

(relative velocity of reference systems in SRT).

The light speed, measured in each of the moving reference systems in the new coordinates, is also equal. From Formula (3): It means,. Similarly,.

It is understood, that with given distinguished reference system, there could not be symmetry in all dimensions. Asymmetry remains immutable when comparing the length of the moving segment with its own length at the rest: depending on that whether the observer is in “overtaking” or “lagging” reference system, the length either increases or decreases. Let us repeat that: the experimental verification of this statement would demand the inaccessible precision of length and time measurement. The consequences from that are symmetrical.

If such verification would become technically possible, then the differences in the direct measurement results in the new coordinates from the calculations, carried out according to SRT formulas, at the above velocities of the reference systems would be of the order of. In the case of the comparison of lengths of the segments, which are in motion, with the segments located in the laboratory reference system, in the new coordinates, we obtain, as could be expected, the complete symmetry:

Since, then, where k―the factor from Formula (1). Which means, in the Formula (10):, i.e. in the new coordinates, the result will be not approximate, but precise.

So, from the group viewpoint the transformation (17) is the Lorentz transformation, written not in the Lorentz coordinates, but in the coordinates related to Lorentz formulas wherein the reference system absolute velocity is included.

Ordinary four-dimensional integral, invariant relating to Lorentz transformations would not be invariant relating to transformations (15). Instead of it, invariant is the four-dimensional integral, determined as

i.e.:

Usually Lorentz coordinates are more convenient, since they do not require the dedicated reference system, and the interval in it is simpler, however, the proposed coordinates explain, how appears the Lorentz group in the Minkowsky space.

3. Dynamics. Dependence of the Inert Mass of the Moving Body on Its Speed

Let us take the imaginary experiment, similar to those, that was proposed by Einstein in the article “Whether inertia of the body depends on the energy contained in it” [1] [2] .

Let certain body, moving relatively to the reference system, wherein the observer is located, at one and the same moment emits two identical light “portions” in the opposite directions. In the reference system, initially connected with the considered body, it is motionless both prior to emission and after it (requirement of the symmetry). Let the energy of each of two emitted “portions” in this reference system is equal. In the laboratory reference system, body prior and after emission moves with the speed V, and the energies of the emitted light “portions”, measured in this systems, will be equal (the light, emitted “counter-motion” of the body) and (“along the motion”).

In order to write for this case the law of conservation of energy, the work of the recoil force, done during the emission act:; should be considered. Here―energy, measured in the laboratory reference system, which would have the light emitted by the body, if there were no recoil. In the case, when the considered hypothetical “portions” of the electro-magnetic radiation are the light quanta, the value―if the

difference between energy levels of the moving atom prior to emission and after it, measured in the laboratory reference system. For this task it does not matter by what law the value depends on the value (i.e. on difference between Bohr atomic energy levels at rest) and on the velocity V.

When considering in the laboratory reference system for each of the emitted light “portions”, the work of recoil is equal to the product of the impulse, taken away by the “portion”, and the emitting body motion speed. At the same time it is known that the impulse of any limited “portion” of the electro-magnetic radiation is equal to the

energy of this “portion”, divided by the light speed:;. Thus,. That is. In the similar way:. Therefore, from the viewpoint of the initial reference system, all the emitted energy:

Significant remark.

Already by itself, the requirement for observation of the conservation laws in the necessary way leads to the dependence of the body mass on its velocity. As a matter of fact, each of the emitted light “portions” has both the energy and the impulse (experimental fact which is undisputable). As the result of the symmetrical emission of two light “portions”, the speed of the emitting body cannot change. Therefore, if we want the emitting body impulse to change by the value, equal to the difference of impulses of the emission “portions”, then it would be needed to require to change this body mass. Just this logic used Einstein. Having added to this logic the Lorentz transformations, whereof is derived the formula of light “portion” energy transformation from one reference system to another, Einstein obtained the approximate formula of the dependence of body mass on its speed. Let us show that there is no need to use the Lorentz transformation, the fact is enough that energy and impulse of the

electro-magnetic radiation are correlated by ratio.

So, let us write the law of conservation of impulse for the considered imaginary experiment:

Hence:

.

And we obtain:

change in body mass at the light emission is equal to emitted energy, divided by the square of the light speed. This is not approximate, but exact formula. Since while deriving more or less arbitrary assumptions were used, namely, the laws of conservation of energy and impulse, that are known from the mechanics, were expanded to the interaction of the solid body and electromagnetic radiation, besides, the work of recoil force at the light emission was calculated with the use of law, known also from the mechanics of solid bodies, the obtained formula needs to be experimentally verified. More exactly, would have needed, if over 110 year, passed since the time of Einstein study publication, this law would not be many times proved on practice. Also, the more strong assertion happened to be true: the body mass may be entirely transformed in the energy of electromagnetic radiation, as if the body is “made from light”: and in this case the ratio remains to be true. Einstein assumption, that electromagnetic radiation transfers the mass between bodies, is true. However, this physical law does not have the

relation to SRT axiomatic: that fact is enough, that the condition is met for light.

4. Doppler Quadratic Effect

Formula for Doppler quadratic effect, obtained by Einstein, repeatedly and with high accuracy is confirmed by the experiment―beginning from the experiment of Ives and Stilwell in 1938, in which the radiation of hydrogen atoms was studied [3] . To measure the frequency of light emitted in the direction that is strictly perpendicular to the atom motion velocity is not possible, therefore in all the experiments of this type the radiation frequency “along the motion” of atom and the “counter-motion” radiation frequency are compared with the frequency emitted by the same atom “at rest.”

To form up the theoretical model of the Doppler effect, we will proceed from the quantum nature of emission (to consider certain excited hydrogen atoms, the emission spectrum of which in this case is strictly line, as the sources of continuous electromagnetic waves there are no grounds). Relativistic theory of Doppler quadratic effect first proposed E. Schrödinger in 1922 in his article “The Doppler effect and Bohr postulates for the emitted frequencies” [4] . This theory is based not only on the Bohr quantum concepts light emission by atom, but also on Einstein’s formula for the relativistic transformation of the rest mass.

From imaginary experiment with the simultaneous symmetrical emission of two light “portions” in the opposite directions let us proceed to the description of actual experiment, in which the moving atom emits the light quantum with the transition from one Bohr energy level to another. We consider the case of light emission in the direction of atom motion.

In the new designations:, where―atom rest energy,―its rest mass. Then the total energy of atom in motion:. Further on for simplicity of writing, we

suppress index “0” and will designate the rest energy as ordinary “E”. Let the Bohr energy levels of atom at rest are and, at that (if there would not be recoil appearing at the emission, the initially resting atom would emit the light quantum with the energy of).

Radiation of the moving atom, the law of conservation of energy:

Here and―the atom velocities prior and after the emission correspondingly (their difference―is also the recoil consequence). The observer is located in the reference system, wherein the velocity of electromagnetic radiation expansion in vacuum is isotropic and equal c.

Detailed calculations―see Appendix 4.

As a result we have: the expression for the light frequency, measured by the observer in the initial reference system, under condition, that the light source moves relative to it with the speed V:

(20a)

For the case, when the light is emitted in the direction that is opposite to the source velocity:

(20b)

In the experiment of Ives and Stilwell, as well as in the all consequent experiments, the formula of relativistic Doppler effect for the moving source was verified:

All the experimenters, during calculations, accepted the approximation, that at and (in the experiments the wave lengths are compared which are emitted exactly in this two directions) leads to the Formulas (20a) and (20b).

* * *

So, the proposed approach, based on the analysis of information communication by the light signals, allows not only obviously obtain the Lorentz group (and thereby all the kinematic relativistic effects), but also strictly describe such key experiment, as the experiment of Ives and Stilwell.

5. Magnetic Action of the Electric Current

To describe the interaction of the uniformly moving charges and the material point that carries the electric charge (and also moves uniformly), we use the following model of the Coulomb interaction. The charge carriers that move in the conductor with current (we take into consideration only the drift velocity, assuming the thermal motion to be average zero) create at the point, where the test charge is located, the intensity, and the charge interacts exactly with this integrated intensity. If at that the test the charge is not motionless relative to the charges of conductor, then, to learn how the force that acts on it has changed in comparison with the force at rest, it is enough to know the law, which describes the dependence of the force, that acts on the charge at the point with known intensity, on the motion speed of this charge. To obtain this law, we use the model in which modulus of the electric field intensity is characterized by the density of “lines of force” at this point, and its direction-a tangent to these lines. With all the conditionality of this description, it not only agrees with the inverse square law for the three- dimensional space, but turns out to be sufficiently adequate, in particular, at the transition from the classical to the relativistic description of the electric field. In the framework of axiomatic of special theory of relativity, assuming that the moving object dimension reduces in the motion direction in comparison with the corresponding dimension

at rest in times and considering the number of lines of force per normal unit of area, as the proportional characteristic of the intensity in this point, we obtain the transformation of Coulomb law for the field of moving point charge:

where―the angle between the motion direction and radius-vector in the reference system of the observer. In two extreme cases this expression becomes enough obvious. Let in the reference system, wherein the creating field charge q is motionless, acts the Coulomb law. The observer which moves through the filed point

with velocity V, measuring the “denseness” of lines per unit of the normal area, will obtain their “densification” in comparison with “denseness” at rest. This relativistic intensity increase will be maximum in the case, when the

lines of intensity are perpendicular to the velocity, (thus, the velocity is parallel to the plane that is normal

to the intensity vector, and “area” reduces in the direction of velocity at the constant number of crossing lines); the radius-vector is also perpendicular to the velocity and its length, measured in both reference system, is equal:

. Minimum intensity is obtained in the direction that is parallel to the velocity,; in this case “denseness” is the same when measuring in each of the systems, and the radius-vector length from observer viewpoint maximum decreases in comparison with its length from the viewpoint of the system wherein the field source rests: . The last formula does not mean that moving charge field “flattens”

in the direction of motion. The intensity in this point when measuring it by resting body and body, which moves in parallel to the intensity vector, is equal; different turns to be only the distance from this point to the field source, measured in the different reference systems.

Let us apply the analogous approach to describe the action of direct current on the moving charge using the above obtained laws. Since the information about the change of positions of the charged bodies is transmitted at the speed of light, we choose the light signals as the “synchronizing” signals. Let the conductor, whereby flows the constant current, is located in the initial reference system (therein is the real, and not only observed with some accuracy, in the framework of the agreement on the clock synchronization by light, symmetry in the propagation of the light signals).

Let’s start with the simplest case. Let the negative test charge (relatively-electron) moves at the distance of R away from the conductor with current with the velocity V of the same value and direction, as the charge carriers in the wire. In the reference system, wherein these charges are motionless, the Coulomb repulsive force is easily calculated. Let in the laboratory reference system, per unit of wire is necessary the charge amount of free carriers s (C/m). Then, when the drift velocity V (m/s), the current value is (А). Since at the measurement by observer located in the initial reference system (wherein the conductor is motionless), the lengths of the moving objects turn to be the same as at the rest, carrier’s charge per unit of length in the moving reference system is s too. From the side of conductor free electrons on the electron, flying with them by “parallel course” at the distance R, acts the repulsion force. Let us calculate it (Figure 7).

Coulomb force:. In the projection onto the perpendicular to conductor:. Repulsive force from electrons of the whole conductor:

.

Further, the attractive force from the side of conductor ions acts on the electron that flies in parallel to the conductor. If the test particle was motionless relative to the conductor, i.e. in the initial reference system, then from its viewpoint the length of the segment, which moves together with the charge carriers in the conductor, would be the same as it was at rest. This means, that Coulomb forces acting on it from the side of moving and resting charges would be equal and would compensate each other. In other words, no forces act on the motionless charge from the side of current-carrying wire (in SRT this is not the case―therein everything is symmetrical). If the test charge moves with respect to the initial system, then comes into action the Formula (1.2) from Appendix 1 for

“overtaking” reference system at: from the viewpoint of the moving system the segment length located in the initial reference system:. Correspondingly, the Coulomb interaction also increases: the force

which acts on the moving electron from the side of resting conductor’s ions

Electron’s drift velocity in the conductor―of the order of mm/s, therefore with the vast precision it can be assumed. Subtracting, two forces (from the side of electrons and from the side of ions) result in the attractive force, simply stated―Lorentz force: (co-directional currents are attracted). Taking into account that in Coulomb law, and, we get:. (As it is known, magnetic field induction of the endless direct conductor at the distance R away from it; Lorentz force in case of the right angle between the velocity and induction vector.)

Let us consider more general case: the velocity of the test particle u as before is parallel to the conductor, but is not equal to the drift velocity V of electrons in the conductor. Interaction of the test charge with conductor ions, as before, is described by the formula obtained above:.

Let. Formula (1.2) in Appendix 1 (observation is carried out from the “overtaking” reference system). Velocity in the formula―it is V in our case, velocity―is u. Then the increase factor of intensity, which is perpendicular to the velocity, in comparison with the rest, in this case is equal

.

Correspondingly,. Total force:. And we get:.

Calculations for the other correlations of u and V―see Appendix 5.

So, in the framework of the derived above laws, Lorentz force in the all interaction variants of the charged body and conductor with current:

6. Possibility of Experimental Validation

As it was said in the item 2.1, the asymmetry of “overtaking” and “lagging” reference systems should approve itself in the electrodynamic experiment. Such experiment would allow replying to the question, whether proposed logical constructions are pure mental or they have relevance to the physical reality.

Let us consider the interaction of the current-carrying conductor, that moves with the velocity w relative to the initial reference system, with the particle, which motionless relative to the conductor. At that the electrons in conductor move in the same direction relative to the initial reference system with the velocity.

For observer located in the F system (in notations of Figure 1), the length of the segment located in E system of the drifting electrons, in comparison with the length of the same segment at rest, will be increased in accordance to

Formula (1.1) from Appendix 1―For observation from the “lagging” reference system:. This means that the charge density of moving electrons, measured by F observer, will decrease:;―charge density at rest. The expression within brackets is <1.

(Independence of the charge value from the reference system we take up as the experimental fact.)

The test charge is positive; moving electrons in the conductor attract it, non-compensated ions of the conductor―repulse it with the force which is determined by the initial charge density:

The force from the ion side is greater; the resultant force―repulsion: the conductor with current at such positioning of the relative velocities should conduct itself as positively charged body. Summing the effect of the drifting electrons and ions, we get the specific charge of such „charged” thread―from the F observer viewpoint:

The value represents the drift velocity of electrons in the conductor (measured by the “Abs” observer), i.e. the repulsive force of the resting positive charge from the conductor is directly proportional to the current value. If the test charge and the conductor with current are situated in the initial reference system, i.e., then there is no interaction of the charge with the current, what we observe in the conventional laboratory conditions.

So, if the proposed model corresponds to the reality, then outside the initial reference system the motionless positive charge must feel the repulsion from the conductor with current.

SRT requires in this experiment―as in all others―the complete symmetry: location of the experimental installation in any inertial reference system should not affect the experimental results.

We will consider that the initial reference system―is those, wherein the cosmic microwave background radiation is isotropic. Then the interaction of the motionless charge with the current will be maximal in the case, when the electron drift in the conductor is co-directed with the Earth motion relative to the cosmic microwave background and will become zero, if the conductor is perpendicular to this direction.

Let us give the estimate of the expected interaction force for the real reachable values of the test charge, intensity of current value and distances. Let velocity w of the laboratory reference system relative to the initial one is

of the order of 400 km/s, and the drift velocity of electrons in the conductor is of the order of 5 mm/s. Then.

At the current of the order of 1000 А the specific charge of the drifting electrons per the unit of the conductor length is of the order of C/m. If the conductor represent the thin plate, wherein the current density is everywhere the same, then at the plate length of 25 sm and the width of 4 sm this gives the specific charge per unit of area C/m². When performing the experiment under conditions of the initial reference system, the whole charge of the moving electrons is compensated by the equal charge of the conductor ions. Under conditions of the motion relative to the initial system the uncompensated specific charge of ions, evaluative, is of the order of C/m². When the described conditions are satisfied (positioning of the conductor with current in such a way, that electrons in it would drift in the same direction where the Earth moves relatively to the cosmic microwave background), such plate with current must interact with the test charge in the same way, as if it were charged up to the calculated density of charge. If to use, as the test charge, the plate, to which the constant voltage of the order of 10 kV is applied, located at the distance of the order of 1 mm from the current-carrying plate, then at the same area of the plates the expected maximal force of interaction is―of the order of 10⁻³ N. In the case of positioning of the experimental installation on the Earth and at the precise as possible orientation of the current-carrying plate in the direction of the Earth motion relatively to the cosmic microwave background, one might expect to obtain the force of plate’s interaction which differs from the maximum at most by two orders, i.e. such as would correspond to the value of velocity of the order of units km/s. In other words, the torsion balance, confidently responding to the interaction force of the order of 10⁻⁵ N, should be admitted acceptable for the test experiment. This is―the interaction force of the plates located at the distance of 1 mm at the potential difference between them of 15 V. Such response is easily achievable.

* * *

Proposed approach provides for the opportunity on the basis of the finiteness of the signal propagation velocity to obtain the following: in the rotating non-inertial reference system the centrifugal force of inertia is the result of gravitational interaction of the body with all the bodies of the Universe, which corresponds to Mach’s principle, that explains the equivalence of inertial and gravitational mass. Let us show it.

7. Mach’s Principle

Reasoning in this section are formed up on the basis of the same logic, which was applied above, with those difference, that the matter concerns the propagation in vacuum of the information on arrangement of the gravitating masses, but not the electric charges. At that it is supposed that the velocity of this propagation is also equal to c.

Let the E observer is situated in the system that is rotating with the constant angular velocity relative to motionless Universe that acts the part of the initial reference system. Circle radius, along which moves the E observer, is equal a.

Calculations―see Appendix 6.

So, at the uniform distribution of, for example, the charge by the spherical volume, on the material point which moves along the circle with radius a with the angular speed, acts the force directed centrifugally, as the result of the interaction of this material point with the whole volume contained in the sphere, and the asymmetry caused by the signal lag in the reference system differing from the initial one.

Let us apply the obtained result to the sphere with radius with the uniform distribution by volume of the charge or the gravitating mass.

Calculations―see Appendix 7.

Integrating the obtained expression by volume of the spherical area, we get the total force which acts on the unit mass and is centrifugally directed:

In the SI system:; radius of the universe; average density of substance in the Universe; we assume that the propagation speed of the information on the changes of the gravitation potential is equal to the light speed:. Thus, dimensionless number

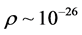
The fact that this number turned to be close to one is more likely coincidence, than exact validation of the theory. Speaking of the Universe radius, much less of the average density of the substance in it, today we can speak in terms of the orders.

So, the centrifugal force which acts from the side of the Universe on the body with mass m, that moves along the circle with radius a with angular velocity:

8. Conclusions

As already mentioned, the theory of relativity had given the answers to the questions that were set to physics by the experimental data. Mechanics of Galileo-Newton resulted in the insoluble contradictions: to explain it with the help of the presence of stellar aberration, experiment of Fizeau and Michelson-Morley experiment was impossible. To remove this contradiction allowed the postulate of independence of the light speed in vacuum from the motion of the source and the observer. In future, the experimental data, obtained in the laboratory, with high accuracy confirmed the correctness of SRT. Key and most convincing of these experiments was the experiment of Ives and Stilwell.

In the present article, the attempt was made to find the solution of the same problem, different from the solution of Einstein. The proposed solution proceeds, in particular, from the proposition on the existence of the initial reference system, wherein the light speed in vacuum is isotropic. The obtained results do not contradict the logic of the theory of relativity and, as shown in the article, the experimental difference of them from SRT results is so small that it cannot be fixed in the absolute majority of laboratory experiments. However, there is the difference, and its detection does not require the precision measurements or expensive experiments. Such experimental verification would allow answering the question, whether the proposed here logic is pure abstraction or it corresponds to the physical reality.

Acknowledgements

The author thanks S.A. Paston for valuable remarks and for carried out computation, realizing the transition to the Lorentz transformation form.

Cite this paper

Leonid Filippov, (2016) Heuristic Approach to Kinematics and Electrodynamics of Moving Bodies. World Journal of Mechanics,06,52-83. doi: 10.4236/wjm.2016.63006

References

Appendix 1

From the Abs viewpoint the picture is: both at rest and in motion the length of the segments AB and A'B' are equal to L. Segment AB moves with the speed, segment A'B'―with the speed. In the center of each segment is located the observer (F and E) (Figure A1).

E system “overtakes” F system, at that the contact of A and A' points and B and B' points from the viewpoint Abs occurs simultaneously. Abs observer sees: the signal from B and B' point’s contact came to F earlier, than the signal from A and A' contact by

This means that from the viewpoint of the F observer who synchronizes the clock with the light impulses and uses Einstein definition of the concept of simultaneity of the different-place located events, segment A'B' in the E system is longer, than the segment AB in the F system. Let us form up in the F reference system such segment ab with center in the F point so as from F viewpoint it would be equal to the segment A'B' in the E system: the light

signal flied out of the b point later than out of B point by the time and moved to the left relative to the F observer with the velocity. Signal out of a point flied earlier, than out of A, by the time and

moved to the right with the velocity. These signals came to the center of segment ab―to the F observer― simultaneously, wherefrom he concludes, in the framework of the accepted axiomatic, that his segment ab is equal to the length of A'B' segment in the moving reference system.

Let us find the length of ab segment, which is equal l₁. Signal out of b point flied later than out of a point by the time.

;

And, as the result:

; (1.1)

So, when “light” observation from the “lagging” system, takes place the length increase of the moving body along the line that is parallel to the motion speed, in comparison with its length at rest.

Similar reasoning is for the E observer. From Abs viewpoint: the light signal from the contact of B and B' came to E point earlier, than the signal from the contact of A and A' by

That is, from the E viewpoint, the segment AB in the F system is shorter, than segment A'B' in the E system. Let us form up in the E system the segment a'b' with center in E point, the length of which from E viewpoint, is

equal to the length of segment AB in the F system: signal flied out of B' later, than out of B' by the time and moved to the left relative to the E observer with the velocity. Signal out of a' flied earlier, than out of A', by and moved to the right with the velocity. These signals came to E point simultaneously.

Let us find the length of segment a'b', equal to. Signal out of b' point flied later, than out of a' by the time

;;

As a result:

; (1.2)

When observing from the “overtaking” system, takes place the decrease of the segment length in comparison with its length at rest.

Described picture from F observer viewpoint:

From F viewpoint, the lengths of segments ab and A'B' are equal―signals from their contact come to F point simultaneously. E observer flies to the right (towards signal out of B' and moving away from the signal out of A'), he sees the signal out of B' earlier, than out of A', therefore, in logic of “light simultaneity”, from E viewpoint the segment ab is shorter, than A'B'.

From the E observer viewpoint:

From the E viewpoint, the lengths of a'b' and AB segments are equal: the signals from their contact come to the E point simultaneously. The F observer flies towards signal out of A and moves away from the signal out of B, he sees the signal out of A earlier, than out of B, i.e. from the F viewpoint the segment a'b' is shorter, then AB.

Let us calculate, in how many times one of the segments is shorter than the other in each of two considered cases.

From E viewpoint the length of the ab segment (flying by with the velocity―see Figure A2) is longer, than the length of the a'b' segment, located in E itself, in so many times, in how many times the ab length is actually greater, than the AB length―at rest. The length a'b' at rest―is. “Genuinely”―i.e. from the Abs observer viewpoint, the length AB―is L. We get:

So, from the E observer viewpoint, the length of the moving segment ab is less, than the length of the resting segment A'B':;.

Similarly―“to the reverse side”: from the F viewpoint the length of a'b' (flying by with the velocity―see Figure A3) is less, than the length of the segment ab, located in F itself, in so many times, in how many times the length a'b' is actually less, than the length A'B'―at rest. We get:

It means, that from the F observer viewpoint, the length of the moving segment a'b' is less, than the length of the resting segment AB:;.

As we see, in this case the symmetry is observed.

Appendix 2

The simplest case: the laboratory reference system coincide with the initial one, velocities are parallel. As shown above, of from the initial reference system viewpoint the F system has the velocity, and from the F viewpoint

the E system has the velocity, then from initial reference system viewpoint the E system has the velocity,).

Expressing in terms of and, we get:.

Further, “to the reverse side”: if from the then from initial reference system viewpoint the E system has the velocity viewpoint the E system has the velocity, and from the E viewpoint the F system―velocity

, then from the then from initial reference system viewpoint the E system has the velocity system viewpoint the F system has the velocity,). We express in terms of:

so,

Let us show, that the resulting speed that is obtained when adding of two speeds, each of which is less than c, is always less than e. Having assumed that, where both and are positive and less than e, we have:

;, here;;

Assuming in this expression or, i.e. or, we obtain in the both cases:. As we see, the light speed, added with the speed which is less than the light speed, cannot be changed.

It is possible to obtain the same result by applying to the speed addition formula the value or. At we get for any value of.

Further, more general case: the laboratory reference system does not coincide with the initial one. Three reference systems, that are designated as “1”, “2” and “3”, move along one line from the initial system viewpoint, and their velocities measured by the observer in the initial system are equal to, and correspondingly. At that, the velocity of number 2 system, measured by the observer in the number 1 system, is equal to u, and the velocity of “number 3”, measured by “number 2”, is equal w.

From Formula (8):

and.

At the same time we can write the expression for the velocity of the “3” system, measured by the observer in the “1” system:. It is impossible to express this value only in terms of u and w, since this

would mean its independence from the motion of the considered reference systems relative to the initial system. Nevertheless, the general formula for, expressed in terms of the relative velocities, is more obvious and suitable for analysis. So:

In case when the “1” system coincide with the initial one, i.e., this expression transforms into already known formula.

Further, at, i.e. in case, when the “3” system―is the light, and this means, we get:.

Formula for, at the addition of velocities, each of which is less than the light speed in those reference system, wherein it is measured, gives the result, which is always less than the light speed. We assume the velocity, where. This means, that the “3” system moves with the speed which is less than the light speed, and from the initial reference system viewpoint its speed, where―some positive number. Applying theses values to formula for and also assuming and (that automatically results in), we obtain, as the result, the expression for velocity that is less than the value.

Appendix 3

Having set, we get:

The value is less than the value by six orders; the product of the second additive from the first bracket by the second additive from the second bracket is less than the value by the same six orders. Neglecting them, we get:

;

Appendix 4

Atomic radiation, the law of conservation of energy:

(4.1)

The law of conservation of impulse:. At that;, therefore:

where from:

(4.2)

Subtracting (4.2) from (4.1), we get:

(Physical meaning of this equation: difference at the radiation remains constant.) Having expressed from this and applied to (4.1), we obtain:

(4.3)

Let us carry out the same reasoning with regard to the reference system wherein the considered atom prior to the emission of the light quantum was at rest. This system moves relative to the initial one with the velocity, and

the light speed, measured in it, is equal. The velocity of atom prior to emission in this reference

system is equal to zero, let us designate the velocity after the emission (its direction is opposite to the direction of the emitted light quantum).

As before we assume the law of conservation of energy and the law of conservation of impulse to be true at the light emission, whatever reference system the observer would be located. Therefore, all the performed above reasoning may be carried out for the observer, situated in the reference system, connected with atom prior to emission. Let us designate the frequency of the emitted light quantum, measured in this reference system.

Having performed given above computations for the system which moves with the velocity (at that, the direction of velocity should be taken into account in the law of conservation of impulse), we obtain the analogue of the expression (4.3):

.

Satisfaction of the energy conservation law means also the following: atom, resting in the initial reference system, and the identical to it atom, resting in the reference system that moves relative to the initial one with the velocity, at the transition out of state with energy to the state, emit the light quanta, which frequencies, each measured in its system, will be equal. Designating “recoil velocity” in the initial reference system as and

performing the same computations, we obtain for the initial one:.

Let us find the relation between “recoil velocities” in two reference systems:. Considering, that, it can be assumed with the vast accuracy that, and therefore,.

Further, we use the formula of velocity addition (8). Applying to it the velocity value (taking into account the direction of this velocity) we get:. We expressed from it and apply to (4.3):

For determination of the light frequency, measured at the real experiment, the obtained formula may be simplified. Let us consider those fact, that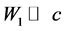. This means, that velocities and at the measurement are practically indistinguishable. Therefore, simplifying, we replace in the formula these both values by “V”. Further,

for the same reason the difference of the multiplicand from unity negligible little effects the result. Besides, having discarded the fourth-order additive, we assume. As a result, we

obtain the expression for the light frequency, measured by the observer in the initial reference system, under condition, that the light source moves relative to it with the velocity V:

We considered the case of the light quantum emission in the direction of the atom motion. For the case when the light is emitted in the direction that is opposite to the source velocity, above performed computations give:

Appendix 5

Let it now be. In this case, as we see, the Formula (1) should be used, in accordance with which, when observing from the “lagging” reference system, there takes place the increase of the moving body length along the line, that is parallel to the motion velocity, in comparison with its length at rest. That is, in this case takes place the

decrease of the intensity in comparison with rest. Factor of this decrease is.. Further, as we see, follow exactly the same computations, as in case of.

Further, we consider the case, when the charge-carrier velocities in the conductor and the test particle are opposite. For this, we will derive the length transformation formula in the case, when the reference systems, wherein the observer and the measured segment are located, move relative to the initial reference system in the opposite directions (Figure A4).

Let us carry out the same reasoning, as when deriving of the Formula (6). From the initial reference system viewpoint, the flight time of G point over the whole length of C'D' in the H system is equal. The clock is situated in G, the events are same-place-located there, this means that G itself will obtain the same value.

From the H system viewpoint (according to the clock of C' and D'), the time of G point passing over the whole segment C'D' is longer, than by the value, by which, from the initial reference system viewpoint, are fast the D' clock relative to C' clock, i.e. by. This means,

Therefore,

;

(The events are same-place-located in the G reference system.)

Further, considering already known relations between the transformation of length and time term, we obtain: when measuring from the H system of the segment length, which is equal at rest L, located in the G system, is

equal (decrease of the length in comparison with the rest.)

We get: from the viewpoint of the test particle which moves with the velocity u relative to the initial reference system, the intensity created by the charge-carriers that move relative to the initial reference system in the opposite

direction with the velocity V increases in comparison to rest by times. This means,

Further, as in another considered cases,. As we see, the repulsive force in this case is bigger:―opposite directed currents repulse. And again the expression for the Lorentz force:

Appendix 6

The E observer is located in the system which rotates with the constant angular velocity w relative to the motionless Universe that acts the role of the initial reference system. Circle radius, along which moves the E observer, is equal а.

In Figure A6 to the left:, ,; to the right:,..

In rest, from the initial system viewpoint, D and A points, which are motionless located upon the circle with radius R, were seen in the E point at the small angle d. In order to obtain the DA arc “in the shot”, made at the Е point, the light signal out of the D point should fly out later, then out of the A point, by the time:

Upper hemisphere

Hence, and, disposing the addition of the order of (since), we get:; similarly:

(6.1)

When the E observer moves in the described clockwise way, the E point more rapidly approaches to the A point, compared to the D point. That is, in the point (1) the signal from the A point comes earlier, then from the D point-it is the question of the same signals, mismatched by, which simultaneously come flying to the resting E―Figure A6 to the right.

Similarly, for Figure A6 to the left: E more rapidly move away from the D point, then from the A point. That is, in these both cases the E observer obtains “in the shot” the decrease of the length in comparison with the length, measured at rest: the same arc will be seen in the shot at the angle, which is less, than angle d.

Figure A6: in point (1) the segments and become the segments and correspondingly―the E observer moved off clockwise along the circle of the radius a by the distance x.

In the point (1) the difference between y₁ and y₂ becomes less, than, the signal from the A point come flying in the point (1) earlier, than from the D point by the time of

since, then (6.2)

From the initial system viewpoint the E observer moves with the velocity V.;

; hence

Considering (6.1) and the fact, that, , we get:

;

Applying all this to (6.2), we get:

And considering, that, , ,

The first additive will be of the same order as the second only at so small, that, i.e. it may be discarded as acting no role:

(6.3)

This is measured in the initial system, at that the events are same-place-located in the E system, i.e. the E observer will obtain the same, therefore,

(6.4)

Here―the angular velocity of A and D points, measured in the E system;―the angular value of DA arc;―the value of arc, that replaces in motion the DA arc “in shot” (in the upper hemisphere); w_*1―the an-

gular velocity of D and A points, measured in the E system., where―the angular velocity, measured in the initial reference system. Further, , however, we will assume, since;, i.e., considering that, within limits of the accepted accuracy.

Combining all this, we set (6.3) and (6.4) to be equal and, discarding the knowingly small additives, we obtain:

; (6.5)

So, for the “upper” hemisphere () at measurement from the moving system, decrease of length of the segment, located in the initial reference system, is observed, compared to its length at rest.

Completely analogous reasoning for the “lower” hemisphere (, Formulas (6.3) and (6.4)) gives the following result:―length increase. At that Formula (6.5) remains to be true; ().

Further, the same reasoning―for the space, in the spherical coordinates. In this case, to Figures A5-A8 corresponds the Figure A9:

Further,

As the result, completely analogous to the Formula (3), we get:

and accordingly,

This means, that the tangential element of the length at the distance R from the center of rotation is reduced in comparison with rest in k times, where

,

that, taking into account the sign of, gives the following:

1) at there will be the reduction of the length in comparison with the rest―,

2) at -the increase of the length―.

So, at the uniform distribution, for example, of the charge over the spherical volume, the centrifugally directed force acts on the material point which moves along the circle with radius a with the angular velocity―as the result of the interaction of this material point with all the volume, contained inside the sphere and asymmetry, caused by the signal lag in the reference system that is different to the initial.

Appendix 7

Let us apply the obtained result to the sphere with radius with the uniform distribution by the charge volume (or the gravitating mass) (Figure A10).

“Vertical” projection of the intensity, originated by the point of the “upper” hemisphere with the spherical coordinates, , R in the A point, which moves in the above described way:

Here―the intensity, originated by the same material point in the case, when the A point is motionless (Figure A11).

Analogous computations for the point of the “lower” hemisphere with the coordinates, , R give:

“Vertical” projection of the total intensity, originated by such two symmetrical points:

In the framework of the accepted accuracy:

;

We replace the material point by the element of volume with the same coordinates:

For both electrostatic and gravitation interaction, the inverse square law if fulfilled. Let -the gravitation force which acts on the material point of the unit mass, located in the A point and moving in the considered above way.

Then, , where―the mass of the unit volume; gravitating mass is uniformly distributed over the spherical area from to.

, where―the solid angle;

Integrating the obtained expression over the volume of the spherical area, we get the total force which acts on the unit mass and is centrifugally directed:

; ()