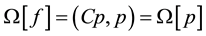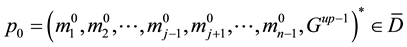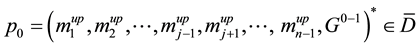Received 15 October 2015; accepted 12 December 2015; published 15 December 2015

ABSTRACT

We consider the problem of determining the center of mass of an unknown gravitational body, using the disturbances in the motion of observed celestial bodies. In this paper an universal approach to obtain the approximate and stable estimate of problem solution is suggested. This approach can be used in other fields of Science. For example, it can be applied for investigation of interactions between fields of forces and elementary particles using known trajectories of elementary particles motions.

Keywords:

Astrodynamics, Le Verrier Problem, Regularization, Main Hypothesis

1. Introduction

In 1843-1845 famous astronomers and mathematicians Urbain Jean Le Verrier (1811-1877) and John Couch Adams (1819-1892) independently of one another performed the mathematical research and came to the conclusion that the Solar system includes a celestial body (at least one) which has not observed earlier.

In fact not only the existence of a previously unknown planet has been proven, but also its orbit has been determined with an accuracy, which was sufficient for its detection and surveillance. The planet Neptune has been discovered as result. Mathematically these problems belong to the category of inverse problems of mathematical physics, i.e., to ill-posed problems. The solution of this problem was executed by the method of least squares using some hypothesizes. After discovering Neptune, Le Verrier started the recalculation of theory motion of Uranus by taking into account the motion of Neptune. After finishing his investigation, Le Verrier was able to achieve results with high accuracy, which unfortunately still disagreed with results obtained by observation. This difference was not due to an error in theory or observation [1] -[3] . Theoretical success of Adams and Le Verrier was attracted thousands of enthusiasts and professional astronomers and mathematicians. Hundreds of scientific calculations were published based on the work of Le Verrier and Adams, but the results yielded nothing. There were studies, which simultaneously proved the existence of up to two dozen new celestial bodies [3] .

Much later it was discovered a natural property of inverse problems their instability.

Of course, our knowledge of the Solar system has not been and will never be final and the level of our knowledge is entirely determined by the level of theoretical and observational studies. However, a theoretical analysis of the constructed motion of large (and primarily external) planets indicates, that there are yet unexplained discrepancies between theory and observation. Despite the fact that the theoretical parameters of motion were refined with results made from observation, which were made over a long period of time. For example, there are latitudinal variations in the motion of Uranus and Neptune and the deviation in the movement perihelion of Halley’s comet, that cannot be explained by gravitational forces of known solar system bodies. These circumstances have led to the fact that in the 60s of the last century a hypothesis for the existence of a tenth planet emerged. This 10th planet should have a mass equal to the mass of Jupiter, with an approximate distance to the sun of 60 AU and an orbital tilt of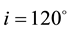. The joint solution of the equations of motion of known planets and of a hypothetical planet and subsequent thorough review of photographic plates of “suspicious” parts of the sky, have not yielded any positive results. Although, according to preliminary estimates, the hypothetical planet was supposed to be 13 - 14th magnitude, and on photographic plates were considered objects to 16.5 magnitude, but the tenth planet was not found.

Analysis of solution methods of Le Verrier and Adams shown these methods did not take into account the inaccuracy of mathematical model of planets motion. The success of their investigations was guaranteed with help of right hypothesis about tilt of unknown planet orbit to plane of the ecliptic and orbit eccentricity.

This fact is explained failure of big numbers of investigations after Le Verrier for searches of planet Pluto.

Thus the development of stable methods of approximate solutions of the inverse problem astrodynamics in more general statement remains relevant.

2. Statement of the Inverse Problem Astrodynamics

We consider n interacting masses moving under the forces of mutual attraction in an inertial coordinate system. Masses 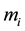are given the index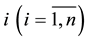, 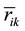denotes the vector connecting the mass 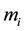and the mass. According to Newton's law the resulting force 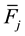acting to the mass 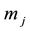is equal [4]

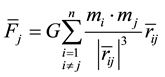, (1)

where G is the gravitational constant.

The mass 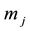under the influence of this force executes the motion which satisfies the differential equation

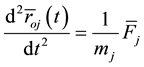, (2)

where is the radius vector connecting the origin of inertial coordinate system with the mass.

Let us make the transition of the variables to the variables 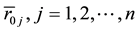in Equation (2)

. (3)

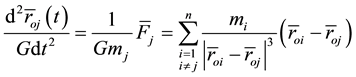
It is assumed that among n gravitational masses the location of only mass 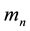is unknown. The last term in the sum on the right of Equation (3) is uncertain.

Equation (3) takes the form

, (4)

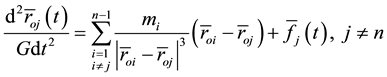
where 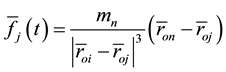is the function to be determined.

In terms of projections on the axis of the inertial coordinate system the Equation (4) can be written in the form:

, (5)

, (6)

, (7)

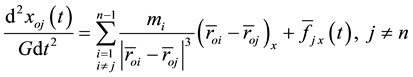
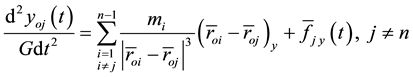
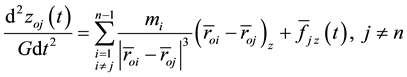
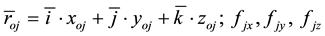
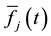
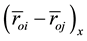
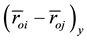
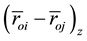
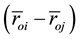
where are the projections of the vector of on the corresponding axes of the inertial system coordinates, , , are the similar projections of the vector.

Let us integrate Equations (5)-(7) twice from to t:

(8)

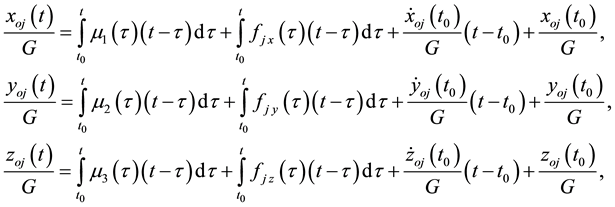
where, ,.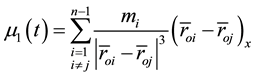

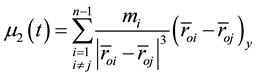
Each equation of the system Equation (8) can be presented in the form

, (9)

where

,

,

.

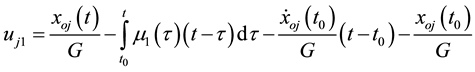
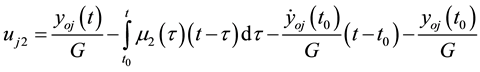
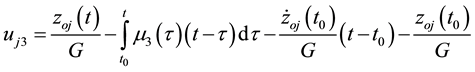
Equations (9) are known as Volterra integral equations of the first kind with respect to the unknown functions [5] .

By finding the solutions of the Equations (9) 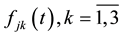you can restore the force vector, exerted by the mass on the mass up to a constant factor.

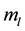
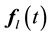
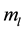
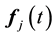
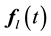
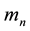
Performing similar calculations and solving equations of the type Equation (9) for the mass, we can determine (up to a constant factor) the force, which is acting on the mass from the mass. The intersection of the lines of action of the vectors and gives the position of the mass in space (in a chosen inertial system).

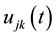
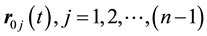
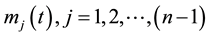
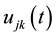
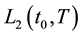
As is easily seen, are defined by the functions, which are assumed to be known from astronomical observations of the motions of the masses, which do contain some errors. It is assumed that functions belong to functional space.

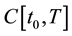
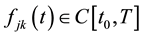
Solution of the Equation (9) in the physical sense must also belong to, i.e.,. Under these conditions Equations (9) are an ill-posed problem [5] .

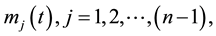
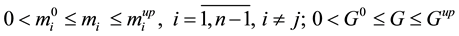
In the Equations (5)-(7) of motion the coefficients G are determined from astronomical observations and experimental investigations and so these values are known only approximately. Thus it is assumed that each coefficient in Equations (5)-(7) is in some interval:

. (10)

Introduce into consideration the following notations

,

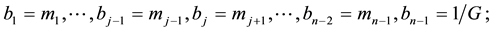
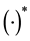
where is the sign of transposition.

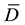
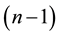
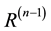
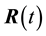
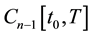
The Inequalities (10) define a closed region of in the -dimensional Euclidean space. The set of vector functions forms a linear function space, which can be equipped with following norm [6] :

,

where.

The Equation (9) can be written in the form

, (11)

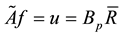
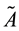
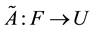
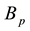
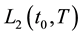
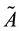
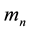
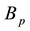
where the operator is a compact operator, , is a linear restricted operator, which transforms elements of the space into the space. Let us assumed that the functional space as according of the physical sense the searching functions must be the continuous functions.

The operator in Equation (11) doesn’t depend on parameters of the mathematical model of the motion of body. It is easy to see that the operator in Equation (11) is a completely continuous operator [6] . The operator depends on the specific values of the parameters of the mathematical model of the process, which is p.

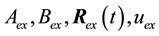
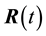
We denote by, respectively, the exact operators in Equation (11), the exact vector-valued function and the exact function of u in the right-hand side of Equation (11).

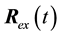
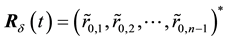
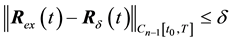
Suppose instead of Equation (11) is given by the approximate function for which the following inequality is valid

.

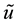
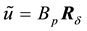
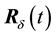
The approximate value of is the right side of the Equation (11). So will match the data.

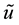
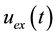
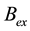
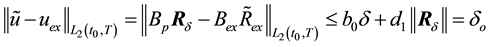
Let us estimate the deviation of of , assuming that the exact operator is linear:

, (12)

where,.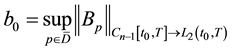

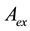
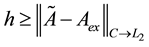
Since real processes can be described by mathematical methods only approximately. It is assumed that the exact operator in the Equation (11) differs from the approximation of the operator (if the exact operator is linear) by a predetermined amount

.

In this case it is possible to use the algorithm for solving the inverse problem with approximate operator 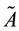proposed in [7] .

However, the assumption of linearity of the exact operator 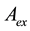and of information relatively of size of h in most cases does not correspond to reality.

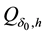
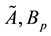
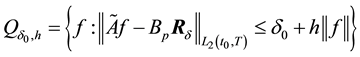
Then the set of possible solutions of Equation (11) with account of the linearity of operators will have the form:

. (13)

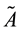
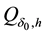
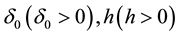
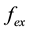
It is easy to show that if the operator is a compact operator, then the set is an unbounded, closed and convex set for any. Then it is assumed that exact solution of Equation (11) belongs to functional space.

For solving ill-posed problem Equation (11) we use the Tikhonov regularization method with the stabilizing functional

, (14)

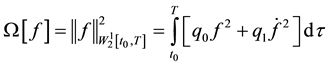
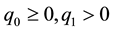
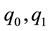
where, are constants.

Thus, the problem of finding an approximate solution of Equation (11) reduces to the solution of the extreme problem:

. (15)

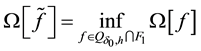
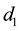
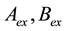
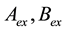
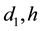
It should be noted that there is no way to determine the size of, since the exact operator is the unknown operator. Moreover, the exact operators cannot be constructed, in principle, because the mathematical models, which describe the real processes, are always approximations. Of course, under certain assumptions about the exact operators we can get some error estimates of, but such estimates are unrealistic.

Therefore, the approximate solution of inverse problems of measurement are not of interest for practical use due to instability of the solution.

The way out of this impasse exists, if by the investigation of inverse problems of measurement restrict only some estimates of exact solutions.

3. The main Hypothesis and Results

The set of possible solutions of Equation (11) for fixed operators has the form:

(16)

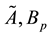
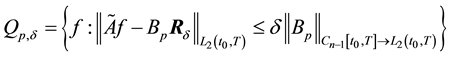
Let us considered the following extreme problem

, (17)

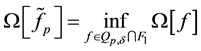
The regularization parameter 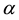can be find from condition:

. (18)

To obtain useful information on the exact solution of the inverse problem the use of the following hypothesis (main hypothesis) is suggested: the inequality is valid

, (19)

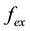
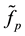
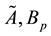
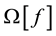
where the function is an exact solution of the inverse problem of measurement Equation (11) with exact initial data, the function is the regularized solution of the inverse problem Equation (11) with the fixed operators (which are given the adequate description of the physical process) and stabilizing functional.

If the exact operators are linear, then the Inequality (19) is obvious.

Evaluation of the exact solution, obtained by the method of regularization on the set, for fixed operators is some function on vector, i.e.,. The function can be significantly different from the exact solution.

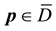
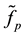
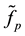
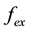
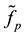
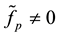
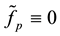
The estimate allows us to conclude the existence of an unknown planet with a guarantee (in case), or its absence but without guarantee (in case).

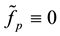
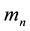
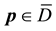
If, it is also possible to have a real celestial body as this does not take into account all the operators. To study the effect of the parameters of mathematical model, we need to examine all possible estimates.

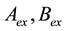
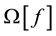
Note that the preparation of estimates does not use properties of the exact operators. To assess the existence of an exact solution, it is possible to use the stabilizing functional.

We give sufficient conditions for the existence of an element.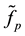

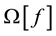
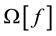
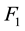
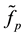
Theorem1. Let be a stabilizing functional for, the func-

tional be continuous, non-negative and strictly convex on. Then the solution of the extreme problem (15) exists, is unique for any and any.

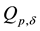
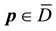
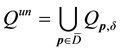
In order to study the influence of the process parameters on the estimation of the exact solution, we consider the union of the sets for all vectors:

. (20)

The set 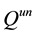is unbounded as a union of unbounded sets.

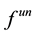
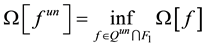
Let be a solution to the extreme problem:

. (21)

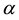
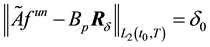
The regularization parameter was determined by the method of discrepancy:

. (22)

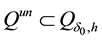
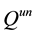
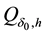
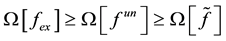
Since, using instead of in Equation (15) will yield more accurate estimates for the exact solution. This approach is based on the work of [8] . In addition, it is obvious that the inequality

(23)

is valid.

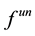
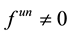
Evaluation of the exact solution of allows us to conclude on the existence of an unknown planet with a guarantee in case or its absence, but without guarantee in case.

To study the influence of the parameters p on the estimation of the exact solution of the inverse problem it is necessary to have a possibility to select an operator from operators which satisfies the following condition:

(24)

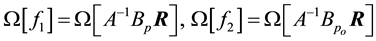
implies the inequality

(25)

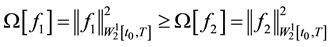
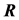
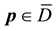
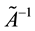
for any possible and any; is the inverse operator to.

Subsequently, the operator in the right-hand side of Equation (11) will be called as “special minimal operator” in the sense of the Inequality (25).

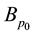
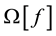
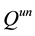
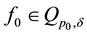
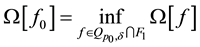
If the operator exists and is unique, then the problem of finding the greatest lower bound of the functional on the set will have a solution, which coincides with the solution of the more simpler extreme problem [9] : find an element for which the equality

(26)

holds.

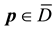
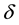
The problem (26) has a solution for every and, since the conditions of the Theorem 1 are satisfied.

In this case the following inequality holds for any: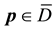

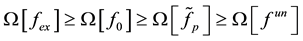
. (27)

Evaluation of the exact solution allows us to conclude the existence of an unknown planet with a guarantee in case or its absence, but without guarantee in case.

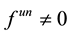
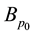
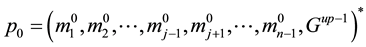
Theorem 2. Special minimal operator in the Equation (11) exists, is unique and corresponds to the vector

.

Proof. Let be a realization of an astronomical observations. Consider the problem of determining the exact lower bound of the functional in for a fixed. By the Weierstrass theorem the continuous functional is attained at some vector.

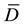
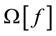
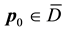
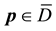
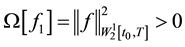
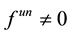
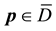
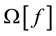
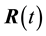
For any the function is strictly positive since

when, for all.

The function for a fixed can be represented as a quadratic form

where C is a real symmetric matrix.

Coefficients of the matrix C are given by:

.

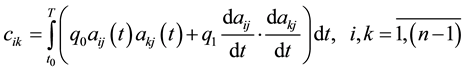
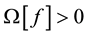
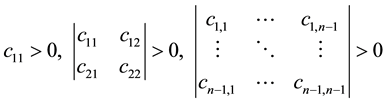
Since for, then the Silvester’s inequalities gives us:

.

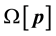
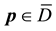
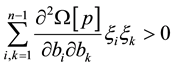
A necessary and sufficient conditions for strong convexity of to are the following [10] :

(28)

for any and any.

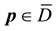
Quadratic form (28) is positive as

.

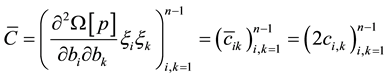
Therefore, is strongly convex on.

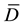
Similarly, [10] we prove that 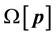achieves the greatest lower bound in a single point in the domain

for any. □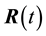

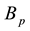
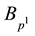
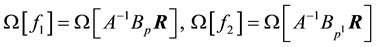
Suppose that among the operators there is an operator such that if the condition

, (29)

then the inequality

(30)

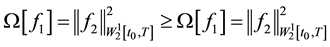
for any possible and any; is the inverse operator to.

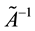
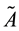
Subsequently, the operator 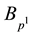in the right-hand side of Equation (11) will be called “special maximum

operator” in the sense of satisfying Inequality (30).

If the operator 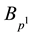exists and is uniquely determined then we can consider the solution of the following

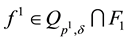
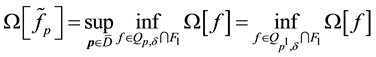
extreme problem: find an element for which the equality

(31)

holds.

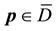
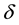
The problem (31) has a solution for any and, since the conditions of Theorem 1 are satisfied.

Thus obviously the following inequality is valid:

. (32)

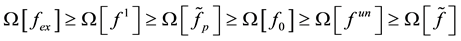
Theorem 3. Special maximal operator 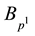in the Equation (11) exists, is unique and corresponds to the vector

for any.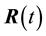

Proof. The proof is similar to Theorem 2. □

4. Conclusion

In this paper we proposed an algorithm for finding the coordinates of an unknown gravitational mass as a result of astronomical observations. This problem was solved first by Urbain Jean Le Verrier and John Couch Adams. Here a more universal approach was suggested. The proposed hypothesis allows us to exclude the error of the approximate operator from the calculations. Also conditions for the existence of an approximate solution were obtained and several non-standard formulations of inverse problems were considered. Suggested approach can be used in other fields of Science. For example, it can be applied for investigation of interactions between fields of forces and elementary particles by help of known trajectories of elementary particles motions.

Cite this paper

YuriMenshikov, (2015) Inverse Problem of Astrodynamics. World Journal of Mechanics,05,249-256. doi: 10.4236/wjm.2015.512023

References