Received 20 August 2015; accepted 27 October 2015; published 30 October 2015

ABSTRACT

Two dimensional numerical simulations of flow around a rotationally oscillating circular cylinder were performed at Re = 1000. A wide range of forcing frequencies, f_r, and three values of oscillation amplitudes, A, are considered. Different vortex shedding modes are observed for a fixed A at several values of f_r, as well as for a fixed f_r at different values of A. The 2C mode of vortex shedding was obtained in the present study. It is important to point out that this mode has not been observed by other investigators for rotationally oscillating case. Also, it is verified that this mechanism has great influence on the drag coefficient for high frequency values. Furthermore, the lift and pressure coefficients and the power spectra density are also analyzed.

Keywords:

Rotationally Oscillating Cylinder, Vortex Shedding Modes, Drag Coefficient

1. Introduction

It is widely known that the vibrations induced by vortex shedding process may have negative effects in engineering systems, such as economic loss, damage of installations, and very frequently with environment-related consequences. Thus, although the fluid flow around circular cylinder is a classical problem in fluid dynamic due to its simple geometry, this is a reason for which in the last decades, a great deal of effort has been devoted to the development of numerical and computational procedures for dealing with the problem of vortex shedding phenomena. Comprehensive studies on this subject have been reported in books [1] -[3] .

In applications in which a circular cylinder under rotational oscillations is involved, the flow dynamic is different from those observed for stationary cylinders and has fascinated researchers for a long time [4] - [7] . In this case, two important parameters related to the prescribed motion are the forcing frequency and amplitude. Hence, the characterization of those parameters on the flow structure becomes of capital importance.

Among some studies over rotationally oscillating cylinders, the so-named Hybrid Vortex Method and the Discrete Vortex Method have been proposed [8] [9] to investigate the process of vortex formation for a set of forcing frequency at Reynolds number 200 and 1000. Srinivas and Fujisawa [10] have used the unsteady form of Reynolds-averaged Navier-Stokes equations combined with the k-e model of turbulence in order to determine the effects of several parameters on the flow structure over a rotationally oscillating circular cylinder for Reynolds in the range 2000 - 3.0 × 10⁴. Ray and Christofides [11] studied a control system based on the open-loop simulations to reduce the effects of drag exerted on a circular cylinder subjected to rotational oscillations for Reynolds number in the range 100 - 500.

The present study focuses on two-dimensional, incompressible viscous flow over a rotationally oscillating circular cylinder by using the Immersed Boundary Methodology (IBM) [12] in order to investigate the oscillation effect in the wake structure behind the cylinder, at different forcing frequencies and amplitudes. In addition, the influence of those parameters on the drag, lift and pressure coefficients and the power spectra density are also analyzed. The simulations were carried out for flows at Re = 1000, amplitudes equals to 1, 2 and 3 and for various frequency ratios. The used methodology has showed a promising tool to simulate mobile bodies and in the present study, it captures the vortex shedding mode, named 2C, which has not been found for the case of rotational oscillation by other researchers.

2. General Aspects of the Numerical Methodology

Mathematical Formulation for the Fluid and for the Fluid-Solid Interface

One approach, which is not very common to solve the Navier-Stokes equations, is the so called velocity-vorticity formulation [13] . Flows can also be modeled by these equations in primitive variables [14] . In this section, the IBM combined with the Virtual Physical Model (VPM) [15] is summarized. For a viscous and incompressible flow, the IBM is based on the Navier-Stokes Equation (1) with an added force source term which acts on the fluid so that a particle perceives the existence of the solid interface. The continuity Equation (2) is also expressed.

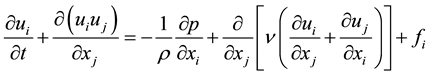(1)

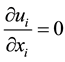(2)

where 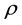[kg/m³] and v [m²/s] are the specific mass and the kinematic viscosity, respectively; 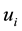[m/s] and p [N/m²] are, respectively, the i-th velocity component and the pressure; 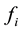[N/m³] is the i-th component of the Eulerian force calculated as follows:

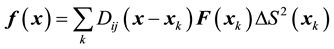. (3)

In Equation (3) 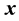[m] and 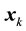[m] are the position vectors of a Eulerian and a Lagrangian point, respectively, and 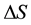[m] is the arc length centered in each Lagrangian point, which is evenly spaced as shown in Figure 1(a). 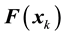[N] is the Lagrangian force over the interface, and 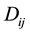[m⁻²] is the distribution function [16] .

At this point, the mixed Eulerian-Lagrangian formulation is retained, in which the Eulerian fixed grid describes the flow and the Lagrangian grid (which can be fixed or not) describes the immersed body. These meshes are geometrically independent from each other, and this fact enables to study the flows around simple, complex, movable and deformable geometries, without any remeshing process. These two formulations are coupled by a force field obtained at the Lagrangian points and then distributed over the Eulerian nodes in the body neighborhood. By this strategy, one can use a simple Cartesian grid and it is not necessary to move the grids. According to the VPM [15] the Lagrangian force field is calculated based on the momentum balance over a fluid

particle placed on the Lagrangian points.

By considering a particle of fluid placed on the fluid-solid interface as illustrated in Figure 1(b), the Lagrangian force field is given as follows:

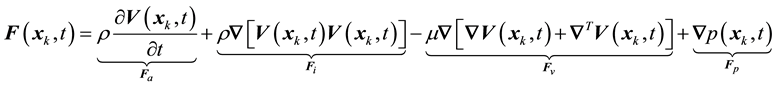(4)

where 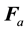[N] is the acceleration force, 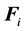[N] is the inertial force, 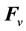[N] is the viscous force, and [N] is the pressure force. After obtaining the force field given by Equation (4), its values are distributed over the Eulerian nodes by using Equation (3) to generate the Eulerian force field that models the immersed body.

3. Numerical Method

A number of mesh-free methods have been developed in recent years [17] to circumvent the polygonisation problem found in the classical numerical methods. Here, the momentum and continuity equations are numerically solved using the finite difference method through the fractional step scheme based on the pressure correction concept [18] . Given the initial velocity, the pressure and the force fields, an estimated velocity field is obtained. This velocity field is used to calculate the pressure correction, by solving a linear system of algebraic equations, for which the Modified Strongly Implicit Procedure (MSI) [19] is used. The Poisson equation gives the coupling between Equation (1) and Equation (2). Also, it provides values of pressure that allow that the velocities components, obtained by using the Navier-Stokes equations, satisfy the mass conservation condition. The time discretization is done by the second order Runge-Kutta method [20] . The estimation of the velocity is calculated as:

(5)

where [m/s] is the estimated velocity component, [s] is the computational time step and is the substep index. The Poisson equation for pressure correction, , with the source term given by the divergent of the estimated velocity, is expressed by:

(6)

and the velocity field is updated by solving the algebraic equation. The previous pressure field and the correction pressure are used to calculate the updated values of the pressure field, according to the expression.

4. Results and Discussions

In this section, numerical simulations are performed to investigate the effects of the oscillating amplitude and forcing frequency on the flow structure of a circular cylinder. Figure 2(a) shows the computational domain which dimensions are 40d (Lu = 16.5d; Ld = 23.5d), in the streamwise and 15d (H) in the cross-stream direction, where d [m] is the cylinder diameter. The upper and lower boundaries are placed at 7.5d. The flow direction is from the

left to the right side of the domain and at the inlet, a uniform velocity profile is imposed. A Neumann boundary condition is used at the outlet and lateral boundaries, (,), respectively. For the pressure, the Neumann condition is used at the inlet and the Dirichlet condition is used on the outlet and in the lateral boundaries. On the surface of the cylinder, no-slip boundary condition is virtually employed using the IBM method. The time spent for each numerical simulation was about one hour. Also, the numerical code used herein was developed in Visual C.

Rotational oscillations at a prescribed set of frequency ratios and amplitudes are then imposed on the cylinder, where the tangential velocity over each Lagrangian point k, as shown in Figure 2(b), is defined as, where A [m] is the oscillating amplitude, [Hz] is the forcing frequency, and t [s] is the physical time.

The simulations are performed at Reynolds number 1000, with a time step chosen arbitrarily of for the first iteration. After that, and during the first 100 iterations, the time step size is increased gradually until, for which the geometry of the immersed cylinder is completely defined according to the immersed boundary methodology. The grid is composed by 400 × 125 points in x and y directions, respectively; the oscillating amplitude, a, ranges from 1 to 3, while the frequency ratio, , (is the stationary cylinder frequency) varies from 0 to 6. Many cases have been performed, however, for the purposes of this work, only selected cases are presented.

4.1. Vortex Shedding Modes

Figure 3 shows the vorticity contours for for different frequency ratios. When (Figure 3(a)), it is seen that the vortex street is aligned and symmetric with respect to the central axis of the flow, showing two single vortices shedding per cycle. It is so called 2S mode of vortex shedding. In the frequency range (Figure 3(b)) to (Figure 3(d)) the patterns of vortex shedding seem to be similar, but the sizes appear uneven. When (Figure 3(e)), one observes that the process of vortex formation is completely different from those of previous cases, and at the distance 12.5d downstream of the cylinder, the 2S mode appears again. Nevertheless, the transversal spacing is greater than that of the stationary case shown in Figure 3(a). When (Figure 3(f)), the 2S mode reappear. Figure 3(g) shows the P + S mode in which one pair and a single vortex are shed in each cycle. As frequency ratio further increases, Figure 3(h) shows that the wake structure remains essentially unchanged and similar to the stationary case. The no synchronized flow with the cylinder movement resembles to stationary cylinder flow, with some additional instabilities, due to the cylinder movement [21] . In other words, the instability caused by cylinder oscillation is limited to a region near to the cylinder, while far from immersed body, the vortices redirect to form the stable Von Kármán Street. This implies that occurs vortex-vortex interaction of the same sign, near to the cylinder, resulting in large scale vortices, whose values frequencies are close to the stationary cylinder frequency ().

Figure 4 shows visualizations of the flow structure obtained for A = 2 in the same frequency range as shown at Figure 3. In the range, one can note the presence of two vortex pairs shed per cycle, named as 2P mode. When, the wake vortices are similar to the classical Von Kármán Street shown in Figure 3(a), named 2S mode. However, the longitudinal and transversal spaces are larger than those corresponding to the stationary condition. In the frequency range, the evolution of the patterns remains unchanged, as shown from Figure 4(d) to Figure 4(f). In addition, it is observed that the transversal spacing is greater near

the cylinder and decreases away from it. When (Figure 4(g)) it can be noted the presence of two vortex pairs in each side of the central line of the flow, resulting in a conical wake structure. When is higher, it is observed that the vortex pattern is the same as the Kármán vortex street, indicating that for higher frequency values, the effect of rotational oscillation is confined to the flow near the cylinder, and its influence in the far field of the vortex structure is insignificant, as shown in Figure 4(h).

The patterns of vortex shedding from the cylinder in the near and far wakes are shown in Figure 5, for A = 3 and various values of. In Figure 5(a) one can note that the vortex street is not aligned with respect to the central axis of the flow and there are few vortex pairs in the wake. In addition, Figure 5(b) shows that the vortex

formation process is completely different from that of the previous cases, in which a new mode of vortex shedding, named as 2 C mode, appears. This mode indicates that two vortex pairs of the same signal are shed per cycle. It is important to mention that this mode was not observed by the authors cited in the references for the case of circular cylinders subjected to rotational oscillations. However, it is noted in the case of a pivoted cylinder as reported in Williamson and Jauvtis [22] .

In the frequency range, one can note that the vortex wakes are found to be basically the same as those obtained for A = 2 in the same frequency range. The result shown in Figure 5(g) demonstrates a new pattern of vortex shedding for which the double wake near the cylinder, composed by vortex of the same signal in each row coalesce at the final double street to form a single wake. As frequency ratio further increases, the pattern of vortex shedding tends to be the same from the non-oscillating case.

4.2. Time Histories of the Fluid Dynamics Coefficients and Power Spectra Density

It is known that the vortex shedding process causes fluctuations in the dynamic coefficients and affects the behavior of the flow structure. Figure 6 presents the time histories of the lift () and drag () coefficients as well as the power spectra of the lift coefficients for A = 1. Figure 6(a) shows that the transient behavior takes approximately 40 dimensionless time units (nine cycles in the present case) before reaching the periodic regime. From Figure 6(b) to Figure 6(h) one can note that the steady regime is reached more quickly than in the previous case due to fact that the cylinder’s oscillations accelerate the vortex shedding process. As can be seen in Figure 6(b), there is no harmonic behavior as observed for the previous stationary case, and the lift curve clearly resembles the shape of a signal with frequency that is beaten by another signal at, indicating that there is a significant interaction between these two frequencies. Also, from Figure 6(b) to Figure 6(d) it is verified that the amplitudes of the lift coefficient are greater than that for the stationary case. Moreover, it is observed a transition between the two vortex shedding modes when the frequency ratio is increased from (Figure 6(f)) (2S mode) to (Figure 6(g)) (P + S mode), but the oscillation amplitudes for the P + S mode are larger than that those corresponding to the 2S mode. This means that the change on the vortex modes has a strong influence on the time histories of the dynamics coefficients. As frequency further increases, the oscillation amplitudes tend to be the same of the stationary case, as can be noted by the comparison between Figure 6(h) and Figure 6(a).

When, Figure 6(a) shows that the lift spectrum for the stationary case is composed by one peak at the dimensionless frequency. When there are two prominent frequencies in the lift spectrum

shown in Figure 6(b). They correspond to the vortex shedding frequency, which is closed to and the forcing frequency. As the frequency ratio further increases from to (Figure 6(c)) shows two frequencies in the power spectrum, but there is a discernible drift of the vortex shedding frequency, , towards the forcing frequency,. The energy level of (secondary peak) is reduced and the frequency value is 83% of.

When, the frequency of vortex shedding, , locks-in to the forcing frequency, , resulting in only one dominating component in the lift frequency spectrum, as shown from Figure 6(d) to Figure 6(f). During the lock-in regime the wake structure is synchronized with the oscillatory motion of the cylinder and the interaction becomes strong. Also, it is observed that as the frequency ratio increases, the amplitudes of lift coefficient curve decrease and then increase again outside the lock-in regime. Figure 6(d) shows an increase in energy level, compared with the previous, , followed by a reduction when the frequency ratio is increased, as shown in Figure 6(e) and Figure 6(f). Consequently, this increase and decrease in the frequency peak also affect the mean drag coefficient that reaches a maximum value at (). As frequency ratio further increases, the lock-in regime no longer exists as shown in Figure 6(g) and Figure 6(h). Also, it is interesting to note that when (corresponding to the P + S mode), the smallest magnitude of the energy peak corresponds to. On the other hand, as further increases, the magnitude of tends to be constant, indicating that the large-scale Kármán vortex street has reached some stable state, corresponding to stationary condition. It is worth mentioning that is equal to the stationary case, as shown in Figure 6(h).

Figure 7 shows the time evolution of the dynamics coefficients as well as the power spectra density of the lift coefficient for. When, the drag and lift coefficients present behaviors similar to those shown in Figure 6(b). Given that each peak (both positive and negative) in the lift curve is related to the shedding of one vortex, then Figure 7(a) means that there should be eighteen vortices in the wake when the dimensionless time reaches 200. By regarding the lift curve, it is also interesting to observe a reduction in the interaction between the two frequencies, from the comparison between Figure 7(a) and Figure 6(b). In the range, from Figure 7(d) to Figure 7(f) it is verified that the amplitudes decrease when compared with the previous frequency ratio. When, the fluctuation of the lift coefficient increases again due to the change of the vortex shedding mode. For higher frequency ratios, the behavior is similar to that observed to, in such a way that the flow tends to the same vortex shedding mode as the one observed for the stationary cylinder. As oscillation amplitude increases, the lock-in regime increases () as shown in Figure 7. The amplitude peak before the lock-in regime for (), are larger than those observed in Figure 6(b) and Figure 6(c) for. As increases from to, it is observed a reduction in the magnitude

of the peak, as shown in Figure 7(b) to Figure 7(f). During the lock-in regime, the fluctuation amplitude of lift coefficient decreases, as the frequency ratio increases, and increases again outside the lock-in range. It is interesting to point out that in the lock-in regime, for the cases for which has occurred reduction in the magnitude of the energy peak, the wake structure has greater transversal space near the cylinder, while, far away from the cylinder, it decreases (see Figure 4(d) to Figure 4(f)). When, two spectral peaks can be seen again in the lift spectrum, indicating that the lock-in regime no longer exists. The energy peak associated to is greater than and its frequency value () is smaller than that of the non-oscillating case. As further increases, it can be seen in Figure 7(h) that the wake configuration tends to be the same of classical Von Kármán Street corresponding to.

Figure 8 shows the time histories of the lift and drag coefficients and the power spectra of the lift coefficient for. When, still there are “kink” on the lift curve. This kink phenomenon occurs due to the fact that as the oscillation amplitude increases, a main vortex is formed and shed on one side of the cylinder at the same time as an adjacent secondary vortex having opposite sign is formed and annihilated later by the main vortex. When, it can be observed a reduction in the amplitude of the lift curve when compared to the previous frequency ratios, and. In the frequency range (Figure 8(c) to Figure 8(g)) it is observed that as the frequency ratio increases, the fluctuation amplitude of the lift coefficient is reduced. This reduction is due to the vortex wake structure as shown from Figure 5(c) to Figure 5(g), where it was verified the 2S mode for, the elliptical wake for, and a wake with two rows of vortices near the cylinder for. At higher frequency ratios, the amplitude of the lift curves approaches to that observed for the stationary case.

For, the lock-in regime is located at the interval, for which the maximum mean drag coefficient is obtained at (). Also, as the frequency ratio increases from to, the energy level increases. After that, the energy level reduces from to. Finally, another aspect to be pointed out is that as the oscillation amplitude increases, the frequency range in which the lock-in regime occurs is enlarged: [] for; [] for and [] for.

Another relevant aspect to be investigated is the energy level of the power spectra, as shown in Figure 9. The most immediate conclusion is that as the frequency ratio increases, the energy level increases and after decreases keeping approximately unchanged for all analyzed amplitudes, for frequency ratio equal to 2. Also, higher energy levels are obtained in the lock-in regime for all amplitudes. Moreover, as the oscillating amplitude increase the energy level in the lower boundary of the lock-in regime also increase.

4.3. Comparison with other Previous Studies

It is desirable to compare the present results with some numerical results from previous studies reported by other investigators. Figure 10 (left) shows a plot of the mean drag coefficient as a function of the frequency ratio obtained for the present numerical simulations and the literature results [4] [9] , for at Reynolds number 1000. It can be noted that all the results indicate a sharp peak of the curve at low frequency ratios, and small values of at high frequencies ratio This behavior has been also observed for other Reynolds number and oscillation amplitudes [10] [23] . It can be verified that the present computational results are in good agreement with the results by references for low frequency ratios, but overestimates in high frequencies, which may reflect the assumptions of the numerical methodology used in the present calculations. It is important to mention that according to Srinivas and Fujisawa [10] , there is a great discrepancy in the literature concerning the behavior of the mean drag coefficient in the Reynolds numbers range [1000-3000].

Another aspect to be pointed out is that the maximum mean drag coefficients were obtained for the 2S mode for all the analyzed amplitudes, in which the longitudinal and transversal spacing for the oscillating cylinder is greater than those of the stationary cylinder. This fact can be observed by analyzing the vorticity contours corresponding to the maximum, as shown in Figure 11, where a is the transversal spacing and b indicates the longitudinal spacing. It should be noted that as the oscillating amplitude increases, b increases and a takes a constant value. This enables to conclude that the mean drag coefficient is more strongly dependent on the longitudinal spacing than the transversal spacing.

4.4. Pressure Distribution

The mechanism of increase and reduction of for low and high frequency ratios, respectively, can also be analyzed through the mean pressure distribution along the surface of the stationary and oscillating cylinders. Figure 12(a) shows an illustrative scheme of the angle along the surface of the immersed body, which is defined as zero at the downstream point of the cylinder.

The pressure coefficient is obtained by the relation, where is the static pressure in the Lagrangian points, is the static pressure of the undisturbed flow at the inlet of the domain, and () is the dynamic pressure taken as the reference. Figure 12(b) and Figure 12(c) show the distribution of the mean pressure coefficient for all the analyzed amplitudes and two frequency ratios. It can be noted that at the maximum local pressure () is almost unit, as expected. Also, it can be verified how the mean pressure coefficient downstream of the cylinder () varies with the cylinder oscillation amplitude. When, it can be observed that for A = 1 the mean pressure coefficient downstream of the cylinder () presents a small decrease (in absolute values) when compared with the stationary cylinder. Nevertheless, it is noted a considerable increase in the mean pressure coefficient when the oscillation amplitude increases from A = 1 to A = 2. As amplitude further increases from A = 2 to A = 3, tends to be the same for. When, it can be observed a little decrease in at for A = 1, while for A = 2, a greater reduction in value is observed from (f_r = 0.6) to (f_r = 1.5).

By comparing Figure 12(b) and Figure 12(c) for A = 3, it can be noted an inversion of the mean pressure coefficient signal, from (f_r = 0.6) to (f_r = 1.5). Thus, the forcing frequency plays an important role on the pressure distribution, enabling to verify that for low frequency ratios, the flow downstream of the cylinder is very dissipative due to viscous effects. This effect contributes to reduce the pressure and consequently to increase the drag over the cylinder. However, at high frequency ratios, the wake dynamic downstream of the cylinder is not so strong when compared to the corresponding ones obtained for low frequencies, which contribute to increase the pressure and, consequently, to reduce the drag coefficient.

5. Concluding Remarks

The numerical simulations of the flow over the rotationally-oscillating circular cylinder by using the Immersed

Boundary Method combined with the Virtual Physical Model have been addressed. Given the strong influence of the oscillation amplitude and frequency on the flow around the cylinder, the influence of these parameters on the lift and drag coefficients, on the pressure distribution, as well as on the vortex shedding frequency has been investigated.

The simulations shown that the flow structure in the near wake was strongly dependent on the oscillation frequency. Also, it observed different vortex shedding modes (“2C”, “2P”, “2S”, and “P + S”) for a fixed oscillation amplitude at different values of frequency ratios, and also for a fixed frequency ratio at different values of oscillation amplitudes, in addition to the conical wakes. Another important feature of the numerical methodology is its capability to identify the 2 C mode of the vortex shedding, which has not been observed by other investigators for the case of rotationally-oscillating cylinders.

The study reported herein enabled to observe a number of important features that should be mentioned:

・ The range of resonance increases as the oscillation amplitude increases;

・ For high frequency ratios, the wake structure configuration is similar to the classical Von Kármán Street, and the values of the vortex shedding frequency take the values corresponding to the stationary cylinder case;

・ The pressure distribution over the cylinder is influenced by forcing frequency, and consequently affects the drag over the cylinder. It implies that drag control can be done by the rotational oscillations mechanism;

・ The Immersed Boundary Method combined with the Virtual Physical Model can be easily employed in the case of moving bodies, being a very useful tool to simulate problems involving prescribed motion.

Acknowledgements

The author is grateful to the following organizations: Agency of the Ministry of Science, Technology and Innovation―CNPq for the continued support to their research work, and the Minas Gerais State Agency FAPEMIG.

Cite this paper

Alice Rosa daSilva,Aristeu daSilveira-Neto,Antônio Marcos Gonçalves deLima, (2015) Rotational Oscillation Effect on Flow Characteristics of a Circular Cylinder at Low Reynolds Number. World Journal of Mechanics,05,195-209. doi: 10.4236/wjm.2015.510019

References

NOTES

^*Corresponding author.