Received 22 May 2015; accepted 21 June 2015; published 24 June 2015

ABSTRACT

Seismic oscillations of the “building-building” system which is interconnected buildings built close to each other, and “building-stack-like structure” system which is adjacent and connected in different ways to existing building are considered in the paper. Different types of connections, such as dampers, including the ones suggested by the authors, are studied. Seismic impact is given as a harmonic function and various existing accelerograms, including synthesized ones. Distinctive feature of this paper from previously published ones [1] [2] is the fact that the emphasis falls on the influence of soil-foundation interaction properties, which are described using various models of load-displacement connections. Calculation results are compared in the case of representation of the building as concentrated masses and spatial systems. Ways to reduce seismic response of buildings during the earthquakes are pointed out. Results of experimental studies are given in the paper and are compared with calculations.

Keywords:

Interaction Properties of Soil-Foundation, The Rigid Foundation, Kelvin-Voigt and Maxwell Models, Damper, the Coulomb’s Force, Modeling, Similarity Multipliers, Dynamic Characteristics, Oscillations, Sensors, Accelerogram, Absorption Factor

1. Introduction

The difficulty to predict where, when and with what magnitude an earthquake will strike leads to the strengthening of the necessity to build earthquake-resistant buildings and structures and to develop seismic engineering. One of the ways to improve earthquake resistance of buildings is to provide constructive solutions, which absorb seismic energy. Usually, such solutions are carried out in the process of design, calculations and construction of buildings. Efficient use of land resources in modern construction and an expansion of cities nowadays lead to a trend to construct adjacent buildings―close to each other.

In addition, there is a tendency to expand the living space, building an attachment in the form of stack units to the main building. Stack-like structures of different height may be observed in the reconstruction of a number of administrative buildings. Connections of “building-building” system are usually carried out using various types of oscillations dampers. As for the system “building-stack”, the parts may be connected rigidly or with dampers. Structures of connecting elements are numerous; some of them are given in [3] [4] .

The study of oscillations of the buildings, connected with different types of dampers, is presented in the papers [5] [6] . They give results of calculations, and define dynamic characteristics of adjacent buildings and standing apart ones. In these works, the foundation is considered to be rigidly fixed in soil.

2. Statement of the Problem

It is assumed, that the building has an n floors. Under seismic effect it oscillates in a plane of the least rigidity, i.e. it oscillates in horizontal transverse direction only. At the beginning, the building is modeled by adopted design scheme in the form of a console with concentrated masses on the floors. Viscous-elastic characteristics of the building itself, and foundation displacement relative to soil are considered here. Both buildings (Figure 1) in the “building-building” system, interconnected on floor levels with dampers are subjected to shear waves, and in the “building-stack” system the building is subjected to shear vibrations and the stack?to bending ones.

Oscillation equation of the system “building-building” is written in the following form [7] :

(1)

And for the system “building-stack” equation of stack oscillations is written in the form [8] :

(2)

where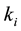, are floor rigidities on shear;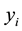, 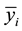are floor deflections;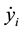, are floor velocities;, 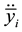are floor accelerations;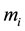, 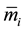are floor masses; δ_ij is floor displacements from unit force;, are floor viscosity coefficients.

In (1) and (2), R(y₀) is a force of the effect between foundation and soil; it may be written in different ways. When this connection obeys to elastic law, it has the following form:

(3)

where is foundation-soil interaction coefficient; is foundation displacement relative to soil.

When load-displacement connection obeys to elastic-plastic law, it has the form [9] :

(4)

where is some experimental function, which characterizes non-linear properties of interaction. The form and the value of the function obtained experimentally at foundation shear relative to soil, are presented in [10] .

Besides, the force R on the basis of hereditary theory of viscous-elasticity may be taken also in the form [11] :

(5)

Here is a relaxation function.

Calculation results, obtained when viscous-elastic properties of interaction are taken according to Kelvin- Voigt model, are given in the paper:

(6)

or according to Maxwell model

(7)

here is a constant called relaxation time; E is elasticity modulus of material; K is viscosity coefficient or coefficient of internal resistance to element strain.

Writing (t―tangential stress in foundation-soil contact; S―contact area) and giving foundation displacement relative to soil in the form, after some computation we will get:

(8)

where ; and are symbols at transformation, is coefficient of soil damping; is circular frequency.

When solving Equations (1) and (2), the forces of response of connecting element (damper) are added to inertia forces for the first building with positive sign, for the second―with opposite one.

It is supposed that the buildings are interconnected with oscillations damper [12] , its structure shown in Figure 2. It consists of ferroconcrete column base 1, sand 2, compensator of steel sheet 3, reinforcement as an elastic connection 4 and steel plates 5. In the base of this structure lays the damper, offered by Klgatyan [13] .

Here, response forces of connecting element are written in the following form:

(9)

where с is a rigidity of elastic element; µ is viscosity coefficient of a damper; F_k is Coulomb’s force, which (between the plate and sand) is written in the form:

(10)

here n is a number of plates; f is coefficient of dry friction of sand with steel;, are displacements of the

left and right ends of compensator, respectively; ℓ₀ is a length of compensator; E is deformation modulus of sand; is plate area; is unit vector, which points the direction of system motion; α is an angle of plate

inclination. The structure of connecting element (Figure 2) allows us to select the most rational value of the force F_к for the system “building-stack” by varying a number of plates n and an angle of its inclination α.

3. Experimental Studies of the System “Building-Building” and “Building-Stack-Like Structure” under Micro-Seismic Effects

It is known that field experiments require vast capital investments. Besides, it is almost impossible to conduct twin-tests in field conditions. Therefore, to solve this problem the tests have been conducted with the models using the principles of physical simulation, which are described in details in [14] . The most acceptable principle for the solution of this problem is a simple similarity [15] . In modeling we may use the same material as in field conditions. In this case if field condition presents heavy concrete of high grade, for the model we may take light concrete of low grade. The aim of the experiment is to determine dynamic characteristics of the building, assuming that strains are elastic ones only. So material of a framework may not be modeled. To solve this problem a section of four-storey large-panel building with attached stack-like structure has been modeled (Figure 3).

The processes of static and dynamic strain of rigid bodies are characterized by the following values: linear dimension ℓ, stress σ, relative strain ε, material density ρ and time t. Conditions between field experiments and a model depend on their material.

In this work the scale of modeling (similarity factor) ia taken as equal to α = 1/5. To prevent cantledge of the model (to compensate the lack of volume forces) accelerations of full-scale experiment and a model are taken as similar ones.

Strength characteristics of field structure and a model, taken for the material of field structure and calculated for a model, are presented in Table 1, where R is a cubic strength of concrete; R_pr is prism strength of concrete; E₀ is elasticity modulus of concrete; R_a is yield strength of a reinforcement; E_a is elasticity modulus of a reinforcement; asterisk refers to a model.

Design similarity factors of discussed structure for these values are (Table 2).

In fabrication of structure elements of the section of large-panel building, steel annealed rods with respective diameters have been used as reinforcement. Their yield stress and elastic modulus, obtained from laboratory test results are 16% and 22% different from design values, as shown in Table 1. It is assumed that these differences effect insignificantly on dynamic characteristics of the building. Expanded-clay concrete was taken as a light concrete. Brand of cement in concrete mortar is 400 M, and it is added to a mortar according to concrete grade.

Figure 4 shows the model of building section А and the model of attached stack В.

Physical-mechanical properties of soil are the following: density −16.7 kN/m³; porosity coefficient −0.595; an angle of internal friction −29.1˚; cohesion coefficient −21.4 kPa; strain modulus −9.6 MPa.

During the tests dynamic characteristics of the model of the building and the stack have been determined separately and then connected with offered damper. Oscillations of the model of the building have been carried out by two ways: by tension with wire and weight dropping. During the tests, accelerations in different points along the height of the building and the stack have been recorded.

Oscillations have been recorded by DYTRON (USA) detecting elements (sensors) with piezoelectric elements. The sensors have been manufactured to record the signals of one or three components. The signals in the form of stresses via convertor enter the computer. Computer software transforms stress signals into accelerations. The sensors may be adjusted to different frequency ranges. During the tests the computer was adjusted to the frequencies most often observed under micro-seismic oscillations.

Experimental results have been translated to full-scale buildings, using the scale of modeling and built spectral densities of “Matlab” program. Before starting serial experiment, preliminary experiments have been conducted, where all floors (except the first) have been connected by connecting elements in different combinations of them. These preliminary experiments have shown that the greatest effect is achieved when connecting the third and the fourth floors by viscous-elastic coupling. Below are the results of experiments when only the third and the fourth floors are connected by connecting element of “building-stack” system.

According to accelerations records and built spectral densities, floor displacements of “building-stack” system, connected by proposed connecting element have been determined. For this purpose, the graphs have been built, based on calculated values of maximal amplitudes of oscillations, of dependences of displacements of standing apart building and stack-like structure, and after their connection, that is, “building-stack” system, schematized in the form of a cantilever beam with concentrated masses (Figure 1).

4. Results of Calculations and Experimental Investigations and Their Analysis

Seismic effect in calculations have been given in the form of damping sinusoid:

(11)

Accepted parameters of these effects are the following: amplitude of soil oscillation А = 0.15 m; damping ratio α = 0.15; period of oscillation Т = 0.5 s; w = 2π/T.

Calculations have been carried out to the effect of accelerogram, taken in the form of synthesized accelero- gram СА-482, which generalizes the properties of all types of accelerograms, in particular, of low frequency (Bucharest, 1977), high frequency (Gazli, 1976) and mid-frequency (El-Centro, 1940) earthquakes. This accele- rogram has been digitized by the step 0.005 s, with duration 4.3 s.

Floor masses and rigidities are taken as the ones of 4-storey large-panel building of 76-017СА/53 series.

Calculated parameters of existing building based on project data are the following: m₁ = 258; m₂=213; m₃ = 213; m₄ = 213; m₅ = 190; (10³ N×s²/m); k₁ = 35.04 ´ 10⁶; k₂ = 26.846 ´ 10⁶; k₃ = 26.846 ´ 10⁶; k₄ = 26.846 ´ 10⁶; k₅ = 26.846 ´ 10⁶ (10³ N/m).

The ones accepted by design data for a stack-like structure are;;;; (10³ N×s²/m);;;;;;;; ;;;; ;;; (10⁻³ m/N).

With account of floor resistance force, resistance coefficient has been determined by the following expression:

(12)

where? is absorption coefficient, for practical use taken as equal to 0.6 [16] .

Figure 5 and Figure 6 show deflections of the buildings considered as a console beam with concentrated masses on the floors (A) and as a spatial system (B). In these calculations the foundation is considered to be rigidly fixed in soil, and seismic effect is taken in the form (11). Floor viscosity has been neglected. As seen from Figure 5 and Figure 6, the difference in deflection values is null, except for middle floors. Similar conclusions may be drawn from results of calculations of 9-storey and 16-storey buildings (Figure 6). Based on above mentioned, calculation results by console scheme only are presented (floor viscosity is taken into consideration in all cases).

To compare experiment results with design data on displacements values from Building Code [17] seismic forces (shear forces and bending moments), generated on the floor, have been determined. Results of experiments and calculations have shown that the most effective is the connection of a buildings and a stack by connecting element, having two plates. Below we compare the results obtained from experiments and calculations. Figure 7 shows the results of experiments to determine the displacements in “building-stack” system; Figure 8 shows results of calculations. Comparison of Figure 7 and Figure 8 shows that the displacements of upper floor of a building and a stack differ on 59% and 48%, respectively. In experiments displacements values are greater. This can be explained by the following. Calculations take into account real rigidity of the building. It is known that in construction of large-panel buildings, butt joints of the panels and floor slabs after welding are filled with concrete. This increases the rigidity of the whole building. In manufacturing the model of the building their panels and floor slabs have been welded together, but to fill them with concrete appeared impossible. Therefore, it was impossible to achieve the rigidity of the model corresponding to the one of a full-scale building. To our opinion this is the cause of significant differences of experimental and calculated data. In addition, this difference is also affected

by the properties of material used and the technology of model construction. Nevertheless, the above factors (shortcomings) have not effected significantly on the goal achievement, because the experiments before connecting the building with a stack and after their connection have been conducted under identical conditions.

The difference of test data from calculated ones after connection of the building with a stack-like structure with a damper on the upper floor is 15% for a building and 36% for a stack. In tests the damper reduces building displacement to 47%, and stack displacement to 83%. Similar conclusions may be drawn for lower floors.

The use of proposed connecting element in the system “building-stack” reduces force factors (shear forces and bending moments), according to tests and calculation data.

A design for the first case has been conducted to compare displacements and force factors occurring at rigid connection of the building and stack-like structure with a damper. The building and stack-like structures are considered as a single system. In determining the displacements it was assumed that the system performs shear oscillations only. A comparison of numerical results shows that the displacement at rigid connection is 16% greater, than at “building-stack” connection. Load on the building at rigid connection is 3% less, and with the use of a damper it is reduced by 12%. Therefore, it can be stated that the connection of “building-stack” system with a damper increases seismic stability of the building by 15%, as compared to rigid connection.

The use of proposed connecting element gives a good result at stack-like structure attachment to a building of less rigidity (such as brick ones) than the large-panel ones. The decrease in the deflection at the upper floor is 66% and at the lower floor-51%. However, the deflection of the upper and lower floors of stack-like structure shows more than 2 times rise. This increase slightly effects on “building-stack” displacement on the whole.

Figure 9(a) and Figure 9(b) show calculation results with the model of soil-foundation rigid connection, elastic (3), visco-elastic Kelvin-Voigt (4) and Maxwell models (5). In these calculations К = 4 * 10⁷ N/m³ and h

= 0.152 * 10⁵ Ns/m² are taken; they corresponds to loamy soil. The character of soil-foundation interaction has no practical effect on displacement of a standing apart building and stack-like structure. The influence of this factor when connecting them with a damper is significant. Depending on accepted model the values of building displacements are reduced to 54%, and stack-like structure-to 3%. Similar calculations have been conducted at К = 3 * 10⁷ N/m³ and h = 0.32 * 10⁵ N s/m² and К = 5 * 10⁷ N/m³ and h = 0.78 * 10⁵ N s/m², they correspond to sand and loess, respectively. Conclusions made on the basis of these calculation results are practically the same as the ones for loamy soil.

Calculations have also been performed at altering К or h, ceteris paribus (Figure 10 and Figure 11). With ac-

cepted in calculations values of К its alteration from 0.5 to 5 (10⁷ Н/m³) at constant value of h effects insignificantly on deflections of the building before and after its connection with stack-like structure with a damper. This conclusion is valid for any accepted model of soil-foundation interaction, except for Maxwell model. The increase of h in any case decreases the values of deflection both before connecting with a damper and after it. Calculations (of 9 and 16-storey buildings) show that the higher the building, the greater is the effect of foundation yielding.

5. Conclusions

Ø Calculations show that the deflections in calculation of the building as a bar with concentrated masses on the floors and as a spatial box are practically the same, except for middle floors, where the difference is insignificant (5% - 6%). This conclusion is also applied to buildings interconnected by means of dampers.

Ø Connection of buildings with dampers on all floors is optional; it is sufficient to connect them in two places along the height: at a height (0.35 ÷ 0.4) h and (0.6 ÷ 0.7) h (h is a total height of the building).

Ø Accepted models of soil-foundation interaction affect slightly buildings of low height. This effect increases with the height of the building.

Ø The effect of the dampers is greater when brick building (less rigid) is attached to stack-like structure (more rigid).

References