Received 19 March 2014; revised 18 April 2014; accepted 16 May 2014

ABSTRACT

The purpose of this study was to further develop the constant power model of a previous study and to provide the final solution of Hill’s force-velocity equation. Forearm and whole arm rotations of three different subjects were performed downwards (elbow and shoulder extension) and upwards (elbow and shoulder flexion) with maximum velocity. These arm rotations were recorded with a special camera system and the theoretically derived model of constant maximum power was fitted to the experimentally measured data. The moment of inertia of the arm sectors was calculated using immersion technique for determining accurate values of friction coefficients of elbow and whole arm rotations. The experiments of the present study verified the conclusions of a previous study in which theoretically derived equation with constant maximum power was in agreement with experimentally measured results. The results of the present study were compared with the mechanics of Hill’s model and a further development of Hill’s force-velocity relationship was derived: Hill’s model was transformed into a constant maximum power model consisting of three different components of power. It was concluded that there are three different states of motion: 1) the state of low speed, maximal acceleration without external load which applies to the hypothesis of constant moment; 2) the state of high speed, maximal power without external load which applies to the hypothesis of constant power and 3) the state of maximal power with external load which applies to Hill’s equation. This is a new approach to Hill’s equation.

Keywords:

Arm Movement, Force-Velocity Relationship, Muscle Power, Hill’s Equation

1. Introduction

Hill’s force-velocity relationship of skeletal muscle (Figure 1) [1] [2] is one of the most essential equations of

muscle mechanics and it has been an object of biomechanical studies for years (e.g., [3] - [6] ). In muscle me-

chanics, this relationship is often presented by Hill’s equation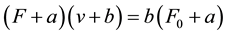, where F is current muscle force at current shortening velocity of contraction, a is constant force and b is constant velocity, F₀ is the maximum isometric muscle force, i.e., the maximum force that muscle can develop at a given constant length, and v is velocity [1] [2] . For comparison between different muscles b is best expressed in terms of b/l₀, where l₀ is the standard length of muscle. This equation was based on laboratory measurements with a Levin-Wyman ergometer in which the activated muscle was released at a suitable speed in an isolated muscle condition. The obtained constant velocity was then plotted against the observed tension. Force measured from skeletal muscle during maximum tension depends on several internal and external factors which have been thoroughly reviewed (e.g., [3] [7] [8] ). Matsumoto [9] mentioned that because almost all the isotonic data have been restricted to one muscle length l₀, the maximum length with almost no resting tension, and the velocities measured are those initial values when the load begins to move. Examining the length region, l £ l₀, for an isotonically contracting muscle, Matsumoto [9] found that the constants a/F₀ and b/l₀ remained fixed throughout the range of lengths over which the shortening takes place. In contrast to Hill’s isolated muscle preparations, force (F) of the involved muscles in rotational movement creates a moment (M = r ´ F) about the joint. The length of the muscle’s moment arm (r) changes as the rotational movement proceeds about the joint axis. This rotation movement is the combined effect of the forces of several different muscles. However, it is difficult to determine the contribution of each muscle on force production due to many different factors, and also to determine the torque about the joint. Several extensor and flexor muscles were used by Raikova [10] in her model of the flexion-extension motion in the elbow joint. Furthermore, the force of a skeletal muscle is an accumulation of forces generated by active motor units belonging to this muscle [11] . Raikova et al. [12] mentioned that access to each motor unit (MU) is impossible, and the recruitment and force developing properties of all individual MUs cannot be known. In this paper [12] the process of learning fast elbow flexion in the horizontal plane was simulated and the result was compared with experimentally measured data.

Previous experiments of Rahikainen et al. [13] were based on the theory of arm rotations including four phases: 1) start of the motion; 2) phase of constant maximum rotational moment; 3) phase of constant maximum muscular power; 4) stopping of the motion. It was assumed that the muscular system is able to transfer only a certain amount of chemical energy during the time of contraction and therefore, arm rotation must have maxi- mum power that cannot be exceeded. It was also assumed that the maximum power acts within a certain range of velocity which was considered as constant maximum power and this is possible only when the velocity is high enough. The velocity of the motion increases to the point where the maximum power occurs and acting rotational moment is less than the maximum moment. Consequently, power remains constant as the angular velocity increases and the moment decreases.

The present study continues the experiments of Rahikainen et al. [13] and further develops its theory of mechanics. The previous study presented a constant power model and its validity and accuracy of results were assessed. In the present study new arm rotation experiments of three subjects were captured with two different re- cording systems. More accurate calculations of moments of inertia and a new more effective determination of the matched range of measured and theoretical angular velocity curves were used. Also a new approach to Hill’s equation was presented. In the left side of Hill’s equation 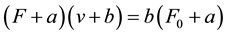the constant a has the dimensions of force and b the dimensions of velocity, otherwise addition is impossible. Therefore, (F + a) is force and (v + b) is velocity, and force multiplied by velocity is power as can be seen in Figure 1. The term (F + a) (v + b) is muscles’ total power including Fv, which is the power of moving the external load. The right side of the equation, b (F₀ + a), includes only constants in this regard the equation can be considered as a constant power model. However, the constant power of Hill’s equation presented in this paper is not the above mentioned power of Hill’s original curve as it is usually considered in biomechanics, but it is the sum of three different power components (see Discussion and Conclusions). The constant power model of this study acts during high speed movements with no external load, where Hill’s equation does not seem to fit the experimental points ( [2] p. 32, Figure 3) very well. As an explanation for this mismatch Hill mentioned that “sharp rise at the end of the curve in the region of very low tension was due to the presence of a limited number of fibers of high intrinsic speed and no such equation could fit the observed points below P/P₀ = 0.05”. The present model is based on the muscular system’s ability to transfer chemical energy and, therefore, it is not necessary to know the contribution of the individual muscles involved.

The purpose of the present study was to examine how the theoretical constant power model which was first used in linear motion [14] and later applied to rotational motion [13] fits the measured angular velocity curves of arm rotation experiments. The further purpose of the study was to determine how Hill’s equation functions as a constant power model and to compare Hill’s equation with the model of the present study.

2. Materials and Methods

In the present study, the measurements of arm rotations (Subjects S1 and S2) were recorded by a special camera system [15] [16] . Figure 2 shows the principle of the system where angular velocity was calculated with the Formula:

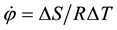(1)

where R is arm length, ΔS is the distance between two successive measuring points and ∆T is time increment. Additional elbow flexion and extensions were performed for one Subject S3 by using Vicon motion analysis system with 8 cameras. This system made it possible to use higher frame rates (300 Hz). Subjects were normal healthy people representing different age and physical activity background (S1: 62 years, 1.80 m, 82 kg; S2: 35 years, 1.69 m, 73 kg, aikido training, weight lifting and S3: 25 years, 1.83 m, 70 kg, high jumping).

The accuracy of the special camera system has been described in references [13] [15] - [17] . The angular velocity-time curves were drawn (with a line thickness of 0.5 mm) on the squared paper, where 1 mm corresponded to an angular velocity of 0.1 rad/s and time of 1 ms giving the accuracy of velocity curves. The theoretical and measured angular velocity curves coincided within the distances of 35 - 70 mm, which was enough for the verification of the constant power model in the arm rotation experiments. Slight oscillations at the beginning of the movement did not exist within the constant power phase and, therefore, the verification of the constant power model was possible in all experiments. The accuracy of the Vicon recording device, verified by calculating the root-mean-square error for each camera, ranged from 0.06 to 0.17 mm during calibration.

2.1. Model of Arm Rotation

The model used in the present study is constructed according to Newton’s II law and it was first used in linear motion [14] and then applied to rotational motion [13] by Rahikainen et al. The theory of arm rotation is as follows: At the beginning of the movement, angular velocity is naturally zero and it takes some time to generate force. At this early phase of motion, elastic properties of muscle-tendon complex has influence on the motion, but at the state of full tension, these elastic elements have no further dynamic effect. Thereafter it can be

assumed that a maximum muscle force takes action and within rotational motion maximum rotational moment acts as well. At this phase of motion there is a constant value of glide friction acting. Because the muscle system is able to transfer only a certain quantity of chemical energy during the time of contraction, there must be a constant maximum power, which the muscle is able to generate within a certain range of velocity. As the velocity increases the motion reaches the point where the maximum power takes action and acting rotational moment is less than the maximum moment. This way power remains constant as the angular velocity increases and moment decreases. Now, liquid friction, directly proportional to velocity, is acting. The constant glide friction decreases as forces at the joint decrease and it becomes negligible. During the constant power phase of the model rotation- al moment is moment of inertia multiplied by angular acceleration which equals the moment generated by muscle force minus the moment generated by inner friction of muscle. The effect of gravitational force is added afterwards (see Paragraph 2.3). The model of arm rotation is the equation of motion:

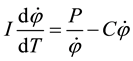(2)

where

Moment of inertia in arm rotation I

Angular velocity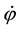

Power generated by arm muscles P

Time T

Moment generated by muscle force

Moment generated by inner friction of muscle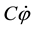

Coefficient of friction C

Inner friction of muscle is liquid friction inside muscle, which is directly proportional to velocity. The same liquid friction was also used in the study of Rahikainen et al. [17] which was initially adopted from Alonso and Finn [18] . It was assumed that, initially, movement proceeds at a constant maximum moment and then moment generated by the muscle force (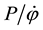in Equation 2) is constant. It was also assumed that, as velocity increases, movement proceeds at constant maximum power at a certain range of velocity and then the power P in Equation 2 is constant. In order to determine the validity of this hypothesis, Equation 2 was solved for angular velocity-time function and this equation was employed for validity determination.

The solution of Equation 2 from the previous study [13] :

(3)

2.2. Calculation of Moment of Inertia

The mass distribution of the subject’s arm sectors differed from the average values of mass tables in the literature. Therefore, the mass distribution of the arm sectors were determined by sinking the arm sectors into water. The masses of the arm sectors were calculated by multiplying the over flowed water volume with the corresponding arm sector density. The length of the subject’s whole arm was measured with fist clenched, and the lengths of arm sectors (hand, forearm and upper arm) were measured. According to Winter [6] the arm sector densities (kg/l) were as follows: hand 1.16, forearm 1.13, upper arm 1.07.

Definition of moment of inertia:

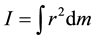(4)

where dm is rotating mass and r is the distance of rotating mass from the rotational axis. Derivation of the moment of inertia about the end of arm sector assuming even mass distribution:

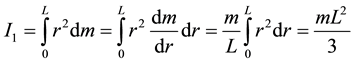(5)

where m is the mass of rotating arm, and L is the length of rotating arm. Derivation of the moment of inertia about the center of the arm sector assuming even mass distribution:

(6)

Because the distribution of mass in the arm sector is not even, the moment of inertia of an additional mass was calculated with Formula:

(7)

where m is additional mass of the arm sector and r is the estimated distance of the center of gravity of additional mass from the rotation axis. Subjects’ arm sector distances, lengths and masses are presented in Table 1. These values are then substituted in the above mentioned Equations 4-7 to calculate the final moments of inertia of forearm and whole arm rotations about the elbow and shoulder joint (example for S1 summarized in Table 2).

Moment of inertia of forearm rotation

Forearm

Moment of inertia of major forearm mass about the elbow joint (m = 1.0 kg, L = 0.28 m):

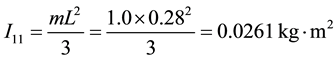
Moment of inertia of additional forearm mass about the elbow joint (m = 0.24 kg, r = 0.07 m):

Hand

Moment of inertia of the hand sector about the center of mass (m = 0.58 kg, L = 0.11 m):

Moment of inertia of the hand sector about the elbow joint (m = 0.58 kg, r = 0.34 m):

Light marker battery

Moment of inertia of the battery about the elbow joint (m = 0.26 kg, r = 0.37 m):

Total moment of inertia of forearm rotation about elbow joint

Moment of inertia of whole arm rotation

Upper arm

Moment of inertia about the shoulder joint (m = 2.14 kg, L = 0.30 m):

Forearm

Moment of inertia of the major forearm mass about the center of mass (m = 1.0 kg, L = 0.28 m):

Moment of inertia about the shoulder joint (m = 1.0 kg, r = 0.44 m):

Moment of inertia of additional mass about the shoulder joint (m = 0.24 kg, r = 0.37 m):

Hand

Moment of inertia of the hand sector about the center of mass (m = 0.58, L = 0.11 m):

Moment of inertia of the hand sector about the shoulder joint (m = 0.58 kg, r = 0.64 m):

Light marker battery

Moment of inertia of the battery about the shoulder joint (m = 0.26 kg, r = 0.67 m):

Total moment of inertia at whole arm rotation about shoulder joint

According to the above mentioned calculations, the corresponding moments of inertia of forearm rotation and whole arm rotation for S2 were 0.110 and 0.551 kg×m², respectively. As the total length of forearm and hand was the same for Subjects S1 and S3, it was assumed that the moments of inertia of these segments were also the same and, therefore, the moment of inertia of forearm rotation about the elbow joint for S3 was 0.131 kg×m². The measurements with Vicon camera system for S3 were done with reflective markers and the corresponding moment of inertia without the battery was 0.095 kg×m².

2.3. Effect of Gravitational Force on the Movement

In forearm rotation, the effect of gravitational force is minor compared with maximum muscle forces and the moment induced by gravity was omitted from the motion model (Equation 2). In whole arm rotation, this moment is added to the motion mechanics in the following manner: The power generated by this gravitational moment is, where mg is gravitational force of arm segments, r is distance of the center of gravity of segments from the rotation axis and angular velocity of arm rotation. The theoretical angular velocity (Equation 3) and the measured angular velocity match within a very narrow velocity range and the power induced by gravity can be calculated as a constant factor. It is included in the power P ac- cording to the previous study [13] .

2.4. Determining the Matched Range of Measured and Theoretical Angular Velocity Curves

Figure 3 shows the technique that was used to determine the matched range of measured and theoretical angular

velocity curves. Friction coefficient values (C) and power values (P) were obtained by fitting the theoretical angular velocity curves to the measured ones. These two curves coincide only if certain C and P values are used in the fitting process. The measured angular velocity values are shown as points on the velocity curve and the theoretical angular velocity (Equation 3) is shown as a broken line. The matched range was found by using the following iteration procedure: based on previous experiments, the randomized initial values (see Figure 3) within the matched range were selected for angular velocity at point 1. A zero point on the time axis for the theoretical angular velocity was selected 0.050 s before point 1, which corresponds to 0.060 s on the time axis of the figure. Thereafter, the direction of iteration process was observed and after some iteration, the final theoretical angular velocity was drawn according to Equation 3 to match the measured velocity curve. The correct theoretical angular velocity was obtained with the zero point at 0.073 s on the time axis. The ratio of power and friction coefficient in Figure 3 is

(8)

The final theoretical angular velocity was drawn with moment of inertia I = 0.135 kg×m², friction coefficient value C = 2.92 kg×m²/s and ratio of power and friction coefficient P/C = 354 1/s².

3. Results

Arm rotation experiments recorded by the camera system of Rahikainen [16] are presented in Figures 4-7 and experiments with Vicon motion analysis system in Figure 8. The theoretical angular velocity curves in Figures 4-8 are marked with broken lines and they coincide with the measured angular velocity curves (solid lines) between the points A - B, where movement proceeds at constant power. Initially, movement proceeds at constant acceleration, then liquid friction becomes influential and acceleration decreases just before the section A - B (constant power), which is finally followed by stopping of the movement. In general, the sections A - B are long enough to verify the existence of the constant power model. The measurements in Figure 8 with Subject S3, made by the Vicon motion analysis system, did not have a clear section of constant acceleration at the beginning of the movement. High oscillation in that section turned it indefinite. In the elbow extension, the oscillation is weak and the usual constant acceleration section can be distinguished at the movement initiation. It also seems that the constant acceleration section in Figure 6 has a similar oscillation as in Figure 8.

The measured data in Figures 4-8 have been smoothed by the 6^th order polynomial curve fitting. The used friction coefficient values varied between 2.8 - 3.1 kg×m²/s in forearm rotations and between 3.6 - 3.8 kg×m²/s in

whole arm rotations. The maximum angular velocities ranged from 13.7 rad/s (shoulder flexion) to 24.8 rad/s (elbow extension). The effect of the ratio of power and friction coefficient P/C on the progress of angular velocity is clearly seen in Figures 4-8. In Figure 4, the typical variation in consecutive trials of the same subject is seen. The effect of gravity can be seen in Figure 6 and Figure 7 as the shoulder extension has larger rotating angular velocity than the shoulder flexion.

4. Discussion and Conclusions

The present study confirmed the existence of constant power model in arm rotations with maximum velocity. The theoretical and measured angular velocity curves showed a short range of coincidence because the arm rotations were made at maximum velocity, but the range was long enough to verify the model. If there were a constant force resisting the arm rotation, the speed of motion would be slower and the velocity-time curve of measured arm rotation would follow the theoretical constant power curve (broken line, Figures 4-8) levelling horizontally as time proceeds. Thus a constant force in arm rotation movement corresponds to a constant velocity in the same manner as a force corresponds to a velocity in Hill’s equation.

After the initiation of arm rotation, the movement proceeds at a state of low speed, high acceleration without external load. In this phase of movement it is assumed (hypothesis) that the movement proceeds at a constant maximum muscular moment. Measurements of the rotational movements show that movement proceeds at constant angular acceleration. Therefore, we can conclude that the torque accelerating the movement, or the right side of Equation 2, is constant.

Torque generated by the maximum muscular moment is and according to the hypothesis it is constant. The moment generated by frictional force is not constant (because of the term of velocity) and, therefore, this hypothesis is not fulfilled. However, the finding “movement proceeds at constant acceleration” is interesting and should be studied more closely. In Equation 2 kinetic friction was assumed to be directly proportional to velocity at the beginning of the movement. This is a new hypothesis which is not necessarily true. It is possible that kinetic friction at small velocities is constant and at high velocities is directly proportional to velocity. This leads to a constant torque accelerating the movement at the beginning of movement.

After the phase of constant angular acceleration the movement proceeds at high speed and low acceleration without external load. It is assumed that, within this phase, the movement proceeds at constant maximum muscular power. This hypothesis seems to be true between A and B in Figures 4-8. This is the most interesting finding of the present study and further development of Hill’s equation provided another kind of model of constant power.

Final solution of Hill’s force-velocity equation

The experiments of the present study verified the conclusions of a previous study [13] in which theoretically derived equation with constant maximum power was in agreement with experimentally measured results. As Hill’s equation is also a constant power model it can be considered the same as the model of this study in that respect. Hill’s force-velocity relationship was created by experiments in which the velocity of muscle contraction was measured against a certain constant force. The experiments of Hill’s equation naturally started at zero velocity and continued in the same manner as the experiments of the present study through all the phases. Be- cause of the external load, the experiments of Hill’s equation did have slower velocities and, therefore, it was possible to reach maximum velocity within the measuring accuracy. The measurements of the present study were made without external load and none of them reached the maximum theoretical velocity of Equation 3.

The results of Hill’s experiments could be transformed into hyperbola equation describing force-velocity dependence of the movement. Figure 9 represents a further development of Hill’s force-velocity relationship. The

Force-velocity axes are shown and also the asymptotes have been drawn as broken lines. Hill’s equation, (F + a) (v + b) = constant, implies that the area of the rectangle (F + a) (v + b) is constant. The total power of the muscle is comprised of three different components represented by rectangles A, B and C. The area of rectangle A = F v represents the power needed from muscle against an external load (see the power curve in Figure 1). If there is no external load, this power is consumed by acceleration. The area of rectangle B = (F + a) b represents the power of muscle’s internal loss of energy. This power creates a counter force against an external load. As the velocity is zero, this power B is highest and, therefore, it is not related to external movement. Thereafter, as velocity increases, this power decreases rapidly initially, then slowly at higher velocities. The area of rectangle C = va represents the power of friction due to the motion of the muscle-load system. Because power is the force multiplied by velocity, the force of friction is a. This is not force directly proportional to velocity, generally known as liquid friction (which is the friction used in the present study), but constant force of friction which is known as glide friction. Now we can see that there are three different states of motion: 1) at the beginning of motion characterized by a state of low speed maximal acceleration without external load; then 2) as the motion continues a state of high speed, maximal power without external load and 3) a state of maximal power with external load, which applies to Hill’s equation. The maximum power is due to the fact that the transfer of energy within the muscle system must have a maximum rate and, therefore, muscle’s power generation must also have a certain maximum rate. Within Hill’s equation maximum power is due to the ability to lift loads and within experiments of the present study due to the high speed of motion.

Muscle mechanics of the present study are based on the experiments which were performed with maximum velocity and therefore the constant power phase became short. If there is a constant force resisting the motion, the motion becomes slower and it can be inferred that the time-velocity curve levels horizontally at the velocity of Hill’s equation. Another kind of mechanics applies if less muscle force is used and the traditional Hill equation applies to movements that are resisted by external force. From the results of the present study it can be seen how these states of motion relate to each other and the findings enable further development of muscle mechanics in this field of modern science. The calculation methods of this study can be applied in research areas of sports and medicine.

References